软钢阻尼器对建筑楼层反应谱的影响
2020-01-14蒲武川张华珺
蒲武川,徐 熙,张华珺
(武汉理工大学土木工程与建筑学院,湖北武汉 430070)
0 引 言
非结构构件是建筑物重要组成部分,主要包括维护结构、专用设备、室内家具等。地震中,非结构构件的破坏和脱落可直接导致人员伤亡,而且非结构构件失效会直接产生高额的经济损失,研究表明地震造成的非结构构件相关的经济损失可达总建筑造价的75%~85%[1]。非结构构件破坏导致的建筑功能降低或失效对结构震后功能的恢复产生严重影响。因此,对非结构构件的地震响应进行准确的评估并对其响应进行合理的控制非常重要[2]。非结构构件涵盖范围较广,根据其与主体结构的连接方式及自身动力特性,主体结构的变形和加速度都可对其形成加载。在验算加速度敏感型设备与主体结构的连接件性能时,通常采用楼层反应谱(Floor Response Spectra,FRS)进行评估[3]。FRS与地震反应谱概念类似,它描述了具有不同自振周期的非结构构件在楼面加速度激励下的最大加速度响应。FRS的大小依赖于非结构构件和主体结构的动力特性以及相互之间的关系。
要评估非结构构件的加速度响应,可采用精确的时程分析方法,或者采用近似的直接估计方法,FRS相关的研究更多地集中于后者。楼层反应谱早期多应用于核电站工业厂房中[4]。1997年,Villaverde[5]总结了当时与非结构构件相关的抗震设计理论和试验研究成果,并提出了未来研究的发展需求,包括考虑结构非线性行为、扭转效应的简化分析方法,以及基础隔震和结构控制技术在非结构构件中的应用。Yasui等[6]提出针对弹性结构的FRS直接估计方法,通过理论推导得到非结构构件的加速度响应,将非结构构件的最大加速度响应由直接受到地震动作用下主体结构和非结构构件的最大加速度近似表示。秦权等[7-8]在20世纪90年代基于随机振动方法开发了楼层反应谱的计算程序。2003年,Paskalov等[9]基于随机振动理论,提出了针对复杂结构的FRS估计方法,为FRS直接估计方法研究提供了新思路。苏经宇等[10]从主体结构和非结构构件动力特征联系的角度提出了确定楼层反应谱的简化方法。
对弹塑性结构系统,很多研究人员也开展了FRS的特征及评估方法研究。Medina等[11-12]对非线性结构进行了时程分析,指出结构的非线性行为能够降低FRS,并提出了修正系数来拟合结构非线性引起的响应降低率。Oropeza等[13]研究了主体结构和非结构构件自振频率、强度折减系数以及滞回模型(弹塑性模型、γ-模型、修正的武田模型以及Q-模型)对FRS的影响。Vukobratovic等[14]基于Yasui等[6]的直接估计方法,通过附加修正系数来考虑主体结构非线性行为对FRS的影响,并将该方法进一步应用到了多层结构中。Chaudhuri等[15-19]也从不同角度定性或定量地分析了主体结构非线性行为对FRS的影响,总体结论是非线性结构的FRS小于弹性结构的FRS。
尽管楼层反应谱从很早时期就得到了研究,但是其影响因素较多,针对非结构构件的性能评估和设计方法等仍需进一步研究[20-21]。安装软钢阻尼器的减震结构系统在强震下也表现出非线性滞回特征,但与前述弹塑性结构不同的是,该系统中主体结构与屈服耗能阻尼器分离。在减震设计中,有必要考虑主体结构和阻尼器的相互关系,明确阻尼器参数对FRS的影响,从而在多种设计方案中选择最佳的设计参数。因此,本文将针对附加软钢阻尼器的减震结构系统,提出该系统FRS的直接估计方法。基于Yasui等[6]提出的用于弹性结构的FRS估计方法,考虑主体结构和非结构构件周期比以及主体结构阻尼比的影响对该方法进行修正。将减震结构系统等效为黏滞阻尼弹性结构,基于等价弹性结构进行FRS估计计算,并提出主体结构和非结构构件加速度响应降低率性能曲线,分析阻尼器参数对FRS的影响。
1 系统参数设置
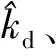
(1)

图1 系统组成及分析模型Fig.1 System Constitution and Analytical Model
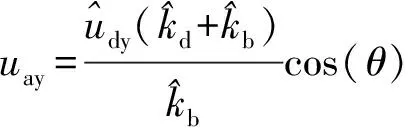
(2)
非结构构件特征参数包括集中质量ms、弹性刚度ks、自振周期Ts、阻尼比ξs和阻尼系数cs。当非结构构件与主体结构的质量比小于0.1%时,两者的耦合作用可以忽略[23]。本文考虑非耦合系统,即该系统中主体结构地震响应不受非结构构件的影响。
2 高阻尼比结构的FRS预测方法
2.1 主体结构周期和阻尼比对FRS的影响
为了分析主体结构周期和阻尼比对FRS的影响,对一组具有不同黏滞阻尼比的弹性结构进行时程分析。设定主体结构自振周期Tf=0.4,1.0,2.0 s,考虑到附加阻尼器后结构的等价阻尼比增加,阻尼比ξf分别取0.05,0.10,0.15,0.20。将《抗震设计规范》[23]的设计反应谱作为目标反应谱,取地表峰值加速度为200 cm·s-2,场地特征周期为0.4 s,通过SeismoArtif软件生成8条持续时间为40 s的人工波,包络曲线采用Saragoni等[24]提出的包络函数。非结构构件周期Ts范围设为0.1~4.0 s,每0.1 s增量定义一个周期,共考虑40种周期,阻尼比ξs=0.03。
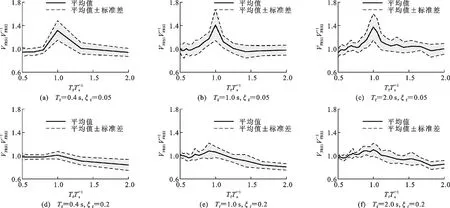
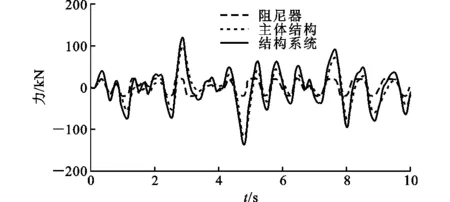
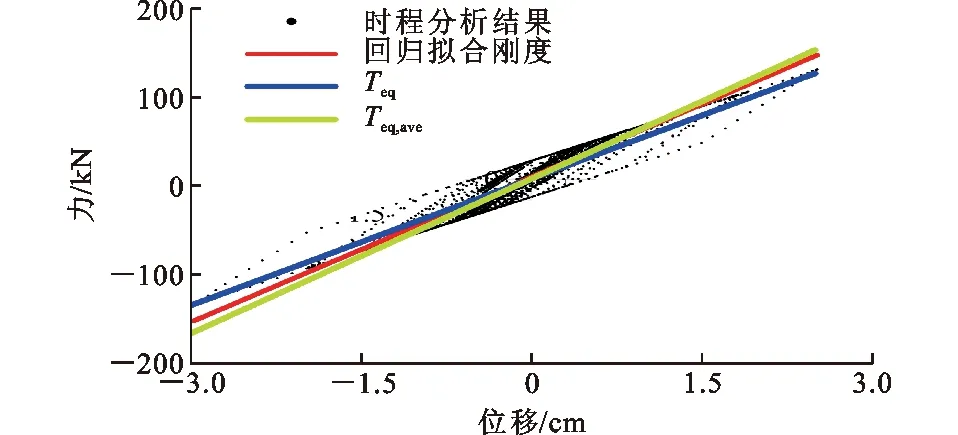
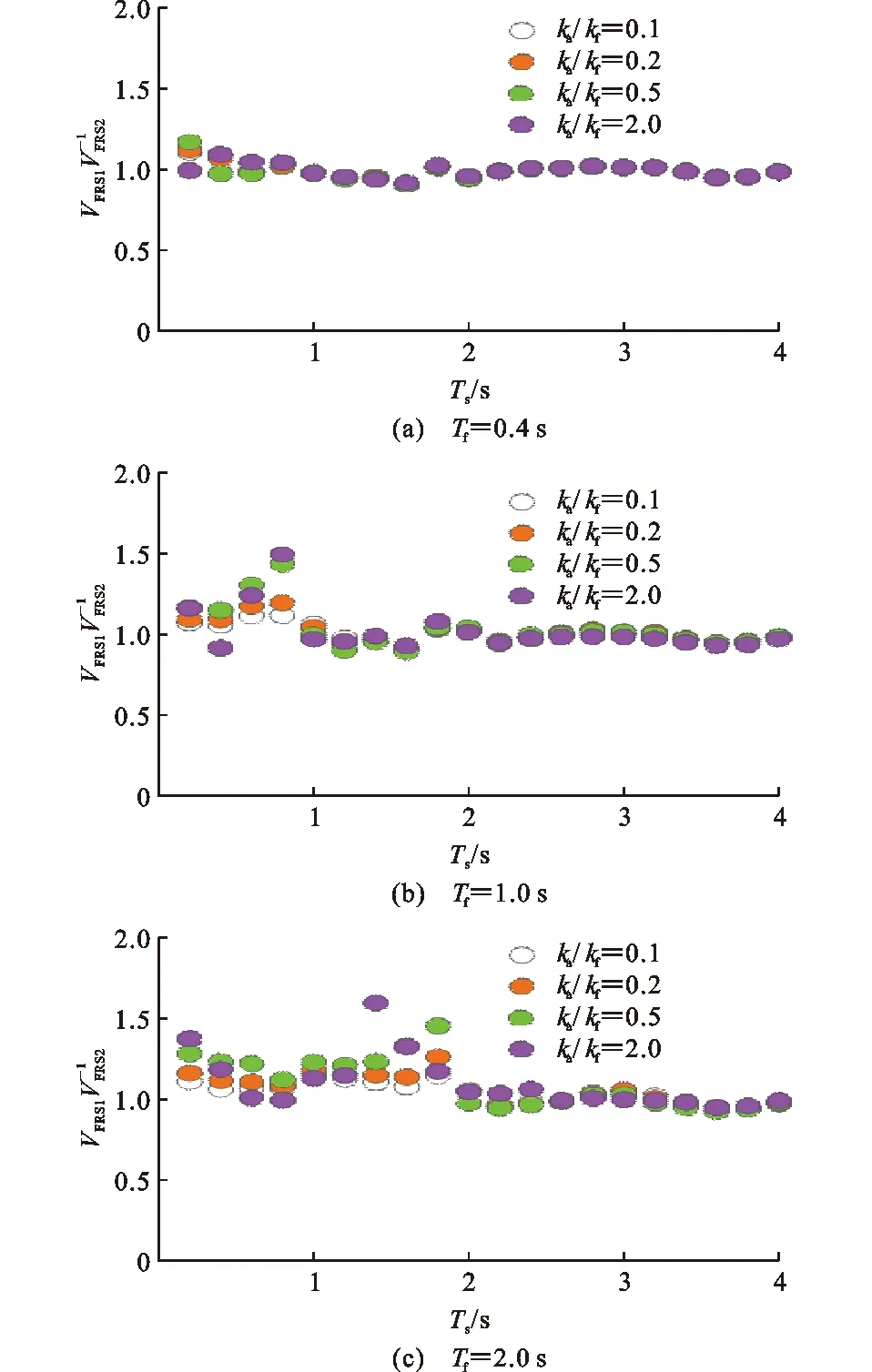
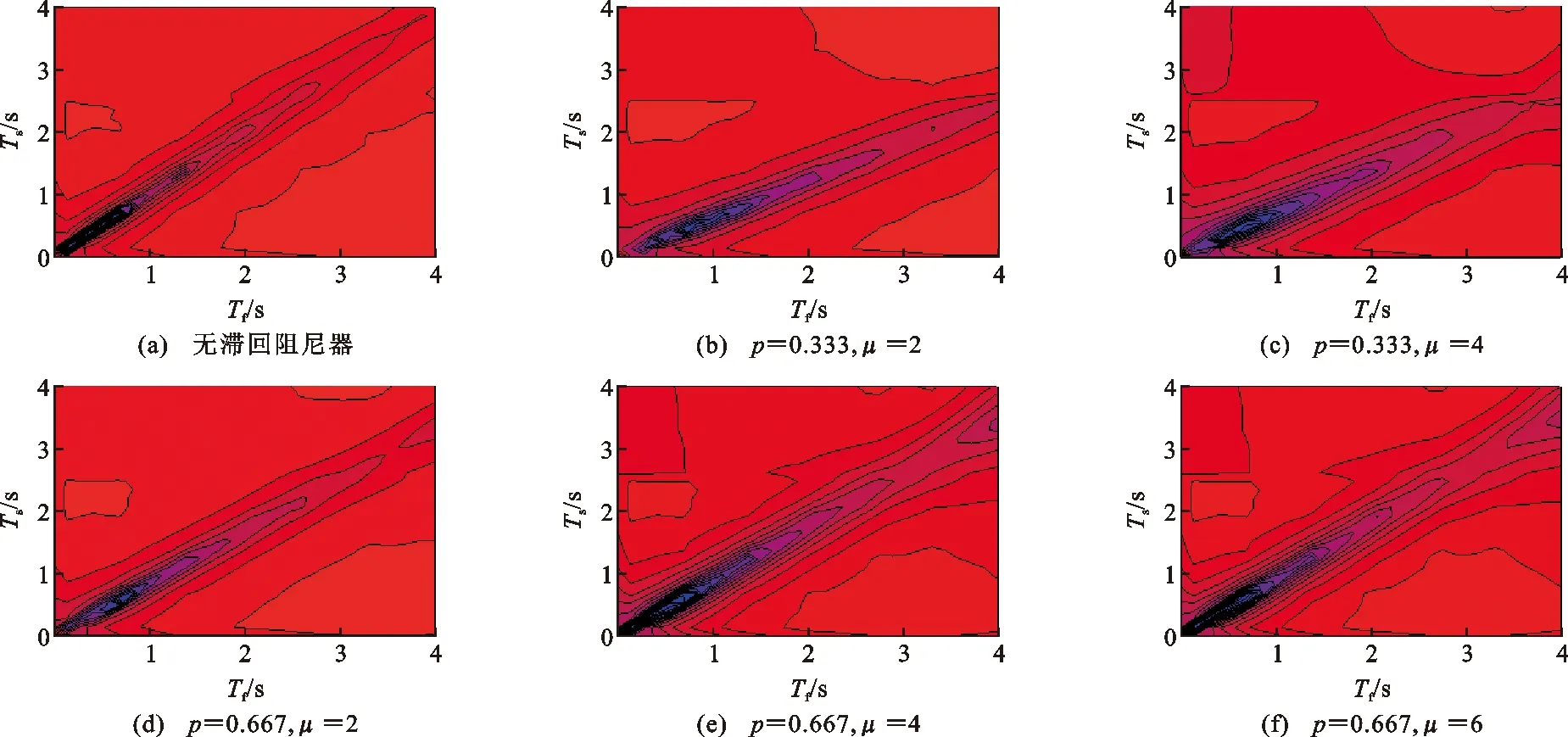
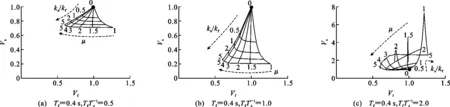
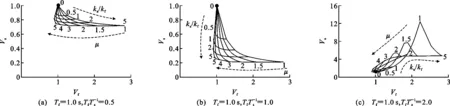
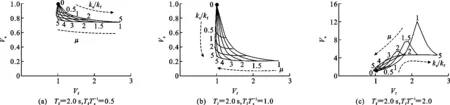
图2为主体结构阻尼比和周期比对FRS的影响。在0.5 图2 主体结构阻尼比和周期比对FRS的影响Fig.2 Influence of Damping Ratio and Period Ratio of Main Structure on FRS (3) 式中:ωf,ωs分别为主体结构和非结构构件的自振角频率;S(·)为地震动反应谱函数。 文献[14],[25]指出式(3)能准确估计非共振范围的FRS,但是过高地估计了共振区的FRS。另外,式(3)仅适用于小阻尼比(0.05)结构的FRS评估,未考虑高阻尼比结构的情况。基于时程分析结果,对式(3)给出的FRS预测结果与时程分析结果进行了比较。图3给出了0.5 图3 FRS预测结果与时程分析结果的比值Fig.3 Ratio of FRS Prediction Results and Time History Analysis Results 下面考虑主体结构阻尼比和周期比Tf/Ts的影响对式(3)进行修正。将FRS预测值与时程分析结果之比表示为周期比Tf/Ts和主体结构阻尼比ξf的函数。采用1stOpt进行非线性回归,得到修正系数的函数关系式。将式(3)除以修正系数就可以得到修正后的FRS预测公式,如式(4)所示,式(4)右边分母部分即为修正系数。图4对比了修正系数的曲线与FRS比值的计算结果。 (4) 图4 修正系数拟合结果Fig.4 Correction Coefficient Fitting Results 主体结构安装软钢阻尼器后,结构系统刚度和耗能能力将发生变化。将该结构系统等效为弹性结构,基于前述FRS方法进行预测。建立等效弹性结构的关键在于确定合理的等价刚度和等价阻尼比计算方法。既有文献多采用系统最大位移对应的割线刚度作为等价刚度[27-29],由此计算相应的等价周期。本文考虑的非线性结构系统,割线刚度对应等价周期Teq,sec如式(5)所示。 (5) 式中:μ为结构的延性系数。 等价阻尼比的计算方法有较多代表性方法[30-33],Kasai等基于平均阻尼比概念[34]推导了双线性滞回系统的平均阻尼比,定义平均阻尼比为振幅从0到最大值所有稳态滞回环的等价黏滞阻尼比的平均值[31]。平均阻尼比是在考虑地震作用下的非稳态响应影响基础上给出的定义。对于双线性滞回系统,平均阻尼比ξeq,ave为 (6) 式(6)的第1项为系统内部黏滞阻尼比,第2项为由阻尼器屈服耗能提供的等价平均黏滞阻尼比。式(5)和式(6)已被证明可以有效地评估双线性滞回系统的峰值位移响应[29-31]。 前述结果已表明,周期比Tf/Ts对共振区FRS的影响非常显著。因此,合理估计非线性减震结构系统的等价周期尤为重要。 图5给出了Tf=1.0 s,Ts=0.8 s,ka/kf=1时系统主体结构和非结构构件的加速度时程曲线。阻尼器延性系数等于5.96。主体结构最大加速度发生在时间t=4.78 s,而非结构构件的最大加速度发生在t=8.97 s。最大位移发生在t=4.8 s,与主体结构最大加速度几乎同一时刻。由图5可知,非结构构件最大加速度出现之前,主体结构有几个振幅相对稳定的往复振动,这种近似的周期性激励将非结构构件的加速度响应激励到峰值。图6为主体结构、阻尼器以及结构系统的力时程曲线。同样可以看到,在非结构构件到达最大加速度位置之前,出现了连续几个振幅相对较高的循环。 图5 主体结构和非结构构件加速度时程曲线Fig.5 Acceleration-time History Curves of Main Structure and Non-structural Component 图6 结构力时程曲线Fig.6 Force-time History Curves of Structure 从图5和图6的时程曲线可以看出,非结构构件的最大加速度并不是由主体结构的最大加速度直接导致,而是由振幅小于最大值的若干个循环的连续激励产生。式(5)中由割线刚度计算得到的等价周期不能很好地代表非线性主体结构对非结构构件的激励周期。因此,本文采用类似式(6)的平均阻尼比概念,将系统等价刚度定义为非线性系统的平均等价刚度,即取振幅从0到最大值所有滞回环割线刚度的平均值。根据该定义,平均等价周期Teq,ave可由式(7)计算。式(8)为非线性结构系统各稳态滞回环的割线刚度对应的等价周期,代入式(7)可求得如式(9)所示平均等价周期的计算公式。图7对比了最大位移时的割线刚度Teq、式(9)得到的平均等价刚度Teq,ave和最小二乘法回归得到的刚度。可以看出,后两者吻合较好,式(9)较好地代表了结构系统在响应过程中的平均刚度。 (7) (8) (9) 图7 力-位移滞回曲线及回归的等价刚度曲线Fig.7 Force-displacement Hysteresis Curves and Regressed Equivalent Stiffness Curves 将式(6)和式(9)代入式(4)得到非线性减震系统的FRS预测公式,如式(10)所示。 (10) 式中:ωeq,ave为Teq,ave对应的平均等价自振角频率。 对附加软钢阻尼器的非线性结构系统进行时程分析,验证式(10)的精度。同样,假定弹性主体结构自振周期Tf= 0.4,1.0,2.0 s,刚度比ka/kf分别设为0.1,0.2,0.5,2.0,附加体系屈服位移uay= 0.5 cm。对以上参数进行组合,得到共计12种结构系统。对各参数组合的结构系统及非结构构件同样考虑0.1~4.0 s范围内的40种周期。 将地震波分别输入各个结构系统中进行时程分析,得到非结构构件加速度响应与对应的结构延性系数μ。将μ代入式(6)和式(9)中计算得到平均等价阻尼比与平均等价周期,最后根据式(10)得到FRS的预测值。图8给出了FRS预测结果与时程分析结果的比值,各点代表所有地震波作用下的平均比值。可以看到,总体上本文提出的平均等价周期和平均等价阻尼比的组合可以较准确地预测FRS,但是在Ts 图8 式(10)FRS预测结果与时程分析结果的比值Fig.8 Ratio of FRS Prediction Results by Eq.(10) and Time History Analysis Results 为了对比结构附加阻尼器后FRS的变化情况,图9给出了附加体系不同刚度比和延性系数组合下FRS随Tf和Ts变化的等值线图,其中虚线代表FRS相对较大的区域,实线代表FRS相对较小的区域。图9(a)为无阻尼器的弹性结构FRS等值线图,在对角线上Tf与Ts相等的共振点,FRS明显大于其他区域,且短周期结构的FRS更大。附加阻尼器后,结构周期减小,FRS较大值会逐渐向水平轴靠近。随着延性系数的增大,等值线分布较为分散,表明FRS随周期的变化趋于平缓。 4.2减震结构的FRS性能曲线 为了定量描述阻尼器参数对FRS的影响,分别定义非结构构件和主体结构的加速度变化率:Vs为附加阻尼器结构系统的FRS相对于无阻尼器弹性结构加速度的比率,如式(11)所示;Vf为主体结构安装阻尼器前后的加速度变化率,如式(12)所示。 (11) (12) 图10~12给出了附加体系的刚度比和延性系数对主体结构和非结构构件加速度响应影响的性能曲线。在绘制性能曲线时,首先给定主体结构和非结构构件的周期,再代入假定的μ和ka/kf,并由式(11)和式(12)分别计算得到加速度变化率。分别代入不同的μ和ka/kf进行重复计算,根据计算结果绘制Vs和Vf的关系曲线,得到性能曲线。图10~12中,主体结构自振周期Tf分别取0.4,1.0,2.0 s,周期比Tf/Ts分别取0.5,1.0,2.0,因此共有9种Tf和Ts的组合。延性系数μ取值范围为1~5,刚度比ka/kf取值范围为0~5。 图10(a)为Tf=0.4 s,Ts=0.8 s时结构的性能曲线。附加阻尼器后主体结构加速度可能减小也可能增大,取决于附加体系延性系数的大小。当μ=1时,结构相当于附加弹性支撑,此时结构的周期减小。如果周期变化后仍处于恒定加速度周期段,主体结构周期的减小将不会改变加速度反应谱值。另一方面,主体结构的阻尼系数不变,随着结构系统刚度的增大,结构系统的阻尼比会降低[式(6)等号右边第2项],因此将导致主体结构加速度响应增大。随着延性系数的增大,等价阻尼比会增大,从而降低主体结构的响应。对非结构构件而言,主体结构附加阻尼器通常会降低非结构构件的加速度响应。因为主体结构附加阻尼器后周期减小,周期比远离共振点,从而导致非结构构件的加速度响应变化。 图9 阻尼器参数对FRS分布的影响Fig.9 Influence of Damper Parameters on FRS Distribution 图10 Tf=0.4 s时结构的性能曲线Fig.10 Performance Curves for Structure with Tf=0.4 s 图11 Tf=1.0 s时结构的性能曲线Fig.11 Performance Curves for Structure with Tf=1.0 s 图12 Tf=2.0 s时结构的性能曲线Fig.12 Performance Curves for Structure with Tf=2.0 s 图11为Tf=1.0时结构的性能曲线。显然,由于安装阻尼器后周期比刚好远离共振点,非结构构件的加速度降低幅度更加显著。周期比的改变是引起加速度变化的主要因素。 图12为Tf=2.0 s时结构的性能曲线。由图12可知,对于特定的延性系数μ,刚度比ka/kf的增大会导致Vs先增大到最大值,然后再逐渐减小。这是因为附加阻尼器后,主体结构系统周期会逐渐接近非结构构件周期,即产生共振。在这种情况下,纵坐标的最大值远大于1,因此减震控制设计中需要特别注意这种情况。随着延性系数的增加,结构的放大效应会逐渐减小。 图11,12的结构性能曲线与图10类似,但各自的Vs和Vf并不相同。由于Tf=1.0 s处于地震动加速度反应谱值随周期变化较为显著的区段,图11(c)中的Vs值大于图10(c)中的值。 通过性能曲线可以发现,评估减震结构FRS需综合考虑附加体系刚度比、延性系数以及主体结构周期的影响。通过绘制性能曲线,可以全面了解阻尼器参数对FRS的影响,并能为阻尼器参数优化设计提供有益参考。 由于采用了等价线性化方法,非线性结构系统与等价线性系统的FRS之间仍不可避免地存在若干误差。式(4)的修正系数基于黏滞阻尼结构得到,由于最大力与最大位移之间相位差的不同,将基于黏滞阻尼系统得到的公式应用于滞回系统会产生一定的误差。在计算高阻尼比的反应谱时,采用了规范设计反应谱的计算公式,规范反应谱中的阻尼调整系数一般会低估阻尼比增加对反应谱的降低效果[27]。另外,式(4)中的修正系数是统计回归得到,将其应用于特定地震动作用下的结构系统时也会产生一定的误差。 (1)Yasui等针对弹性结构提出的FRS直接估计方法在0.5 (2)在原方法的基础上提出了修正的FRS计算方法,修正公式可用于周期比为0.5 (3)将等价线性化方法应用于附加软钢阻尼器的减震结构能较好地进行非线性系统的FRS估计。 (4)提出了FRS性能曲线的绘制方法,将阻尼器参数对FRS的影响可视化,可以帮助设计人员全面理解附加阻尼器后结构系统的FRS变化。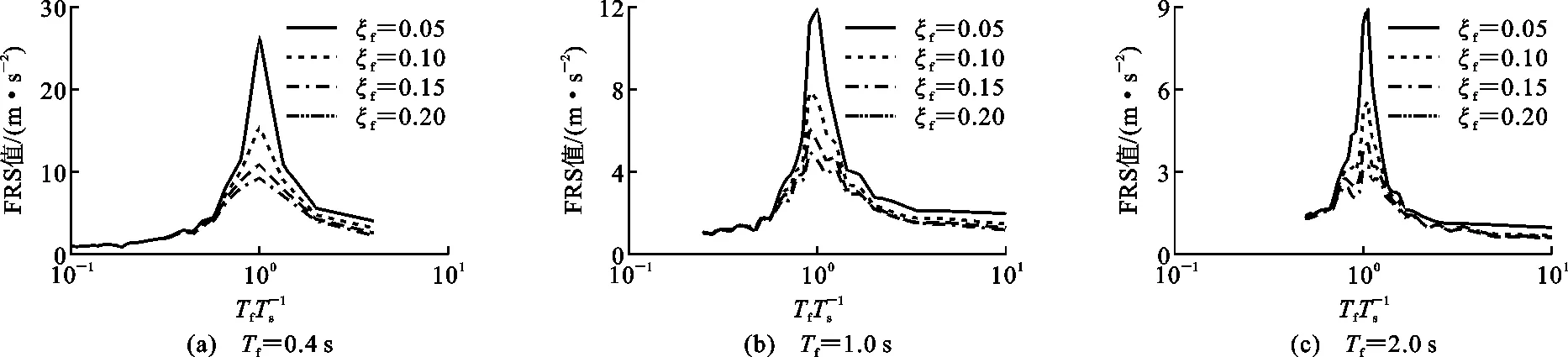
2.2 考虑主体结构阻尼比影响的FRS评估
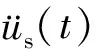

3 减震结构系统的FRS预测方法
3.1 结构系统的等价周期

3.2 减震结构的FRS预测
4 阻尼器参数对FRS的影响
4.1 阻尼器对FRS分布特征的影响
4.3 评估方法的误差
5 结语
