基于多性能指标的轻木-混凝土混合结构层间隔震

王雪亮，王秀鑫，魏凯睿，徐乾罡

(1. 武汉理工大学道路桥梁与结构工程湖北省重点实验室，湖北武汉 430070；2. 武汉理工大学土木工程与建筑学院，湖北武汉 430070)

0 引 言

轻型木结构由于轻质高强、施工简便、抗震性能好、绿色环保等优点而越来越受到人们的青睐。轻木结构主要应用于3层及3层以下的住宅建筑，在推广中受到很大限制，因此出现了与其他材料结构组合而成的木混合结构。将轻型木结构“上嫁”于低层混凝土结构的木-混凝土混合结构为主要结构形式之一，已经在国内外开始应用，如伦敦的Stadthaus公寓为底部一层钢筋混凝土结构、上部8层正交胶合木(CLT)结构的混合结构；墨尔本的Forte建筑为首层商用混凝土结构、上部9层轻木结构住宅[1]；成都青白江小学为底部1层混凝土、上部2层木结构的教学楼。这种结构形式兼具2种结构的优点，既可提供底部混凝土框架大空间，又能达到绿色环保的目的，具有较大的工程应用空间。

由于木材与钢筋混凝土刚度悬殊，其上部木结构的地震反应相比纯木结构有明显的放大。日本的Isoda等[2]研究了底层混凝土、上部不同层数轻木结构的抗震性能，发现上部结构的刚度和质量对地震力有明显影响。熊海贝等[3-6]对该混合结构进行了系统的理论分析、有限元模拟及地震模拟振动台试验研究，结果表明：上下刚度比对结构反应有非常明显的影响，上部木结构的位移响应远大于下部混凝土结构，其顶层加速度放大系数最大可达6，而且破坏主要发生在轻木结构的首层，明显大于同等条件下的纯木结构。

针对这一问题，何敏娟等[7]基于传统抗震设计理论，建立了轻木-混凝土上下混合结构的抗震设计方法。在强震区，采用这种传统抗震方法仍然无法避免上部结构的损坏，且不太经济。据此谭柱[8]借鉴斗拱的构造及耗能机理，设计了一种新型木制隔震装置。本文基于该装置的试验研究结果，将其应用于上木下混结构形成层间隔震体系，并对其进行了层间隔震效果分析。为获得最优隔震效果，采用层间隔震体系的三质点动力模型对其进行了多性能指标的参数优化设计，确定木制隔震层的最优参数区间。

1 木制隔震装置耗能机理

新型木制隔震装置是一种多级复合隔震装置，采用原木或工程木制作，无需金属连接件，由栌斗、泥道拱、华拱、散斗等多层短木部件交错叠置，层层锁扣，利用木材接触面的摩擦滑移、木材剪切、弯曲及挤压等非线性变形耗散能量，达到层间隔震的目的。该装置传承古建筑斗拱的构造特点，如图1所示，置于建筑的中间楼层，上部承接轻木结构的地梁板，底部与混凝土结构的顶部相连接，既能美观建筑立面，又能起到明显的层间隔震作用，具有较强的工程应用价值。

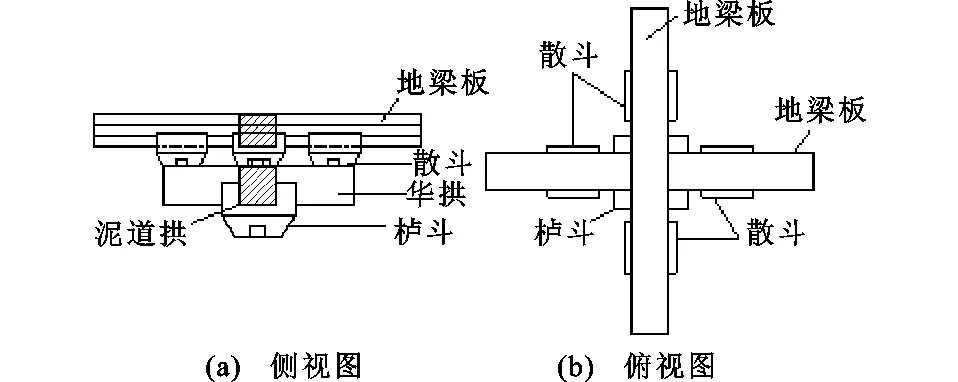
图1 木制隔震装置构造Fig.1 Structure of Wooden Isolation Device

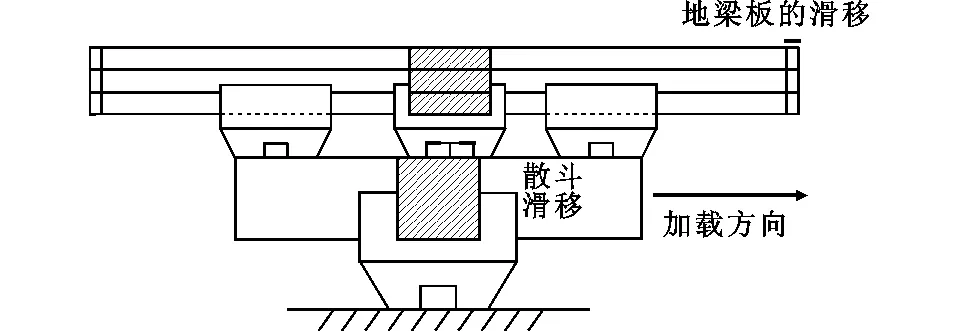
图2 隔震装置滑移Fig.2 Sliding of Isolation Device

新型木制隔震装置的滑移主要发生在地梁板及散斗、散斗与拱之间，其耗能机理不同于传统斗拱[9]。传统斗拱榫卯之间联系紧密，在底部馒头榫相对普拍枋发生滑移前，主要依靠斗拱的摇摆回转变形耗散能量[10]。新型木制隔震装置具有多级耗能特征：上部轻木结构的地梁板置于散斗顶部U形槽，在侧向力作用下发生滑动；同时，在散斗底部的卯口为条形槽，泥道拱及华拱的榫头在克服摩擦力后可以沿条形槽左右滑动，主要通过摩擦滑移耗散地震能量，当滑移至条形槽端部后，还可以利用木材的非线性特性进一步耗散地震能量。

为了研究该装置的承载能力和耗能性能，对木制隔震装置进行了水平及竖向静载和低周反复荷载试验。结果表明：该隔震装置在竖向静荷载作用下最终栌斗劈裂破坏，承载力可达到80 kN。水平静力加载力-位移曲线如图3(a)所示，隔震装置在水平向克服静摩擦力后，具有较好的滑移及变形能力，最大水平侧移可达116 mm，由于材料的非线性变形耗能，承载力大于滑动摩擦力。当侧向位移幅值达36 mm时，在华拱和泥道拱2个侧移方向的滞回曲线如图3(b)，(c)所示。当华拱侧向位移幅值达60 mm时，滞回曲线如图3(d)所示。由图3(d)可知，2个方向的滞回曲线都比较饱满，具有良好的耗能能力。木制隔震装置从开始受力就具有耗能能力，滞回环为梭形；当达到最大静摩擦力后，榫头开始在散斗的凹槽内滑动，水平力为滑动摩擦力；当达到滑移限值后，隔震装置利用材料的非线性变形仍然可以产生更大侧移，侧向力有所增大。

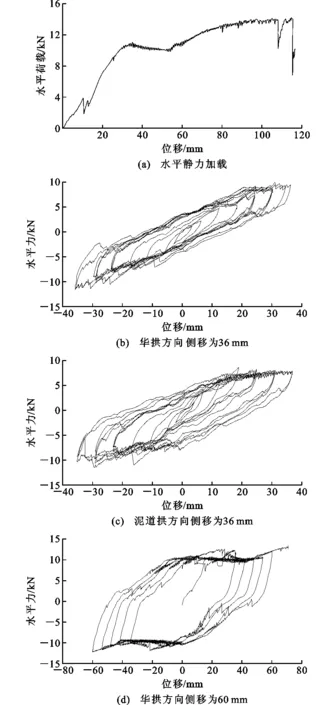
图3 荷载-变形曲线Fig.3 Load-deformation Curves

2 多质点模型地震响应分析

以5层轻木-混凝土结构为工程背景，在2种结构的连接层设置木制隔震装置，并利用Bouc-Wen恢复力模型[11-12]来模拟木制隔震装置，建立该层间隔震结构的多质点模型，并进行地震响应分析。

2.1 轻木-混凝土结构方案

以某小学3层轻木结构校舍[13]为原型在底部添加2层混凝土结构形成5层木-混凝土混合结构，每层层高为3.6 m，长为26.4 m，宽为15.8 m，上部木结构平面布置如图4(a)所示，下部混凝土采用C30，结构布置如图4(b)所示，框架柱尺寸为400 mm×400 mm。设防烈度为8度，Ⅱ类场地，地面加速度为0.2g(g为重力加速度)，特征周期为0.45 s。

图4 轻木-混凝土混合结构平面图(单位：mm)Fig.4 Plan of Light Wood-concrete Hybrid Structure (Unit:mm)

2.2 隔震层的布置

在上下部结构连接处布置隔震层，由于隔震层承受上部木结构质量，根据试验测得的木制隔震装置竖向承载力及水平刚度进行了隔震层初步设计，共设置104个木制隔震装置，华拱与横轴一致，如图5所示。

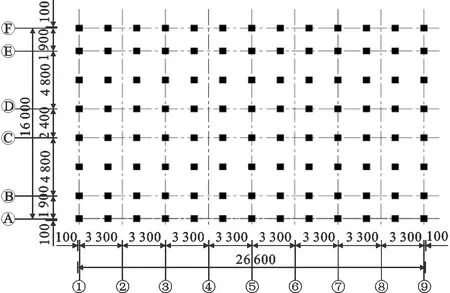
图5 隔震装置布置平面图(单位：mm)Fig.5 Layout Plan of Isolation Dampers (Unit:mm)

2.3 层间隔振结构的多质点模型

由于结构具有对称性，不考虑结构扭转效应，根据木-混凝土层间隔震结构的振型及静力作用下的变形特点，将隔震结构简化为多质点剪切模型，如图6所示，其中各层质量mi按各楼层的重力荷载代表值方法计算,kb为隔震层的刚度，隔震层质量mb为隔震层楼板质量与相邻楼层半高度质量的和。

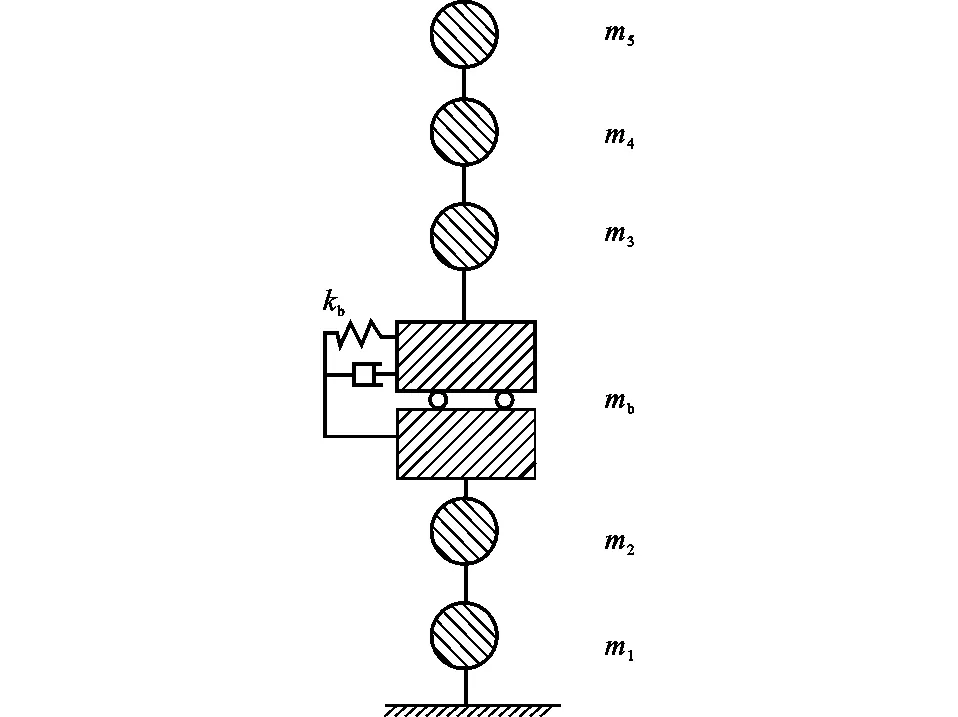
图6 层间隔震结构的多质点动力模型Fig.6 Multi-lumped Mass Dynamic Model of Inter-story Isolation Structure

多质点模型混凝土结构的刚度根据D值法计算，轻木结构的各层刚度为各木剪力墙的刚度之和。各质点等效质量与侧向刚度如表1所示，动力平衡方程为

(1)

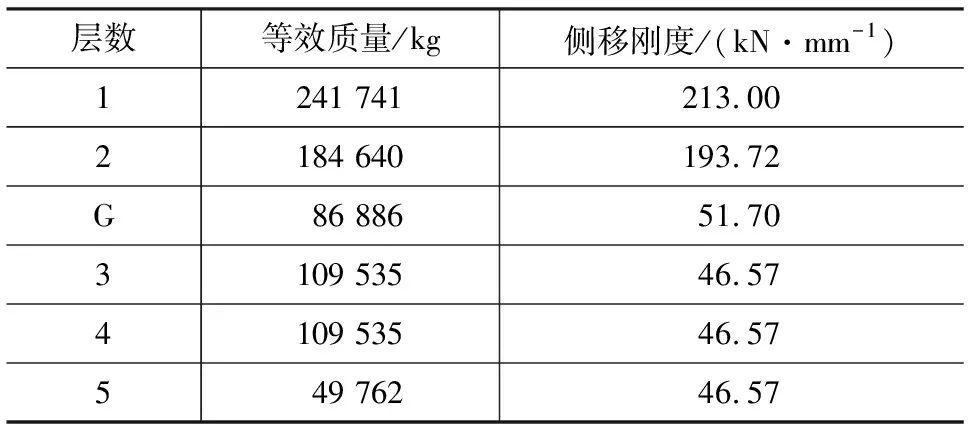
表1 结构的等效质量与华拱向侧移刚度Tab.1 Equivalent Mass of Structure and Lateral Stiffness in Huagong Direction

注：G表示隔震层。

由于隔震层的阻尼与原结构相差很大，层间隔震结构为典型的非经典阻尼结构，故采用上下子结构法确定整体结构的阻尼系数矩阵，即将原结构在隔震层分为上下2个子结构，分别对子结构进行模态分析，计算各自的瑞雷阻尼矩阵Ct与Cb，而隔震层的耗能特性采用隔震支座的试验结果，即拟合Bouc-Wen恢复力模型模拟，从而确定层间隔震结构的多质点动力模型。

2.4 地震波的选取

参照《建筑抗震设计规范》(GB 50011—2010)[14]，根据此建筑的II类场地条件选取El Centro波与唐山波2条强震观测波作为地震输入。分别将其加速度幅值调整至多遇、罕遇地震下对应的幅值，即0.7，4 m·s-2，地震波双向输入；2条地震波幅值为0.7 m·s-2时的加速度时程曲线如图7所示。

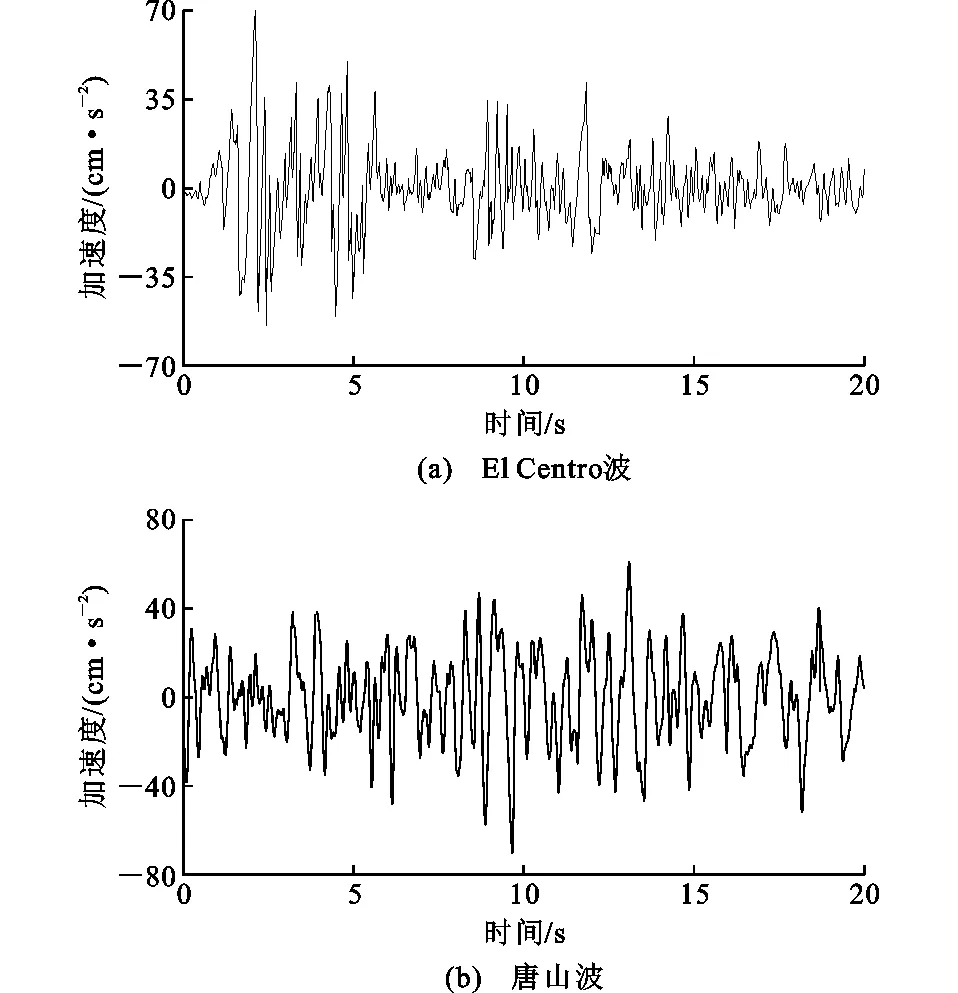
图7 地震波加速度时程曲线Fig.7 Acceleration Time-history Curves of Seismic Wave

2.5 多遇及罕遇地震作用下多质点模型地震响应

采用自适应步长的4阶龙格库塔法[15]求解多质点模型的运动方程，并编制MATLAB程序计算在多遇与罕遇地震作用下的结构反应。

多遇地震作用下，El Centro波、唐山波作用下隔震层的滞回曲线分别如图8(a),(b)所示。在多遇地震作用下，此隔震装置能起到一定的减震效果，但由于地震力过小，无法使隔震支座产生充分的滑移，故减震效果并不理想。罕遇地震作用下，El Centro波、唐山波作用下隔震层的滞回曲线分别如图9(a),(b)所示。

图8 多遇地震下隔震装置的滞回曲线Fig.8 Hysteretic Curves of Isolation Device Under Frequent Earthquakes

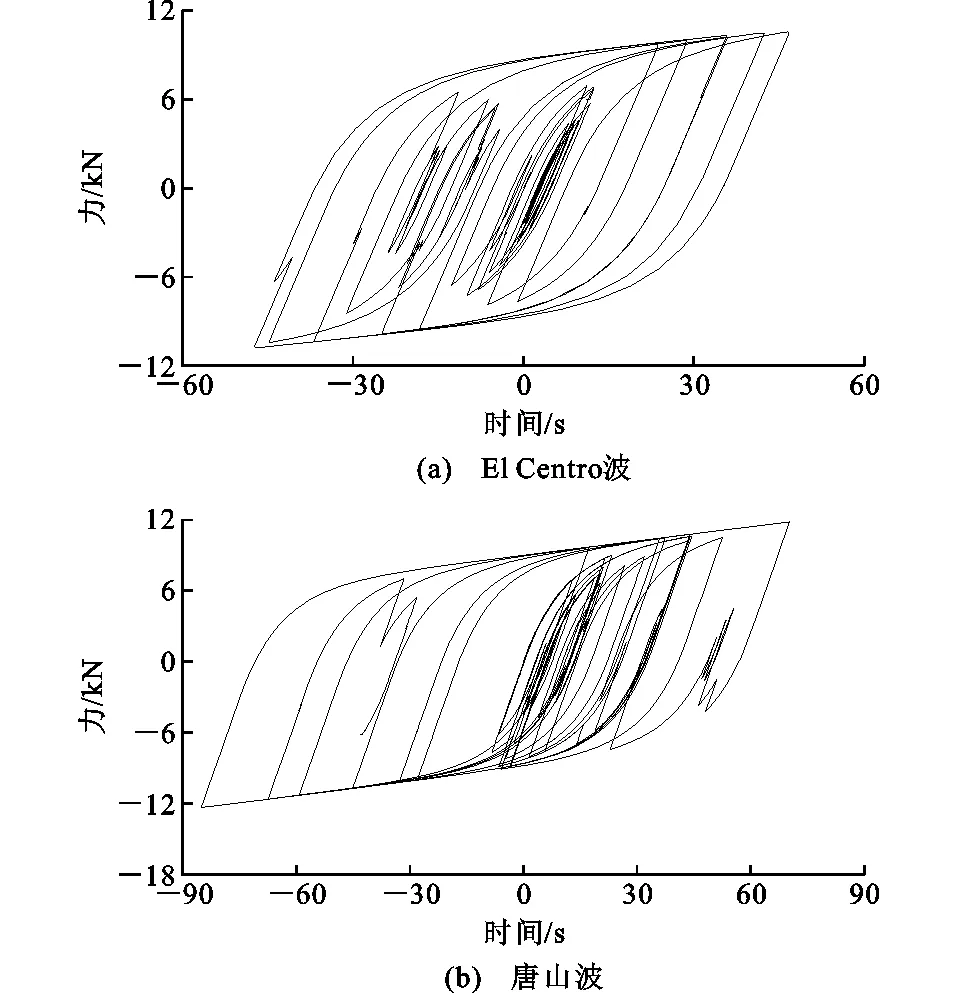
图9 罕遇地震下隔震装置的滞回曲线Fig.9 Hysteretic Curves of Isolation Device Under Rare Earthquake

由图9可知，在罕遇地震作用下，隔震层的滞回曲线非常饱满，表明隔震装置已经进入塑性变形的强化阶段，充分发挥了滑动与塑性二次变形的耗能能力，对上部木结构产生明显的隔震作用。在El Centro波作用下，层间隔震结构与非隔震结构的顶点位移时程曲线比较如图10所示。各层最大层间侧移及最大加速度如表2，3所示。

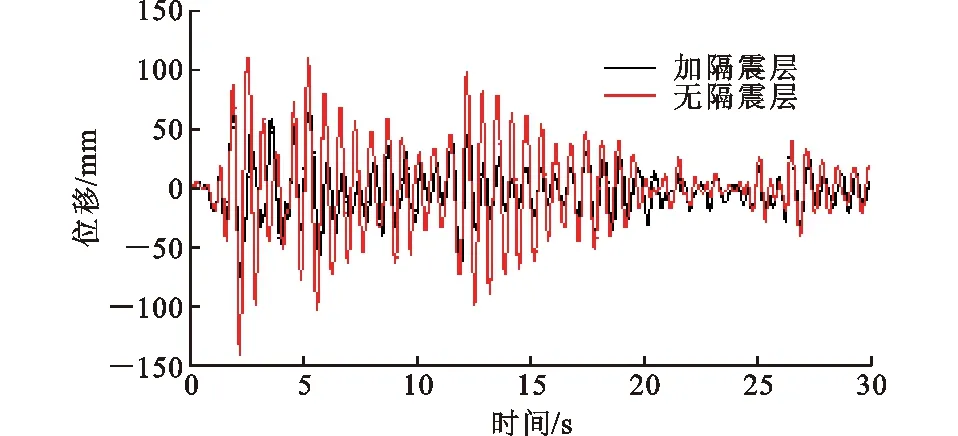
图10 结构顶点处位移时程曲线Fig.10 Time-history Curves of Top Displacement

由图10可知：原结构在地震作用下产生了剧烈的“鞭梢效应”，相比于低层混凝土结构，轻木结构的层间侧移及加速度都被明显放大；设置此隔震装置后，减震效果明显。隔震结构的顶点位移比原结构减小了47.2%，除隔震层外，其他各层的层间侧移都有明显减小，尤其是首层轻木结构的层间侧移仅为原结构的44.35%；上部木结构的加速度也明显减小，首层木结构加速度值不及原结构的50%，但混凝土结构的加速度减小非常有限，甚至在唐山波作用下略有放大。

表2 华拱向最大层间位移Tab.2 Maximum Inter-story Drift in Huagong Direction

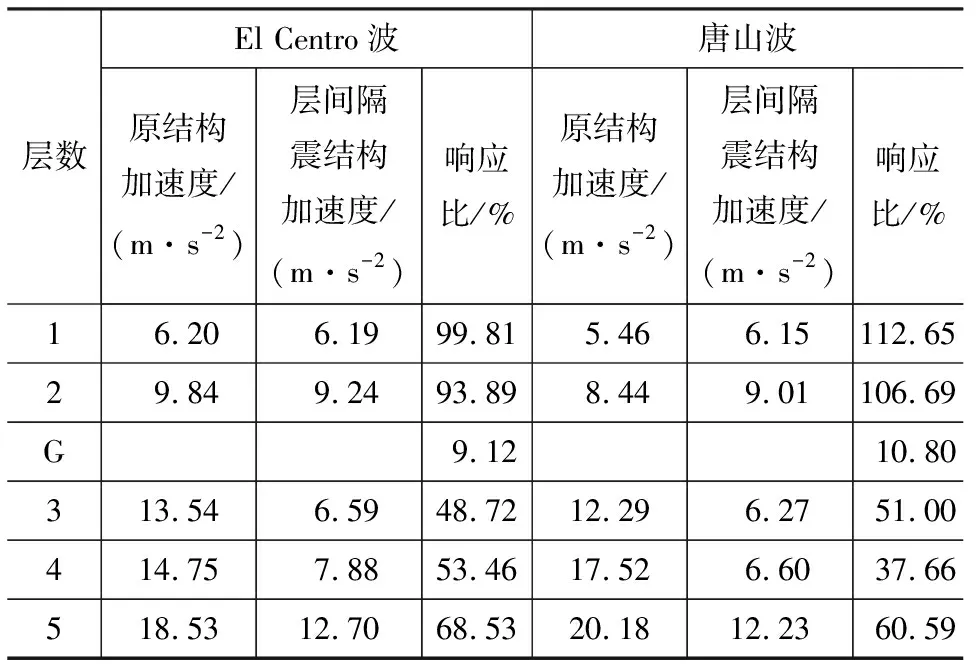
表3 华拱向最大绝对加速度Tab.3 Maximum Absolute Acceleration in Huagong Direction

3 基于三质点模型的参数优化分析

虽然设置木制隔震装置的轻木-混凝土混合结构已经具有明显的减震效果，但是上部轻木结构较柔，明显存在一定的振动响应，而且下部混凝土结构有加速度放大的现象，因此有必要进行参数优化，选取合适的隔震层刚度与阻尼以提高隔震效果。层间隔震结构的参数优化常采用两质点[16]或多质点等效模型，由于上部结构较柔，不能将其视为刚体移动，故采用三质点模型以考虑上部结构的振动响应。

3.1 层间隔震结构的等效三质点模型

将上部结构、隔震层及下部结构分别等效为1个质点，形成三质点动力模型，如图11所示。隔震层与隔震层以上结构质点的相对位移便可反映上部木结构的地震响应。

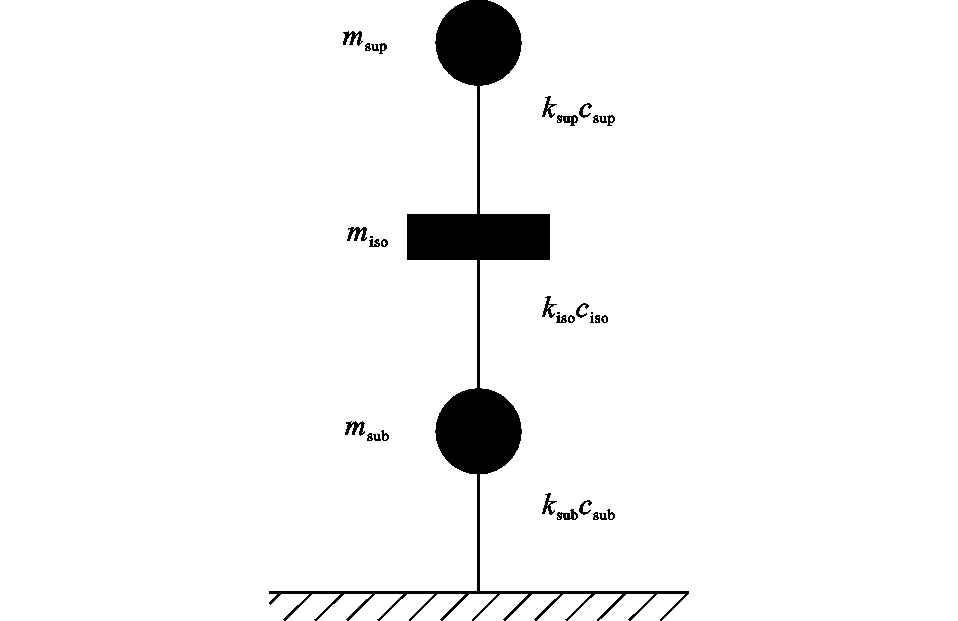
图11 三质点模型Fig.11 Three-lumped Mass Model

上下部子结构的等效质量msup，msub及等效刚度ksup，ksub的等效简化采用以下方法[17]：首先求解上下部子结构的各阶频率ωi(i=1,2,…,n)与对应的各阶振型φi(i=1,2,…,n)，计算等效质量meq与等效刚度keq为

(2)

(3)

式中：r为将地面位移与模型自由度耦合的影响向量；φ1为第1阶振型。

由此分别得到上、下部子结构的等效质量msup，msub与等效刚度ksup，ksub。

上、下部子结构的阻尼系数c为

c=2meqω1ξ

(4)

式中：ξ为子结构的阻尼比，文中均取0.05。

隔震层的质量miso与等效刚度kiso通过试验确定。隔震层阻尼系数ciso为

ciso=2(miso+msup)ωisoξiso

(5)

(6)

式中：ξiso为隔震层等效黏滞阻尼比，通过试验确定。

模型等效后，三质点模型与多质点模型周期对比如表4所示。

表4 三质点模型与多质点模型周期对比Tab.4 Comparison of Periods Between Three-lumped Mass Model and Multi-lumped Mass Model

由表4可知，三质点模型与多质点模型的前3阶周期十分接近，相对误差皆在6%以内，表明此简化模型可以准确反映结构的前3阶模态。

3.2 层间隔震的参数优化分析

隔震层的参数优化设计采用频域分析法[18-20]。对于层间隔震结构通常选取基底剪力为最优控制目标[21]。假设输入的地震波是均值为0的平稳随机过程，则系统的响应也是均值为0的平稳随机过程。分别以基底剪力F、上部结构层间侧移及下部结构加速度为最优控制目标，经过傅里叶变换，并取隔震层质量为单位1，计算可得剪重比的均方差为

μsubRe(Ha1(iω)Ha2(iω))+

2μsupRe(Ha2(iω)Ha3(iω))+

μsupμsubRe(Ha2(iω)Ha3(iω))]dω}/g

(7)

下部结构绝对加速度均方差为

(8)

上部结构层间侧移的均方差为

|H3(iω)|2+2Re(H2(iω)H3(iω))]dω}

(9)

式中：比例参数μsup，μsub分别为上、下部结构与隔震层质量比；Ha1，Ha2，Ha3分别为质点msub，miso，msup的绝对加速度传递函数；H2，H3分别为miso，msup的位移传递函数；ω为频率；σ(·)为均方差。

对于既定结构，μsub，μsup，ωsub，fsup4个参数为恒定值，隔震层参数ξiso，fiso为待定控制参数。

对于本文的木混结构，根据上下部的结构质量及刚度，可计算既定参数(表5)。

表5 三质点简化模型参数Tab.5 Parameters of Three-lumped Mass Simplified Model

注：ωsub为下部结构频率；fsup为上部结构与下部结构的频率比。

在给定结构参数的情况下，可以绘制剪重比、下部结构绝对加速度(上部结构层间位移)与隔震层阻尼比ξiso及频率比fiso关系的三维图像，见图12。

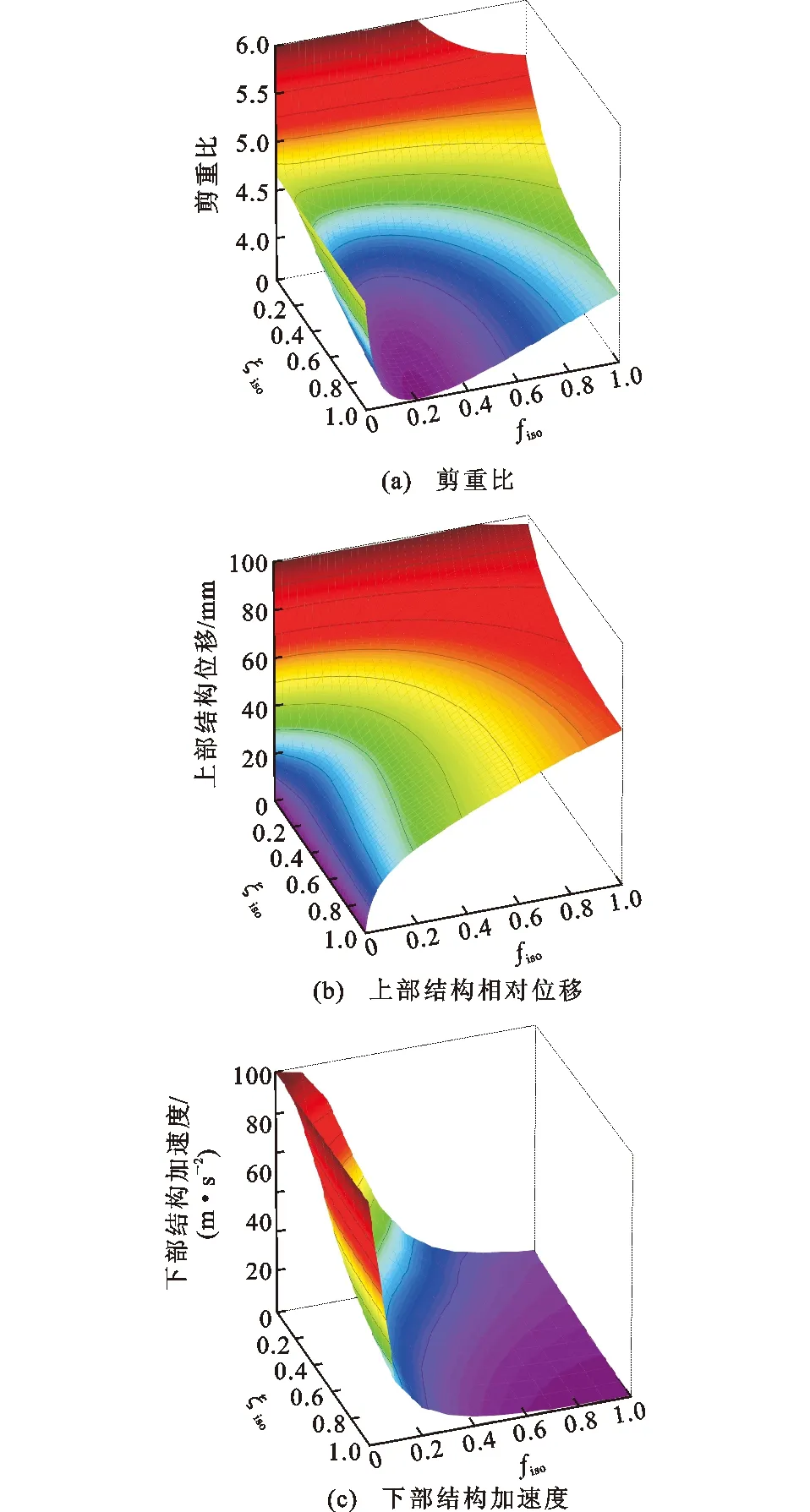
图12 三性能指标-频率比-阻尼比关系Fig.12 Relationship of Three Performance Indicators, Frequency Ratio and Damping Ratio

由图12(a)可知:当隔震层阻尼比为0时，基底剪力随着频率比的增大呈下降的趋势；在非0情况下，随着阻尼比的增大，基底剪力不断减小，但减小速度不断放缓；当阻尼比大于0.2后，增大阻尼比对基底剪力的影响有限。当频率比为0时，基底剪力为固定值，改变阻尼比对基底剪力没有影响；随着频率比的增大，基底剪力迅速减小；当隔震层频率比位于0.2附近时，基底剪力达到最小，当频率比大于0.2后，又开始逐渐增大，频率比处于0.2～0.4区间；阻尼比大于0.1时，基底剪重比均控制在4.0以下。由图12(b)可知，当频率比与阻尼比均为非0时，上部结构的层间位移随着频率比的增大而增大，隔震层刚度越小，上部结构的位移越能得到有效抑制。当频率比小于0.7时，相对位移首先随着阻尼比的增大而减小至最小值，然后随着阻尼比的增大而有轻微增大。因此对于不同的频率比存在不同的最优阻尼比，如隔震频率比为0.3时，隔震层最优阻尼比约为0.42；频率比为0.2时，最优阻尼比为0.31，最优阻尼比在一定范围内时，相对位移都可得到有效控制。更为关键的是频率比的控制，当频率比小于0.4、阻尼比大于0.15时，结构的相对位移均可控制在原结构的50%以下；当频率比小于0.3、阻尼比大于0.2时，仅为原结构的1/3。

由图12(c)可知，下部结构的加速度响应随着隔震层阻尼比、频率比的增大而减小。当隔震频率越小、隔震层越柔，下部结构的加速度越可能出现增大。在进行隔震设计时，应控制隔震层的刚度不宜过柔，适当增大阻尼比以减小下部结构的加速度。数据分析表明：当频率比大于0.2、阻尼比大于0.1时，下部结构的加速度均小于原结构。

综上所述，依据剪重比、上部结构相对侧移及下部结构加速度，可以取隔震层最优频率比在0.2～0.4区间，最优阻尼比根据频率比的不同在0.15～0.4区间确定。

4 结语

(1)新型木制隔震装置既传承古建筑斗拱的构造特点，又适用于现代木结构，具有潜在的工程应用价值。试验结果表明：木制隔震装置具有足够的水平竖向承载力及良好的耗能能力。

(2)采用木制隔震装置对上木下混混合结构进行层间隔震，并采用多质点动力模型进行地震响应分析，结果表明：在多遇地震作用下，结构几乎处于弹性阶段，隔震装置未发生滑移，减震效果不明显；在罕遇地震作用下，隔震支座产生了充分的滑移，并进入二次变形阶段，滞回曲线饱满，耗能充分，但下部结构存在加速度放大现象。

(3)分析隔震层参数对上木下混隔震体系隔震效果的影响，以上层结构层间位移、下部结构加速度及底部剪力为最优控制目标，进行参数优化分析，结果表明：隔震层最优频率比在0.2～0.4区间，最优阻尼比根据频率比的不同在0.15～0.4之间确定，结构的减震效果可以达到最优。