济南轨道交通S1线坐标系统建立的实践与研究
2020-01-14朱君张强
朱君,张强
(1.济南市勘察测绘研究院,山东 济南 250101; 2.山东省城市空间信息工程技术研究中心,山东 济南 250101)
1 引 言
根据《城市轨道交通工程测量规范》的要求,城市轨道交通工程测量应采用所在城市的平面坐标和高程基准。城市间的轨道交通工程以及与城市轨道交通工程结构、线路衔接或联系的其他工程应采用统一的平面坐标和高程系统,平面坐标和高程系统不一致时应建立转换关系。
同时,当不考虑高程投影时,若使高斯正投影变形值不大于1/40000,将投影带边缘至中央子午线的距离控制在 45 km以内[1];当线路轨道面平均高程的边长高程投影长度变形和高斯投影长度变形的综合变形值大于 15 mm/km时,线路控制网和线路加密控制网应采用抵偿高程面作为投影面的城市平面坐标系统,或者高程投影面不变,采用高斯-克吕格任意带平面直角坐标系统[2]。
济南市目前已建立了轨道交通R1、R2、R3线三条线路的控制网,平面坐标和高程系统均采用与济南市城市平面坐标和高程系统一致的1993年济南市独立坐标系(以下简称“93坐标系”)、1985国家高程基准。轨道交通S1线是即将开展的一条新线路,线路最东端距离当前93坐标系的中央子午线约 51 km,大于理论分析值,93坐标系在章丘区区域的使用已经不满足相关规范的技术规定,需要建立新的坐标系统和转换关系。
2 项目现状情况分析
2.1 轨道交通S1线的线位情况
轨道交通S1线西自济南市工业南路,沿世纪大道东行至章丘区三涧大道,全长约 40 km,最西端距离中央子午线约 11 km,最东端距离中央子午线约 51 km,高程自 51 m~126 m,具体的高程起伏见轨道交通S1线纵断面图(截取),如图1所示。按照目前的93坐标系参数,根据轨道交通S1线实际线位及周边高程情况,分析轨道交通S1线的实际变形。

图1 S1线纵断面示意图
2.2 长度综合变形的因素
引起长度变形主要因素:
(1)量测边长归算到椭球面上,长度缩短,其变形影响为△S1;
其中,Hm为归算边高出椭球面的平均高程,S为归算边的长度,R为归算边方向椭球法截弧的曲率半径(一般取值为 6 371 km)[3]。
(2)将椭球面上边长归算到高斯投影面上,长度增加,其变形影响为△S2。
其中,S1为投影归算后的边长,ym为归算边两端点横坐标平均值,Rm为椭球面平均曲率半径(一般取值为 6 371 km)。
(3)长度综合变形公式
由以上两种因素造成的长度综合变形公式,即为:
△S=△S1+△S2
2.3 项目实际变形计算
根据轨道交通S1线纵断面的起伏,进行采样计算。计算数据如表1所示。
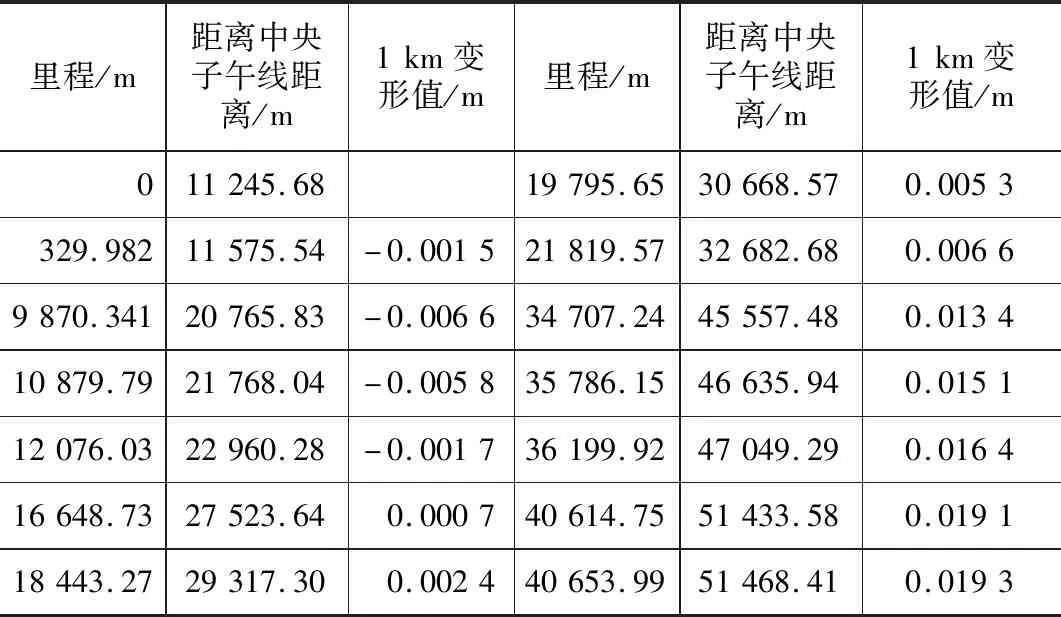
S1线投影变形采样点数据计算表 表1
通过以上的计算,超限的区域基本在距离中央子午线 46.6 km以东区域。
3 坐标系的建立方法选择与分析
3.1 长度综合变形超限的处理方法
(1)高斯投影于参考椭球面上任意带平面直角坐标系。
以城市区域中心地理位置设定独立坐标系的高斯投影中央子午线,投影面在椭球面上,通常采用高斯投影计算方法实现[4]。
(2)高斯投影于高程抵偿面的任意带平面直角坐标系。
3.2 确定坐标系的建立方法
(1)建立新坐标系,需要选择数学模型,主要从以下两个方面考虑:
①考虑原城市独立坐标系的设置,目前市区内的轨道交通线路采用的坐标系为93坐标系,在章丘区如果采用椭球变换产生新的坐标系,将对两套坐标系衔接及实际应用都带来很多问题,所以本次拟采用原椭球参数来建立,经资料收集和推算,原椭球采用椭球膨胀法建立[5],建立方法如下:
以独立坐标投影面的大地高作为椭球平均曲率半径的变动量,反求椭球长半径的变动量[8]。则新椭球平均曲率半径及长半轴如下:
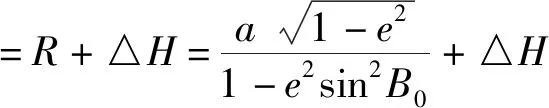
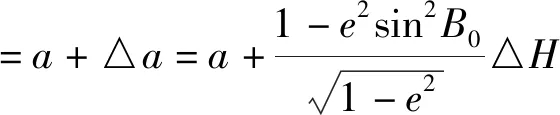
②以最大可能地减少转换数据量和数据转换难度。
(2)如果考虑在保障椭球参数不变的情况下进行设计,则可以采用以下两种方法:
①采用抬高投影面的方法,抬高投影面法通过将济南市原市区与章丘区采用不同的高程投影面,使长度的综合变形达到规范要求,这种方法的优点是可以保证济南市区与章丘区的紧密衔接,只是在变形比例上存在不一致,但仍能满足规范要求,缺点是控制范围有限,一旦离开了当前测算的有效区域,变形将呈几何级增长[6]。
②采用任意带中央子午线法,采用高斯投影任意带中央子午线法可以在最大限度不改变椭球参数及投影面的情况下,通过坐标换带即可完成[7]。优点是控制范围大,对于章丘区以后的轨道交通线路如果超出了目前的控制范围也适用,缺点是在公共分带区域的衔接上,需处理好地形图接边,公共施工控制点的衔接等问题。
经过讨论及研究相关类似线性工程的做法,决定采用第二种方法进行坐标系的设计。
4 关键技术路线及实现方法
4.1 主要内容
(1)通过计算长度综合变形,确定任意带中央子午线、投影面高度;
(2)确定原点位置及坐标加长数;
(3)通过重叠带变形差,确定重叠带宽度;
(4)求解新中央子午线下的控制点坐标;
(5)求解新中央子午线下的坐标转换七参数;
(6)验证坐标转换的正确性。
4.2 确定任意带中央子午线
通过计算,针对轨道交通S1线的线位及周边高程情况,选择采用一个任意带中央子午线即可控制住长度综合变形。这样就避免了重叠带的问题。在不改变投影面高度的情况下,对中央子午线的位置进行推算。分别选取中央子午线为117°09′、117°15′、117°30′进行计算,经计算,中央子午线在117°09′时,既能满足长度综合变形不大于 15 mm/km的技术要求,改正数分布又比较合理。如果改变投影面高度,在对公共区域控制点将发生改变,边长变形比例较差也不一致,而且后续的成果转换也比较复杂、工作量也很大。经研究讨论,在长度综合变形满足规范要求的情况下,考虑与原坐标系的衔接性,决定在满足规范的要求下不改变原投影面高度。
4.3 确定原点位置及坐标加长数
考虑与原坐标系的方向一致性,原点纬度不发生变化,以及考虑到新坐标系下的控制点点位及地形图资料与原资料的相对关系不应交叉,北坐标加长数保持不变,东坐标加长数为20万千米。
4.4 求解新中央子午线下的参数
(1)技术路线
①控制点转换:通过高斯反、正算进行;
②新中央子午线下七参数求取。
(2)采用数学模型
①高斯反算:
②高斯正算:
(3)求取七参数
选取7个控制点,分别在原坐标系及新坐标系下进行计算,计算结果如表2所示。
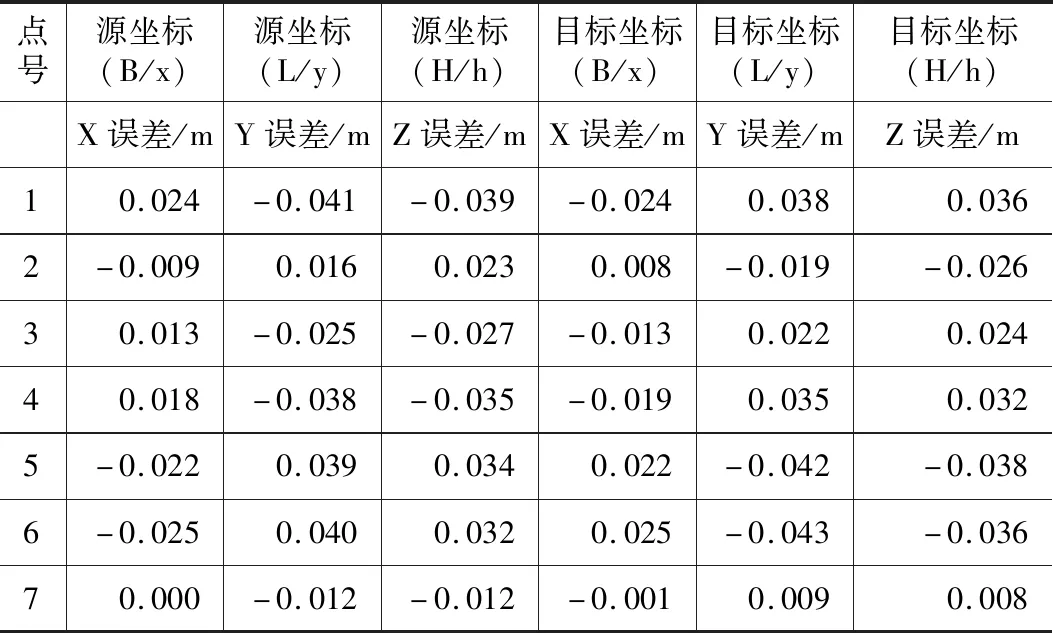
控制点坐标转换残差统计表 表2
残差均在技术要求范围内。
4.5 新坐标系的验证
(1)新坐标系下长度综合变形区域的分析,如表3所示。
新坐标系下长度综合变形计算表 表3
(2)通过求取的参数对周边控制点进行检验,精度达到技术要求,详细情况如表4所示。
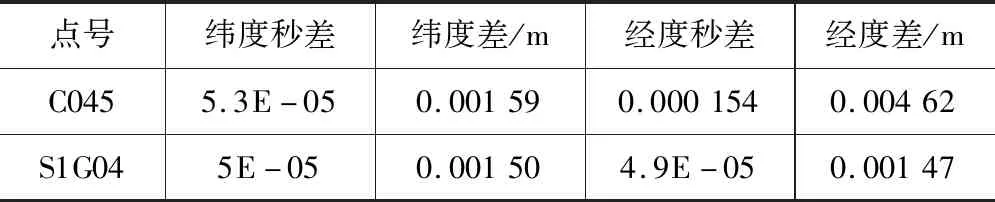
根据参数转换后与已知值的差值表 表4
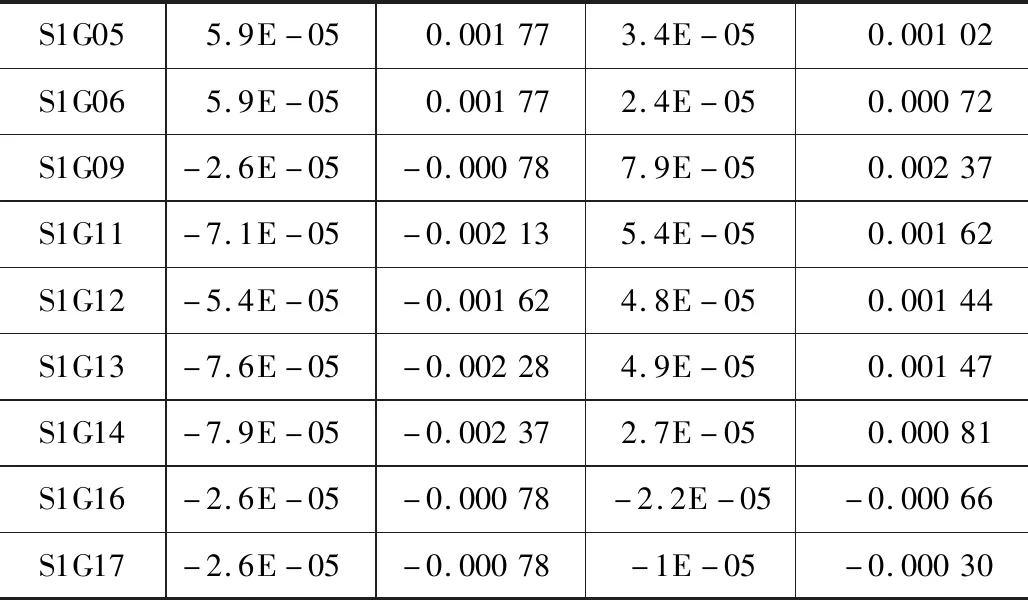
续表4
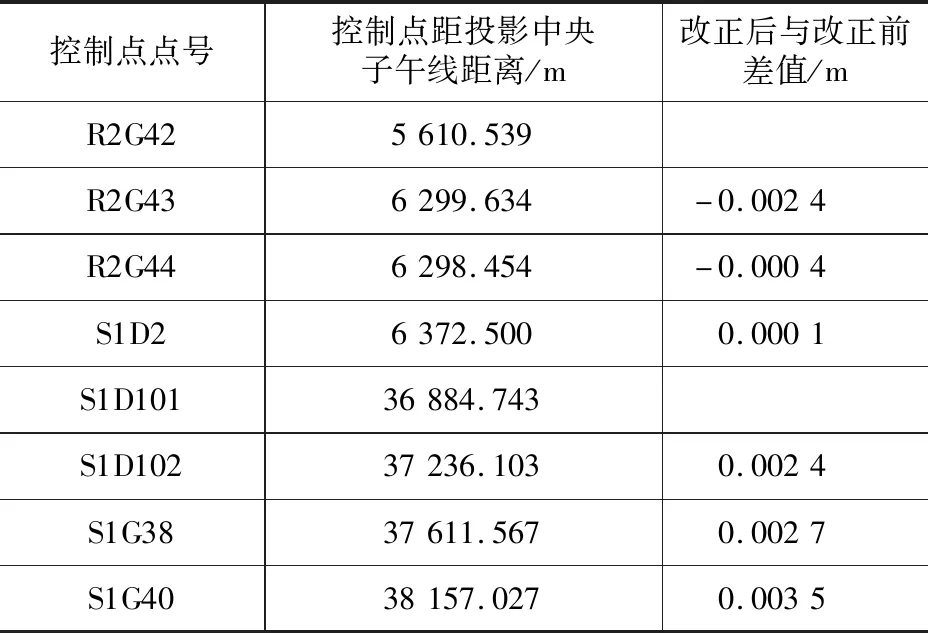
(3)通过已经布设的精密导线控制点边长改正结果均满足规范要求,判定新坐标系的适用性,济南市勘察测绘研究院在线路沿线共布设40个卫星定位控制点,102个精密导线点,经计算182条导线测距边中,长度综合变形最小为0.000,最大为0.011,平均值为0.002。
4.6 和轨道交通R2线济南93坐标衔接情况
轨道交通S1线最西段为轨道R2线,共选取R2G42、R2G43、R2G44三个公共卫星定位控制点。以上三点同时具有117°中央子午线和117°09′中央子午线坐标。经计算,三条边方位角差值均为0,距离差值分别为 3.0 mm、2.5 mm、1.5 mm,相对误差分别为 1/271393、1/256794、1/181917,满足城市轨道交通卫星定位控制网相对中误差1/100000的要求。
5 结 语
本项目研究了原93济南独立坐标系统的建立形式,考虑了与其他轨道交通线路的衔接,并依据转换工作量最小为设计原则,使该坐标系在满足相关技术规范的基础上,在对已有地形图资料、控制点资料、规划元素、土地规划等转换上,做到了长度面积变形最小、无差转换。
本项目的实践和研究为以后济南市城市轨道交通工程坐标系的建立奠定了基础。济南市南北窄、东西长、南北高差大的特点决定了济南市轨道交通建设将会采用一个椭球参数、多个投影带的局面,特别是近期国务院已批复莱芜市整体划入济南市,本项目的研究为同类型的城市轨道交通坐标系建立以及后续其他线路的坐标系建立提供了参考和借鉴。
