用于智能车的棒状像素场景表达方法研究

陈 磊,黄影平,胡 兴,慈文彦

(上海理工大学 光电信息与计算机工程学院,上海 200093)

1 引 言

交通场景理解是智能汽车环境感知系统的基本任务.计算机视觉技术被广泛运用于智能汽车.特别是立体视觉技术所具备的三维重建能力,十分有助于距离测量、物体检测和场景分析等.双目视觉技术中,深度图的应用不仅能够优化图像分割[1],且在多目标检测系统[2]中证明了其有效性.场景理解是识别所有移动和静止的物体,从而确定车辆可能驶入的自由空间,即可通行区域.棒状像素模型[3]是解释交通场景的有效方法之一.通过使用双目相机装置,该方法能够提取障碍物的逐列分段,称之为“棒状像素”.每个棒状像素是一个矩形棒,根据其相对于相机的3D位置而定义,并且直立于地面上,具有一定的高度.自由空间是图像中地平面的一个子集,而棒状像素的存在能够限定这个位置的自由空间边界.棒状像素模型可以实现对各种障碍物的通用检测,大幅降低数据量,为后续处理提供有效的计算结果,是一种紧凑有效3D交通场景表达方法.

Badino等人[3]于2009年首次提出棒状像素模型.其根据立体图像计算随机占据栅格图,获取地平面的自由空间和棒状像素的基点.通过预定义的距离知识将视差图中的前景和背景进行分割,并采用依赖于灰度信息的代价函数来确定前景和背景之间的边界,得到棒状像素的高度.自此,棒状像素模型的计算方法被广泛研究.Pfeiffer等人[4]使用6D-Vision卡尔曼滤波器来估计每个棒状像素的横向和纵向运动,将原始静态棒状像素模型扩展到动态棒状像素模型,帮助检测移动障碍物.基于颜色提示的像素级语义分割和场景的几何特征,增强了棒状像素的估计[5].而卷积神经网络的利用[6]进一步扩展了该方法.Benenson等人[7]和Wieszok等人[8]提出的方法不需要计算深度图,在不获取视差值的条件下,构建尺寸为1个像素的窗口计算代价量,作为RGB颜色通道上的绝对差值之和,直接由立体图像获取棒状像素模型.Benenson等人[7]通过代价量得出平滑约束和先验知识,从而提取棒状像素.Wieszok等人[8]扩展了这一思想,利用颜色模型和代价函数改进地平面和棒状像素的估计.Saleem等人[9]使用共线的三目视觉系统构建棒状像素模型.结合多图融合技术,计算视差空间中的传递性误差,从而提高三张配对的立体图像的视差值一致性,获得鲁棒的棒状像素结果.

棒状像素模型在一些应用中使用并证明了其有效性.Enzweiler等人[10]将3D棒状像素与目标分类的先验知识进行匹配,实现基于棒状像素的目标辨识.Schneider等人[11]通过深度学习的场景标记方法将深度棒状像素扩展为语义级棒状像素,从而为每个像素提供一个对象类标签.Cordts等人[12]将棒状像素与图像语义分割相结合,进一步增强场景理解.Erbs等人[13]使用动态棒状像素模型来检测和跟踪交通场景中的运动物体.通过在线颜色建模来分割道路和障碍物,可以进一步增强棒状像素模型的场景表示[14,15].

本文扩展了Badino[3]的工作,利用U视差的性质提出了一种新颖简单的棒状像素估计方法.该方法可以规避某些区域的视差模糊及丢失带来的误差,准确标记出场景中的移动或静止的前景障碍物平面,获取多种地形环境下的自由空间,有效表达交通场景.

2 基本原理

2.1 立体视觉原理

双目立体视觉是从两个不同的位置观察物体,从而提取物体的三维信息.图1显示了立体相机的安装方法和相机坐标系与世界坐标系之间的关系.两个相同的相机校正后保持光轴平行安装在车辆上,它们的光心是Ol和Or,水平轴平行于地平面.两个相机坐标系分别是(Xl,Yl,Zl)和(Xr,Yr,Zr),坐标原点位于图像的中心.在此模型中,世界坐标系(X,Y,Z)设置与左相机的坐标系重合.

图1 理想的双目立体视觉模型Fig.1 Model of an ideal binocular stereovision

对于场景中的点P(X,Y,Z),将其投影到左图和右图以分别获得Pl(Xl,Yl)和Pr(Xr,Yr).根据几何关系,可以得到式(1):

(1)

那么P点的世界坐标可以计算出来:

(2)

其中,f是相机焦距,b是基线距离.d是视差值,由以下等式表示:

d=xl-xr

(3)

因此,只要计算图像中的每个点的视差值,便可以获得场景的三维信息.通过立体匹配算法可以获得浓密视差图,存储实际场景中每个点的视差值,便可将图像中所有视差非零点的三维信息恢复到世界坐标系中.

2.2 U视差原理

Labayrade首次提出V视差[16]的概念,U视差的原理与之类似.浓密视差图由立体图像对获得,将其表示为δ(u,v),其中1≤u≤Ncol,1≤v≤Nrow.设H是图像变量δ的函数,使得δu=H(δ),将δu(u,d)称为“U视差图”.H在给定图像的列上累计相同视差的点,对于图像列u,δu(u,d)中点的值是该列上具有相同视差d的点的数量,即:

δu(u,d)=card{u:1≤u≤Ncol∩INT(δ(u,v))=d}

(4)

其中,0≤d≤dmax,表示视差图δ(u,v)中量化后的视差范围;INT是取整函数.δu(u,d)的横坐标u与δ(u,v)的横坐标是同一个变量,δu(u,d)的纵坐标是视差d.

在实际场景中,可以将相机前方的障碍物平面简化为两类:垂直正平面和垂直侧平面.如图2所示,左相机坐标系(Xl,Yl,Zl)和右相机坐标系(Xr,Yr,Zr)构成双目立体视觉系统.为了简化问题,将世界坐标系的原点设置在两个相机坐标系原点的中心,其Z轴平行于水平面,θ是相机光轴与水平面的俯仰角.相机拍照成像时,图像中点的位置由图像坐标系(u,v)描述.相机光心投影在图像平面的中心点,坐标是(u0,v0).

根据Hu[17]等人的工作,此模型下世界坐标系与图像坐标系的转换等式为:

(5)

根据式(3)可以推导出视差的计算等式:

(6)

在世界坐标系中,垂直正平面可以描述为:

Z=p

(7)

当θ很小近似于0°时,可认为该面上每个点到相机的距离均为p,结合U视差原理与式(6)可推导出该障碍物平面在U视差图中的方程:

(8)

式(8)表明垂直正平面在U视差图中呈现为一条水平直线.

世界坐标系中得垂直侧平面可以描述为:

Z=ρX+τ

(9)

结合式(5)(6),可推导出对应于立体图片中左图的方程:

(10)

当俯仰角θ足够小时,等式(10)可简化成:

(11)

上式表明垂直侧平面在U视差图中近似表现为一条斜线.

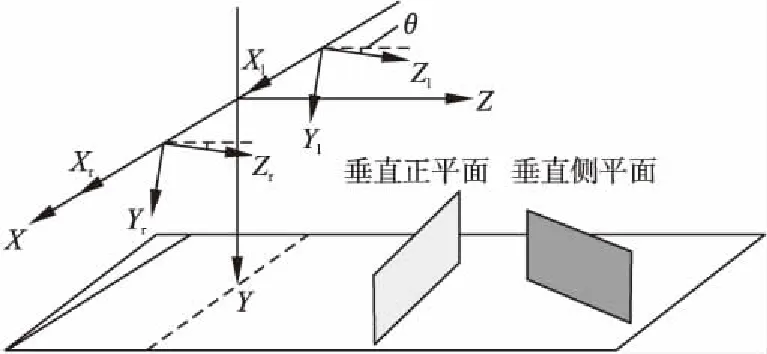
图2 世界坐标系下的两种障碍物平面Fig.2 Two planes of obstacles in world coordinate system

3 棒状像素模型的建立

当棒状像素模型被用于描述立体场景时,各个方向上最靠近自车的障碍物被标记为感兴趣的对象,即棒状像素,其背后的物体被视为背景.自由空间是地面上不包含任何障碍物的区域,即自车可以驶入的区域.一旦某位置的棒状像素被确定,它的存在即可排除该位置的自由空间,因此,自由空间与棒状像素的计算是密切相关的.对于构建棒状像素模型,其主要任务是将棒状像素从地面和背景中区分出来,并确定它们的高度和距离.本文提出的棒状像素估计方法利用U视差图的属性来完成这些任务.

3.1 U视差图的形成及与场景中各类平面的关系

在驾驶环境下,场景中的对象可以被分为两类.第一类是路面,可以抽象为水平面;第二类是近似垂直于地面的障碍物,包括车辆、行人、树木和路边建筑,可以抽象为垂直平面.这些平面在U视差图中具有不同的表现形式.

对于水平平面,由于水平面(道路平面)的覆盖区域由近至远且范围较大,所以它的视差累积点被分散,即δu(u,d)很小.因此,水平面将离散分布在U视差图中.

对于两种垂直平面,已经在2.2节中作了具体推导.实际场景中,垂直正平面包括汽车正车身、行人和树木等对象,路边建筑、墙面、汽车侧车身等则被认为是垂直侧平面.由于垂直正平面上的点到我方车辆的距离近似相等,即U视差图中该平面的对应点具有相同的视差,因此它在U视差图中显示为水平线段,并且线段的长度表示平面宽度.类似地,U视差图中垂直侧平面对应点的视差值是沿横轴连续变化的,因此它在U视差图中显示为近似斜线段.障碍物的距离取决于其视差,视差越大,障碍物越近.通过在U视差图中检测这些线,障碍物的位置及尺寸能够被确定.

此处以一个典型的交通场景作为示例,图3(a)是这个场景的左图.本文使用Geiger提出的立体匹配算法[18]来生成浓密视差图,该算法可以实现高分辨率图像的快速匹配,并且无需全局优化即可产生精确的浓密重建结果.结果如图3(b)所示.最终生成的U视差图如图3(c)所示,其中3D障碍物呈现为水平或倾斜线段,路面则分散在图中且不能被清楚地观察到.

3.2 地面与背景的剔除

由于地面相关点具有小的灰度并且离散地分布在U视差图中,因此可以通过设置合适的灰度阈值将它们去除,图4(a)是去除了地面相关点并且二值化后的U视差图.将图4(a)与图3(c)进行比较,可以观察到只有障碍物信息被保存下来,呈现为水平线段和斜线段.另外,该步骤消除了一些具有偏差视差的离散点,从而使距离估计更准确.

图3 U视差图的构建Fig.3 Construction of U-disparity map

图4(a)中点群的位置反映了它与相机的距离,位置越低则距离越近.为了去除背景障碍物,可以简单地保留较低点并丢弃同一列上的较高点.然而,在实际交通场景中,某些障碍物可能含有缺乏纹理的区域,导致浓密视差图中部分点的视差丢失.那么,图4(a)中对应于该障碍物的线段则会不连续或中断.因此,不在图4(a)中进行背景剔除,而是通过以下转换来生成压缩的U视差图,从而规避这一影响.

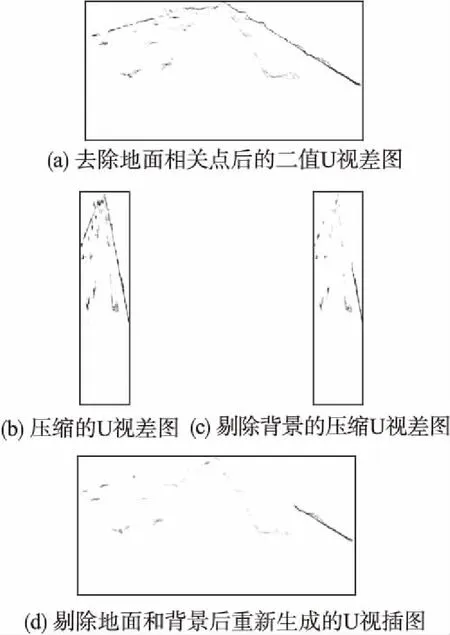
图4 地面点与背景点的剔除Fig.4 Elimination of ground points and background points

图4(a)被分成多个宽度为w的小矩形,将U视差图横向压缩成图4(b).压缩的U视差图可以写成式(12)的形式:

(12)

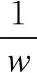
然后,对图4(b)中每列的点从下到上进行遍历.当连续搜索到具有非零值的点时,将其视为前景对象并保留下来,同时将其上方的点作为背景点丢弃.结果如图4(c)所示.

根据式(13)的转换关系,将去除背景后的压缩U视差图重新转换为U视差图:

(13)

式中Q是重新生成的U 视差图,s和t分别是Q的横坐标和纵坐标.T是去除背景的压缩U视差图,即图4(c).重新生成的U视差图如图4(d)所示.

3.3 基点与顶点的提取

图4(d)所示的U视差图仅包含前景障碍物的相关点,而其他点均被移除.因此,将图4(d)投影回浓密视差图能够提取前景障碍物的基点和顶点.

U视差图中的任意一个点都是从对应的视差图中的一个或多个点计算得到的,我们将视差图中的这些点称为“贡献点”.反过来,视差图中的任意一个点均对应于U视差图中的唯一点.该映射关系可以在图5中描述为三维到三维的空间映射.在图5中,I1是三维U视差图,I2是与之对应的三维视差图.I1和I2具有相同的横坐标(U).I1中的垂直坐标(D)是视差值,而I2中的垂直坐标(V)是图像行数.I1中的第三坐标(N)表示同一列中具有相同视差的点的数量,而I2中的第三坐标(D)与I1中的纵坐标相同.横坐标和垂直坐标定义位置,而第三坐标表示图像的灰度值.I1中的坐标系(U,D,N)可以描述为以下函数:

N=Φ(U,D)

(14)

I2中的坐标系(U,V,D)可以表示为:

D=Δ(U,V)

(15)

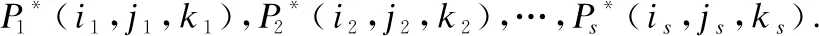
(16)

在I2的第a列中搜索视差为b的点,便可以确定未知数{j1,j2,…,js}.因此,可以获得贡献点P*1(a,j1,b),P*2(a,j2,b),…,P*s(a,jc,b).对应地,视差图中的点P1(a,j1),P2(a,j2),…,Pc(a,jc)可以被确定.

将图4(d)映射到浓密视差图后得到图6,可以注意到部分障碍物点群内部含有少量空洞.这是由于将点群从U视差空间映射到视差图时,视差的匹配搜索使得一些视差错误点无法被匹配到,从而被剔除,保证了视差的准确性,有利于后续步骤的距离估计.

图5 U视差图到视差图的映射Fig.5 Mapping from U-disparity map to disparity map

图6中地面相关点和背景相关点全部被消除,仅保留前景障碍物,可以直接在图中提取基点和背景边界.如图7所示是原始场景图中标记出的前景障碍物基点和顶点.

图6 视差图中被投影的贡献点Fig.6 Projected contribution points in the disparity map

3.4 棒状像素的提取与距离估计

当图像中每列的基点和顶点被计算出来,就可以直接提取棒状像素.如果棒状像素的预定义宽度大于一列,则将前一步骤中获得的多列高度值融合起来,得到棒状像素的高度.

图7 基点与顶点Fig.7 Base and top-points

棒状像素的距离根据其中所有贡献点的主要距离来进行估计.由于在构建棒状像素模型时,偏差点已经被去除,因此每个贡献点均具有准确的视差值.图8示出了棒状像素以及对应的自由空间,棒状像素的灰度代表距离信息.

图8 棒状像素模型Fig.8 Stixel World

4 实验分析

4.1 实验结果

算法在配置1.6GHz的四核英特尔i5处理器和8GB内存的计算机中运行.从KITTI公共数据集[19]中选择City、Road、Residential和Campus等场景类别的图像序列作为实验数据,图像分辨率为1240×375像素.取棒状像素宽度为10个像素,得到棒状像素和自由空间的结果如图9所示,棒状像素的灰度值呈现了距离信息.

图9 不同场景下实验结果Fig.9 Experimental results in different scenarios

4.2 性能评估及比较

本文的重点是棒状像素边界的准确提取而不是距离测量,距离估计的准确性取决于立体匹配算法[18].将检测到的基点、顶点与手动标记的真实值进行比较,通过棒状像素的位置误差来评估算法.每帧图像的基点均方根误差以及顶点均方根误差分别通过式(17)(18)进行计算:

(17)

(18)

其中,Nstx表示图像中棒状像素的数量,Bi和Ti分别是检测得到的基点位置和顶点位置,bi和ti分别表示基点位置和顶点位置的真实值,基点和顶点的位置值以像素为单位.从不同类别的场景中各选择100帧图像,对本文算法和传统算法[3]分别进行实验.根据式(17)、(18)计算每帧图像的基点误差和顶点误差,从而得出不同场景下的平均误差,以此来比较两种算法准确性.

在表1和表2中,分别展示了各个图片序列的平均基点误差和平均顶点误差.比较两种算法可见,本文的算法较传统算法的在基点与顶点的提取精度上有提高.

表1 与传统方法的基点误差比较
Table 1 Comparison of base-point error

图片序列基点误差(像素)本文算法传统算法City2.84.2Road6.37.7Residential2.93.1Campus4.87.4

在实际应用中,算法的计算效率也是衡量其性能的重要因素之一.基于立体视觉的棒状像素提取方法中,立体匹配是其中的一个关键环节.不同的立体匹配算法,其准确度和计算耗时有较大差异.由于本文方法与传统方法采用的的立体匹配算法不同,而本文与传统方法的主要不同在于棒状像素的提取方法不同,所以实验仅对棒状像素的计算时间进行比较,来对比两种方法的运行效率.

表2 与传统方法的顶点误差比较
Table 2 Comparison of top-point error

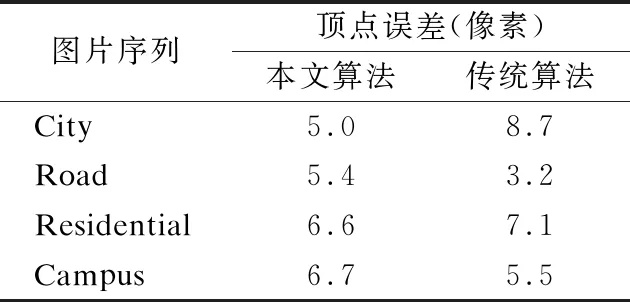
图片序列顶点误差(像素)本文算法传统算法City5.08.7Road5.43.2Residential6.67.1Campus6.75.5

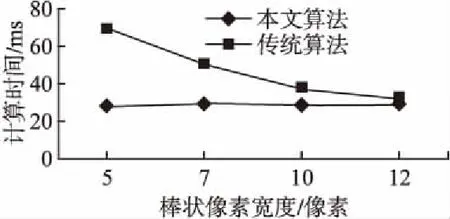
图10 棒状像素计算时间比较Fig.10 Comparison of stixel computation time

在实验中,对棒状像素取不同的宽度,统计平均的计算时间,结果如图10所示.取棒状像素宽度为12个像素时,两种算法运行时间比较接近;随着棒状像素宽度的减小,传统算法的计算时间呈递增趋势,而本文算法的计算时间则保持稳定.考虑到实际应用中的精度要求,棒状像素的宽度一般不超过10个像素.由此可看出,本文提出的算法相较传统算法减少了计算时间,提高了运行效率.

构建棒状像素的传统算法与本文算法均基于深度信息,Benenson等人[7]提出的算法直接对立体图片进行计算,不需要获取视差图.将本方法的结果与该算法的结果进行比较.采用文献[7]的评估方法:对于一个给定的像素偏离误差,统计图像中低于该误差的棒状像素的数量占比,作为得分来评估算法,高分值说明性能好.图11给出了棒状像素的基点及顶点的比较结果.如图11(a)所示,本文算法提取基点的精度较Benenson算法有一定的提升;由图11(b)可见,当给定的误差小于20像素时,本文算法提取顶点具有优势;大于该值时,Benenson算法提取顶点稍微好一些.

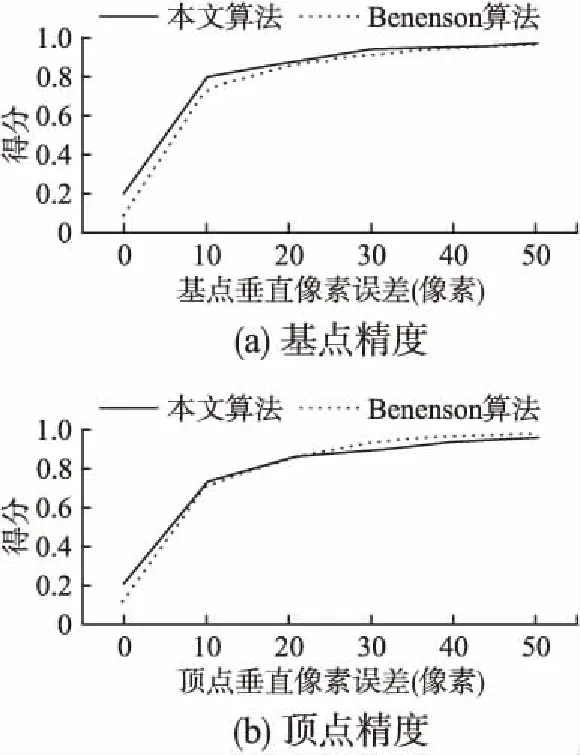
图11 与Benenson方法的棒状像素精度比较Fig.11 Comparison of stixel accuracy with benenson method

4.3 实验结果分析

1)对于1240×375分辨率的图像,单帧图像的棒状像素均方根误差在10个像素以内,较传统算法和Benenson算法都有一定的提高.

同时,算法在计算速度方面有所提升.由于本算法对基点和顶点进行整体投影和提取,棒状像素个数的变化并不影响计算效率.当棒状像素宽度为5、7、10个像素时,相比传统算法,棒状像素的计算时间分别减少了59%、40%、22%.

2)本算法的适用场合并不局限于平坦道路.图9(b)中展示了轻度上坡路面的棒状像素提取结果,图9(c)显示了坑洼路面的计算结果.从实验可以看出,本算法能够识别前景障碍物并为场景生成准确的棒状像素模型.

3)场景图像的像素点达到105数量级.计算并定义每个像素点,对系统的计算能力是一个巨大的挑战.在本方法中,只需要少量的包含距离和位置信息的棒状像素便能够表达交通场景,大幅减少了计算开销,简化了场景的分析过程.

5 结 论

本文利用U视差的性质,提出了一种新颖简单的棒状像素估计方法.U视差图中障碍物相关点呈现为水平或倾斜线段,而地面相关点分散地分布在U视差图中.通过灰度阈值化处理消除地面相关点,根据距离信息去除背景障碍物.得到的U视差图仅包含前景障碍物相关点,将其投影回视差图进行匹配,从而确定前景障碍物的基点和顶点,提取棒状像素.实验结果表明,该方法可以有效地构建多种场景的棒状像素模型.

与现有的棒状像素估计算法相比,这项工作的贡献可以总结如下:

1)现有算法[3]采用基于灰度的代价函数并结合预定义的距离阈值来分割前景和背景.本文提出的方法直接在U视差图中去除背景和地面相关点,将所得的U视差图重新投影回视差图来提取图像每列的基点和顶点.

2)提出的方法不需要对地平面进行建模,因此,它不受地形的约束.无论是在倾斜路面或是在坑洼路面上,算法都能正常工作.

3)立体匹配算法的局限性可能会导致视差图存在视差错误或丢失的情况.本文的方法中,地面相关点的去除以及压缩U视差图中对数据的模块化处理,有利于规避这一误差.

4)算法在保证低误差的同时,提升了运行速度.

本算法准确性受到视差图精度的局限,且大部分计算时间消耗于视差图的生成.在今后工作中,开发出高精度、高实时性的立体匹配算法,是进一步提升性能的关键.