基于正交试验法的模锻模具磨损分析及优化

蔡力钢， 刘海东， 程 强， 刘志峰， 杨聪彬， 亓 寅

(1. 北京工业大学先进制造技术北京市重点实验室， 北京 100124；2.鹰潭应用工程学校加工制造学部， 江西 鹰潭 335000)

近年来，随着军工产业的不断发展，模锻工艺在航空工业领域[1]有着非常广阔的应用前景，并且在重工业生产中占据了重要的位置. 模锻过程中，模具的失效形式[2]比较复杂，大多数的失效情形是由于模具产生塑性变形、模具磨损严重、模具产生断裂等因素造成的. 在实际生产中，由于模具严重磨损而导致模具失效的情形占总模具失效形式的70%. 因此模具磨损成为影响模具寿命最主要的因素，同时也体现了模锻工艺的优劣性[3]：较小的模具磨损不仅可以有效减少材料的损耗，还可以提升锻件产品的尺寸精度和模锻工艺的稳定性. 而当模具磨损量超过工艺要求的临界值之后，模具会因为失效[4]而大幅降低了锻件产品的生产质量，同时还会影响到产品的生产成本[5]. 因此如何减小模具磨损成为了模锻生产中的重要难题.

国内外的许多学者在研究模具磨损[6]方向取得了一些成果：周杰等[7]从模具硬度和初始温度的角度研究了一次模锻成型过程中模具磨损的影响规律. 王雷刚等[8]根据修正的Archard磨损模型，通过有限元软件对模具的磨损状况进行了仿真分析；史双喜等[9]基于Archard磨损理论研究了精冲模具的相关磨损规律；Lee等[10]基于Archard磨损模型，同时考虑到锻压温度对模具磨损的影响，提出了相适应的修正模型. Eriksen等[11]将模锻工艺中的模具结构进行了相关优化，以此来降低模具磨损程度；Painter等[12]通过仿真分析对热挤压过程中的磨损状况进行了相关研究；Kang等[13]研究了模具硬度与模具磨损量之间的关系.

目前，在实际生产中，通过试验的方法对模具磨损深度和模锻工艺参数之间的关系进行研究需要耗费大量的经济成本，所以本文借助Deform软件对不同工艺参数组合的模锻过程进行有限元仿真分析，通过仿真试验来研究工艺参数对模具磨损的影响. 首先根据Archard摩擦理论进行推导分析，建立适用于热模锻工艺的模具磨损修正模型，再通过该磨损模型预测出对模锻工艺中模具磨损深度影响较大的工艺参数. 将这些关键的工艺参数作为因素，分别取不同的4个水平来进行正交试验设计. 通过较少的仿真试验次数得到模锻工艺参数的最优解. 同时利用多项式拟合法和极差分析法对仿真试验结果进行数据处理，通过比较不同工艺参数下的极差值，来获得对模具磨损程度影响最大的工艺参数.

1 模锻磨损模型的建立

1.1 Archard理论简介

由于工艺参数设置的不同，会导致模锻成型过程中的温度、等效应力分布、金属流动速度等结果也发生相应的变化，因此工艺参数的设置可以间接地影响模具磨损情况. 在实际生产中，可以考虑将这些工艺参数进行组合设置，构造出一个模锻工艺参数与模具磨损深度的理论模型. 在Archard磨损模型[14]中，一般情况下磨损率能表示成如下函数模型：

(1)

(2)

式中：V是磨损体积；K是磨损系数，普通钢材料的K取值范围为10-2～10-7；p是坯料和模具接触表面的法向压力；l是模具和坯料之间的相对位移；Δt是磨损过程中的接触时间；Hm是模具硬度；v是坯料的变形速度.

1.2 建立模具磨损修正模型

将Archard磨损模型进行数学研究，推导出一个适用于热模锻成型过程中模具磨损量的计算公式. 由于热模锻成型过程中会造成温升，因此温度对模锻成型过程的影响也应该考虑在内. 随着模锻工艺中的实际温度不断上升，坯料的硬度会降低，坯料的流动抗力也会下降，同时模具硬度也会下降. 而在热模锻成型过程中，温度T的变化与时间t有关，所以磨损体积V、模具承受的压力p、模具和坯料之间的相对位移l就都可以表示为时间t的函数

(3)

式中：W是模具磨损深度；A是坯料和模具之间的接触面积；σn是坯料的应力值；v是坯料的变形速度；t是滑移时间. 根据式(3)推导出模具磨损的修正模型

(4)

式中：s是模具的位移；t是模具移动的时间. 所以σn(s,t)、v(s,t)、Hm(s,t)分别表示模具在某一时刻处于某一位置下的应力值、变形速度和模具硬度. 在式(4)磨损模型中，坯料所产生的应力值σn被默认为常量. 但是在实际的模锻成型过程中，坯料和模具之间不存在绝对光滑的接触面，所以实际的应力大小和模锻过程中模具接触面的磨损深度相关，坯料所产生的应力值也会随着模具接触面上不同位置的磨损深度不同而产生相应的变化，进而模具上的磨损情况也会改变. 针对以上问题，需要在Archard磨损模型的基础上建立适用于实际模锻生产情况的修正模型.

根据有限元运算可以得出在某个确定的时刻，上模移动至某个确定位置后的σn与v，因此可以求出模锻成型过程中某一时刻的模具磨损量. 将式(4)通过积分就能推导出

(5)

把式(5)进行数值模拟运算，能计算出在热模锻工艺中一段时间内的模具磨损量，再将热模锻工艺中的模具磨损状况进行仿真分析，就能建立模锻工艺参数与模具的最大磨损量之间的函数模型

Wmax=f(v,T,εF,m)

(6)

式中：Wmax是模锻过程的最大模具磨损量；v是坯料的变形速度；T是坯料的变形温度；εF是坯料的变形程度；m是坯料和模具之间的摩擦因子. 根据这个新建立的模具磨损修正模型可知，影响模具磨损的因素包括变形速度v、变形温度T、变形程度εF和摩擦因子m. 如果忽略不同坯料材料、模具材料本身的性质区别，只考虑工艺参数对模具磨损的影响，那么变形速度v、变形温度T、变形程度εF相对应的工艺参数就是坯料的初始温度、模具的初始温度和上模的打击速度. 即这3个工艺参数就是对热模锻成型过程中的模具磨损量有较大影响的3个不同因素.

将式(5)中的σn和v根据有限元模拟的数学方法，对材料与模具之间的接触面采用离散化分析[15]：将一段时间Δt作为间隔，该间隔内，σn可以被认为是不变的，进而得出在该间隔Δt中模具的某个接触点的某次磨损深度，最后可以计算出在这段时间中整个模具的磨损深度，即推导出

(7)

式中：M为总时间步数；N为接触面的总结点数；Δt为时间步；H为模具硬度. 而σn与v的值都能根据有限元计算来得到. 所以，在k和H固定不变的情况下，就能通过数值模拟的方法计算出一次热模锻成型过程中模具和材料接触面的磨损量，即可通过有限元模拟计算出热模锻工艺过程中的模具磨损深度. 图1所示为本文中模锻工艺参数优化方法的流程框图.

2 正交试验法的应用

2.1 基于模锻工艺的正交试验设计

正交试验设计[16]是研究多因素多水平的一种高效率的试验设计方法，对于模锻模具磨损而言，坯料的初始温度、模具的初始温度和上模的打击速度是可控对象，并且根据热模锻模具磨损修正模型，这3个关键性工艺参数对模锻成型过程中的模具磨损影响十分显著，所以本文将这3个关键性工艺参数进行三因素四水平的正交试验设计.

本试验采用L16(43)的正交表，即将坯料的初始温度、模具的初始温度和上模的打击速度作为3个试验因素，在每个因素下面找到4个水平的数值，一共进行16组试验，用Deform软件仿真分析每一组试验结果所得出的模具磨损深度，最后推导出使模具磨损深度实现最小值的最佳工艺参数.

根据本试验实际生产的工艺要求：初始坯料的温度范围是900～1 200 ℃，初始模具的温度范围是250～400 ℃，上模打击速度的范围是300～600 mm/s. 可以把初始坯料温度、初始模具温度和上模打击速度作为3个因素，并且按照表1来划分为4个水平. 即坯料的初始温度分别为900、1 000、1 100、1 200 ℃，模具的初始温度分别为250、300、350、400 ℃，上模打击速度分别为300、400、500、600 mm/s. 即得到实际模锻工艺的因素水平表(见表1).

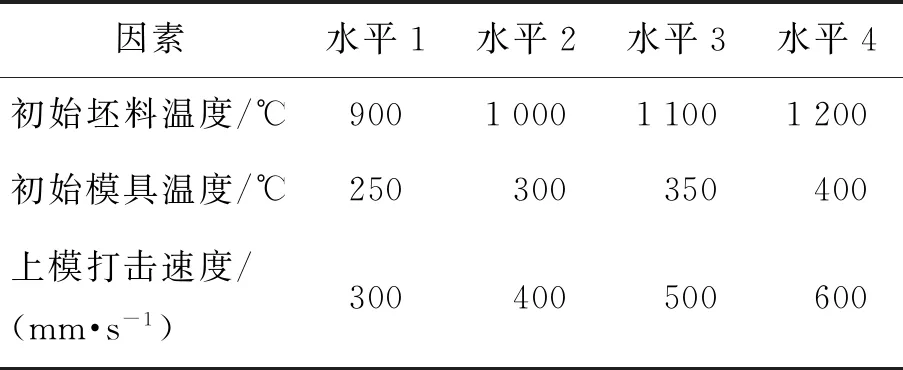
表1 因素水平表

依照表1划分好的因素和水平构建一个三因素四水平的正交试验设计，所选取的正交表为L16(43)，得到基于模锻工艺参数的模具磨损量的正交试验方案，见表2.

对表2进行五阶多项式的数据拟合处理，得到正交试验数据拟合曲线图，如图2所示. 本次试验拟合曲线方程为：y=7.004 1×10-7x5-2.962 7×10-5x4+0.000 456 62x3-0.003 105x2+0.007 875 6x+0.020 956，由图可知，当x=14时，该拟合曲线有极小值为0.013 8. 所以发现试验14所得出的模具磨损深度最小，仅为0.013 8 mm，该模具磨损深度与试验2相比，磨损量减小了53.7%. 所以可以推导出，本次试验的最佳模锻工艺参数是：坯料的初始温度为1 200 ℃，模具的初始温度为300 ℃，上模的打击速度为500 mm/s.

2.2 极差分析法

由于正交表具有综合可比性，因此能用一种更为高效的极差分析法[17]来对整个试验结果进行数据分析. 根据极差分析法的定义可以推导出

(8)

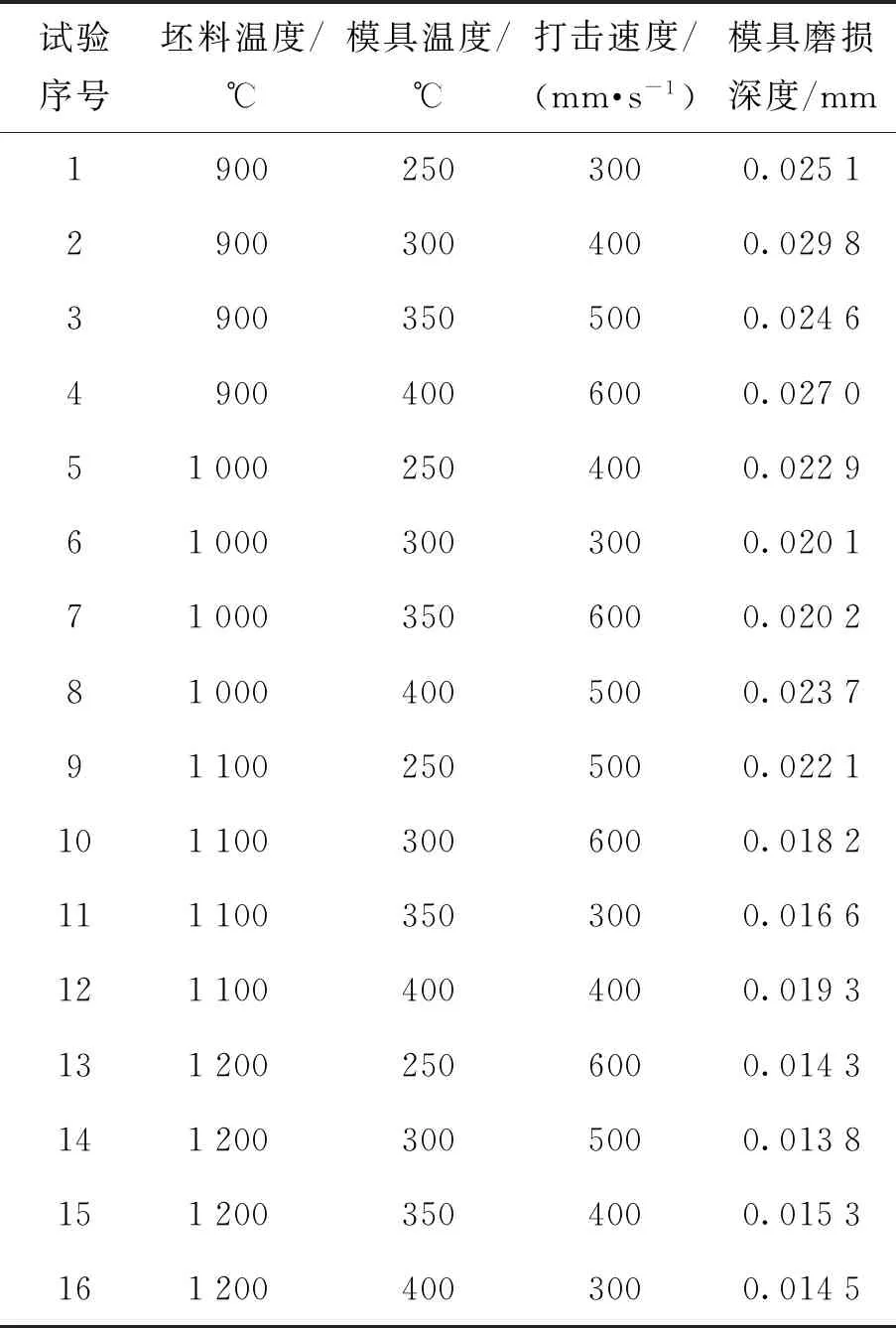
表2 正交试验方案

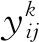
从式(8)可知：Mij为第j因素中所有第i水平的试验结果的平均值，因此就可以推导出极差Rj的公式为

Rj=max(Mij)-min(Mij)

(9)

极差分析法是正交试验设计中很重要的数据处理方法之一，可以分析出第j因素对试验结果的影响程度. 在一次正交试验中，某一个因素极差值的大小和该因素对试验结果的影响程度呈现正比关系.

通过对表2进行极差分析得到表3数据分析结果. 由于R1远远大于R2和R3，且R3略大于R2，因此初始坯料温度对热模锻工艺中的模具磨损的影响最大，上模打击速度和初始模具温度对模具磨损的影响都比较小，且两者对模具磨损的影响程度相差不多，都远远小于初始坯料温度对模具磨损的影响程度.

表3 数据分析结果

3 有限元仿真试验

3.1 有限元模拟在模锻工艺中的应用

在模锻生产中，坯料会产生很大的塑性变形，其实际位移和应力应变存在着非线性关系，通过对模锻加工进行有限元模拟，可以提前预测出整个加工过程的模具磨损量，通过仿真试验结果来推导出本次模锻过程中的最优工艺参数，进而可以在实际生产中提高模具的使用寿命，减小企业的生产成本.

3.2 有限元模型的建立

本次试验选用的是一种航空领域的基本锻件:紧固接头，在航空模锻工艺中具有一定的典型性. 首先采用SolidWorks软件构建本次模锻工艺中所需要的上模、下模和坯料模型，然后导入到有限元仿真软件Deform里面，得到所需要的有限元仿真模型[18-19]. 在Deform中进行相关的工艺参数设置. 单位制选择SI(国际单位制)，坯料设置为塑性体，模具设置为刚性体. 坯料材料采用40CrNiMoA，其对应的国际钢号为AISI- 4340，模具材料采用5CrNiMo，其对应的国际钢号为AISI- L6，初始坯料温度范围是900～1 200 ℃，初始模具温度范围是250～400 ℃，上模运动速度范围是300～600 mm/s，上模的运动方向选择为-z方向，下模处于静止状态. 坯料和模具的摩擦方式设置为剪切摩擦，热摩擦因数设置为0.7，热传导系数设置为11. 热传递的边界条件[20]设置在上下模具和坯料的接触面上. 将Deform软件中前处理的所有基本设置全部完成后，开始运行模拟仿真，等待后处理的实验结果.

3.3 有限元仿真试验结果

在Deform模拟仿真过程中，模锻成型过程分为2个阶段. 第1阶段：上模开始向下运动，但是还没有接触到坯料，所以此时只存在热交换，而没有产生形变. 所以在第1阶段中，只有模具和坯料的温度会发生变化. 第2阶段：上模和坯料开始接触，此时，模具和坯料之间不仅存在热交换，而且坯料同时也发生塑性变形，坯料和模具的摩擦方式为剪切摩擦，材料逐渐填充到模具的腔体中，锻件也开始逐渐成型，图3所示为本实验模锻加工后的锻件成型情况.

用Deform软件依照正交试验方案对模锻成型过程进行16次仿真试验分析，从Deform软件的后处理界面中观察模具的磨损情况，进而得出不同工艺参数组合条件下的模具磨损深度. 由于在整个模锻成型过程中，上模和下模的模具磨损深度并不相同，为了最大化地减小模锻工艺中的模具磨损，从每次仿真试验得到的上模磨损深度和下模磨损深度中取较大值并进行记录. 图4～11所示的是部分仿真试验的模具磨损情况.

3.4 现场试验验证

在现场试验中采用本文所推导出的模锻工艺参数最优解来进行相关工艺参数的设置，即在现场试验中，把坯料的初始温度设置为1 200 ℃，模具的初始温度设置为300 ℃，上模的打击速度设置为500 mm/s来进行实际的模锻试验，图12所示为现场试验中锻件成型图，成型结果和充型效果与仿真结果相同，经测量所得到模具的实际磨损深度仅为0.014 1 mm. 采用本文改进后的模锻工艺参数最优解所得到的模具实际磨损量与仿真试验的理论最佳磨损量之间误差仅为0.000 3 mm，因此本文所提出的模锻工艺参数优化方法对于热模锻成型过程中的工艺参数设置有一定的实际指导作用.

4 结论

1) 在Archard磨损模型的基础上，提出了一种适用于热模锻工艺的模具磨损修正模型，并且进一步推导出对模锻模具磨损影响最大的3个工艺参数：坯料的初始温度、模具的初始温度、上模的打击速度.

2) 根据关键性工艺参数的正交试验设计，建立了一套减小模锻模具磨损的工艺规则，该工艺规则可以根据实际生产中的不同工艺要求来推导相匹配的工艺参数最优解，在实际模锻过程中实现模具磨损量的最小化.

3) 根据极差分析法所得到的数据处理结果，发现在模锻工艺中，各个工艺参数对模锻模具磨损的影响程度按照从大到小的顺序排列依次为：初始坯料温度、上模打击速度、初始模具温度.

4) 通过多项式拟合法得到基于模具磨损的模锻工艺参数最优解：在坯料的初始温度为1 200 ℃，模具的初始温度为300 ℃，上模的打击速度为500 mm/s时，模锻过程中的模具磨损量达到最小值，仅为0.013 8 mm. 该模具磨损深度与试验2结果相比，磨损量减小了53.7%.