TBM滚刀破岩过程的声发射特征

2020-01-14龚秋明丁世鹏殷丽君

北京工业大学学报 2020年1期

龚秋明，丁世鹏，吴帆，殷丽君

(北京工业大学城市防灾与减灾教育部重点实验室，北京 100124)

在地下空间大开发的今天，隧道掘进机(tunnel boring machine，TBM)以其快速、高效、安全、环境友好和围岩扰动小等优点，在地下工程建设中得到广泛应用[1]. TBM破岩依赖于滚刀与岩石之间的相互作用，在滚刀侵入作用下岩石内部产生损伤裂纹，相邻裂纹扩展贯通便形成岩片脱落，达到破岩的目的[2]. 在滚刀与岩石的作用过程中，可通过分析滚刀三向力、岩石损伤裂纹和岩片尺寸等特征来了解滚刀与岩石间作用规律，从而提高破岩效率. 国内外学者在这方面已开展大量研究.

文献[3-7]分别利用不同破岩平台进行线性切割试验，对比分析滚刀力、切割系数和比能值等参数，研究不同刀盘滚刀间距和贯入度对破岩效率的影响. 马洪素等[8]在围压对TBM滚刀破岩影响研究中，分析滚刀三向力、比能以及岩体可掘性指数等特征. 姚羲和等[9]通过对裂纹进行数字化处理，研究花岗岩在滚刀单次和多次贯入切割作用下的破裂模式. Entacher等[10]在小尺寸线性切割试验后，用荧光剂对裂纹进行标记研究. 龚秋明等[11]在线性切割破岩试验后，称重并测量岩石碴片，通过碴片的粗糙度指数、长轴长度和扁平度等特征来反映滚刀破岩效率.

不少学者已利用声发射研究了岩石在单轴、三轴压缩、巴西劈裂以及压头侵入等试验中的破裂过程. 文献[12-14]通过分析单轴压缩试验中声发射事件数，事件率与应力、时间的关系，研究岩石破坏的全过程. 赵兴东等[15-16]利用声发射定位给出单轴压缩条件下岩石内部裂纹的空间演化过程. 杨永杰等[17]和Zhang等[18]在三轴压缩试验中利用声发射技术研究围压对岩石破坏的影响. 文献[19-20]研究拉伸、劈裂和三点弯曲条件下岩石的声发射特征. 文献[21-23]将声发射技术应用于压头静力侵入岩石试验，分析裂纹扩展与声发射能率、能量以及定位的关系. 关于滚刀破岩动态过程的声发射特征还未见报道.

本文在滚刀线性破岩试验中，采用声发射监测技术，结合滚刀破岩参数与试验现象，分析声发射信号特征与滚刀力、切削功、岩石损伤范围等的关系，总结滚刀与岩石间的作用规律.

1 试验设计

1.1 岩石试样

岩石试样为甘肃省玉门市的北山花岗岩(见图1)，长×宽×高分别为680 mm×680 mm×450 mm，基本物理力学指标见表1. 岩石表面光滑平整，能保证与传感器良好接触.

表1 北山花岗岩试样基本物理力学参数

1.2 试验装置

本试验采用北京工业大学自主研制的大型机械破岩试验平台[24](见图2). 该平台试样箱最大可容纳尺寸为1 000 mm×1 000 mm×600 mm的岩石试样，可对岩样施加围压，移动下方试样箱使岩石与滚刀产生相对运动，模拟TBM破岩过程. 通过调节刀具上下高度、试样箱左右位置和围压大小，可模拟不同贯入度、刀间距以及地应力等工况. 试验过程中还可采集滚刀三向力、位移和试验箱行走距离等参数，详细设计可参阅文献[24].

试验应用美国物理声学公司PCI- 8型声发射仪器(见图3)对试验过程进行监测. 利用该仪器的6个信号通道，选用R6α型传感器，其中心频率为60 kHz，频率响应范围为35～180 kHz，传感器布置见图4. 与声发射技术在金属材料中的应用不同，此处应用对象为岩石，且由于破岩试验的特性，产生的信号幅值较大，因此有必要对声发射仪器的各参数设置进行特别说明.

1) 前置放大系数：由于原始信号幅值较大，放大系数应设为最小，即20 dB.

2) 门槛值：试验发现门槛值设为50 dB可去除电磁噪声. 为去除二次声源的影响，还可将门槛再适当提高.

3) 滤波频段：对仪器最广滤波频段(1～400 kHz)下采集的信号进行分析后，发现信号频率分布在20～100 kHz，因此在仪器既定的几个滤波频段中选取20～100 kHz作为主要滤波段.

4) 采样频率：根据采样定理，采样频率大于2倍的信号最大频率即可. 本试验中信号的最大频率为100 kHz左右，因此可将采样频率设为1 MHz.

5) 采样时间：测试发现单个信号的持续时间均小于1 ms，因此采样时间设为1 ms即可.

6) 定时参数为峰值定义时间、撞击定义时间、撞击锁闭时间：由于岩石为复合材料，其定时参数分别取为50、200、300 μs.

1.3 试验方案

试验采用17英寸(432 mm)常截面盘形滚刀，滚刀间距为70 mm，x和y方向围压均为15 MPa，切割速度为20 mm/s. 贯入度取5组，分别为0.5、1.0、2.0、3.0、3.5 mm. 详细设计参数见表2.

表2 滚刀破岩实验设计参数

1.4 试验步骤

关于滚刀线性切割破岩试验过程，文献[7]已有详细描述，这里就不再赘述，以下主要介绍声发射相关部分的操作流程.

将岩石装入试验箱后，在指定位置安装传感器并用凡士林做耦合剂，敲击岩石表面以确定各通道是否正常工作. 围压加载完毕后，利用仪器自带的脉冲发射功能获取初步平均波速，并通过对若干已知点的定位结果进行修正. 试验开始后，根据设计的贯入度，由小到大分别进行线性切割试验，对每一切槽的声发射信号进行采集记录并确保与滚刀三向力数据同步. 试验结束后，对得到的声发射数据进行处理分析.

2 小波去噪处理

在滚刀破岩试验过程中，试验环境复杂，如试验箱的移动，滚刀对岩石的摩擦、冲击以及机械轰鸣等因素均可能对岩石声发射信号造成影响. 因此，有必要对得到的信号进行去噪处理.

小波变换是20世纪80年代发展起来的分析方法，该方法能对信号同时进行时域和频域分析，还可将信号进行多尺度分解得到各频段的波形，挑出能量占比较大的频段进行重构来达到去噪的目的. 小波变换由Fourier变换发展而来，Fourier变换以正弦函数为基函数，而小波变换则以一系列由基本小波函数自由伸缩平移得到的小波基作为基函数. 在L2(R)为平方可积的实数空间中(即能量有限的信号空间中)，若能找到函数ψ(t)L2(R)，且其Fourier变换Ψ(t)满足以下条件：

(1)

则称函数ψ(t)为一个基本小波或母小波. 对母小波进行伸缩和平移得到一系列子小波函数ψa,b(t)可表示为

(2)

式中：a为尺度因子；b为平移因子.

若有信号函数f(t)L2(R)，则其在小波基函数ψa,b(t)下的小波变换为

(3)

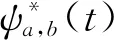
(4)

在处理岩石声发射信号时，大多应用Dubechies族小波基函数[25]. 本文利用Db5小波基对采集到的声发射信号进行4层分解，即将原始信号分解成低频和高频两部分，并在下一层分解中继续对上层低频部分进行分解，以此类推. 分解后得到各层重构信号并计算各层信号的能量比值，见图5，可以看出，信号能量主要集中在A4、D4、D3层，因此利用这3层的数据得到去噪后的信号. 如图6所示，该方法去除原声发射信号中的“毛刺”现象，有利于声发射定位中时差的准确获取.

3 声发射定位原理

声发射定位主要是利用源信号到达各传感器时间上的差值以及传感器的位置坐标，根据空间几何关系列出方程组并求解，从而得到声发射源的位置，其中假设波速在各个方向都相同且为常数. 如图7坐标系中的4个传感器Ti(i=1，2，3，4)和声发射源E，根据几何关系可得到方程组

(5)

式中：xi，yi，zi为第i个传感器的坐标值；x，y，z为声发射源坐标值；v为波速；ti为信号到达传感器时刻；t为源信号产生时刻.

求解式(5)便可确定声发射源E的位置坐标. 而求解算法主要有最小二乘法、Geiger法[26]和单纯形法[27]等方法，对比发现利用Geiger法和单纯形法得到的定位结果基本类似，因此本文主要利用Geiger法进行求解，并运用最小二乘法获得迭代初始值[28].

时差是声发射定位中的关键因素，微小的时差变化便可能引起较大的定位偏差. 信号在岩石中长距离传播会发生不同程度的衰减和畸变，导致各通道接收到的信号波形差异较大，因此常见的时差估计方法诸如阈值法、互相关法和峰值法等在此处并不适用. 本文利用一种基于AIC准则(赤池信息准则)的时差估计方法[29]对声发射信号到达时间点进行获取. 该方法通过公式

AIC(K)=Klg(var(x[1,K]))+
(N-K-1)lg(var(x[K+1,N]))

(6)

得到信号的AIC(K)曲线，见图8，曲线最低点便对应着信号的到达时间点. 式中：x为信号序列；K为时间点；N为采样长度；var为协方差.

4 试验结果及分析

试验时发现，图4里的8条切槽，只有在第5条切槽处切割时所有通道才正常工作，而在其他切槽切割时均会出现靠近切槽处的通道接收不到信号的问题. 同时也发现，在所有贯入度下，对于第1、2、3、6、7、8切槽，距离该切槽较远的2个通道均能较好工作. 以上现象主要是因为切割产生的信号幅值较大，如果在传播过程中又很少衰减，超出仪器的额定幅值范围将导致信号丢失. 因此，以下在分析声发射能率和能量时，以第6切槽的数据为例，统计通道5和6的信号结果，从而减少由于信号丢失带来的能量统计偏差. 而在声发射定位分析时，利用中间第5切槽的数据，以保证各通道能正常工作，方便定位.

4.1 声发射能率特征

声发射能率指单位时间里释放能量的多少，能率越大，声发射活动越剧烈. 图9给出不同贯入度下切割过程中能率与滚刀法向力的变化关系. 可以看出，能率与法向力具有相近的变化趋势，即法向力增大时能率增加，法向力减小时能率减少. 切割后的岩石表面往往是高低起伏变化的，当滚刀接触凸起部分时法向力增大，岩石内部裂纹萌生并迅速扩展，能率增加. 当裂纹贯通形成岩片或遇到凹陷部分时，法向力减小，能率也随之降低. 声发射能率很好地反映出切割时能量释放的过程.

4.2 声发射能量特征

声发射能量指材料发生变形或断裂时释放的应变能大小，滚刀破岩过程中的声发射能量主要包括岩石碎裂和裂纹扩展产生的能量. 统计同一切槽在不同贯入度下，所有切割层声发射能量平均值、平均法向力、平均滚动力和切削功，具体数据结果见表3.

表3 试验结果汇总

图10为声发射能量和平均法向力随贯入度的变化曲线. 由图可知，能量和平均法向力随贯入度的增加均呈增大的趋势. 这说明随着贯入度的增加，所需的推力增大，岩石破碎区变大，宏观裂纹贯通频繁，声发射活动增多且越发剧烈. 图中平均法向力曲线的斜率越来越小，即再增加贯入度只需要小幅地提高法向力，且滚刀下方岩石更为粉碎，裂纹发展尺寸加大，同时也产生更多声发射能量，侵入岩石将更容易.

图11为声发射能量和平均滚动力随贯入度的变化曲线. 可以看出，两者均随贯入度的增加而增大. 同时，由比能概念可知，通过切削岩石所做的功来表征破岩消耗的能量，而切削功又等于滚动力乘以切削距离[7]. 因此，绘制声发射能量与切削功的回归曲线，见图12，声发射能量与切削功基本呈线性关系，这表明声发射能量与切削功可以很好地对应，因此也可利用声发射能量来表征滚刀切削岩石所消耗的能量.

4.3 声发射损伤定位

声发射定位精度受诸多因素影响. 首先，在同时存在大量声发射源以及二次声源的干扰下并不能保证先后到达各通道的信号为同一源点信号. 其次，信号在传播过程中会发生不同程度的衰减和畸变，导致时差获取困难. 而且，计算模型要求声波速度在各方向上相同且为常数，但在试验中并不能得到保证. 对于本试验，情况更为复杂：岩石试样尺寸较大且可能存在裂隙，从而导致信号发生不同程度的衰减畸变，而且滚刀不断地对岩石造成损伤，损伤区和原岩区波速也并不一致. 目前并没有很好的解决办法. 由于声发射仪器幅值方面的限制，以下仅给出贯入度较小、信号幅值较低时的定位结果，其中定位点越大表示能量也越大.

图13为贯入度0.5 mm、第4层切割时的声发射三维定位. 可以看出，定位点主要集中在切槽正下方，显示为局部性破坏. 中间定位在高度上显示正常，但两端高度偏低，呈弯曲形态. 这是因为两端信号源点离各通道距离差异较大，信号波形在传播时发生不同程度的变形，导致时差获取有误造成的.

在贯入度较小时，切割1层后往往不能形成岩片，多次切割后才有岩片产生. 从图14可以看到，在贯入度1.0 mm的第1层切割中，岩石内部产生大量声发射活动但却并没有岩片形成，而是在下一层切割后才有岩片产生且该层声发射活动减弱. 图中的标记也表明，声发射大能量信号密集的区域正好对应着岩片形成的位置. 图15给出该切槽在岩片形成以前，贯入度0.5 mm的第4层、第7层和贯入度1.0 mm的第1层切割时某剖面的声发射定位. 由图可知，损伤深度在50 mm左右，且随着切割次数的增多，岩石损伤区域逐渐变大. 以上结果说明切割破岩是一个微裂纹积累、贯通直至形成岩片的过程.