舰炮伺服随动系统平稳性控制方法
2020-01-14曾庆旺张保山
曾庆旺,张保山
(1.中国人民解放军92941 部队,辽宁 葫芦岛 125001;2.江苏自动化研究所,江苏 连云港 222006)
0 引 言
舰炮随动系统控制策略通常采用PID 控制器,其输入信号是变化规律未知时间函数,要求被控对象按即定规律变化并与输入信号的误差保持在规定范围内。控制器参数调节的好坏直接影响控制系统的反应时间和稳定性[1-2],PID 控制器参数优化设计往往在单机检验时进行设定,在舰炮武器系统全系统联动时会根据系统控制精度再次进行PID 控制器参数调整,这依赖于经验公式或数据统计结果[3]。虽然舰炮随动反馈装置可以较好地满足系统的跟踪精度和快速性的要求,但是舰炮武器系统要适应不同作战需求,带炮样式中存在的非线性运动等不确定因素的存在,导致上述参数的设定并不能很好保证受控系统的快速性、准确性和平稳性。为了保证系统跟踪性能,除了提高分系统及设备自身的精度外,重要的是还需采用先进的控制策略,如为了适应非线性、慢时变、纯滞后、参数与结构的不确定性,解决传统PID 控制很难再得到理想的效果,采用参数自调整自适应PID 算法、模糊控制自适应PID 算法[4]、基于广义Hermite-Biehler 定理[5]等方法计算舰炮随动控制系统PID 控制器参数稳定域。上述伺服随动控制方法多基于经典控制理论,结合自适应处理、参数辨识的研究成果,侧重于舰炮本体进行控制,较少考虑对受控对象输入数据的约束限制。
(2) 稀疏性因子及迭代次数的选择.稀疏因子的作用是SNMF分解过程中控制稀疏矩阵的稀疏性,图7给出了不同稀疏因子所对应的目标函数误差(特征维数选为24,迭代次数为200).图7中可以看出:当系数因子等于0时,SNMF等价于NMF,会产生较大的目标函数误差;当目标因子不等于0时,虽然在理论上越大的稀疏因子就对应着更稀疏的稀疏矩阵,即得到最精炼的故障特征信息;目标函数的误差也随着稀疏因子的增大而增大,说明随着稀疏因子的增加,原始时频图像中所蕴含的故障特征信息损失也随之增加.
舰炮伺服控制系统通常采用的三环回路控制结构[6],即位置环、速度环、电流环。计算机作为位置环控制器核心,对整个伺服控制系统以及舰炮整体采取集中控制、离散处理。速度环和电流环分别集成在伺服驱动器内部,速度环和电流环采用PI 控制器。舰炮伺服系统的控制精度从选用更高精度的伺服驱动器以及执行机构和改进位置环控制器算法2 个方面进行提高,主要用于解决高速度和平稳度问题[7]。国内外学者考虑利用系统的动态特性和运动学信息,通过状态估计的方法,间接估计系统的速度。大部分文献则采用位置、速度控制环节,一是存在相应的相角滞后,影响系统的稳定裕度,甚至造成系统的不稳定;二是会降低系统带宽,造成系统响应速度变慢,跟踪能力下降。
舰炮随动系统为非线性控制系统,受舰艇摇摆影响,系统参数时变性强,具有大惯量、变负载、动平台的特征。某舰炮为了保证有快速的响应能力,在3 个环路又增加了加速度环。本文从舰炮伺服随动系统被告控制对象仿真模型出发,建立火控设备外部输入数据控制关系,分析产生随动不平稳的因素,给出了可行性改进措施,并根据作战样式进行了实船验证,对于研究舰炮PID 控制算法具有重要意义。
这个问题,青辰觉得在当前面对的所有问题中,似乎是最不打紧的一个。眼前有着更多关乎云浮命运的大事需要去解决。但师父有此发问,他只得老实作答。
1 舰炮随动控制系统建模
某舰炮质量重、惯性高,为了保证系统响应快的需求,在伺服系统中增加了加速度环路的建模控制,如图1 所示。
火控根据火炮架位反馈与当前火控预测量进行对比,当角误差较大时则采用大角度调转过程,否则使用火控设备的输出数据进行伺服控制。实际应用中尽管能保证快速调转,但对输入的速度量较敏感,出现了大角度调转过程中舰炮不稳定,低速跟踪过程中电机有异响等现象。
软阈值函数
穗长与产量的相关系数为0.35,直接通径系数为0.20,稍小于出籽率,通过活动积温和穗行数所起的作用为正向作用,而通过出籽率起的作用为轻微负向作用。穗行数与产量的相关系数为0.18,直接通径系数为0.13,通过活动积温、穗长和出籽率所起的作用为正向作用。
《中国经济周刊》对此刊发《二手房价格下跌,链家上海逆市上调中介费背后》一文,引发网友热议。已运行多年的“买方承担”潜规则,会否被中介巨头链家打破?
2 伺服随动控制火控角前馈平稳处理
2.1 跟踪过程处理方法
信号处理中采用频域分析方法,通过研究信号的频谱特征对信号处理,较常用的是离散傅里叶变换,但该方法不能表达时域信息,因此在某些方面应用还存在一定的局限性,后续发展为短时傅里叶变换可以表达时域信息,但在相空间中的分辨率是固定的,不能反应信号的瞬时特性,后来又发展了小波分析算法,充分发挥频域分析和时域分析的优点,提供了灵活的信号处理分析方法,并广泛应用于信号处理、图像处理、语音识别、雷达成像、医疗分析等领域。
设 f(t) 是 平方 可 积函 数,记 作 f(t )∈L2(R) , ψ(t)为母小波,若满足
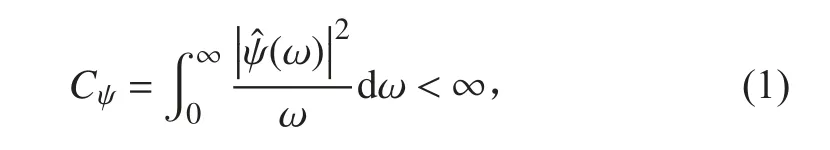
则
问题1:在△ABC≌△DEF中,AB=DE,BC=EF,AC=DF,∠A=∠D,∠B=∠E,∠C=∠F,则△ABC和△DEF全等吗?
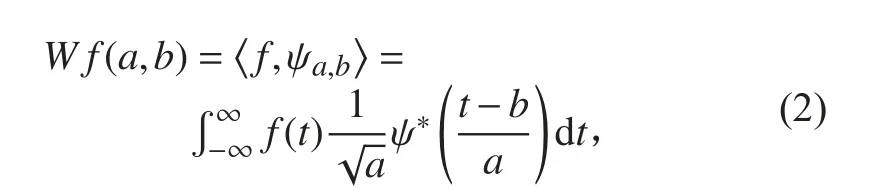
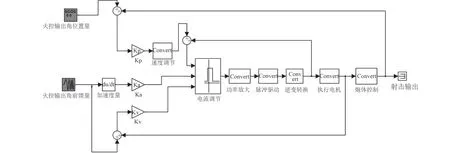
图 1 某舰炮伺服随动系统控制模型Fig.1 Control models of a naval gun servo system
式(2)称为 f(t)的 小波变换。其中 a 为尺度因子,b 为位移因子。若将上述因子在时间和位移域内的离散采样点上取值,称为对尺度因子 a 和位移因子 b进行离散化处理。常用的离散方法是对尺度因子按幂级数离散,选取j ∈Z , a0是大于1 的固定伸缩步长。当 j= 0 ,即 a==1时 , ψa,b(t)=ψ(t-b) ,此 时 b可以某一基本间隔 b0(b0>0) 作均匀采样, b0选择应满足香农采样定理。连续小波函数 ψa,b(t)按 照尺度因子 a和位移因子 b的离散化表示方法可以得到离散小波函数ψ j,k(t),即
(a) 原电机风道系统为坑道结构,按原系统结构改进,不利安装维修。且设计受坑道尺寸限制,考虑维修空间和增容加大的冷却器外形,现有的坑道空间限制了原系统结构改进。
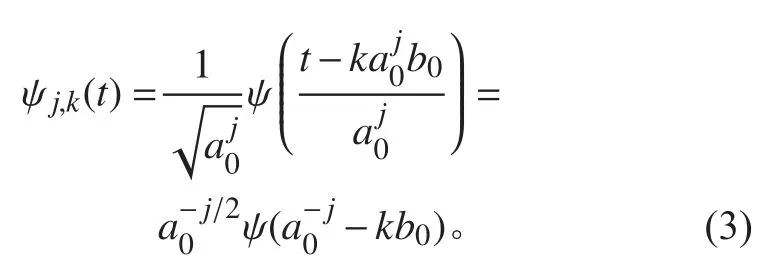
5c1H NMR(CDCl3) δ:7.80-7.78(m,1 H),7.63-7.61(m,2 H),7.27-7.25(m,5 H),3.75(s,3 H),2.40(s,3 H).
以加速段为例说明,如图5 所示。
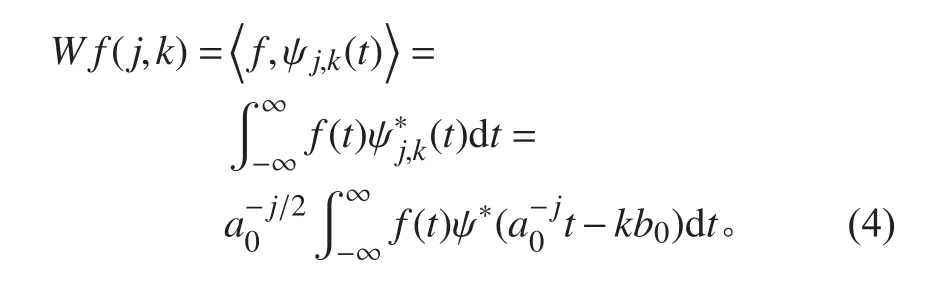
若 a 选取为2 的整数次幂,即 a0=2;位移因子归一化为 b0=1,得到二进制小波:
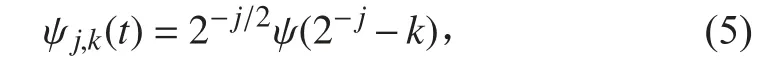
相应的二进制离散小波变换为
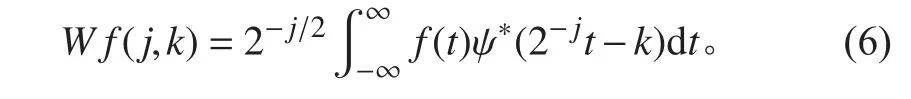
则满足如下原则:火炮架位 Rp经过加速、匀速、减速、过渡时间的行程与诸元预测位置 Rb相同;经过过渡阶段后,火炮架位控制的前馈值应与诸元的前馈vt相同。
传统成本管理过程中,成本信息量较大、部门沟通不及时、项目费用控制不到位等都是其主要的管理问题所在。在BIM项目成本信息管理中,工程管理人员借助基础平台层、数据资源层、业务支撑层、成本应用层和用户管理层五个层面的应用,有效的确保了成本管理的规范化:
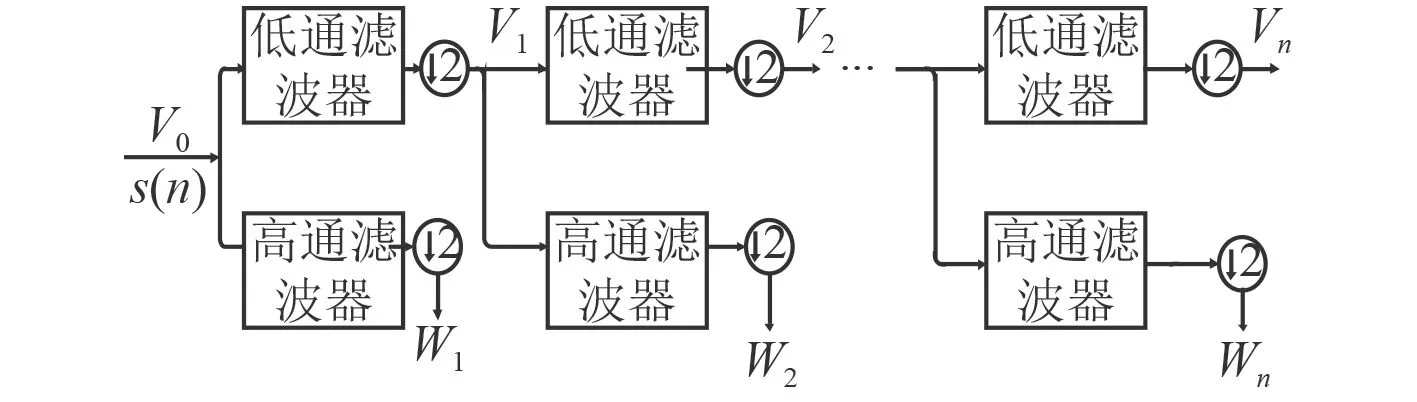
图 2 二进制离散小波变换二抽取空间分解图Fig.2 Wavelet packet decomposition tree
阈值选取有硬阈值和软阈值2 种处理方法[8]。软阈值处理是将信号的绝对值与阈值进行比较,不大于阈值的点变为零,大于阈值的点变为该点值减去阈值后向零考近。硬阈值则是将大于阈值的点保持不变,不大于阈值的点变为零。硬阈值较好保留信号边缘等局部特征,软阈值则是在硬阈值的基础上将边界外的不连续点收敛到零,可避免间断,重建信号比较光滑,工程上多采用软阈值方法。
产生上述现象的主要原因是舰炮随动系统对火控输出的角前馈量过于敏感,在角前馈的基础上又进行了一次微分控制,得到加速度量,同时增加利用加速度量对电流电机进行控制,当速度、加速度与实际运动不匹配或者火控解算角速度前馈含有噪声时,如舰炮阶跃或者跟踪速度不平稳。影响火控角速度解算精度的因素主要有:目标跟踪扰动误差、火控滤波预测误差、进行摇摆变换的舰船姿态数据误差、测量精度及数据传输误差、火控输出角前馈模型误差等,上述因素产生的误差在角位置上不明显,但是角前馈是根据角位置求导而来的,尽管火控在前馈输出时采用了平滑滤波处理,但在舰炮伺服控制又利用火控输出的角前馈量再次求导得到角加速度量,并在舰炮电流控制中增加这一控制量,同时根据角加速度量的大小进行电机控制以保证能够响应快速跟踪性能。
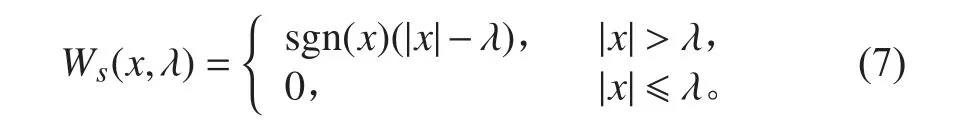
硬阈值函数
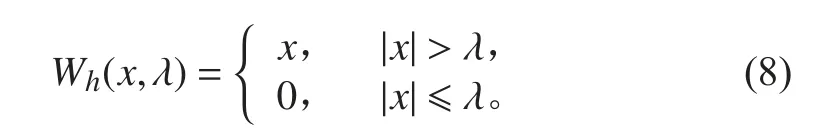
阈值的选取可以采用固定模型和Birge-Massart 策略确定阈值[9]。前者设定阈值,其中σ为噪声强度,n为信号长度。后者则给定一个指定的分解 层 数 N ,对 i(1 ≤i ≤N)层,保 留绝 对 值最 大 的ni=M(N+2-i)a个系数, M可选为第一层分解后系数的长度, a ∈ [1.5,3]。
为了克服硬阈值和软阈值缺陷,也提出了半软阈值方法[10]:
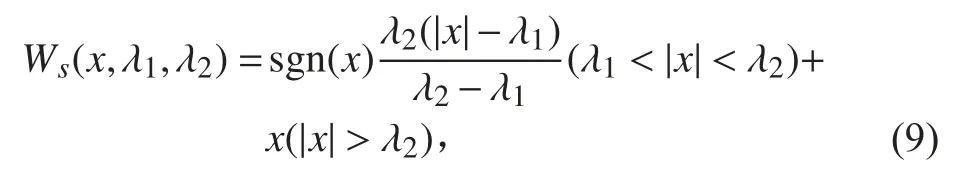
其中, 0 < λ1<λ2。
老年股骨颈骨折分型根据骨折解剖原理可分为头下、头颈以及基底等,按照Garden分型可分为单纯不完全骨折、完全骨折但无移位、完全骨折伴部分移位以及完全骨折和移位。

2.2 调转过程中带炮优化的基本原理
舰炮在正常跟踪过程之外,还存在调转、阶跃等大角度运动情况,这些往往考核舰炮的最大调转速度和反应时间,与跟踪时的信号不同,因此调转过程要从火炮的运动学方面进行建模。从当前舰炮架位加速向目标运动,可分为相遇问题和追赶问题。相遇时从当前架位加速向目标运动,并与目标反向行运动,共有加速段t1, 匀速段 t2, 减速段 t3, 过渡段 t4,如图3 所示。
火控设备输出的诸元反馈是非平稳的、非线性、非高斯信号,适用于上述信号处理的方法就是小波变换,可实现信噪分离,小波多分辨率分解能够将信号在不同的尺度上拓展,把信号分解为高频部分和低频部分,就可以使信号中有效成分和干扰噪声分离开。小波信号降噪的准则满足光滑性和相似性,光滑性是指大部分情况下,降噪后的信号至少和原信号具有同等的光滑性,相似性是指降噪后的信号和原信号的方差估计应满足极大极小均方误差最小准则。小波信号降噪的基本原理是选定一种小波,对信号进行N 层小波分解,对分解得到的各层系数特别是高频部分选取阈值处理,降噪处理后的数据通过小波重建恢复信号。
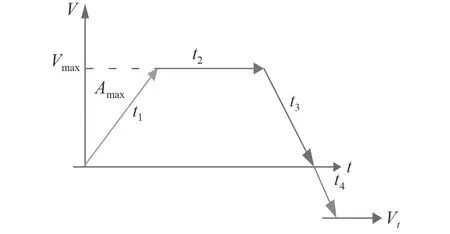
图 3 舰炮调转相遇示意图Fig.3 Pre drive gun intercept process
追赶时则需解决与目标同向运动时平稳过渡,共有加速段 t1, 匀速段 t2,减速段 t3,如图4 所示(为方便期间,此时假定过渡段 t4= 0)。
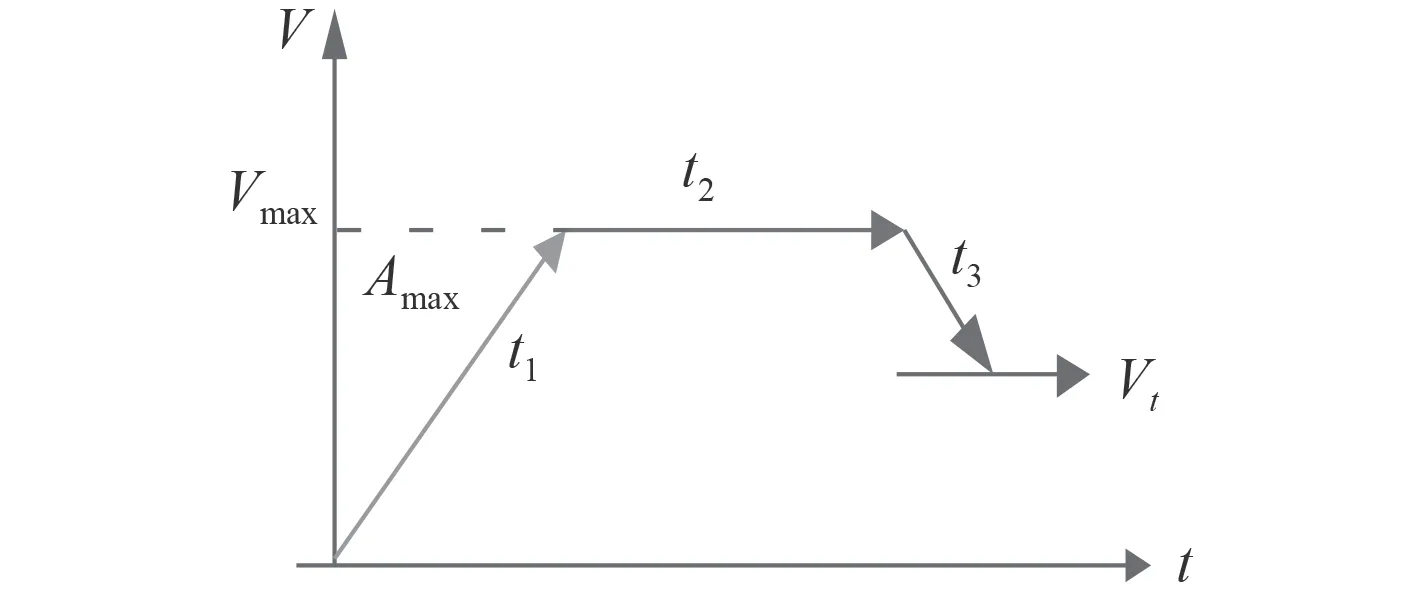
图 4 舰炮调转追赶示意图Fig.4 Pre drive gun pursuit process
设定火炮最大速度 Vmax,最大加速度 Amax,目标速度 vt,当前火炮架位 Rp,当前诸元位置 Rb。设 t1段的行 程为 s(t1) , t2段 的 行程 为 Vmaxt2, t3段 的 行程为 s(t3),过渡段的行程为 s(t4)。
对于二进制离散小波变换,可以从频率空间的部分导出。如果将原始信号 s(n) 定义为空间 V0,经过第一级分解后 V0被划分为低频 V1子 空间和高频 W1子空间,且 V0=V1⊕W1, 将 V1继续分解下去,可以得到一系列空间分解 V1=V2⊕W2,···,这种二抽取可将输入序列每隔一个输出一次,组成长度缩短一半的新序列。
推导出相应的离散小波变换
改进的软阈值方法:
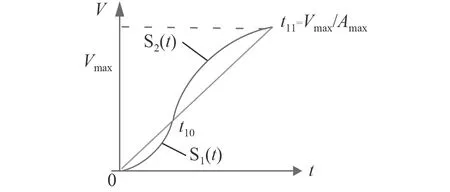
图 5 舰炮调转加速过程示意图Fig.5 Pre drive gun acceleration process
按如下原理进行处理时,需满足2 个条件,初始速度为0,加速度结束达到最大速度 Vmax,同时在 t1运行的时间内行程与匀加速行程相同。设第1 段速度运动函数为 s1(t), 第2 段速度运动函数为 s2(t)。则须满足如下条件:
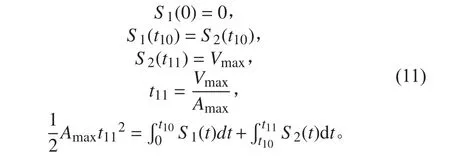
3 仿真计算结果分析
设原始信号为 xi( 0 ≤i ≤N),采用小波变换降噪重构后的信号为,在信号噪声处理时,定义范数 L1, L2, L∞。
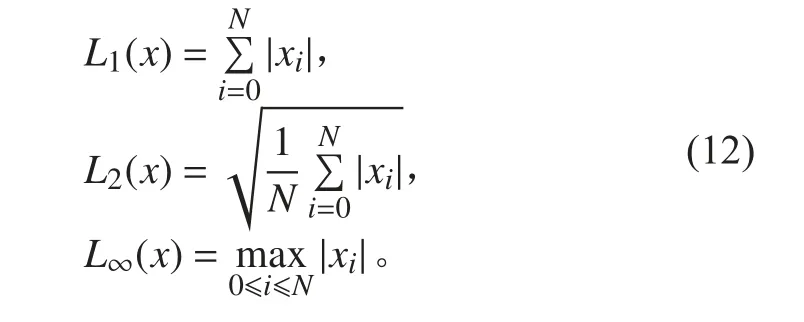
信噪比定义
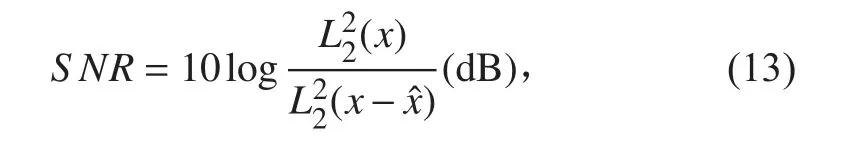
定义相应的能量比

其中:p 表示1,2, ∞。
卵巢老化状态下生物学特征的表现主要依赖于生化检测,而超声为主要的影像学检测手段,可有效检出AFC及卵巢容积[17]。本研究显示试验组与对照组的AFC分别为(6.10±0.42)个和(13.39±3.28)个,试验组明显低于对照组(P<0.05)。并且AFC检查无创、价廉,是评价卵巢储备的最佳指标之一,也是生殖医学专业医生较易掌握的一门技术。从机制上推断卵巢子宫内膜异位囊肿患者卵泡内存在某些物质,从而阻碍优势卵泡的选择和进一步发育。
信噪比和能量比能够反映噪声前后的改善因子,因此仿真计算中可作为衡量小波变换质量的评估要素。 L∞范数仅考虑变换前后最大值的对比,关注信号最大幅度的情形,而未考虑信号的全局特征,在应用中还存在一定局限性,通常采用 L1, L2范数进行评估。图6 给出了基于 L2范数的不同层数能量比和信噪比图例,表1 列出了不同小波变换在3 种范数下能量比和信噪比的计算结果。
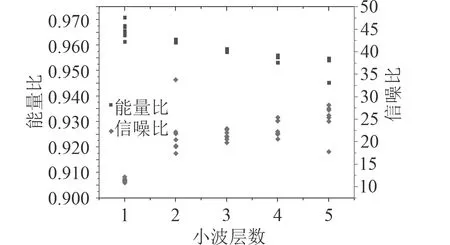
图 6 不同小波变换层数能量比及信噪比图Fig.6 Energy ratio and SNR of different wavelet levels
从图6 和表1 可以看出,经过2 层小波降噪重构后信号信噪比SNR 可达20 dB, L2范数能量比可达96%,随着层数增加,信噪比及能量比提升有限,另外随着层数的增加,也需要更多的存储空间和计算时间,工程上受计算速度和空间的限制,采用了2 层小波降噪和重构过程,即可满足使用要求,对火控输出的前馈量进行了2 层小波降噪处理的结果如图7所示。
采用带炮优化的前馈处理过程见图8 和图9,火炮协调过程前馈平稳。
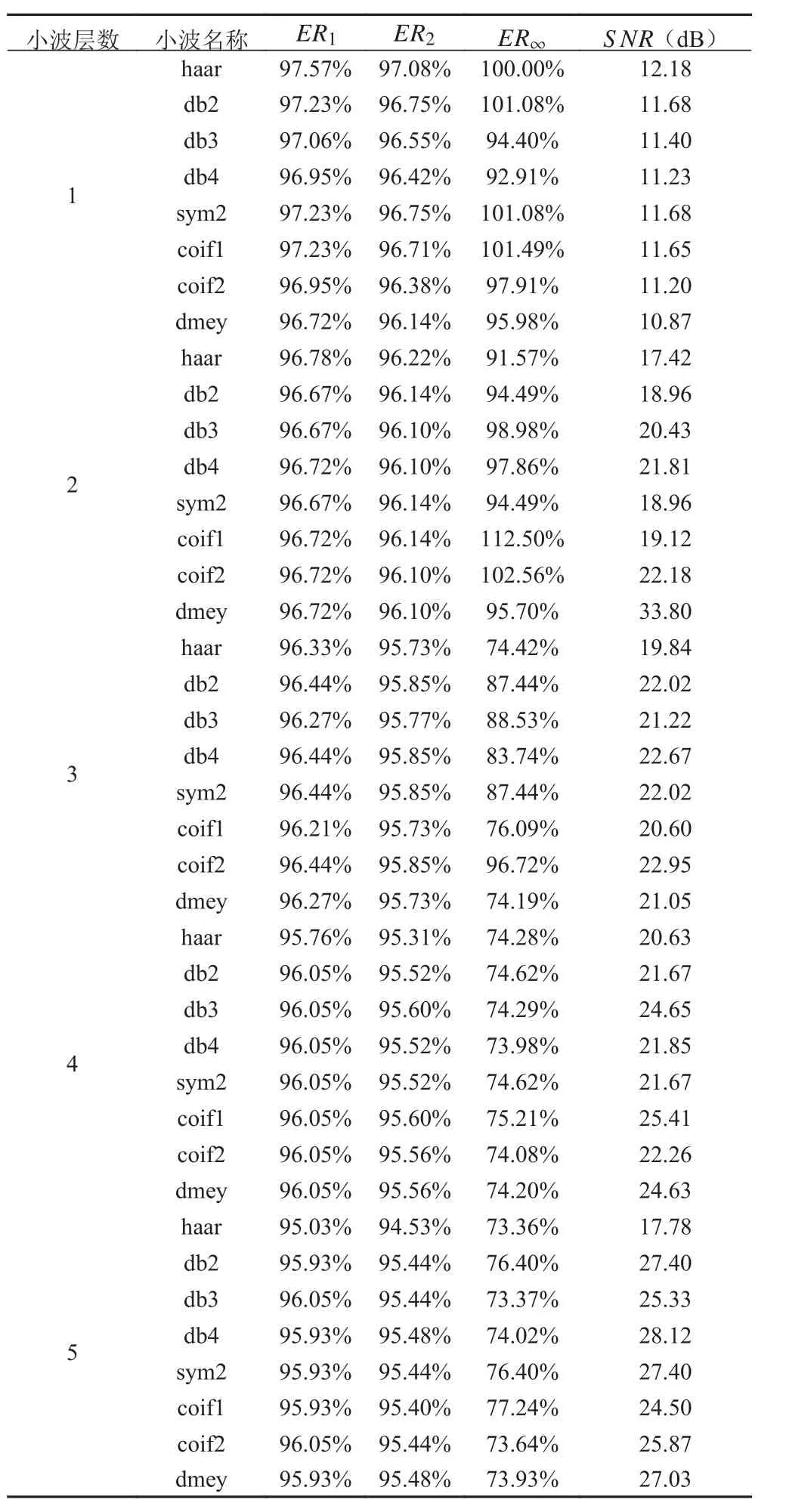
表 1 不同小波降噪重构后信号能量比及信噪比Tab.1 Energy ratio and SNR of different wavelet denoising reconstruction
4 结 语
舰炮伺服随动系统采用PID 控制机理,引入加速度量控制虽能满足舰炮武器系统快速响应的需求,但也带来了火控输出前馈敏感性现象。本文从小波变换信号降噪重构和调转过程运动建模,对火控输出前馈进行平滑处理,解决了高灵敏度舰炮伺服运动过程中的快速响应和平稳性问题。该方法在装备中得到了应用,在满足系统跟踪精度技术指标的前提下,实现了对大惯量、变负载、动平台舰炮本体的平稳性控制,可为工程应用提供参考。
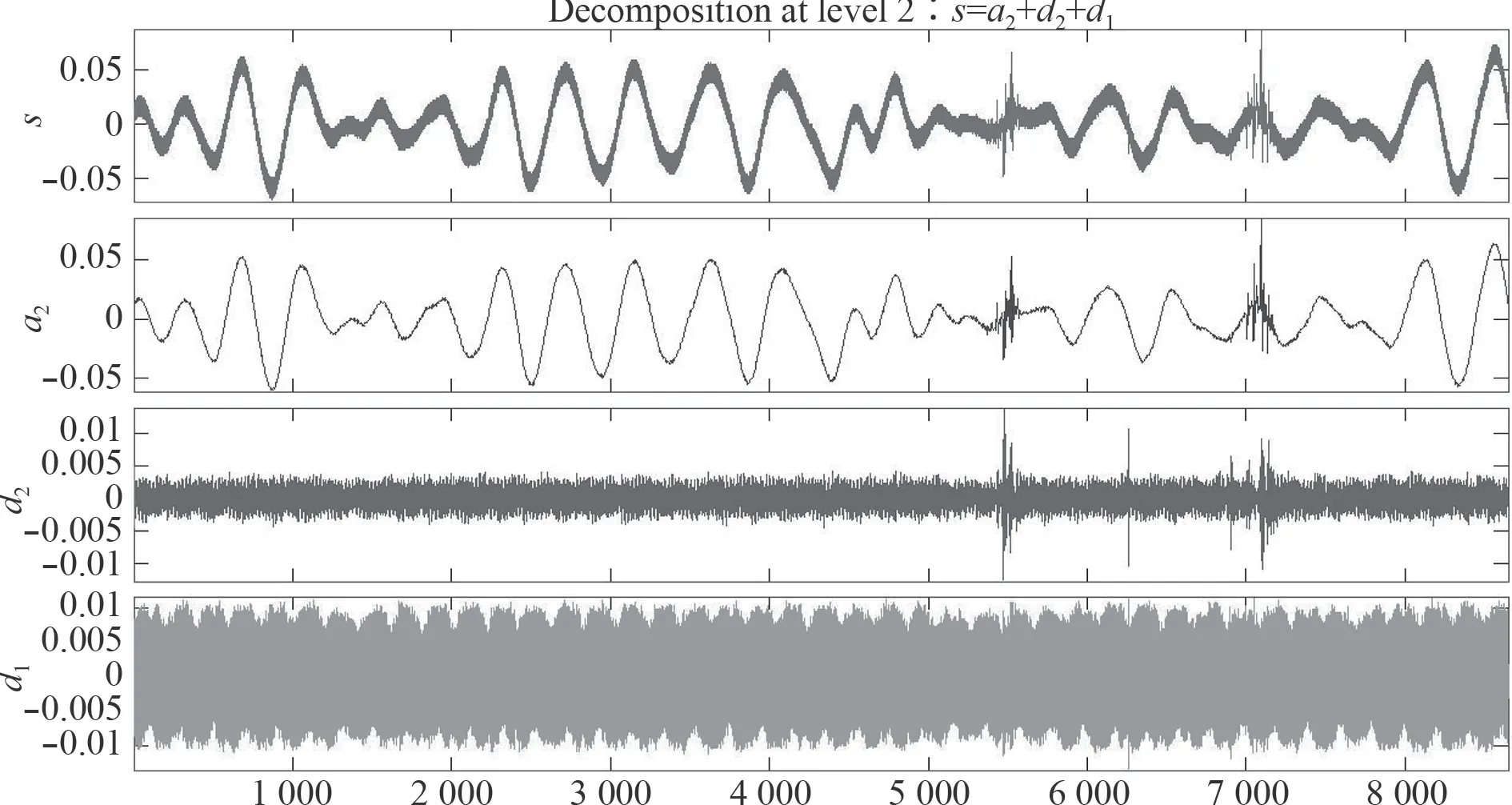
图 7 跟踪速度前馈的小波2 层降噪过程Fig.7 Gun tracking velocity wavelet decomposition at level 2
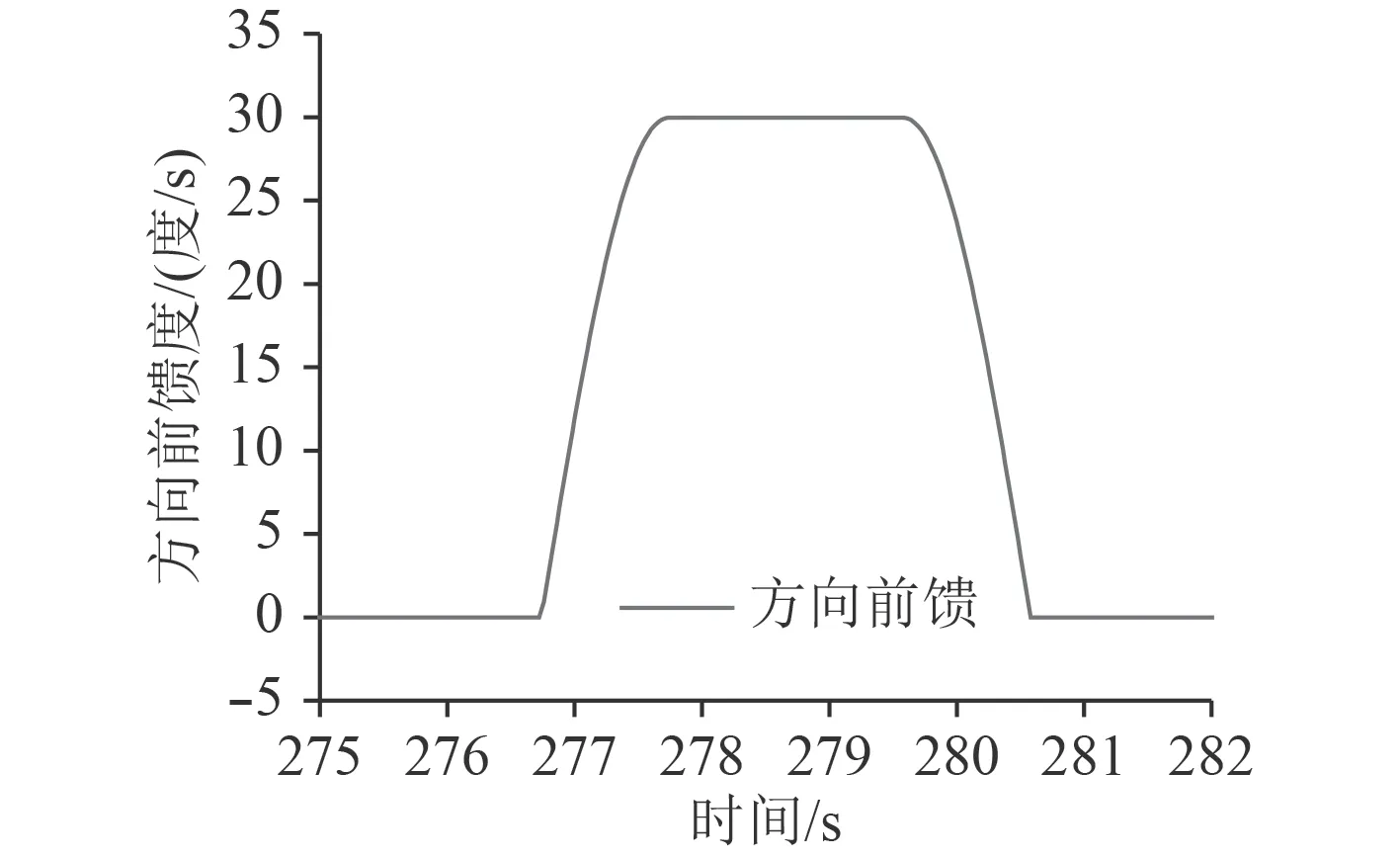
图 8 预先带炮方向前馈图Fig.8 Pre drive gun bearing velocity
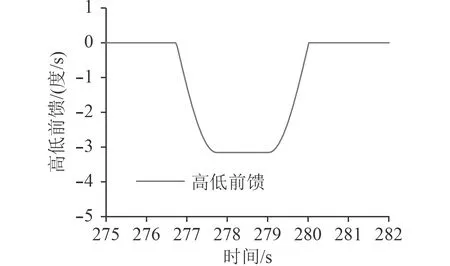
图 9 预先带炮高低前馈图Fig.9 Pre drive gun elevation velocity
