船舱用升降装置的振动试验与分析

高治华，赵建波，戴宗妙，熊珍凯

(中国船舶重工集团公司 第七一三研究所，河南 郑州 450015)

0 引 言

货物在船舱存储时，需要进行水平搬运和竖直搬运，升降装置是该环节的重要设备之一。某船用货物升降装置具有提升载荷大、运行速度高的特点，使用过程中存在振动和噪声辐射等问题，对船舱内工作环境和产品本身的性能产生影响。当结构发生共振时，设备的动应力和噪声会显著增加，影响设备使用寿命。为保证设备长期可靠工作，有必要对该升降装置工作时的振动特性进行测试和分析。

振动烈度是能够反映设备振动状态的实用有效的特征量，目前在大、中型机电设备的振动检测和状态评估研究中已长期应用[1-4]，其理论基础比较成熟，利用该理论开展升降装置状态评估是完全可行的。本文在工作状态下对升降装置的振动加速度进行测试和分析，并使用频域算法对振动烈度进行分析，旨在掌握该升降装置的振动特性和振动烈度等级。在Ansys Workbench 平台研究该升降装置的振动模态，对比了振动测试和模态分析结果，用于指导设备振动特性改进设计。

1 计算和分析方法

1.1 振动烈度计算方法

振动烈度是表示机电设备振动强烈程度的量，通常采用振动速度有效值的合成值表征振动烈度。试验中，测得升降装置基座各测点在各方向的振动加速度离散信号，通过时域积分的方法得到各测点在各方向的振动速度信号，然后通过频域计算方法计算各测点在各方向的振动烈度，最后合成得到各测点的振动烈度。振动烈度的频域计算方法[5-6]利用离散傅里叶变换（DFT）理论，可得频域上信号 X( k)的表达式：

式中： x(n) 表示实测 N点振动信号。进而求得信号的单边幅值谱 Ak和谐波频率 fk为：

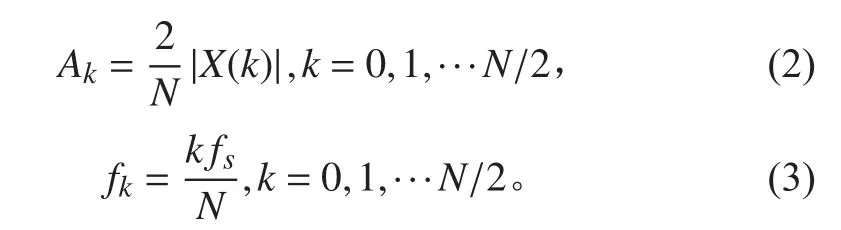
计算频率范围为 fa～fb上 的振动烈度。记 ka为不小于 N fa/fs的最小整数， kb为 不大于 N fb/fs的最大整数，即 ka是最接近且不小于计算频率下限 fa的谱线序号，kb是 最接近且不小于计算频率上限 fb的谱线序号。当x(n) 为振动速度信号，则在频率范围 fa～fb上的振动烈度为：

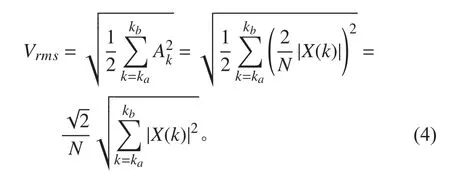
式 中： fs为 信 号 采样频率； ka为 不 小 于 N fa/fs的 最 小 整数； kb为 不大于 N fb/fs的最 大整数。

振动烈度的频域计算方法相对于时域计算方法适应性强，能够提取振动位移、速度和加速度的烈度特征，可以根据需要选取一定的频域范围计算烈度值。

根据国家标准GB/T16301《船舶机舱辅机振动烈度的测量和评价》，当测点的振动按照3 个相互垂直方向测试时，对各测点的振动烈度按照下式合成：

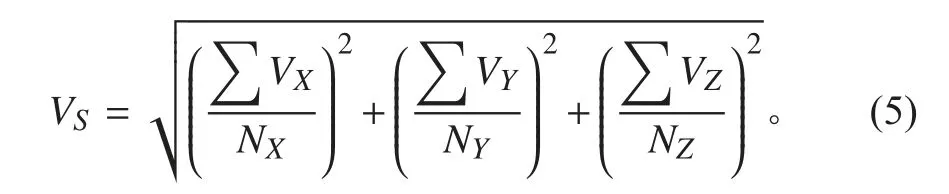
式中： VS为振动烈度； VX， VY， VZ为3 个相互垂直方向上的振动速度有效值； NX， NY， NZ为3 个相互垂直方向上的测点数。

1.2 模态分析方法

设备的模态由结构本身特性和材料的特性所决定，与外部载荷大小无关。模态分析利用系统固有频率的正交性，以系统的各阶模态向量所组成的模态矩阵作为变换矩阵，对选取的物理坐标进行线性变换，使得振动系统以物理坐标和物理参数所描述的、相互耦合的运动方程组能够变为一组独立的模态方程。模态分析主要有试验模态分析和有限元模态分析2 种方法。试验模态分析是将试验与理论分析结合起来辨识系统的固有频率和振型；有限元模态分析主要运用有限元法对振动结构进行离散，求取振动结构固有频率及其相应振型。由于升降装置体积较大、结构较复杂，本文采用有限元模态分析方法进行研究。升降装置主体为钢结构体，可视作小阻尼多自由度系统[7-8]，其振动微分方程为：

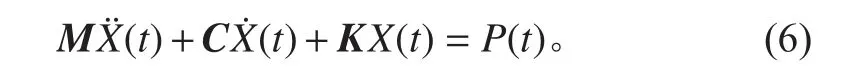
式中： M， C ， K分别为质量矩阵，阻尼矩阵和刚度矩阵；， X(t)分别为加速度向量，速度向量和位移向量； P(t)为载荷向量。

式（6）为有阻尼的多自由度系统的强迫振动微分方程，而固有频率分析一般可看作无阻尼自由振动，则式（6）变为：

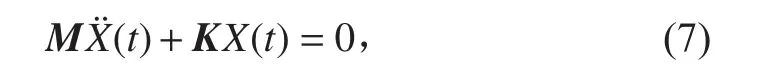
有非零解的充分必要条件是系数矩阵行列式等于0，即特征方程为：

求解特征方程可得到升降装置的固有频率。目前有较多的有限元模态分析的软件，本文选用Ansys Workbench 软件进行升降装置的模态分析研究。

2 试验情况

根据升降装置的电机工作转速为1 700 r/min，确定试验系统组成如图1 所示。其中使用1 台西门子SCM05 型动态信号分析仪，12 个美国PCB 333B32 型加速度计，测量范围为0.5～3 000 Hz，灵敏度为100 mV/g，12 个333B32 型加速度计合成4 组三向加速度计，能够满足测量要求。

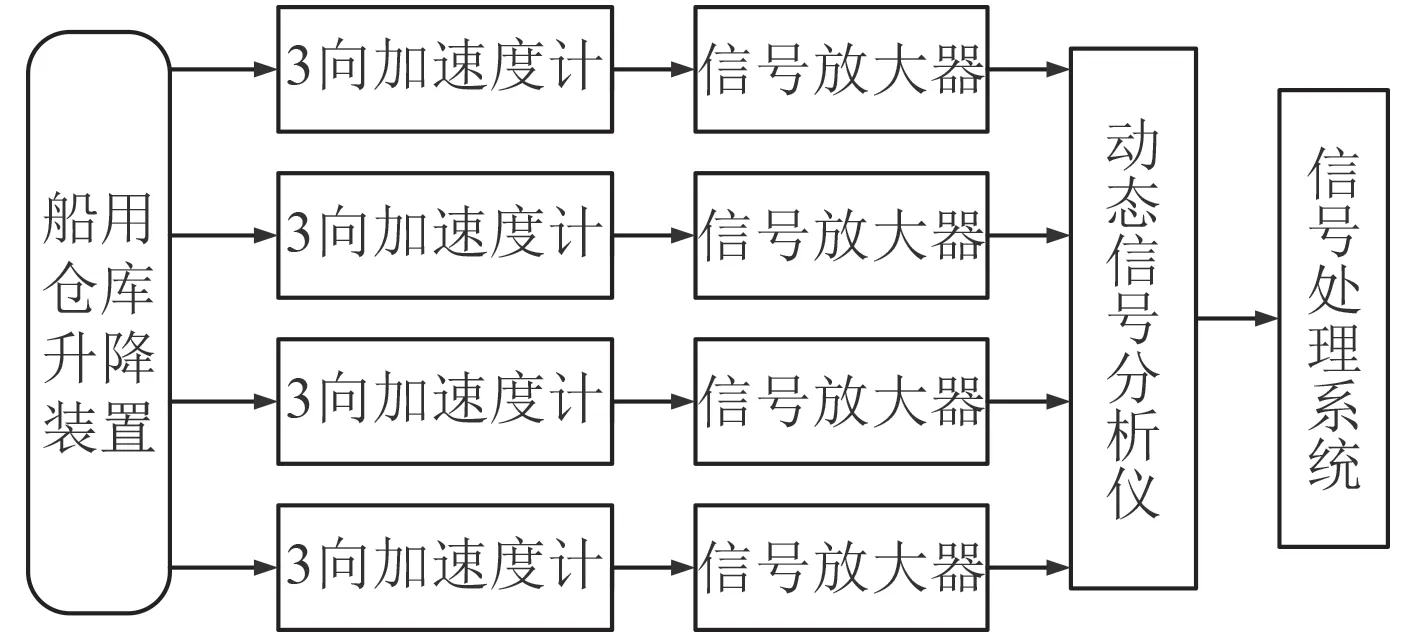
图 1 试验系统组成Fig.1 Composition of test system

在电机额定工作转速1 700 r/min，提升载荷2 t 的条件下进行测试，升降装置的顶部和底部基座分别固定在船体结构上，在升降装置的顶部和底部基座上各布置2 个测点，对每个测点采集X，Y，Z 三向的振动加速度，采样频率为20 480 Hz，其中1 个加速度计测量方向垂直基座安装面，升降装置的顶部基座具体测点位置和方向如图2 所示。

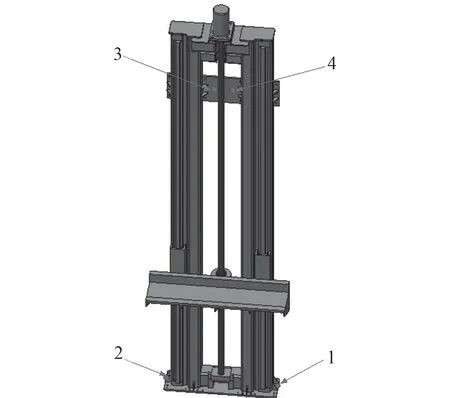
图 2 试验测点布置Fig.2 Layout of measuring points

3 试验分析

3.1 振动特性分析

试验中，升降装置稳定运行过程中利用加速度计对4 个测点的振动加速度信号进行采集，每个测点有X，Y，Z 三向加速度信息，选取稳定运行阶段的5 s的信息进行分析，下面列出2 号测点和4 号测点分析结果，2 号测点和4 号测点加速度时域图如图3 所示。通过信号处理和傅里叶变换得到加速度1～1 000 Hz 频谱图如图4 所示。通过加速度信息时域积分的方法得到测点各方向的振动速度信号[9-11]，速度时域图如图5所示。试验中，振动测量误差主要来源于加速度计线性误差、频率响应误差、动态信号分析仪误差和粘贴时传感器轴向与测点轴线偏差所引起误差。振动加速度计线性误差为1%；振动加速度计频率响应误差为5%；动态信号分析仪误差为0.5%；粘贴引入误差为1%；按均匀分布计算，则振动烈度试验系统的扩展不确定度为：U=1.8×10-2（k=2），满足GB/t 16301 的测量要求。

统计2 号、4 号测点在0.5～1 000 Hz 范围内振动加速度比较大时的频率，如表1 所示。电机额定工作转速1 700 r/min，对应转动频率为28.33 Hz，从表1和图4 可以看出，振动加速度比较大时均出现在电机转动频率的倍频处，且大部分出现在电机转动频率的10 倍频（283.3 Hz）以上，说明电机转动频率低倍频工作时升降装置振动力较小。

按照式（1）～式（5），根据各测点的振动速度计算各测点的振动烈度，结果如表2 所示。

可以看出1 号、2 号测点在Y 向振动烈度最大，3 号、4 号测点在Z 向振动烈度最大，根据GB/T 16301对升降装置整体进行评价，升降装置整体在Y 向振动烈度最大，振动烈度合成值为6.74E-4 m/s，符合第一类辅机A 级（优良工作状态）的要求，说明升降装置工作时振动强度小，对周围环境的设备影响较小。

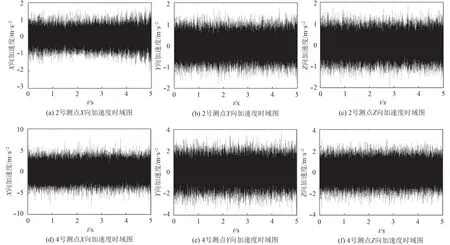
图 3 测点加速度时域图Fig.3 Time domain map of measuring points acceleration

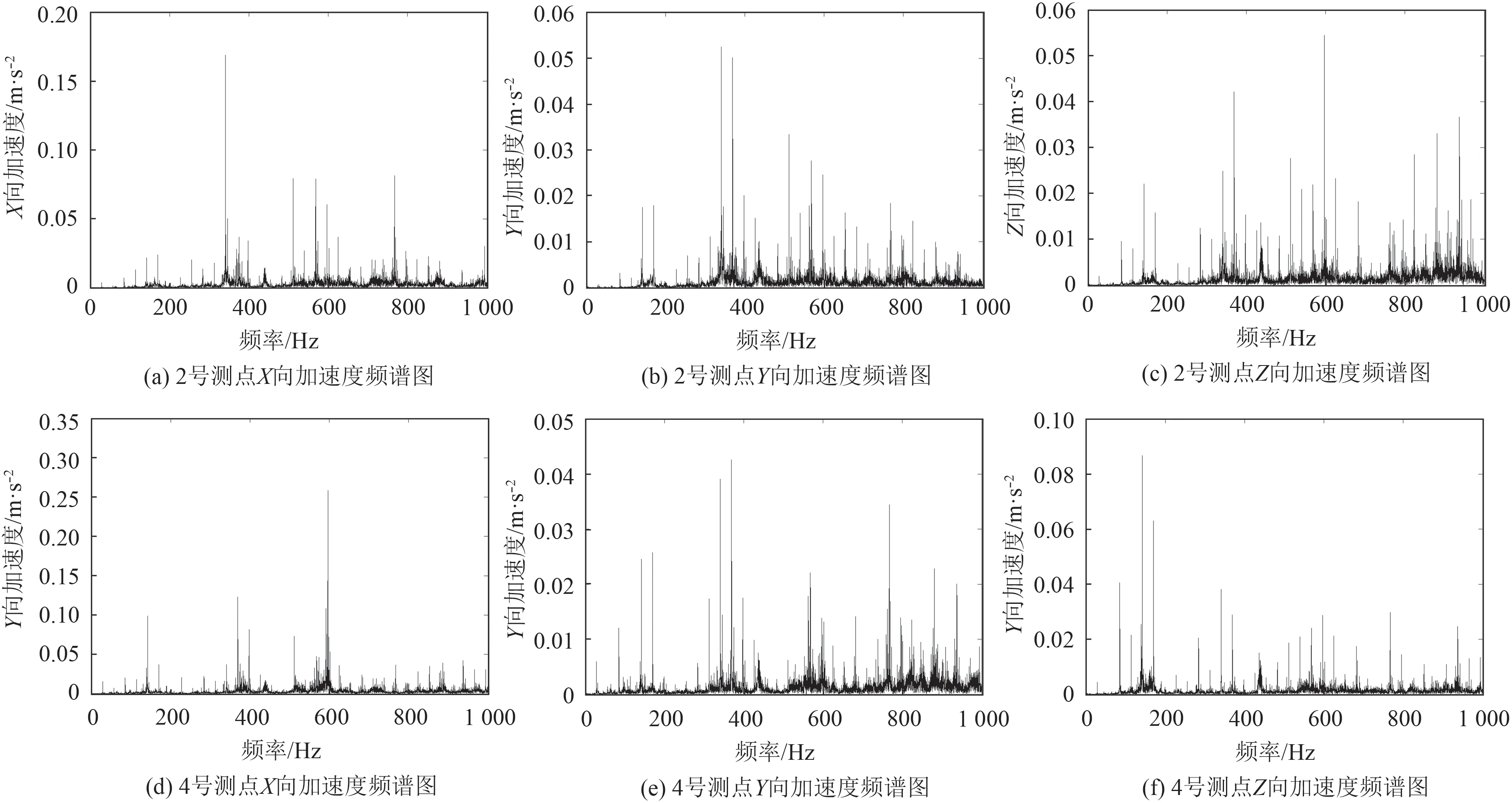
图 4 测点加速度频谱图Fig.4 Spectrogram of measuring points acceleration

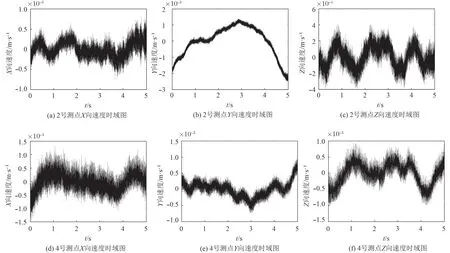
图 5 测点速度时域图Fig.5 Time domain map of measuring point velocity

3.2 模态分析

建立正确的模型是有限元模态分析的基础。本文使用Pro/E 三维软件对升降装置进行建模。Pro/E 是目前先进的计算机辅助设计、分析与制造软件之一，具有强大的实体造型、虚拟装配和产生工程图等设计功能，同时Pro/E 可以与Ansys Workbench 联合仿真，便于模型处理和提高仿真效率。为提高仿真单元质量、减少仿真分析耗时，考虑到升降装置传动丝杠为受拉状态，不影响整体结构的模态振型，对其和升降装置模型中的孔、倒角等结构适当的简化。在Pro/E 中完成三维模型建立后导入Ansys Workbench 中，选用modal 模块进行分析。首先进行网格划分，在门架主体采用大尺寸网格划分，其余的零部件采用确定尺寸进行网格划分，如图6 所示。

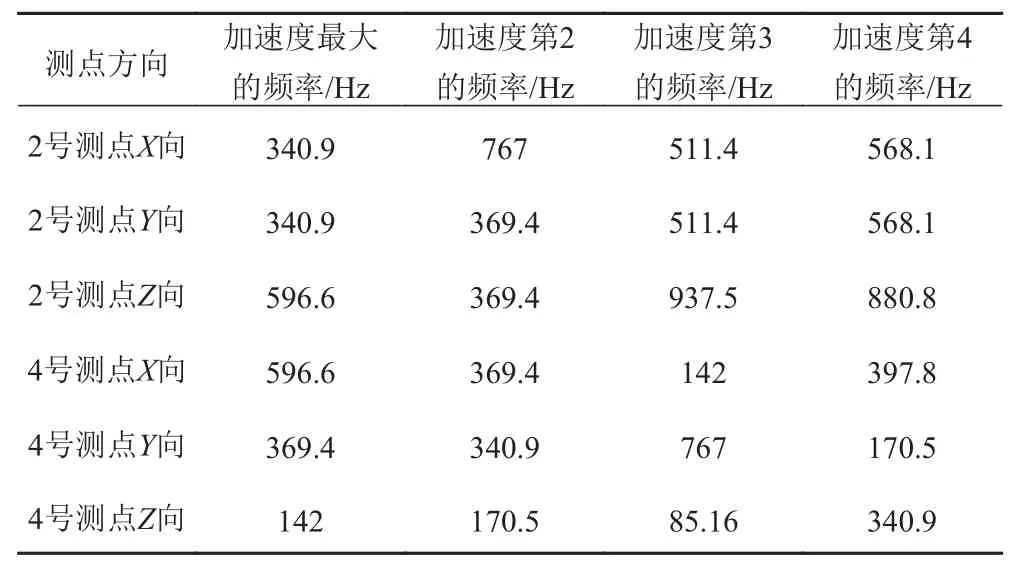
表 1 测点在0.5～1000 Hz 范围内振动加速度统计Tab.1 Vibration acceleration statistics of measuring points in the range of 0.5～1000 Hz

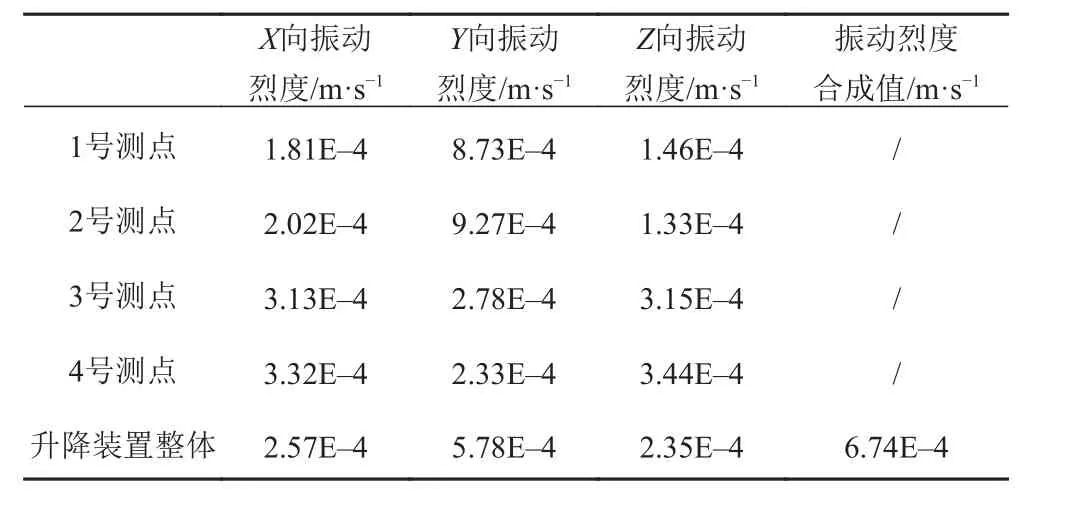
表 2 测点振动烈度统计Tab.2 Vibration intensity statistics of measuring points

图 6 升降装置模型网格划分图Fig.6 Meshing diagram of lifting device model

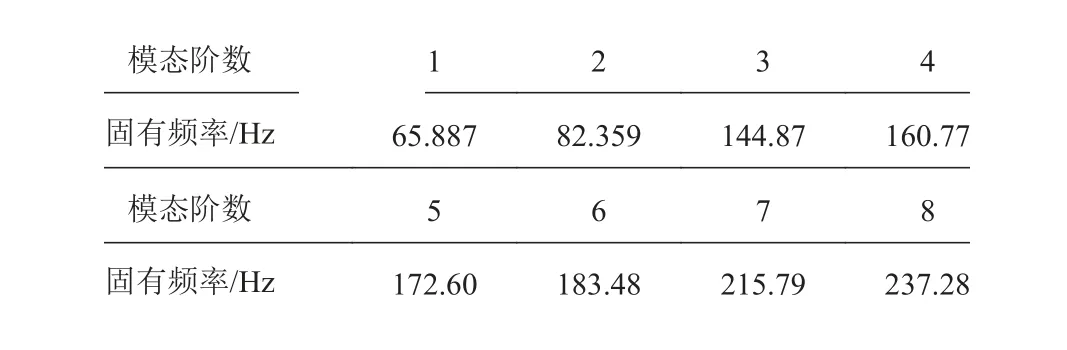
表 3 升降装置前8 阶固有频率Tab.3 First 8-order natural frequencies of lifting device

按照实际使用工况对升降装置的顶部基座和底部基座采用固定约束。以升降装置中心位置为基准建立了有限元网格模型，该模型中总节点数为2 288 131个，总单元格数为1 154 788 个。通过对升降装置模型进行有限元模态分析，可得到前8 阶模态振型图和固有频率，如图7 和表3 所示。

图7 中，1 阶模态图表示门架中部沿X 轴方向弯曲变形，工作中为减小门架的变形，需采用刚性较强的结构，2 阶模态图表示门架中部整体沿Z 轴方向的单方向弯曲变形，3 阶模态图表示门架顶部和中部沿X 轴方向的弯曲变形，4 阶模态图表示门架中部在ZY 平面的两方向弯曲变形，5 阶模态和6 阶模态图表示升降台前沿Y 方向的弯曲变形，7 阶模态图表示升降台绕X 轴的扭曲变形和门架沿X 轴方向的弯曲变形，8 阶模态图表示门架中下部在ZY 平面的两方向弯曲变形。通过对整个升降装置进行模态分析，前8 阶固有频率集中在50～300 Hz 的范围内。当升降装置空载或满载工作时，避免激振频率与固有频率相同或相近，防止升降装置零部件发生较大振动而失效。

对比表2 和表3，可以看出在升降装置电机转动频率的10 倍频（283.3 Hz）内，4 号测点振动加速度在转动频率的5 倍频（141.7 Hz）、6 倍频（170 Hz）和3 倍频（85 Hz）附近出现较大值，分别对应升降装置的3 阶、5 阶和2 阶模态固有频率，说明在固有频率与转动频率各倍频接近时，易产生较大的振动力，在设计时应尽量将两者分开。

4 结 语

根据振动烈度测试结果对升降装置振动强度进行评价，升降装置在Y 向振动烈度最大，整体振动烈度合成值为6.74E-4 m/s，符合第一类辅机A 级（优良工作状态）的要求，说明升降装置工作时振动强度小，对周围环境的设备影响较小。通过对比振动加速度测试结果和升降装置固有频率，说明在固有频率与转动频率各倍频接近时，更易产生较大的振动力，在设计时应尽量将两者分开，对于设计过程中降低设备振动提供指导和参考。