圆阵及线圆组合阵声源定位方法仿真
2020-01-14吕孟婷张啸天
吕孟婷,张啸天
(大连测控技术研究所,辽宁 大连 116013)
0 引 言
舰船辐射噪声是评价舰船隐蔽性的重要指标之一,如何对潜艇机械噪声源进行精确地定位,对其传递途径进行判断,准确查找潜艇机械噪声的来源,是潜艇机械噪声控制和减震降噪工作的重要环节[1]。
通过大量理论研究与实验测试发现,影响声源定位精度的因素诸多,其中阵列几何结构是影响阵列声源定位精度的一个重要因素[2]。阵列结构问题已在阵列细化技术研究领域中被提出,其研究多侧重在结构优化方面,近几年国内出现很多关于阵列结构形式的声源定位性能研究报道,包括线性阵[3]、平面阵列[4]和立体阵列[5-6]。分析可知任何一种阵列结构均由阵元按照不同方式构成,不同的阵列结构在声源的定位性能上各有差异,因此阵列结构对噪声源定位技术的基础性作用不容忽视。
本文着眼于研究不同阵列结构对声源定位性能的影响,首先建立n 元基阵的数学模型,给出线阵,线圆组合阵模型中各阵元几何关系方程组,在此基础上,分别推导了线阵、线圆组合阵的定位算法。最后进行仿真实验,分析不同阵列结构和算法在不同条件下的最优组合。
1 阵列的数学模型
首先,假设存在M 个窄带信号,阵列由N 个阵元组成,阵列中每个阵元的最终输出都可以表示为M 个再带信号与加性噪声的和。因此,将N 个阵元在特定时刻接受的信号排列成一个列矢量,可得窄带远场信号的DOA 数学模型:
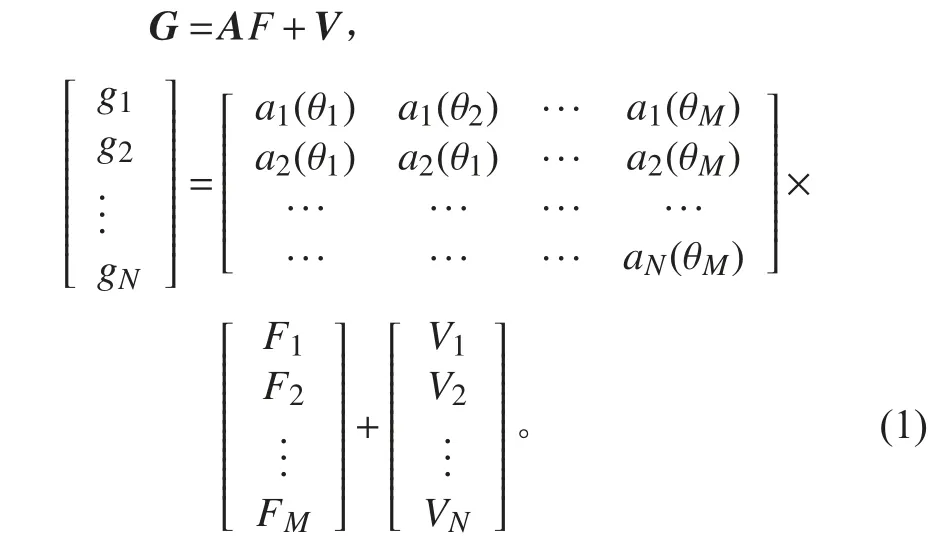
式中:G 为阵列的快拍数据矢量;V 为噪声数据矢量;F 为空间信号矢量;A 为空间阵列的流型矩阵。
1.1 圆阵的数学模型
利用平面阵列可以获取目标声源的方位角和俯仰角,典型的平面阵列包括圆阵和矩形阵列。圆阵的阵元结构如图1 所示,圆阵的半径为 R0,阵元数为N(q=0 1···N-1)。阵列在X-Y 平面上,参考阵元位于X 轴上(q=0)。阵元位置与角度的关系: φ0=2π/N。
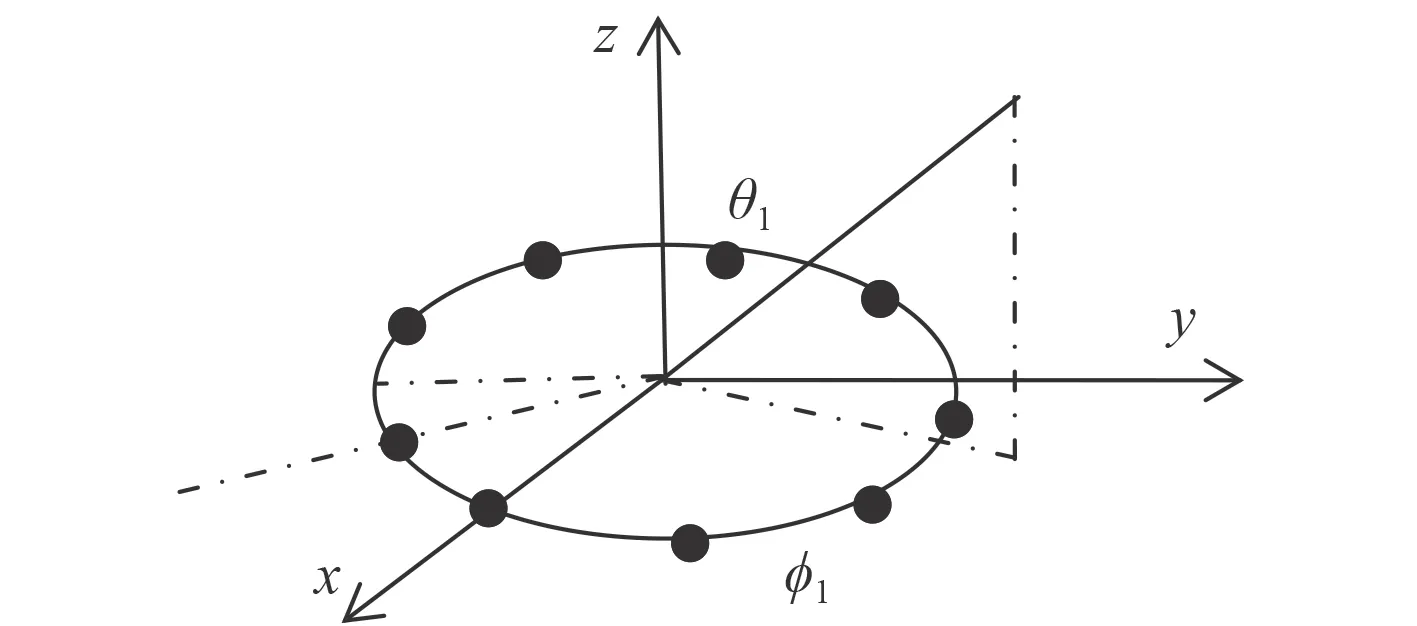
图 1 圆阵Fig.1 Circular array
假设平面波的振幅为 A1,频率为 f1,入射角为( φ1,θ1)。则第q 个阵元的信号输出可以写成:
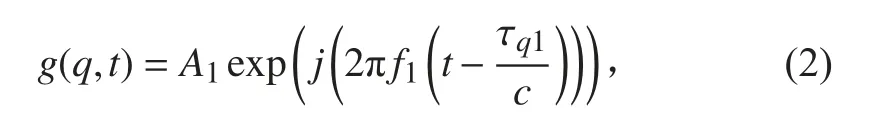
其中, τq1为阵元q 相对于参考阵元的空间延迟
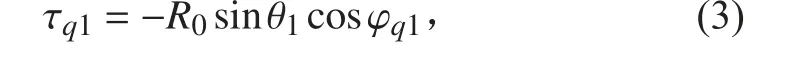
在这种情况下,因为阵元的方位角间隔相等,所以 φq1可以写成:

因此
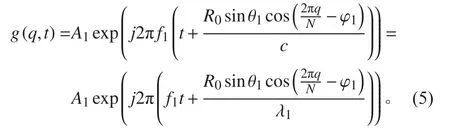
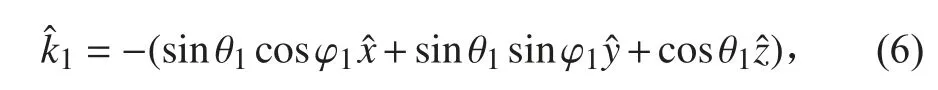
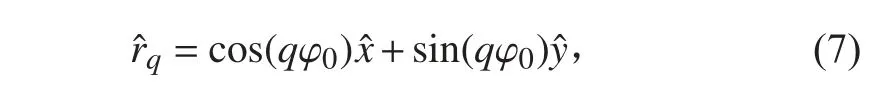
因此
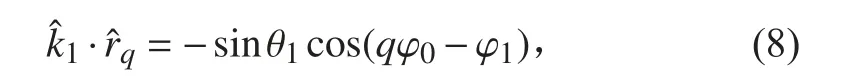
将此扩展为多个信号源(m= 1,2,···,M)
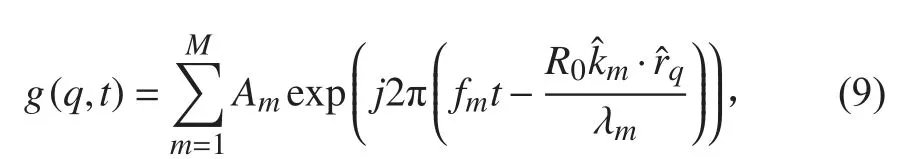
则圆阵的的导向矩阵:
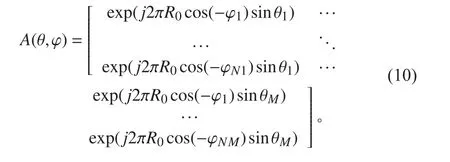
其中: φnm=nφ0-φm, θm为第m 个信号源的俯仰角,φm是 第m 信号源的方位角, R0为圆的半径。本文假设R0=0.5λ , 0 ≤ φm≤2π0,≤θm≤π/2。
1.2 线圆组合阵的数据模型
这里仅考虑由圆阵和线阵组合成三维阵列。如图2所示,圆阵位于X-Y 平面,线阵沿Z 轴排列。在特殊情况下进行研究,圆形阵列的阵元分别在X-Y 轴上,据中心阵元的距离为d,沿Z 轴的3 个阵元间距也为d。因此,阵列的7 个阵元是等间距的。
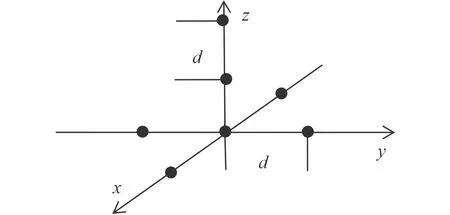
图 2 线圆组合阵Fig.2 Combination of linear and circular arrays
线性阵列3 个阵元的位置由位置矢量给出:
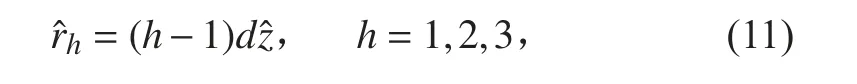
所以
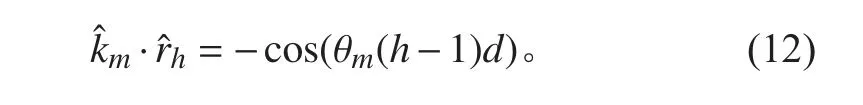
如果阵列接收M 个信号,则线性阵列的第h 个阵元的输出:
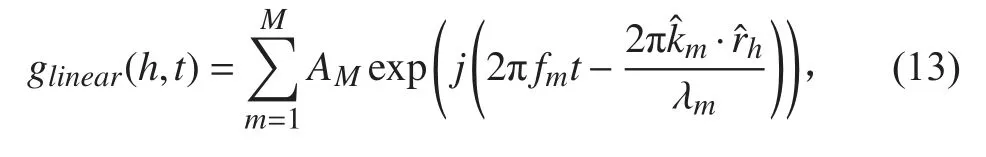
由式(8)可知圆阵的阵元输出,由此可知线圆组合阵的阵元输出为:
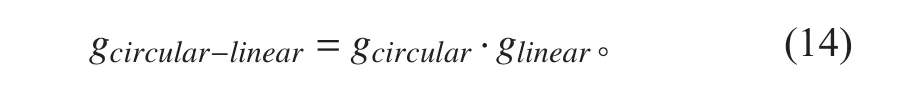
该阵列结合线形和圆形阵列,以提供二维测向。则线圆组合阵的转向矩阵:
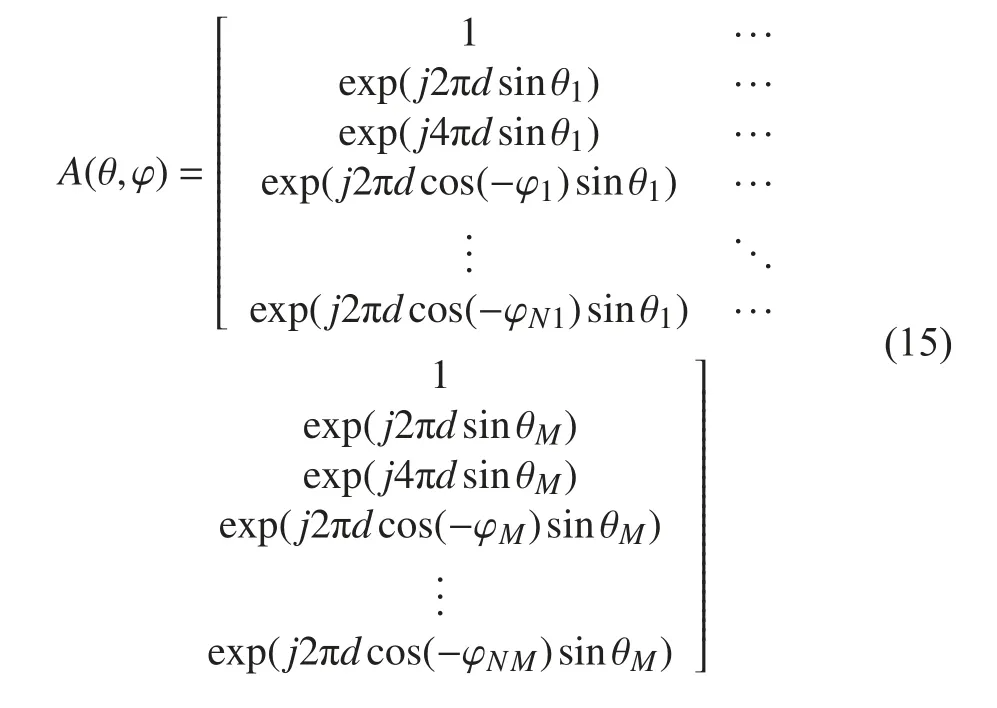
其中 d= 0.4λ,前3 行是线阵,其余为圆阵。
2 两种高分辨算法的数学模型
运用2 种高分辨定位算法估计信号的到达角:多信号分类(MUSIC)算法;最小范数(Mini-norm)算法。
2.1 MUSIC [7]
σ2对于空间理想的白噪声且噪声功率为 ,阵列数据的协方差矩阵为
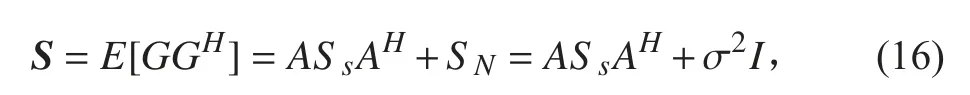
对S 进行特征分解,有
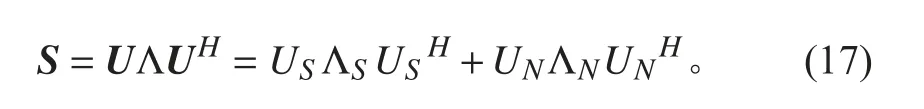
式中,U 为特征矢量矩阵,其中由特征值组成的对角阵 Λ= diag{λ1,λ2,···λM}。 利用信号子空间 US与矂声子空间 UN的正交性来估计信号的方位,所以MUSIC 的空间谱估计可表示为:
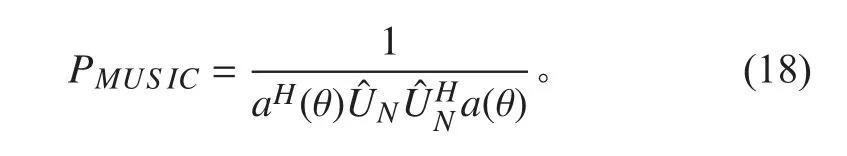
2.2 最小范数(Mini-norm)[8]
这个方法和Music 方法有些相似。其基本思想是在噪声子空间中找到特征向量的线性组合D:
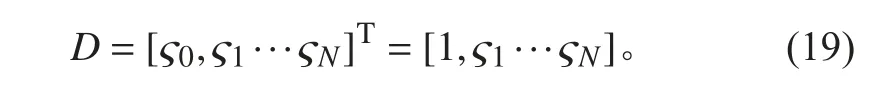
式中, ς0被指定为单位矢量。式(17)的范数的平方为:
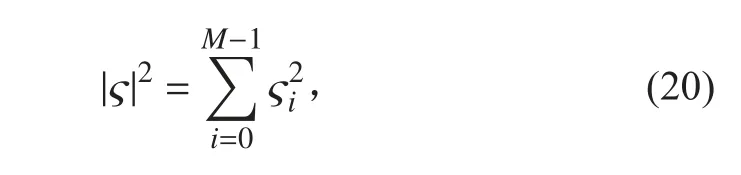
信号子空间 US可以被划分为:
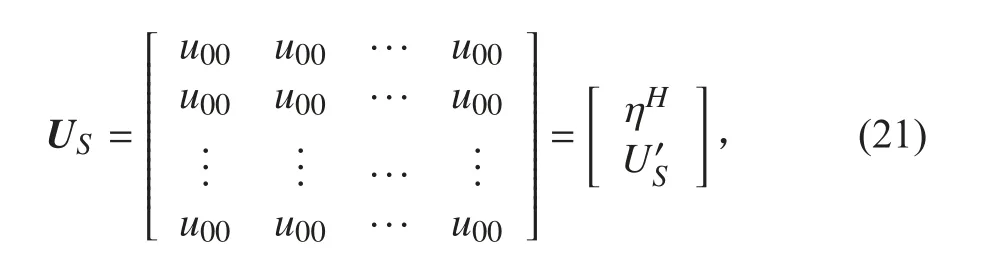
其中, ηH是 US的第一 行,是剩余 行。向量D 可以被写成
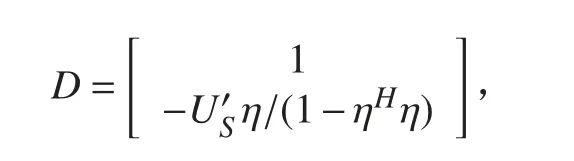
因此,最小范数[7]的空间谱估计可表示为:
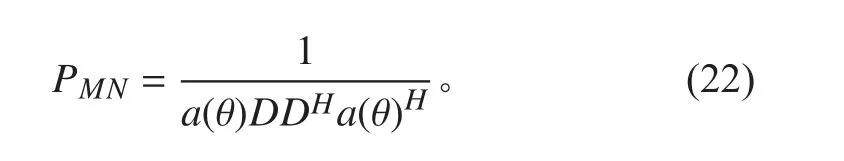
3 性能仿真与对比分析
3.1 不同信噪比的影响
考虑7 元半波长间隔均匀的圆阵和线圆组合阵,假设两等强度非相关窄带信号源分别从(16°,15°)和(21°,15°)方向入射到阵列,背景噪声与信号不相关的窄带高斯白噪声。要求分别采用Music 和MIni-norm进行目标方位估计。信噪比分别为25dB,10dB,进行仿真实验,仿真结果如图3 和图4 所示。
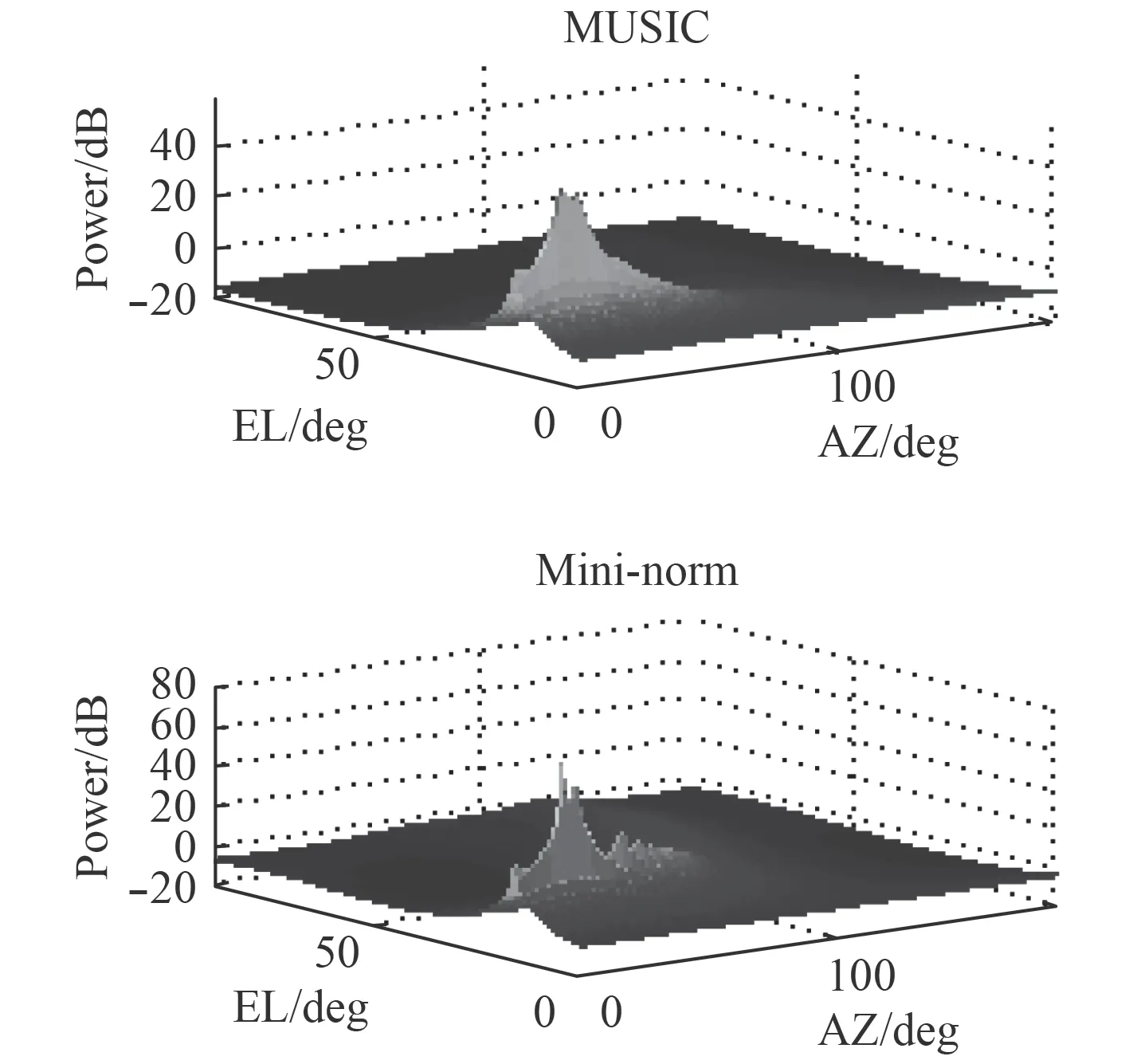
图 3 线圆组合阵,SNR=25 dBFig.3 Circular +linear array, SNR=25 dB
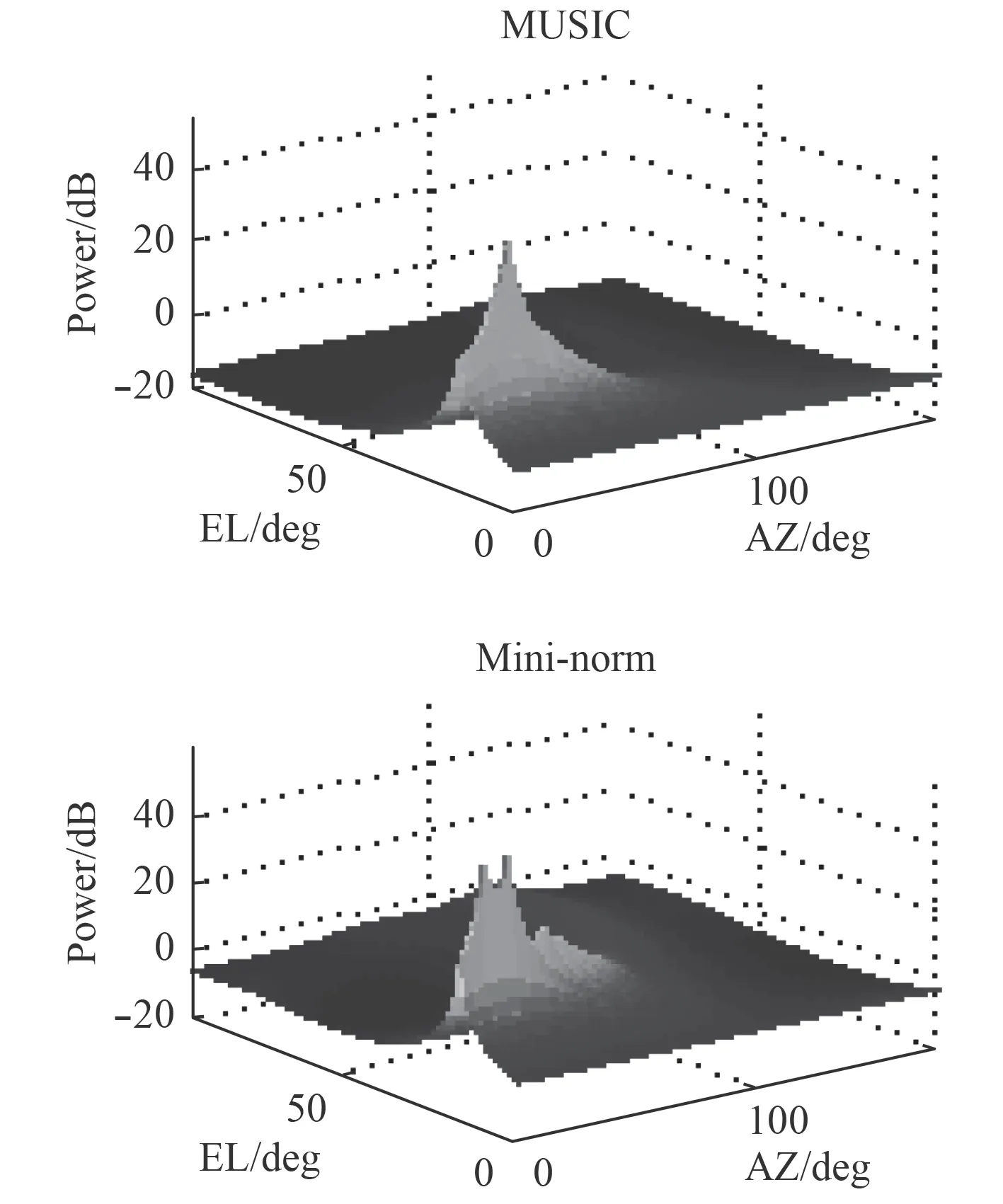
图 4 线圆组合阵,SNR=10 dBFig.4 Circular +linear array, SNR=10 dB
图3 和图4 显示了线圆组合阵在信噪比较高时,2 种算法的峰值明显,能准确定位信号源的位置。而信噪比较低时,2 种算法都失效了。图5 和图6 显示了圆阵在较高或较低信噪比时,都能定位信号源的位置,不过,在信噪比较低时,Mini-norm 算法显示的峰值更加尖锐,准确。
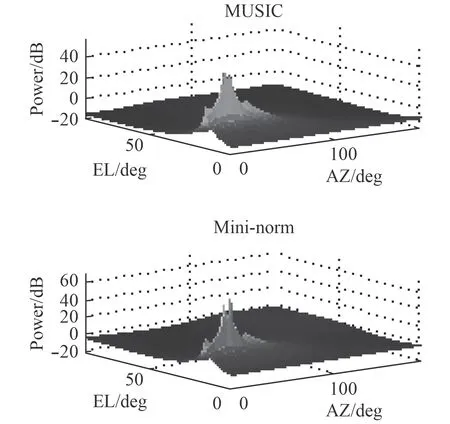
图 5 圆阵,SNR=25 dBFig.5 Circular array, SNR=25 dB
比较图3 和图5,得出在较高SNR(= 25dB)时,Music 和min-norm 方法对于2 个阵型的声源定位有相似的结果。从图4 和图6 可以看出,当SNR 较低(10dB)时,圆形阵列的效果更好。
3.2 多个噪声源影响
由各向同性的7 元阵分别组成圆阵和线圆组合阵,快拍数为4 095,4 个独立窄带远场信号,信号的方向分别为(16°,15°)、(21°,15°)、(21°,15°)(21°,15°),信噪比为25 dB, d= 0.4λ。进行仿真实验,仿真图如图7 所示。
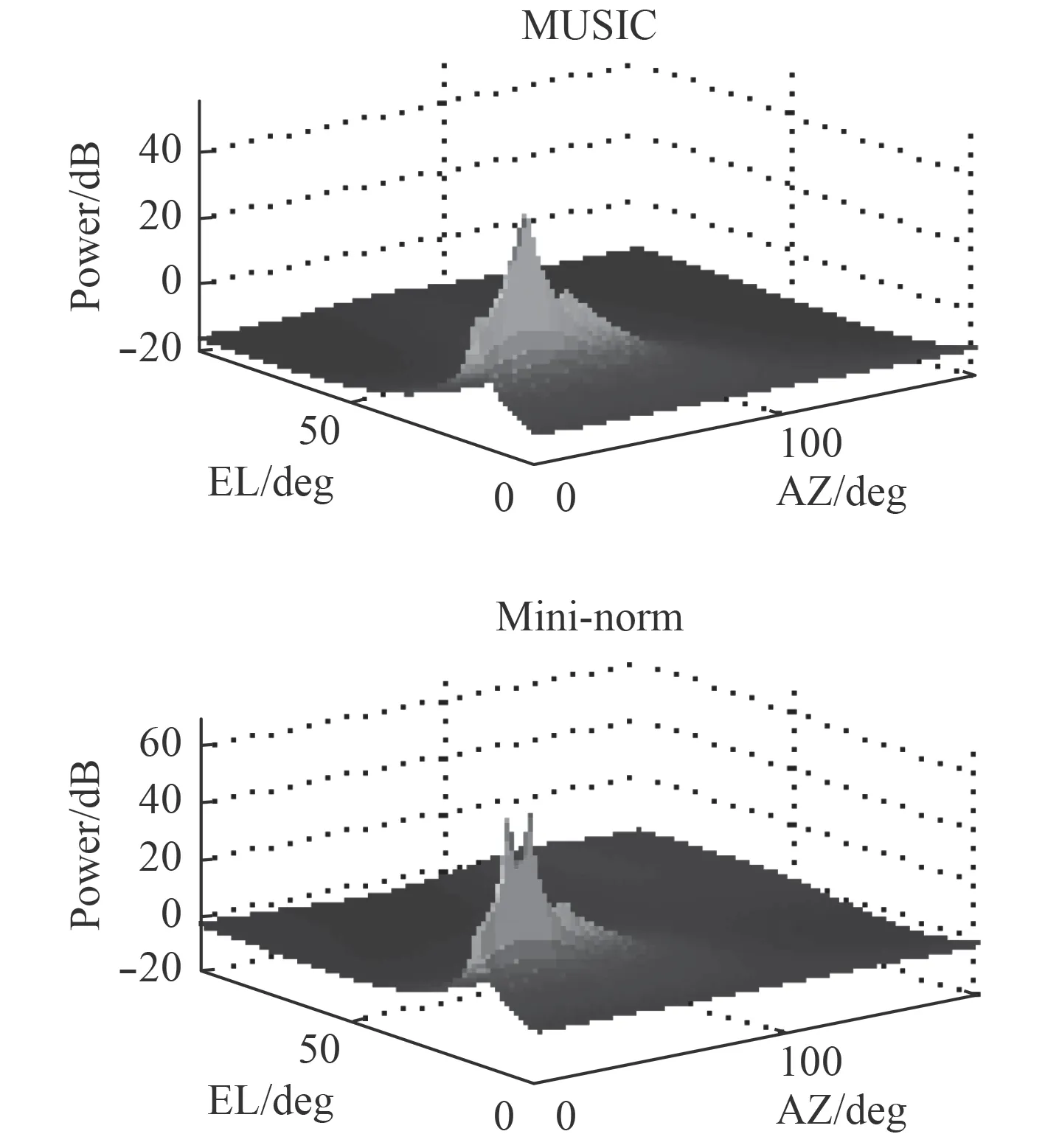
图 6 圆阵,SNR=10 dBFig.6 Circular array, SNR=10 dB
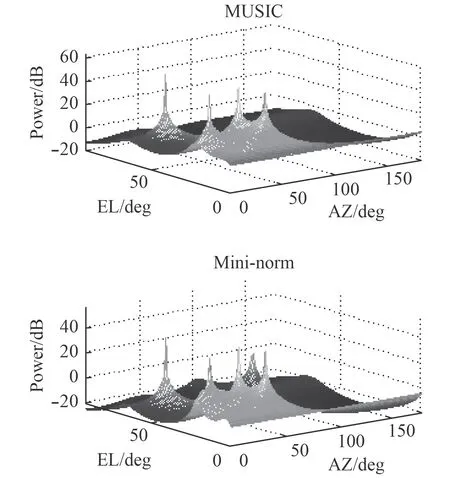
图 7 线圆组合阵,SNR=25 dBFig.7 Circular+linear array, SNR=25 dB
从图7 可以看出,多信号源时,线圆组合阵中2 种算法都可以定位信号源,但Mini-norm 算法出现了虚假峰。图8 可以看出圆形阵列可以解决4 个峰值,但圆形阵列具有更多的旁瓣。对比图7 和图8 可以得出在多信号源时,线圆组合阵和Music 算法结合能准确定位信号源的位置,且低旁瓣。
4 结 语
针对上述仿真结果,对圆阵和线圆组合阵给出以下结论:
1)在较高信噪比的情况下,2 种阵型具有相似的性能;
2)在低信噪比情况下,圆阵的性能更好;
3)圆形阵列的方位角分辨率优于线圆组合阵列的。
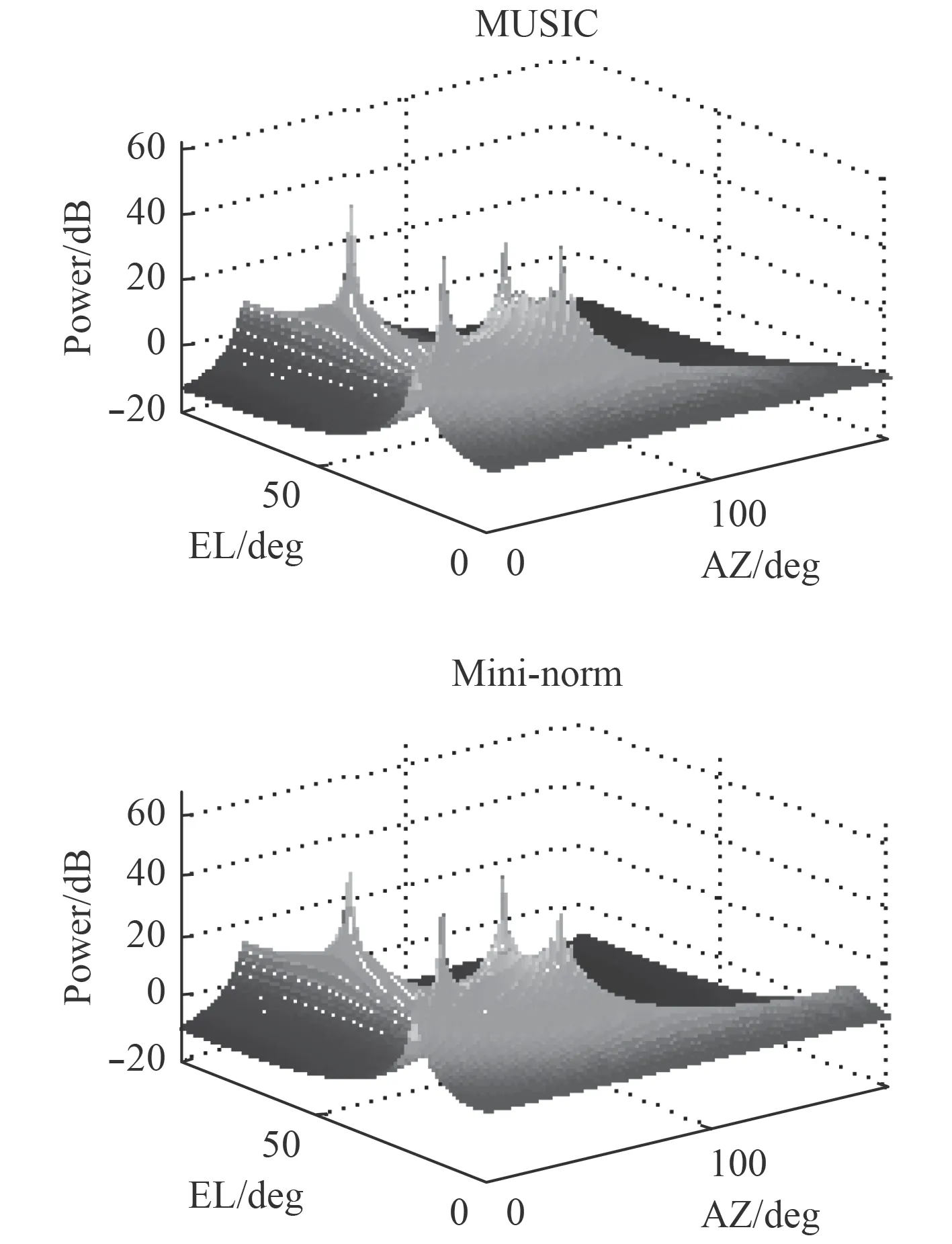
图 8 圆阵,SNR=25 dBFig.8 Circular array, SNR=25 dB
从算法来看,MUSIC 算法更稳定,几乎总是正确地显示出信号源的位置,更重要的是,低旁瓣。然而,在信噪比较低(<10 dB)的情况下,2 种阵型的music 算法都无法正确的提供峰值数目。
因此,可以得出在较低信噪比(<10 dB)时,圆阵和Mini-norm 算法组合性能最好。在多信号源时,圆阵和线圆组合阵都能定位信号源位置,但是圆阵多旁瓣,而Mini-norm 算法与线圆组合阵结合出现虚假峰。所以,在多信号源时,线圆组合阵 与Music 算法结合可以更加准确的定位信号源。
由于使用子空间方法来计算AOA,因此声源的数量必须小于阵元的数目。将来,应该考虑如何突破这种限制,以及如何在低信噪比时,提高算法的性能。
