基于四负载最小二乘法的内燃机排气噪声预测
2022-09-05刘联鋆汤汝根
韩 悦,刘联鋆,汤汝根,郑 旭,3,郑 康▲
(1.浙江大学能源工程学院,浙江 杭州 310027;2.浙江欧特立汽车空调有限公司,浙江 丽水 323000;3.浙江大学能源清洁利用国家重点实验室,浙江 杭州 310027)
0 引言
管道消声系统的声学性能取决于噪声源特性和消声器特性。内燃机的进排气系统、空调换热通风管道系统以及风机管道系统均可被考虑为管道声源系统。假设管道内声波按照平面波传播,且整个系统线性时不变,可以将管道消声系统声源看作位于管道系统管端的单端口声源[1],并将其表示为声压和阻抗的物理模型。通过准确提取的声源特性[2],可以预测管口辐射噪声以及消声器插入损失。
声源特性的提取可分为直接法[3-4]和间接法[5]。前者需要一个在所有测试频段均可提供高于被测声源声压级的外部声源,这一点对内燃机较宽的声音频率范围难以满足。后者又包含两负载法、三负载法和四负载法[6]等。通过测量声源负载截面声压(或间接测量管口声压[7]),计算管口辐射阻抗和负载阻抗可以计算声源阻抗,进一步计算声源压力。但是两负载法需要相位参考信号,三负载法和四负载法对输入误差的敏感性可能造成声源提取不准确甚至造成错误。Boden[8]提出的多负载直接最小二乘法可以在一定程度上减小该声源提取方法对输入误差的敏感性。
本文通过四负载直接最小二乘法对内燃机排气系统声源进行提取,并预测排气噪声。其中,负载的传递矩阵由基于管道平面波理论的解析法获得[9]。完整阐述该方法的理论基础、应用流程,最后通过实验验证该方法流程的有效性。
1 理论基础
给出提取内燃机排气噪声源及排气出口噪声预测方法的理论基础。
1.1 排气系统电路类比模型
可将内燃机假设为一个线性声源,整个排气系统作为负载。抽象出的管道声源负载系统如图1所示。
将该线性声源类比于电路中的恒压源,将排气系统类比于电路中的阻抗,可得到该管道声源负载系统的声电类比如图2所示。
声源与负载阻抗满足
(1)
其中,Ps、Zs分别为点声源声压和阻抗,两者均为复数量;Pl为内燃机和排气系统交界处声压;Zl为负载阻抗。
需要注意的是,关于四负载法提取声源阻抗时引入的管口辐射阻抗Zr以及管口声压pm不包含在该类比电路图中。它们是为了便于测量,将声源截面处不便测量的声压plm,借助负载传递矩阵的元素和管口声压pm计算得到αm。
1.2 排气噪声源提取
排气噪声源提取,即是对图2中Ps、Zs进行确定。首先给出四负载法提取噪声源的原理,之后在四负载法的基础上给出基于四负载的最小二乘法的提取原理。
1.2.1 四负载法
Prasad[6]于1987年首次提出四负载法间接测量声源阻抗与声压,实验及原理示意图如图3所示。
其声源提取思路如下:
根据排气系统电声类比图,得出4个负载对应的4个方程
(2)
其中,pln为布置第n个负载时,声源截面声压;Zln为第n个负载阻抗;Zs为声源阻抗;Ps为声源声压。
消掉方程(2)中声源压力项,给出如下比值
(3)
由第一个等号右侧的部分可根据声源截面测得的声压和对应负载阻抗计算α1,α2,α3。
考虑到声源负载声压测量不便,有两种办法对截面声压plm进行转换,进而求解比值αm。第一种方法,可以用管道外测得的声压值与负载传递矩阵元素表示上述比值
(4)
其中,pm为布置第m个负载时在管口测点测得的声压;Cm和Dm为第m个负载传递矩阵的元素;Zr为管口辐射阻抗。
对于圆形薄壁管端,当ka<0.5时,管口辐射阻抗[10]为:
(5)
其中,k=ω/c=2πf/c,表示波数;c为声速;a为管口半径;Y=c/S为对应于质量流量的管口特性阻抗。
第二种办法,可利用管道外测得的声压值和管口与截面传递函数,推导plm,进而计算αm。
计算得到αm后,根据式(3)第二个等号后的部分可求出声源阻抗Zs。进而,根据任意负载传递矩阵的元素或传递函数求得声源负载截面处声压,并根据式(1)求解声源声压Ps。
1.2.2 四负载最小二乘法
Boden[8]于1995年提出的多负载最小二乘法,不消去声源负载求解的非线性项,将方程(1)进行直接最小二乘获得了声源负载Zs的表达式,并通过迭代的办法获得声源参数。该方法所需要的负载压力及阻抗内容没有改变,仍然与四负载法相同,其区别仅在于优化了声源阻抗和声压的求解方法。
现将基于四负载的最小二乘法提取声源主要原理描述如下:
首先对方程(1)取模求平方
(6)
|Zs|3cTc+|Zs|2{2cos(φs)cTa+2sin(φs)cTb+cos(φs)aTc+sin(φs)bTc}+|Zs|{cTd+2cos2(φs)aTa+2sin2(φs)bTb+2sin(φs)cos(φs)aTb+2sin(φs)cos(φs)bTa}+cos(φs)aTd+sin(φs)bTd=0
(7)
其中,
(8)
(9)
(10)
(11)
式(10)中向量I为使声源阻抗平方|Zs|2满足函数f的向量性质引入的单位向量。
将相角φs在0~π内等分,代入(7)式求解,将每一组(φs,|Zs|)代入Gps表达式获得相应声源声压,将每一组(φs,|Zs|,Gps)代入函数F中,满足F最小的组合即为相应频率下的声源特性。
2 声源提取与排气噪声预测流程
给出声源排气系统管道模型声源提取以及下游出口处噪声预测的流程,如图4所示。
按照流程图所示,声源提取分两步进行,首先将计算声源截面声压和负载阻抗的准备工作通过实验、平面波法以及经验公式得到,之后应用四负载最小二乘法提取声源声压和声源阻抗。最后根据提取得到的声源特性,可以对任意负载下游声压进行预测,还可结合传递矩阵和下游声压计算插入损失,从而衡量所设计消声器性能。
该声源提取与噪声预测流程虽然是针对内燃机给出的,却适用于大多数可抽象为单管口声源的管道系统。
3 声源及排气噪声结果
3.1 内燃机实验与负载
实验用内燃机为四缸四冲程、1.6 L汽油发动机,额定功率为89 kW,额定转速为6000 r/min。发动机台架与排气口置于半消声室内,5个负载依次安装在发动机三元催化剂出口。其中负载1~4用于提取声源特性,负载5用于预测排气噪声。安装负载5时排气噪声测试现场如图5所示,负载5为一简单膨胀腔。负载两种基本形式如图6所示。
使用热电偶测量排气在负载进出口温度,监测质量流量。将声传感器布置在排气系统出口管道处,位置如图3所示,r=500 mm。测量发动机在2个稳定转速下的排气噪声,转速分别为2500 r/min、5500 r/min。
5个负载的具体尺寸列在表1中。
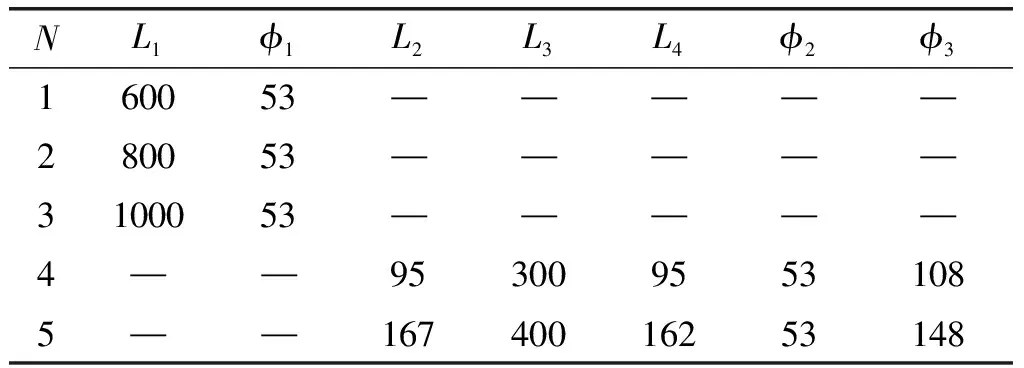
表1 负载尺寸 单位:mm
3.2 内燃机声源提取
根据实验和平面波理论计算结果,利用四负载最小二乘法提取声源声压级。此处仅给出发动机转速为2500 r/min和5500 r/min时提取的声源声压结果,如图7所示。
声源声压提取结果显示,随着转速增加,声源声压级不断升高,特别是高频噪声有较明显的提高。不同转速下,随着频率升高,噪声在下降。
给出提取得到的发动机转速为2500 r/min和5500 r/min时声源声阻如图8所示。声源声抗如图9所示。
3.3 排气噪声预测
根据提取得到的声源压力和阻抗对第5个负载出口排气声压进行预测,并与实验结果对比,发动机转速为2500 r/min时,结果如图10所示,发动机转速为5500 r/min时,结果如图11所示。
在发动机转速较低的时候,如图10所示的2500 r/min时,四负载最小二乘法预测的排气噪声与实验结果在低频较符合,但在高频差距较大。当发动机转速增大时,如图11所示的5500 r/min时,低频,即100 Hz以下结果较差,整体频段上的符合结果良好。
对于预测与实验误差的问题,可能是由于负载数目较少,导致提取的声源精度较低;也可能是由于负载1、负载2和负载3特性相近,导致关于阻抗的三次方程(7)的求解准确性降低;或者是由于在声源提取方法的引入时没有考虑平均流的影响,导致声源提取不够准确。
4 结论
本文利用四负载最小二乘法,对单端口声源管道系统声源进行提取,并根据提取的声源特性对下游管道出口声压特性进行预测。给出这一计算办法的流程方法,并用实验计算证明其有效性。
本研究对于类似的单端口声源管道系统末端降噪问题均具有参考意义,对消声器的设计提供声源特性参数,直接对安装消声器前后出口声压改善效果进行预测。
在之后的研究中,应当进一步提高声源提取的准确性和效率,进而提高噪声预测准确性。
