火星探测降落伞模型高速风洞变迎角试验技术
2020-01-14杨贤文易国庆师建元
杨贤文,郝 东,易国庆,师建元,郭 鹏
(中国空气动力研究与发展中心,绵阳 621000)
0 引 言
深空探测对带动国民经济和促进科技发展及人类发展具有重大意义,火星是太阳系中与地球最为相似的行星,美国航空航天局(NASA)、欧洲的太空局(ESA)、日本的航空航天探索局(JAXA)、俄罗斯和印度等都有关于火星探索的科研项目[1],火星探测研究在我国也受到高度重视,发展并掌握火星探测技术是国内面临的一项重要科研任务。
火星探测进入、下降与着陆(EDL)技术是火星探测的关键技术之一。尽管火星表面的大气压力不及地球表面的1%,但降落伞仍是火星探测着陆过程中最有效的一种减速工具[2]。降落伞在超声速条件下开伞使着陆器减速,当着陆器减速至低亚声速,降落伞与着陆器分离。迄今为止,美国是火星探测最成功的国家,其向火星成功发射的登陆探测器有:海盗号(Viking)[3]、火星探路者(MPF)[4-5]、火星探测漫游者(MER)[6-7]、凤凰号(PHX)[8-9]、火星科学实验室(MSL)[10-12]、洞察号(InSight),其采用的降落伞均为盘缝带伞。盘缝带伞的结构如图1所示,它的顶幅如平面圆形伞,中间开有顶孔,侧边是一个近似于圆柱形的围幅,在顶幅与侧幅之间留有较宽的缝隙,此伞稳定性较好,偏摆角一般在±5°~10°之间。盘缝带伞的阻力系数与结构透气量和下降速度等有关,约为0.4~0.7。

图1 盘缝带伞Fig.1 Disk-gap-band parachute
国内对火星探测器降落伞动力学特性进行了相关研究,高兴龙等[13]开展了火星探测器开伞过程动力学特性数值仿真研究;张青斌等[14]采用降落伞减速阶段的九自由度动力学模型,仿真分析了降落伞减速阶段火星探测器物伞系统的动力学特性,仿真过程中使用的降落伞轴向力、法向力和俯仰力矩系数采用Fluent软件计算获得,未进行风洞试验验证。为了获得火星探测器物伞系统动力学仿真中需要使用的降落伞轴向力、法向力和俯仰力矩系数,美国航空航天局兰利研究中心在TDT风洞进行了火星探测降落伞模型轴向力、法向力、俯仰力矩系数测量研究,获得了火星探测降落伞模型在马赫数范围0.1~0.3、迎角α小于15°时的轴向力、法向力和俯仰力矩系数[15]。国内以前未在高速风洞开展降落伞模型轴向力、法向力和俯仰力矩系数随迎角变化特性的试验研究,为了满足我国火星探测任务需求,中国空气动力研究与发展中心在2.4 m跨声速风洞(FL-26)开展了火星探测降落伞模型变迎角试验技术研究,进行了火星探测降落伞模型高速风洞变迎角试验,获得了火星探测降落伞模型在马赫数范围0.4~0.8、迎角范围0°~25°时的轴向力、法向力和俯仰力矩系数。本文简要介绍了研制的试验装置、数据处理与修正方法及典型试验结果。
1 模型与试验设备
1.1 模型
试验的火星探测降落伞模型为盘缝带伞,伞型结构见图1。根据透气量的不同,降落伞模型分为常规透气伞及低透气伞。降落伞模型投影面积为0.288 m2,名义面积为0.588 m2,名义直径为0.865 m,伞衣顶孔安装了一个金属圆环。
1.2 风洞
本项试验研究在FL-26跨声速风洞半模试验段中进行。FL-26风洞系试验段横截面为2.4 m×2.4 m的半回流、暂冲引射式跨声速风洞,试验马赫数范围为0.3~1.2。迎气流左侧为转窗机构壁,转窗直径为1 m。试验的火星探测降落伞模型零迎角时在风洞试验段中的堵塞度为5%。
1.3 模型支撑装置
模型支撑装置主要由前支架、后支架、风洞侧壁转盘等部件组成(见图2)。前支架主要包括主杆、上辅杆、下辅杆、前天平保护罩、前天平连接头和转子等。后支架主要包括主杆、上辅杆、下辅杆、后天平移动台、后天平连接头和载荷测量杆等。风洞试验时,降落伞模型与转子连接,转子与固定在前支架上的前测力天平相连。后天平固定在后支架上,后天平前端安装了载荷测量杆,载荷测量杆沿着降落伞模型轴线穿过伞顶孔的金属圆环,降落伞模型通过顶孔的金属圆环可以在载荷测量杆上滑动。前、后支架均固定在风洞试验段的侧壁转盘上,通过转盘转动改变载荷测量杆的迎角,即改变降落伞模型的试验迎角。

图2 模型支撑装置示意图Fig.2 Schematic of the model test fixture
1.4 天平
测量降落伞模型气动力和力矩的前、后天平为六分量电阻应变天平。
2 数据处理与修正
试验过程中,对天平测力结果及流场参数进行连续采集,采样频率300 Hz,本文给出的气动力系数测值为流场稳定阶段气动力系数连续采集结果取平均获得,并对暴露在气流中的转子等部件的附加气动力、支撑干扰及洞壁干扰进行了扣除修正。通过不安装降落伞模型的风洞试验可以直接获得暴露在气流中的转子等部件的附加气动力。
2.1 支撑干扰修正
支撑阻力干扰因子Kαs表示如下[15]:
Kαs=1+KαKs
(1)
式中:Kα为支撑装置迎角对阻力的影响系数,Ks为0°迎角时支撑阻力干扰因子。
Kα为不同迎角时支撑装置前支架沿气流方向在降落伞模型上投影面积与0°迎角时前支架投影面积的比值[15]。本项试验研究中,根据支架外形及降落伞模型几何外形可得:α=0°,Kα=1.0;α=2.5°,Kα=0.96;α=5°,Kα=0.8;α=7.5°,Kα=0.48;α=10°~25°,Kα=0。
选用标准κ-ε湍流模型,采用有限体积法求解N-S方程,分别计算0°迎角降落伞模型前方有、无支撑装置时的阻力系数,通过式(2)获得0°迎角时支撑阻力干扰因子Ks,图3、图4分别给出了有、无支撑装置的降落伞模型阻力特性计算网格图,计算结果见表1。
(2)

图3 有前支架的计算网格图Fig.3 Computational grid of parachute model with front truss
图4 无前支架的计算网格图Fig.4 Computational grid of parachute model without front truss

表1 支撑阻力干扰因子KαsTable 1 Strut drag interference factor Kαs
2.2 洞壁干扰修正
2.2.1实壁洞壁
降落伞在大气中工作是无洞壁约束的,风洞试验时,风洞洞壁的存在使绕降落伞模型的流场发生改变。采用有限体积法求解N-S方程,分别计算有、无风洞实壁洞壁约束时降落伞模型的阻力系数,通过式(3)获得风洞实壁洞壁干扰引起的速压修正因子Kq实壁,图5给出了无风洞实壁洞壁状态的计算网格图,去掉风洞实壁洞壁外的计算网格可以获得风洞实壁洞壁状态的计算网格,这样做可以抵消掉有、无风洞实壁洞壁约束计算时由于网格生成的差异引起的误差。
(3)

图5 无风洞实壁洞壁时的计算网格图Fig.5 Computational grid of parachute model in a freE-air boundary condition
2.2.2透气壁洞壁
参考文献[16]给出了速压修正因子随模型堵塞度及洞壁开闭比变化的规律(见图6),参考文献[17]给出了透气壁速压修正随Ma变化较小的研究结果。FL-26跨声速风洞半模试验段洞壁为综合开孔率4.8%的透气壁,本项试验研究中,依据上述求解N-S方程获得的实壁洞壁干扰引起的速压修正因子Kq实壁及图6给出的开闭比对洞壁干扰影响规律进行插值计算,计算得到FL-26跨声速风洞半模试验段洞壁干扰引起的速压修正因子Kq:Ma=0.4和Ma=0.6时,Kq=1.04;Ma=0.8时,Kq=1.05。
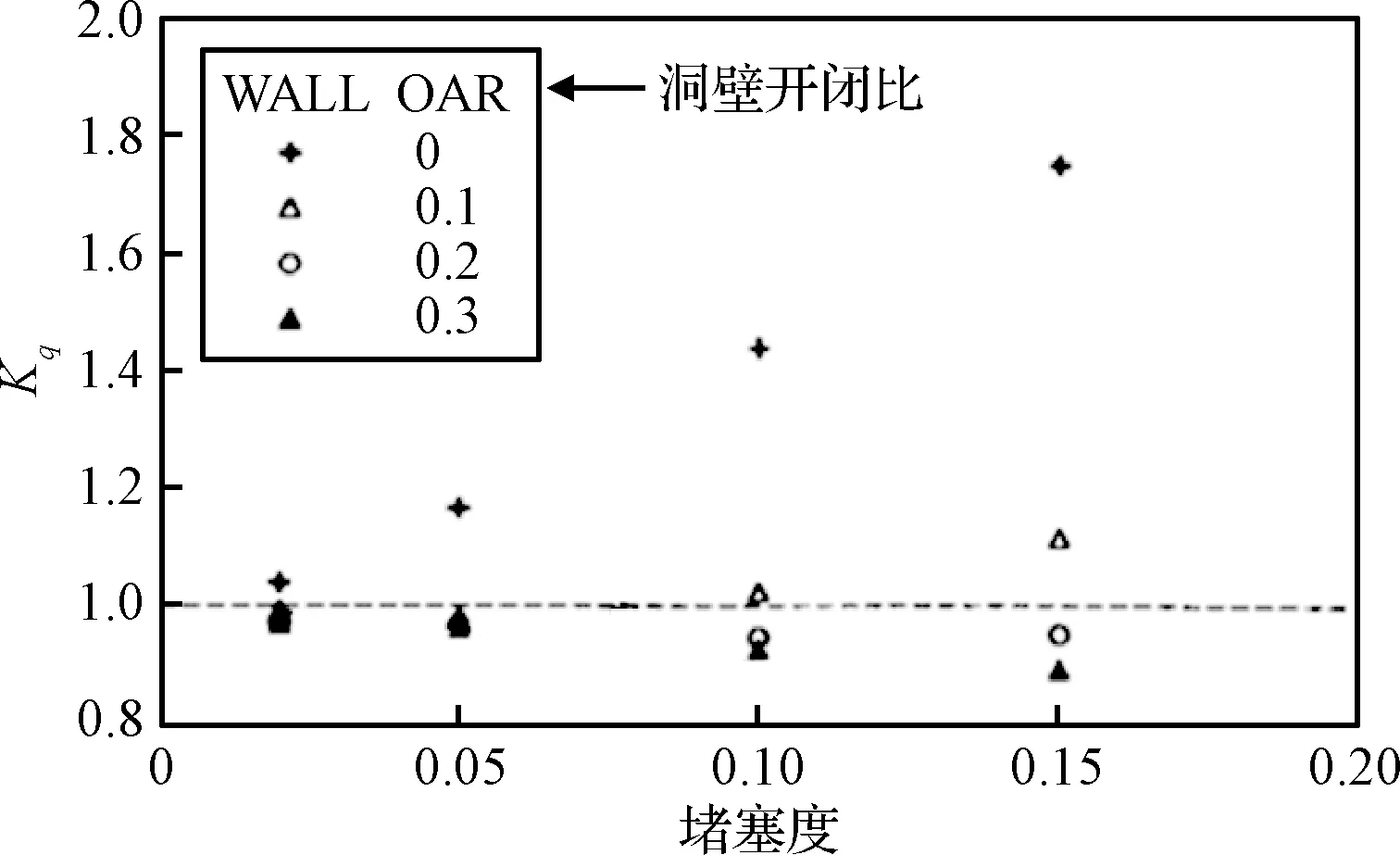
图6 模型堵塞度及洞壁开闭比对速压修正因子的影响Fig.6 Model blockage correction as a function of geometric blockage ratio and wall open area ratio
此外,若在模型测力的同时,测出透气壁洞壁附近的压力分布,作为透气壁洞壁的边界条件,采用有限体积法求解N-S方程,可以获得风洞透气壁洞壁约束条件下的模型阻力系数,再以远场边界条件计算无风洞洞壁约束条件下的模型阻力系数,二者之比即是透气壁洞壁干扰引起的速压修正因子Kq。本项试验研究中,未进行壁压测量,故未采用上述壁压信息法计算风洞透气壁洞壁干扰引起的速压修正因子Kq。
2.3 气动力系数计算
对风洞试验中的降落伞模型气动力进行分析[15],如图7所示,N1,N2分别为前、后天平测得的法向力,T1,T2分别为前、后天平测得的轴向力,MZ2为后天平测得的俯仰力矩。
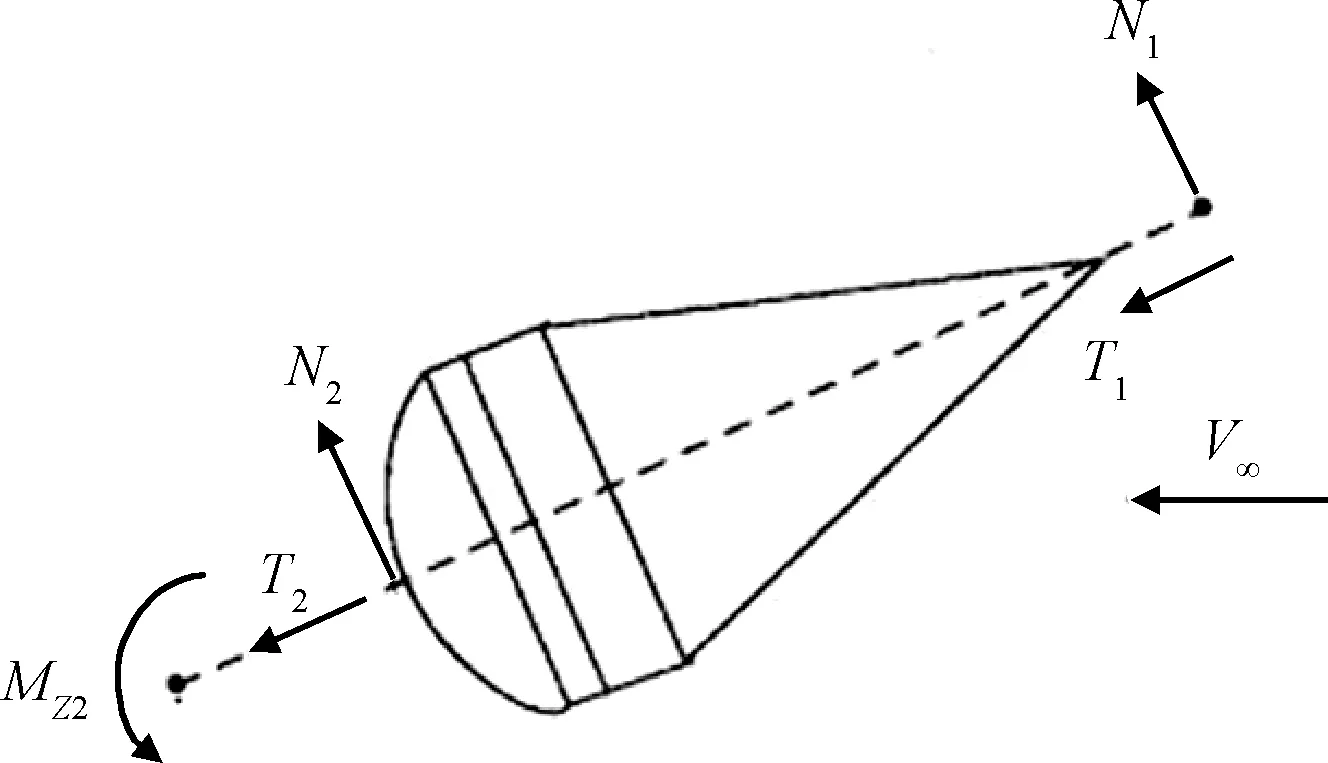
图7 前、后天平测力示意图Fig.7 Schematic of force and moment components measured by front and rear wind tunnel balances
降落伞模型轴向力系数为:
(4)
式中:Kαs为支撑阻力干扰因子,Kq为洞壁干扰引起的速压修正因子,q为来流速压,A0为降落伞模型名义面积。
降落伞模型法向力系数为
(5)
如图8所示,A,E分别为前、后天平的校心,B为伞绳汇结点,D为降落伞对载荷测量杆施力的作用点,C为降落伞的压力中心。
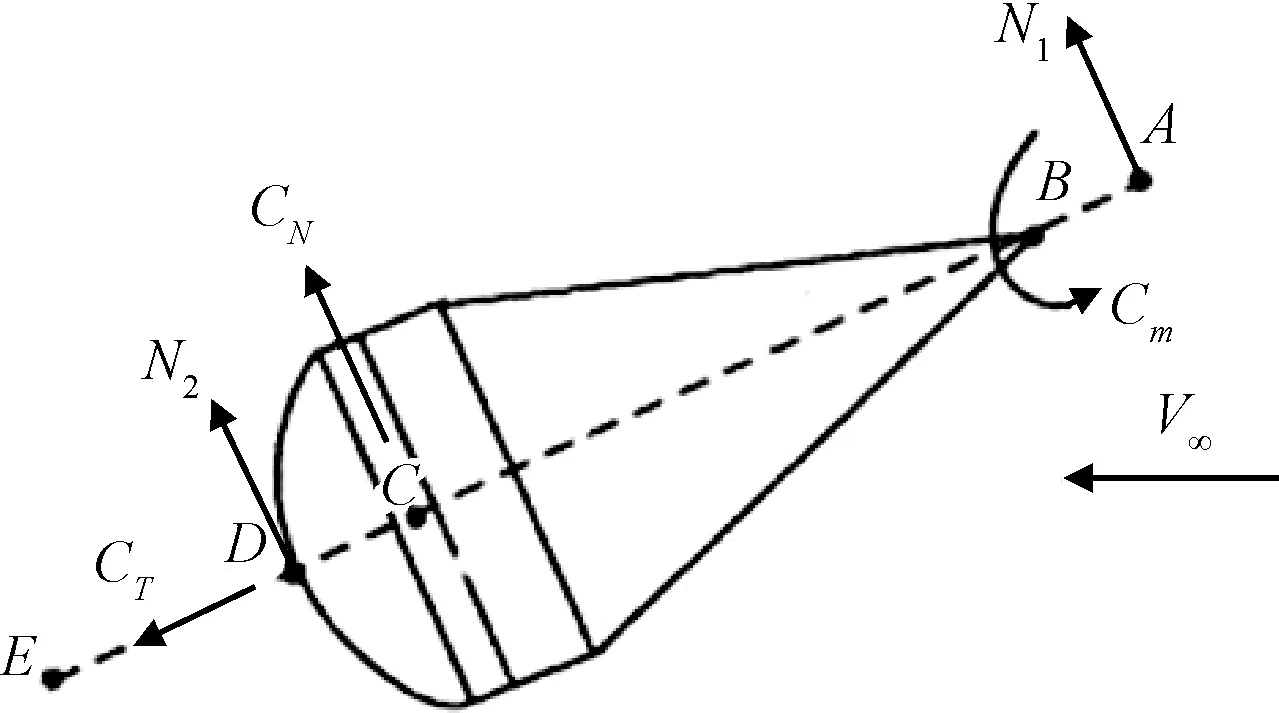
图8 气动力系数测量示意图Fig.8 Schematic of aerodynamic coefficient measurement
(6)
(7)
取伞绳汇结点B为力矩参考点,则降落伞模型的俯仰力矩系数按式(8)计算,其中,D0为降落伞模型的名义直径。
(8)
3 典型试验结果
3.1 轴向力特性
图9给出了火星探测降落伞模型的轴向力系数随迎角的变化曲线。降落伞模型的轴向力系数随迎角变化较小,在Ma=0.4和Ma=0.6时,低透气伞轴向力系数较常规透气伞增大,在Ma=0.8时,低透气伞轴向力系数较常规透气伞减小。

图9 降落伞模型轴向力系数随迎角的变化曲线Fig.9 Axial force coefficient versus angles of attack for model parachute
3.2 法向力特性
图10为火星探测降落伞模型的法向力系数随迎角的变化曲线。常规透气伞的法向力系数随迎角增大而增大,在Ma=0.4和Ma=0.6时,低透气伞的法向力系数在小迎角时随迎角增大而减小;低透气伞的法向力系数较常规透气伞减小,这可能是由于低透气伞上半部分伞衣外表面绕流较常规透气伞更易发生流动分离所致。

图10 降落伞模型法向力系数随迎角的变化曲线Fig.10 Normal force coefficient versus angles of attack for model parachute
3.3 静稳定特性
图11为火星探测降落伞模型的俯仰力矩系数随迎角的变化曲线。在Ma=0.4~0.8时,常规透气伞静稳定,在Ma=0.4和Ma=0.6时,低透气伞在零迎角时静不稳定,出现了非零配平迎角(降落伞模型Cm=0且dCm/dα<0对应的迎角为配平迎角,见参考文献[15])。低透气伞的静稳定性较常规透气伞减小,这是由于低透气伞的法向力系数较常规透气伞减小所致。
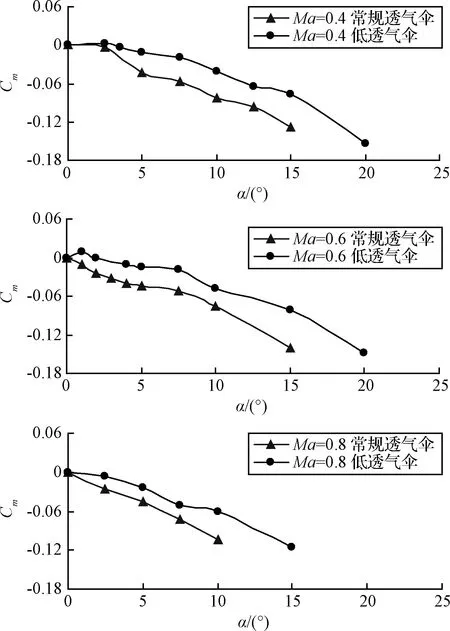
图11 降落伞模型俯仰力矩系数随迎角的变化曲线Fig.11 Pitching moment coefficient versus angles of attack for model parachute
3.4 伞衣塌陷迎角
常规透气伞下半部分伞衣在Ma=0.4~0.6、α=20°及Ma=0.8、α=15°时出现塌陷,低透气伞下半部分伞衣在Ma=0.4~0.6、α=25°及Ma=0.8、α=20°时出现塌陷,这是由于迎角较大时,下半部分伞衣的内表面压力低于其外表面压力所致。
4 结 论
通过本项研究,得出以下结论:
1)建立的火星探测降落伞模型高速风洞变迎角试验技术已成功应用于火星探测降落伞模型轴向力、法向力和俯仰力矩系数测量,该技术也适用于其它类型降落伞模型。
2)火星探测降落伞模型的轴向力系数随迎角变化较小。
3)常规透气伞的法向力系数随迎角增大而增大,在Ma=0.4和Ma=0.6时,低透气伞的法向力系数在小迎角时随迎角增大而减小,低透气伞的法向力系数较常规透气伞减小。
4)在Ma=0.4~0.8时,常规透气伞静稳定,低透气伞的静稳定性较常规透气伞减小,在Ma=0.4和Ma=0.6时,低透气伞在零迎角时静不稳定,出现了非零配平迎角。
5)在较大迎角时,火星探测降落伞模型下半部分伞衣出现塌陷。
