基于凯恩法三柱塞式乳化液泵连杆惯性力的研究
2020-01-13杨文斌付莎莎
杨文斌,李 晶,付莎莎
(西安工程大学 机电工程学院,陕西 西安 710048)
0 引 言
乳化液泵站是煤矿开采的重要设备,乳化液是煤矿综采工作面中液压支架和单体支柱的液压传动介质。乳化液泵性能直接决定着泵站的工作效率[1-2]。乳化液泵驱动系统的主要结构是曲柄滑块机构。这种机构由若干刚性构件用低副(回转副、移动副)联接而成。国内外许多学者通过建立各种数学模型,研究了曲柄滑块机构的动力学特性。刘俊[3]、史雷鸣等[4]建立了曲柄滑块机构的数学模型,通过Simulink与ADAMS软件的仿真比较,研究了滑块的动力学特性。对于曲柄滑块机构的惯性力,文献[5-7]从理论上分析了摩托车发动机曲柄连杆机构的二阶惯性力,并给出了惯性力调整方法。
目前,对于曲柄滑块机构的研究大多停留在对单个机构的动力学研究。如今大多使用三柱塞乳化液泵,动力学特性较单柱塞的复杂。当前,对于三柱塞乳化液泵的研究,主要靠计算机仿真和利用单柱塞研究成果进行经验设计[8-10],缺乏理论上的支撑和数学模型计算。关于曲柄滑块机构的惯性力研究,Christoloukas等[11]在Visual Basic Net编程包下,面向对象编程模块,建立了运动学和动力学分析的精确方程,开发了理论动态仿真软件。利用该软件可以仿真曲柄滑块机构各个杆件的惯性力,但并未深入探讨影响各杆件惯性力的因素。
凯恩法[12-13]是一种处理非完整系统的经典方法。凯恩方程将矢量形式的力和达朗贝尔惯性力沿某些特殊的基矢量投影,因而具有矢量力学的特点。凯恩方程的优点是便于处理非完整系统或有多余约束的完整系统,包括带多余铰非树系统。对此类系统,只需令广义速率超过系统的自由度,利用补充列出约束条件小区多余广义速率,即可导出与独立广义速率对应的动力学方程。本文利用凯恩法建立乳化液泵曲柄滑块机构的动力学模型,利用三柱塞式乳化液泵的结构有均匀相位差(相位差为120°)的特点,对动力学模型进行改进,得到三柱塞乳化液泵连杆的惯性力计算方法。文中还根据凯恩法得到的数学模型分析曲柄连杆长度之比值及曲轴输入角速度对连杆惯性力的影响,为设计高性能的连杆提供参考。
1 建立数学模型
1.1 坐标系与状态量定义
为了便于分析,绘制三柱塞乳化液泵的机构简图,如图1所示。

图1 三柱塞乳化液泵曲轴系的机构简图
建立定参考系(O-x0y0z0),原点与O1重合。图1中各个参数代表的意义如下:l1,l2分别为曲柄与连杆长度(mm);O1,O2,O3为旋转铰;φ1,φ2,φ3为曲柄转过的角度(°);ψ1,ψ2,ψ3为连杆与水平面的夹角(这里取锐角)(°);x1,x2,x3为滑块的水平位移(mm)。

1.2 广义速率选取
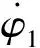
(1)
运动学约束条件
(2)
化作对广义速率的约束条件
(3)
设a1为独立变量,解出多余变量b1,c1为a1的函数
(4)
用广义速率表示各分体的质心速度:
(5)
由式(5)得到与a1对应的第一偏速度
(6)
设连杆的质量为m2,连杆上作用的惯性力的主矢为
(7)
1.3 计算对应连杆的广义惯性力
不考虑广义惯性力矩,连杆广义惯性力为
(8)
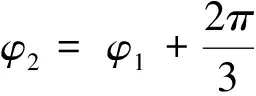
2 仿真对比验证
2.1 MATLAB数值仿真
为了进一步提高该泵的运转性能,在建立了复杂的数学模型后,通过MATLAB编程[14],使函数表达式通过曲线图直观地表现出来。将乳化液泵曲轴系统的结构参数(表1)代入方程(7)中,建立M文件。
表1乳化液泵曲轴系统的结构参数
Table 1 Parameters of the emulsion pump crankshaft system

零件质量/kg杆长/mm质心到铰点的距离 /mm密度/(kg·mm-3)转动惯量/(kg·mm2)曲轴3030159×103连杆502201107.8×10-62×105柱塞20
将所建立的M文件经过编译和调试后,得到乳化液泵曲轴系统连杆的间接惯性力曲线图。根据凯恩方程得出的三柱塞乳化液泵连杆的惯性力曲线,相邻曲线的相位差为120°,惯性力的大小随曲轴的转动呈现周期性的变化。图2为一个周期惯性力(用加速度a表示)随时间t变化曲线图。
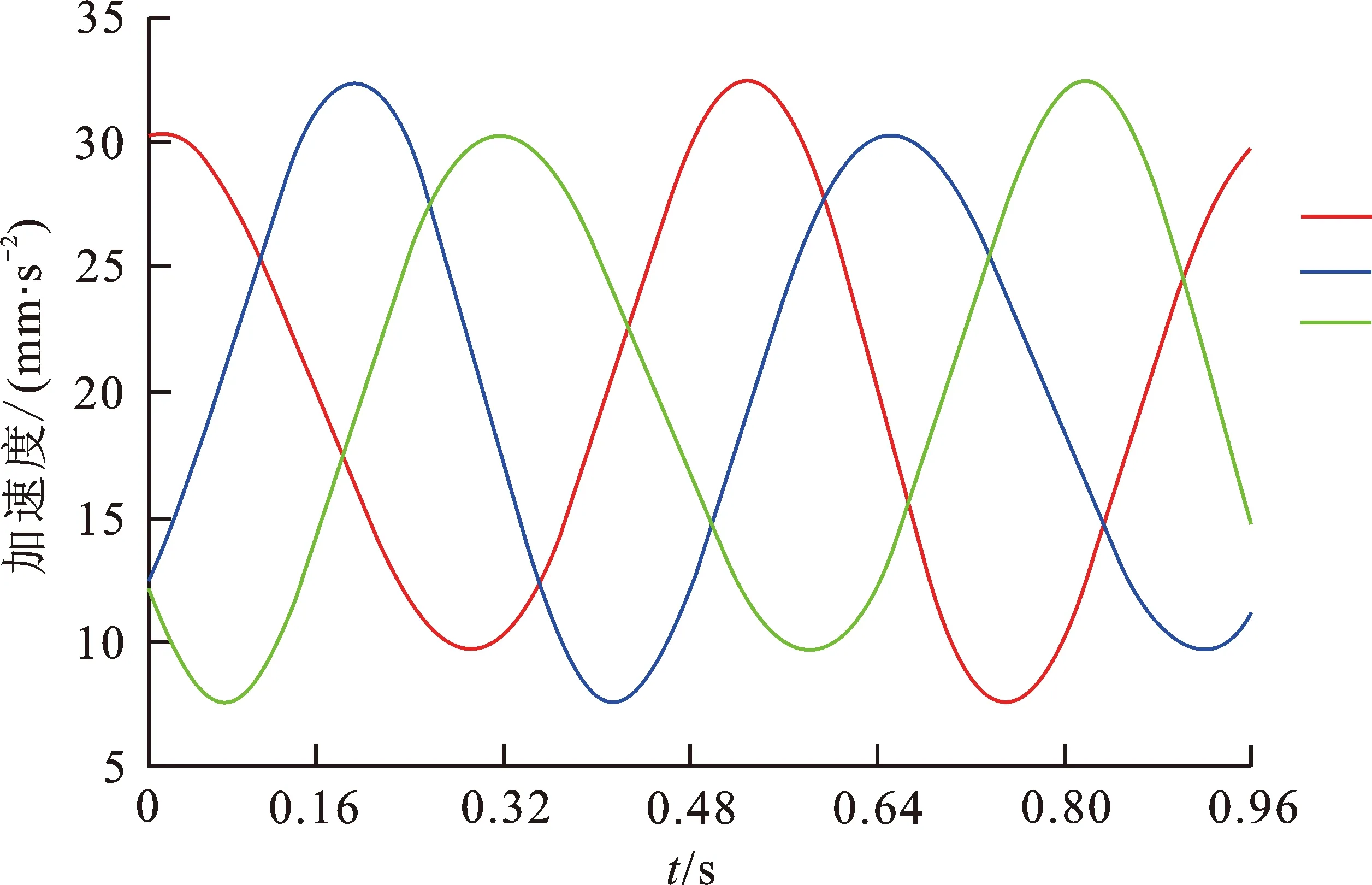
图2 曲轴驱动系统连杆质心的加速度曲线
2.2 ADAMS建模及仿真
三柱塞乳化液泵三维模型如图3。利用Solidworks软件建立三柱塞式乳化液泵实体模型,然后以 .x_t格式导入ADAMS中进行动力学分析[15]。
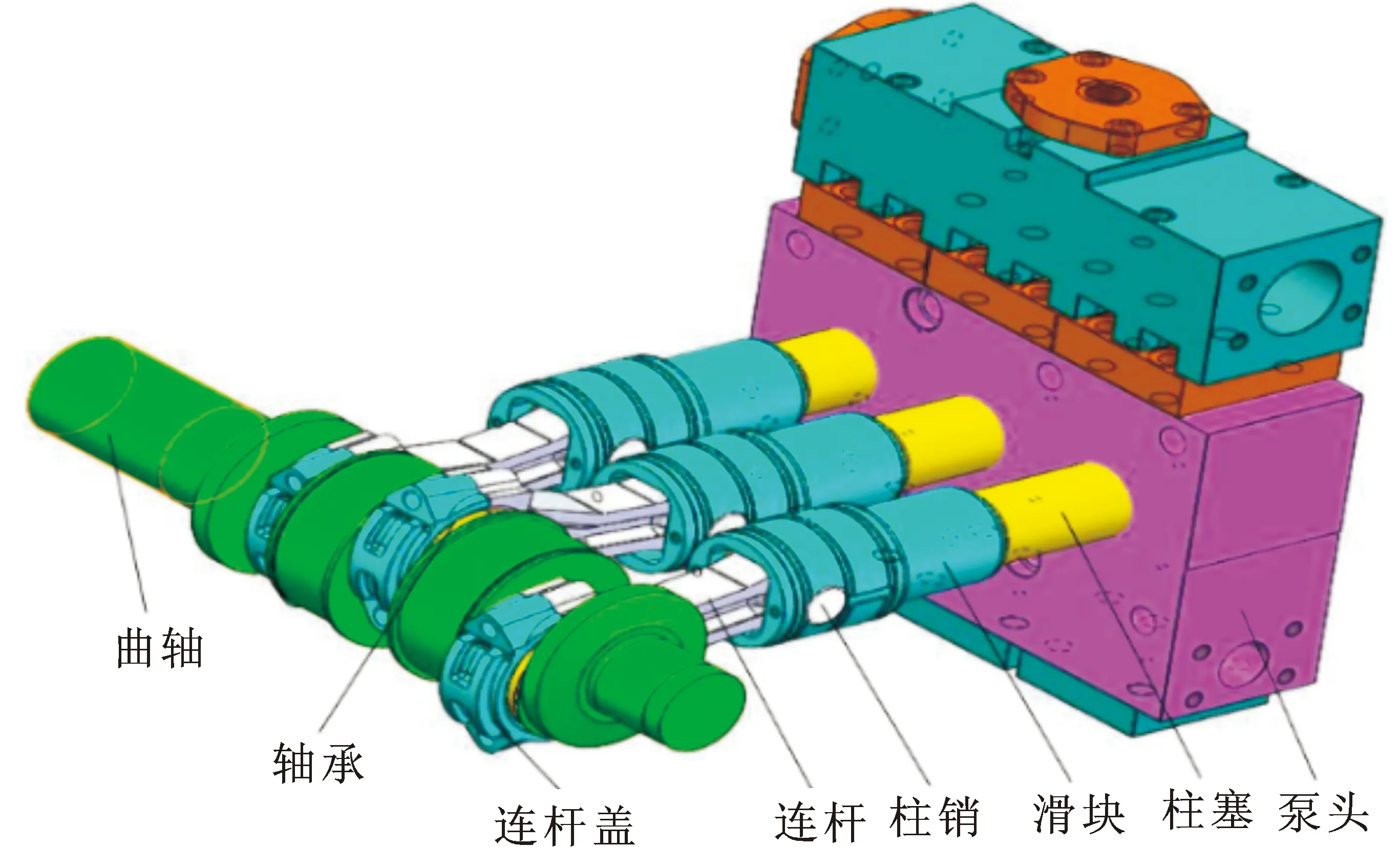
图3 三柱塞乳化液泵三维模型
为减小仿真分析的复杂度,忽略一些次要因素,将分离式的连杆组件看作一体式结构,降低了模型复杂度。在ADAMS软件中将分离的连杆、柱塞滑块组件分别进行布尔合并操作。乳化液泵各个部件之间的运动副关系如表2。

表2 各连接部件的运动副
设置各个部件的运动副关系后,需要设置驱动方式及大小。对于驱动方式,在ADAMS中通常有3种类型,分别是位移、速度、加速度。选用速度驱动的方式,驱动加在曲轴-大地运动副上,驱动函数2π rad/s表示曲轴保持2π rad/s的常值匀速转动。
乳化液泵机械结构部分主要受乳化液液压力的影响,该力方向垂直于柱塞端面,并且指向柱塞。当柱塞处于吸液阶段时,柱塞力为吸入压力;当柱塞处于排液阶段,柱塞力为排出压力。通过对比,排出压力远大于吸入压力,因此在实际计算中吸入压力可以忽略不计[16]。文献[17]在研究工作面支架液压系统时,测试了1 000 s内泵的压力数据。从数据中可以看出,泵处于加载状态时,柱塞压力可近似地认为按照正弦规律变化,用来近似模拟乳化液泵受到的液压力。张利峰[18]对某一型号的乳化液泵进行动力学分析,得到三柱塞乳化液泵的柱塞所受力大小的曲线。
对于三柱塞式乳化液泵,相邻曲拐之间有120°的相位差,而且每个柱塞的结构大小相同,所以每个柱塞受到的外载荷也呈现120°的相位差。根据柱塞所受力曲线的变化,可以近似拟合出3个柱塞受力的方程:
F1=221 432·sin(96.7t)+253 066
F2=221 432·sin(96.7t+2.09)+253 066
F3=221 432·sin(96.7t+4.18)+253 066
在额定工况下,利用ADAMS软件对乳化液泵曲轴系模型做多体动力学分析,得到连杆的加速度曲线图,如图4。加速度的变化规律间接地反映了杆件惯性力的变化[19]。
由图2,4知,连杆的加速度呈现周期性的变化。曲拐Ⅱ的加速度曲线相对于曲拐Ⅰ滞后120°,这是由于曲拐的特殊结构(相邻单曲拐轴线之间的关于曲轴轴线的转动角为120°)造成的。同理,连杆Ⅲ的加速度曲线相对于连杆Ⅱ也滞后120°。
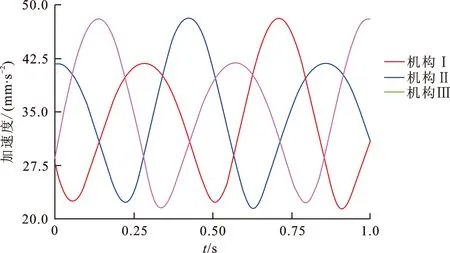
图4 连杆质心加速度曲线
3 惯性力影响因素分析
根据凯恩法,将乳化液泵的结构参数代入式(7),得到连杆惯性力的计算公式。对于三柱塞的乳化液泵连杆,其运动是平面运动。根据刚体平面运动的性质,连杆的运动可分解为平移运动和旋转运动,平移运动中影响惯性力的主要因素是质量与加速度;旋转运动中影响惯性力的主要因素是转动惯量与角加速度;曲柄的驱动角速度、滑块移动速度等也会对连杆的惯性力产生影响。以上这些因素主要由曲柄的角速度与机构的总体尺寸共同决定,本文重点考虑曲柄角速度和机构尺寸对惯性力的影响。考虑了曲柄与连杆长度比λ和曲轴驱动角速度ω对连杆惯性力的影响。利用MATLAB编写程序进行仿真,得到上述参数的变化对三柱塞式乳化液泵惯性力大小的影响。
3.1 λ对惯性力的影响
λ的大小随连杆长度变化而改变。为便于分析,本文作如下假设:
(1)曲柄长度l1不变。
(3)连杆选用同一材质,在非惯性系中,刚体连杆惯性力主矢遵循动力学规律:
F=ma
(9)
式中:m为连杆质量;a为刚体移动加速度。
λ改变时,连杆质量发生变化,由式(7)可知,λ的大小同样影响连杆的移动加速度。即根据式(9)分析连杆加速度时,要同时考虑λ对m,a的影响。
根据假设条件和λ=l1/l2,λ与连杆质量成反比。由式(7)分析加速度可以得到,λ增加,连杆质心加速度增加,惯性力增加。取λ1=0.25,λ2=0.30,λ3=0.35综合分析,得到图5的变化曲线。
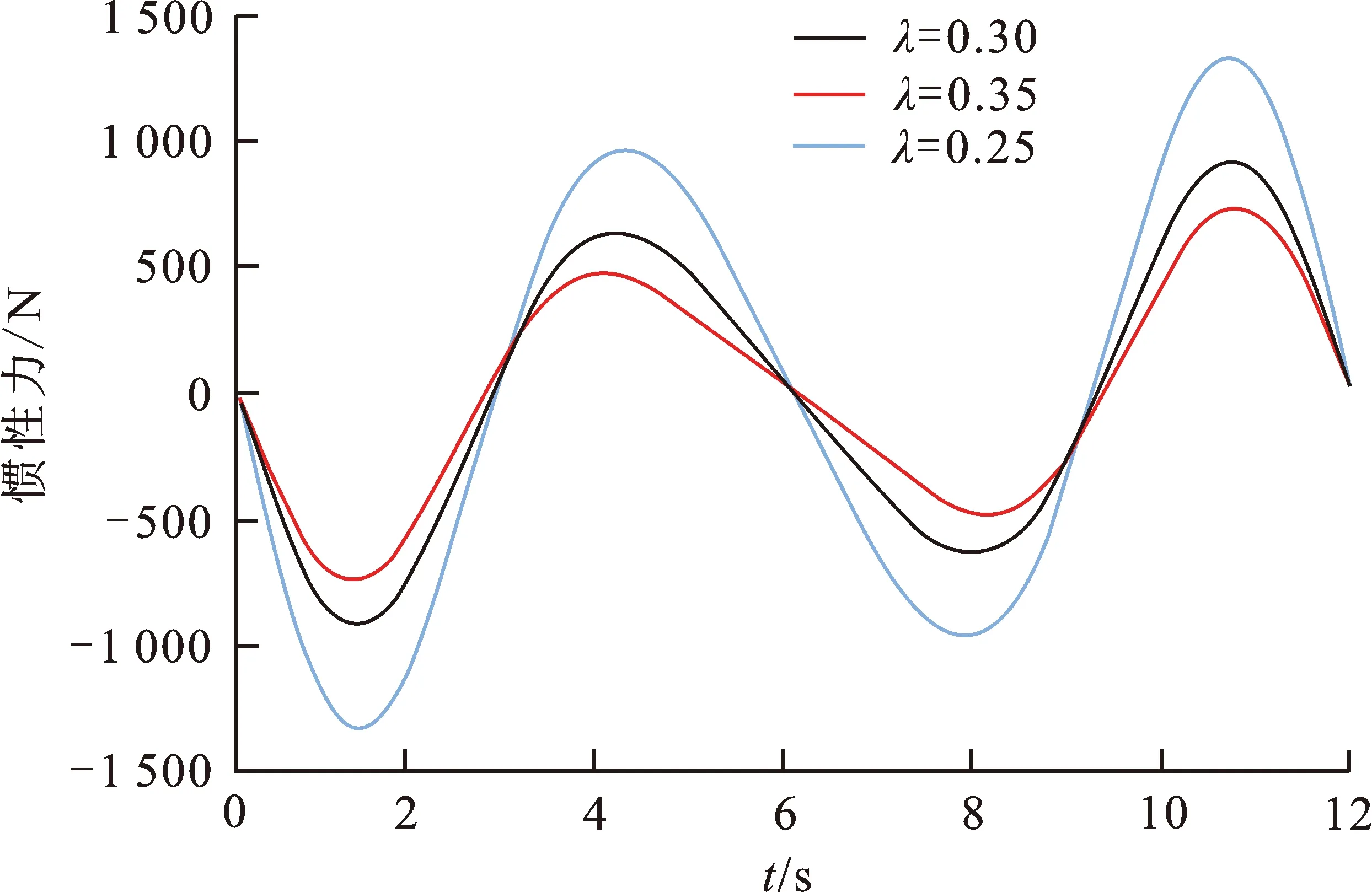
图5 λ对连杆惯性力的影响
由图5可知,连杆的惯性力随着时间出现周期性的变化,这是由连杆加速度在运动过程中的周期性变化决定的。λ改变对连杆惯性力变化的幅值有显著的影响。λ增大,惯性力的幅值减小。原因是λ对连杆质量的影响大于λ对连杆质心加速度的影响,从而导致连杆惯性力减小。
3.2 驱动角速度ω对惯性力的影响
根据式(7),曲轴的驱动转速对连杆惯性力的大小有显著的影响。图6为连杆惯性力大小随曲轴驱动角速度的变化曲线。从图6可以看出,随着驱动角速度的增加,连杆的惯性力出现振荡,而且振荡幅值会越来越大。
将曲线每个极值(见图6)所对应的曲轴角速度设为ω1,ω2,ω3,ω4,ω5,…。令Δω1=ω2-ω1,Δω2=ω3-ω2,…,Δωi=ωi+1-ωi(i=1,2,3,…)。令相邻惯性力峰值之间的时间差为ΔTi,
(10)
由图6可以看出,Δω1>Δω2>…>Δωi;根据式(10),ΔT1>ΔT2>…>ΔTi。所以随着角速度的增大,惯性力振荡频率也增大。

图6 曲轴驱动角速度变化对连杆惯性力的影响
4 结 论
(1)利用凯恩法建立乳化液泵曲轴驱动系统的动力学方程,得到连杆质心加速度的变化曲线,与 ADAMS仿真分析得到的连杆的加速度特性对比,得出两者的变化曲线基本吻合。
(2)应用凯恩法分析连杆惯性力的影响因素。在达到乳化液泵工况要求的情况下,λ增大时,连杆惯性力减小。这是由于λ对质量的影响要大于对质心加速度的影响。但是,λ值过大,连杆的角加速度增大,从而连杆的惯性力矩增大。
(3)曲轴驱动速度ω不宜过大。ω增加,连杆惯性力变化频率与幅值会显著增加。
研究限于篇幅,没有考虑连杆的惯性力矩。另外在分析时,将连杆等效为刚体,未考虑其柔性,需进一步研究。
