一种基于非线性尺度空间的ORB特征匹配算法研究

郭 芮，许 钢，李若楠，赵春叶，江娟娟

(安徽工程大学 检测技术与节能装置安徽省重点实验室，安徽 芜湖 241000)

近年来，科学技术迅猛发展，值此方兴未艾之际，计算机视觉技术应运而生，正不断渗透到人们的日常生活中，其中比较重要的内容就是图像中特征点匹配算法的研究，它广泛应用于多个领域中[1-3]，例如移动机器人导航、图像拼接、三维重建以及医学图像分析等计算机视觉领域的基础研究。目前最为广泛的特征点匹配算法有SIFT[4]、SURF[5]、ORB[6]等。

LAWE[4]等人于1999年提出了尺度不变的特征变换SIFT(Scale-invariant Feature Transform)算法，该算法基于特定兴趣点而与图像大小和旋转无关，对于图像旋转、尺度缩放具有较好的稳定性，同时对亮度、视角等条件的微小变化鲁棒性强，但该算法的局部特征点检测和描述子特征是建立在高维的基础上，这使得整个过程计算量庞大、消耗时间多，难以满足实时性的要求。为了克服上述不足，2006年BAY[5]等人基于SIFT的基础上提出一种加速鲁棒性特征SURF(Speeded Up Robust Feature)算法，由于SURF算法最大的特点在于采用了哈尔特征以及积分图像的概念，这使得典型的SURF算子比SIFT算子快大概3倍左右，大大加快了程序执行效率。机器视觉技术的发展使得人们更加关注特征匹配算法在执行效率方面的性能，有大量学者研究表明，ORB算法的运行速度比上述两种算法快至少一个数量级。该算法于2011年由RUBLEE[6]等人在ICCV上提出，它在特征点质量和性能间取得了较好的折中。从实时性角度评测，它是目前运行速度较快的算法。ORB是一种局部不变特征检测子，即图像发生旋转变换时仍可以保持很好的鲁棒性，但对于图像尺度变化较大的图像，传统ORB算法的匹配效果却不理想[7]，由于该算法尺度空间的构建环节不够成熟，当图像尺度发生突变时，图像特征匹配的精度会受影响。文献[8-10]分别通过结合SIFT和SURF检测算子使得改进后的ORB算法拥有尺度不变特性，但实时性和匹配精度难以兼得，可见对ORB的研究仍具有非常大的意义。

本论文提出一种基于非线性尺度空间的ORB特征匹配改进算法，该算法借鉴A-KAZE[11](Accelerated-KAZE)算法思想对ORB进行改进，通过构建非线性尺度空间提取显著特征点，使其对尺度变换的图像具备较强的表现。与此同时，使用PROSAC[12](渐进一致性采样)对匹配点对提纯，进而提高ORB算法的匹配质量，从而达到不失精度的条件下满足实时匹配的目的。

1 传统的ORB算法

ORB算法具有局部不变性，该算法采用以速度著称的加速分割测试特征FAST[6](Feature From Accelerated Segment Test)检测特征点，利用旋转二进制鲁棒基元独立特征BRIEF[6](Binary robust independent elementary feature)算法生成描述符，再以Hamming距离为相似性度量准则比较描述符完成粗匹配。其主要步骤如下：

(1)关键点提取：采用o-FAST算法进行关键点提取，加入Rosin灰度质心法(Intensity Centroid)为其提供方向特性，使得后面的特征描述符具有方向信息；

(2)建立特征描述符：ORB算子采用具备旋转角度的改进BRIEF算法，即rBRIEF算法。其主要思想是依据像素点灰度值的大小，利用随机选点机制在某个特征点的周边选取一定数量的像素点对测试集，生成二进制串描述符；

(3)特征点粗匹配：以Hamming距离作为相似性度量准则对描述子进行比较，若满足一定的条件则认为该特征点匹配对是正确的。该方法原理简单易于操作。

2 改进的ORB特征匹配算法

本文提出的一种基于非线性尺度空间的改进ORB算子，其主要流程如1所示。

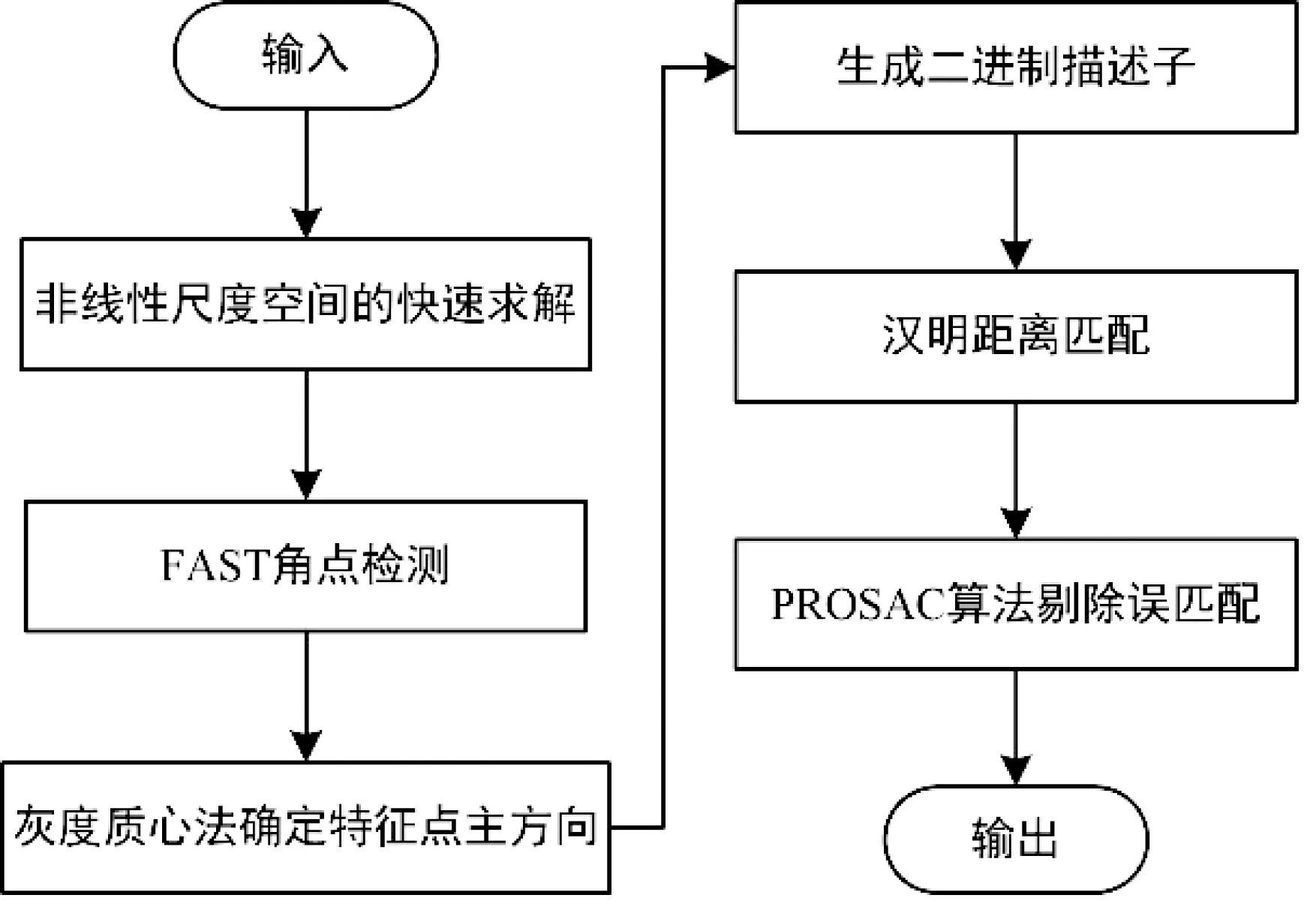
图1 改进ORB算法流程图Fig.1 Improved ORB algorithm flow chart

首先借鉴A-KAZE[8]算法原理利用FED数值分析框架来求解可变传导扩散方程，进而完成非线性尺度空间的构建；其次采用FAST-9算法在非线性尺度空间的每一层进行特征点的检测并计算特征点的质心方向；再次结合之前获取的具有方向特性的特征点，采用rBRIEF算法生成具有二进制字符串特点的特征描述子；最后使用FLANN方法计算汉明距离进行特征点的粗匹配，再对其匹配结果采用PROSAC算法(改进的RANSAC算法)剔除噪声点，实现更加精准的匹配。

2.1 尺度空间的构建

由于传统的ORB算法没有很好的解决尺度不变性，所以在进行角点检测之前要对其构建尺度空间。传统的基于Gaussian尺度空间的构建存在最大的缺陷就是高斯滤波无法保留边缘、边界、细节信息，它会把所有尺度的细节和噪声平滑到相同的水平，这导致其位置精度和独特性大打折扣。而基于A-KAZE算法的非线性尺度分解有望解决上述不足。

2.1.1非线性扩散

鉴于传统的正向欧拉法在求解非线性方程数值时，迭代收敛步长非常短、消耗时间资源很大导致计算复杂度高。针对上述不足，本文在构建一个类似金字塔型的非线性尺度空间来求解非线性滤波扩散方程时，采用快速显示扩散FED[13](Fast explicit diffusion)算法。可以通过非线性偏微分方程来描述传导方程：

(1)

式(1)中，div和L分别为散度与图像L的梯度求解操作，c(x,y,t)为传导扩散函数；L为图像的亮度矩阵；时间t为尺度因子，其值越大代表图像越简单且尺度越大；其中传导方程中引用的函数c依赖于图像局部差分结构形式的张量或标量，使得扩散能够自适应于图像局部特性，公式定义如下：

c(x,y,t)=g(|Lσ(x,y,t)|)

(2)

(3)

(4)

(5)

式(3)～(5)中参数λ为阈值，是控制扩散级别的对比度因子，决定了图像平滑过程中保留边缘信息量的多少，其值与保留的边缘信息量呈负相关。本文的参数λ取值为70%比例的梯度直方图。根据大量实验得知式(4)所表示的扩散系数比较容易计算，所以也很常用。

2.1.2快速显示扩散算法

A-KAZE算法的尺度空间构造与SIFT类似，该算法提出的FED集显式和半隐式理论的优势于一体。此外，采用显式理论分解盒子滤波[14]来近似高斯滤波器,该技术的实现借鉴了积分图像的思想原理，使得计算的复杂度降低，更加便于应用。其本质思想是将图像金字塔分为O个组和S个组内子层，M=O×S是滤波后整个尺度空间包含的图像总量。且在M次循环操作中每次循环皆为一个n次的迭代过程，我们定义第j次的迭代步长为：

(6)

式(6)中τmax为显示求解稳定条件范围内的最大阈值步长。利用FED算子可以将(1)式用矢量化矩阵表示为：

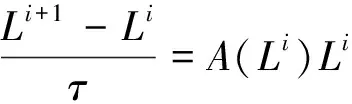
(7)

式(7)中，τ为常量，控制显示扩散的稳定条件；A(Li)为图像亮度在第i层上的传导矩阵，且在整个循环过程中保持不变。

由于非线性偏微分方程不存在解析解，采用FED算法求得(1)式近似解为：

Li+1,j+1=(I+τjA(Li))Li+1,j,j=0,1,…,n-1

(8)

式(8)中，I为单位矩阵，n为显示扩散步数，图像亮度初始化设置为：Li+1,0=Li。

2.1.3非线性尺度空间的构造

采用FED算法来完成尺度空间的创建，该尺度级别按对数递增，与SIFT不同之处是对图像不用进行下采样，它的各个层级均取用与原始图像相同的分辨率。对应的尺度参数σi为：

(9)

由于热传导扩散模型是以时间为单元，故需将以像素为单位的参数σi转化为时间单元。在高斯尺度空间下，使用标准差为σ的高斯核对图像进行卷积，相当于对图像进行持续时间为t=σ2/2的滤波。根据式(9)求出两者的转换公式：进化时间ti。

(10)

最后再结合式(7)求得相应的尺度图像。这样就可以得到一个O组，每组S层的图像金字塔了。

2.2 特征点检测

ORB算法采用改进的FAST算法(oFAST)进行角点检测，早期的Harris和SIFT特征点提取算法都是基于自相关矩阵响应值的算法，一般会涉及到卷积运算，导致运算量庞大，FAST算法刚好克服了这方面的缺陷。ROSTEN等人于文献[15]给出FAST的定义：在某个候选像素点的圆形范围内，通过比较该点与邻域点的灰度差值来判别该点是否为特征点。具体的特征提取过程如下：

(1)确定检测范围：如图2所示，以像素点P为圆心，以3个像素单位为半径画圆，选取圆上16个像素点为待检测的点。

(2)设定合适阈值：将上述(1)中待检测的16个像素点的灰度值与P点灰度值逐一比较，两点灰度值之差的绝对值大于某一阈值εd，则认为这两点是不同的点。特征点的响应函数如下：

(11)

式(11)中I(x)为圆周上任意一个像素点的灰度值，I(p)为圆心像素点的灰度值，对于给定的阈值N0一般取9或12。当N>N0，则认为P为一个角点。重复上述步骤，对除P以外的每一个像素点执行相同的操作，最终找出所有的角点。

(3)增加尺度信息：FAST算子没有提供多尺度特性，这里的改进方法是将上节构建的非线性尺度空间，在其包含的O组，每组S层的图像金字塔上，对每层图像分别进行FAST特征提取，从而形成尺度空间。

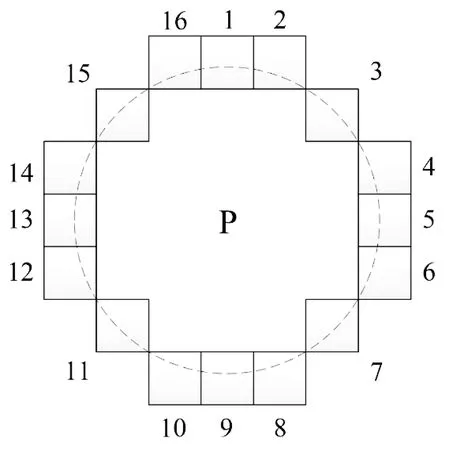
图2 FAST角点检测Fig.2 FAST feature detection

(4)确定图像矩的主方向：ORB采用Rosin灰度质心法使得描述算子具备旋转不变特性。

在一个小的图像块中定义矩为：

(12)

式(12)中，I(x,y)为(x,y)点的灰度表达式。根据式(12)可以得到0阶矩m00和1阶矩m01、m10，通过矩可以找到图像块的质心：

(13)

连接图像块的几何中心O和质心C，得到一个方向向量OC，特征点方向用公式定义为：

(14)

通过以上方法，FAST角点便具备了尺度和旋转的信息。

2.3 特征点描述

ORB算法采用改进的BRIEF算法(rBRIEF)建立描述符，其核心思想是采用随机选点机制在图像中选取像素点，通过比较它们的灰度值从而得到描述符。其具体过程如下：

(1)为消除原BRIEF描述符以像素为测试点所带来的噪声影响，改进算法在特征描述过程中，是以特征点为中心设定邻域为31×31像素的图像块，以此作为测试点集的候选区域。每次测试都是在一个5×5的子窗口内随机选取一个点对(x,y)，使用如下准则进行二进制赋值：

(15)

式(15)中，p(x)为经过高斯平滑后的像素点x=(u,v)T的灰度函数，p(y)同理。

(2)按照一定准则在候选区域内选取n个(xi,yi)点对，即可输出一个由n维二进制字符串表示的描述向量：

(16)

(3)考虑到上述的描述向量没有方向信息，ORB的解决方法是将式(14)的主方向作为特征向量的主方向。对于任意n个待测试点集，引入一个2×n的矩阵Q：

(17)

(4)对矩阵Q进行旋转变换。结合之前通过方向角θ求得相应的旋转矩阵Rθ，就能得到带有方向信息的特征点描述矩阵Qθ：

(18)

(5)得到具有旋转角度的特征描述子：

gn(p,θ)=fn(p)|(xi,yi)∈Qθ

(19)

通过greedy贪婪算法搜索出具有较高方差和较低相关性的n个(文献[6]中n=256)点对作为最终的描述符，大的方差和不相关性有利于描述符保持较大区分性和描述能力的特性，为后续的特征匹配打好基础。

2.4 特征点匹配

上节求得的特征描述符是一个二进制码串，这里先对其采用Hamming距离快速近似最近邻(FLANN)方法进行粗匹配。由于外界噪声因素的影响，粗匹配后的结果仍存在很多伪匹配对，影响匹配效果。故采用PROSAC算法剔除外点，从而提高匹配质量。

其中粗匹配中采用原理简单、操作方便的FLANN算法，该算法在OpenCV库中现已集成。由于RANSAC算法在剔除外点的过程中没有考虑特征点间的差异性，其随机抽样模式会带来迭代次数不稳定、浪费大量计算资源等弊端。本文采用PROSAC算法对特征点粗匹配对进行优化，该方法对包含较多离群点的数据仍然适用。其核心思想是依据一定准则将样本点进行降序排列，在较高匹配率的粗匹配子集中计算模型，从而减少迭代次数，最优估计解也会尽早出现。算法流程如下：

(1)计算粗匹配后的点对集合S中每对匹配点间的距离，根据距离大小对S中的点对进行降序排列；

(2)选取前m个高质量的匹配点对，构成新的样本集S'；

(3)在样本集S'中选取4组质量最高的点对，计算单应矩阵Η；

(5)计算当前内点数量t，若tT，则内点数量更新为t；

(6)内点数量更新为t后，用当前内点集再次计算单应矩阵Η并完成剔除误匹配的工作。

3 实验设置、结果及分析

实验一：针对本文所提出的改进算法，设计了两类实验：(1)尺度不变性对比实验；(2)综合不变性对比实验，即尺度和旋转角度同时改变的情况下进行的实验。使用上述两类实验，分别对两组图像进行测试，其中输入的原始图像格式为.png，像素大小：750×750，两张图像分别取自室内和室外环境。

3.1 尺度不变性测试结果分析

图3 第一组尺度变化下的测试结果图Fig.3 The first set of test results under the scale changes

图4 第二组尺度变化下的测试结果图Fig.4 The second set of test results under the scale changes

通过图3、图4中的(a)、(b)对比实验以及表1不难发现，采用ORB算法的测试效果图中，未提纯前成功匹配的特征点对数目偏少，分别为361、329，提纯后正确匹配的点对数量分别为288、257，其正确匹配率分别为80%和78%。而采用改进算法的测试效果图中，未提纯前成功匹配的特征点对数目较多，分别为428、413，提纯后正确匹配的点对数量分别为398、376，其正确匹配率分别为93%和91%。相较于原算法，改进算法采用快速的FED算子来提高尺度空间的构建速度，并且沿用了ORB特征检测算法。在有效特征点数目增多的情况下，平均匹配精度提升了13%。但由于添加了PROSAC算法二次剔除误匹配点，相较于原ORB算法，运行时间平均增加了21.2 ms。

表1 ORB算法与改进算法的匹配质量比较Tab.1 Comparison of matching quality between ORB algorithm and improved algorithm

3.2 综合不变性测试结果分析

图5 第一组尺度旋转变化下的测试结果图Fig.5 The first set of test results under the change of scale rotation

图6 第二组尺度旋转变化下的测试结果图Fig.6 The second set of test results under the change of scale rotation

图5、图6是针对图像旋转、多尺度的综合测试效果图。表2是针对匹配精度和算法执行时间方面进行的定量分析。结合表2和两组(a)、(b)对比图可以看出，采用原算法的测试效果图中，未提纯前成功匹配的特征点对数量分别为341、314，提纯后正确匹配的点对数目分别为276、236，其准确率分别为81%和75%。而采用改进算法的测试效果图中，未提纯前成功匹配的特征点对数量分别为423、408，提纯后正确匹配的点对数目分别为389、359，其准确率分别为92%和88%。由此可得，改进算法提取到的特征点更加丰富，且增加了二次提纯特征点匹配对的环节，因此在匹配精度上平均提升了12%，在运行时间上平均增加了23.47 ms，但不影响实际应用中算法的实时性。

表2 ORB算法与改进算法的匹配质量比较Tab.2 Comparison of matching quality between ORB algorithm and improved algorithm

实验二：为了进一步验证改进算法的性能，通过复现率[16]来检测在不同尺度下提取特征点的鲁棒性。复现率是指两帧图像上提取到的相同点对数量占总提取点对数的百分比，评测公式如下：

(20)

式(20)中，min(di,dj)为基准图、待匹配图中提取的特征点数目的最小值；Dij为两幅图的重复点数。复现率越高表示特征匹配算法的鲁棒性越强，即该算法越稳定。实验二是对取自室外的图像(柯基图)进行实验，检测不同尺度σ(σ∈[1,3])下的角点，实验结果如下：

图7 不同尺度下复现率比较Fig.7 Comparison of recurrence rates at different scales

由图7不难发现，改进算法相较于原ORB算法，在尺度不变性方面鲁棒性更强，且角点检测更加稳定。

4 结语

本文针对ORB算法没有解决尺度不变性、误匹配率高等问题，提出优化算法。首先通过借鉴A-KAZE算法原理构建非线性尺度空间，其次沿用ORB算子在每层尺度空间的图像上进行特征提取并计算描述子，再次使用FLANN算子和PROSAC算法双重筛选原则剔除误匹配，最终得到匹配质量较高的结果。实验结果表明，改进算法有效地解决了尺度不变性的问题，提取到的特征点在细节和边缘方面处理得更好，并且匹配精确度和算法效率得到了一定改善，适用于匹配精度高、尺度变化较大的应用场景。