Different Types of Solutions for Nonlinear Fractional Integral Boundary Value Problems with Two Parameters
2020-01-10WANGWenxia王文霞MIFang米芳
WANG Wenxia(王文霞),MI Fang(米芳)
(Department of Mathematics,Taiyuan Normal University,Jinzhong 030619,China)
Abstract: This paper is concerned with the existence of different types of solutions for a class of nonlinear fractional differential equations with two parameters in integral boundary conditions.By using a fixed point theorem and analytic technique,we divide the range of these parameters for the existence of positive solutions,negative solutions and sign-changing solutions for the boundary value problem and obtain some new results.
Key words: Fractional integral boundary value problem; Parameter; Positive solution;Negative solution; Sign-changing solution
1.Introduction and Preliminaries
Fractional differential equations,as excellent mathematical models to study various actual problems with memory and hereditary properties,have attracted considerable attention in the last ten years.[1−2,3−7]
Recently,some authors studied fractional integral boundary value problems with disturbance parameters in the boundary conditions,and obtained some interesting results.[8−9]By using the upper and lower solutions method and fixed point index theory.JIA et al.[8]discussed the existence of positive solutions for the following problem with a disturbance parameter

where 1<α ≤2,f ∈C([0,1]×R+,R+),mi,ni ≥0,m2i+n2i >0,i=1,2,k ∈C(R+,R+),µ∈R+.It is interesting to point out that such a disturbance parameterµis always inevitable to exist in applying the differential equation theory to solve the actual problems.In addition,another kind of fractional boundary value problems has also attracted the attention of some researchers.For example,by using fixed point index theory,ZHANG et al.[10]studied the existence of positive solutions for the fractional differential equations

where 3< α ≤4,0< η ≤1 and 0≤<1.By applying a fixed-point theorem in cone and the Leray-Schauder nonlinear alternative,HE[11]investigated the existence of positive solutions for the following integral boundary value problem

WANG et al.[12]applied the Guo-Krasnoselskii fixed point theorem to discuss the existence of positive solutions for the following problem

We observe thatξin the above-mentioned boundary value problems is actually a constant such that the corresponding Green’s function is nonnegative,not a parameter.Indeed,whenξis a parameter,the sign of the corresponding Green’s function will change with the change of the parameter value,which will inevitably affect the properties of solutions for the boundary value problem.So,it is very significant to investigate the impact of such a parameterξon properties of solutions.However,few papers have reported on this topic.
Motivated by[8-12],in this paper we will investigate the fractional boundary value problem (BVP)with two parametersξandµas follows:

whereCDα0+is the Caputo fractional derivative of orderα,1< α <2,f ∈C([0,1]×R,R+),R+=[0,+∞),ξ >0 andµ≥0 .
Letxbe a solution of boundary value problem (1.1),xis called a positive solution ifx(t)≥0 andx(t)0 fort ∈[0,1];xis called a negative solution ifx(t)≤0 andx(t)0 fort ∈[0,1];xis called a non-negative solution(non-positive solution)ifx(t)≥0(x(t)≤0)fort ∈[0,1]; andxis called a sign-changing solution if there existt1,t1∈[0,1]such thatx(t1)x(t2)<0.
The purpose of this paper is to discuss the impact of parametersξandµon the existence of positive solutions,negative solutions and sign-changing solutions for boundary value problem (1.1)by using the nonlinear alternative of Leray-Schauder type (Lemma 1.3)and analytic technique.
The paper is organized as follows.In Section 2,we present Green’s function associated with the boundary value problem (1.1)and discuss some properties of Green’s function.
Moreover,we establish an operator equation equivalent to the boundary value problem (1.1).In Section 3,we divide the range of parametersξandµon the existence of at least one positive solution,one negative solution and one sign-changing solution for the problem (1.1).These results show that the influence of two parametersξandµon the existence of different types of solutions for the boundary value problem.In Section 4,we give two examples to illustrate our main results.
In the rest of this section,we present some basic notations and results.
Definition 1.1[1−2]Letx:(0,+∞)→R be a function andα >0.The Riemann-Liouville fractional integral of orderαofxis defined by

provided that the integral exists.
Definition 1.2[1−2]Letx:(0,+∞)→R be a function andα >0.The Caputo fractional derivative of orderαofxis defined by

provided that the right side is pointwise defined on(0,+∞),wheren=[α]+1,n−1<α wherenis the smallest integer greater than or equal toα. Lemma 1.2[1−2]Letα>0 andx ∈C[0,1],then Lemma 1.3[12]LetEbe a Banach space,Xa convex set ofE,Ωa relatively open subset ofX,andp ∈Ω.Suppose thatT:is a continuous and compact map,then either (i)Thas a fixed point in,or (ii)there existu ∈∂Ωandλ ∈(0,1)such thatu=λTu+(1−λ)p. In this section,we shall present the corresponding Green’s function and its properties;moreover,we present the operator equation which is equivalent to boundary value problem(1.1).This is important for our research. Fory ∈C[0,1],consider the linear fractional boundary value problem whereξ >0 andµ≥0. Lemma 2.1Forξ≠1,BVP(2.1)has a unique solution which is given by where and ProofFrom Lemma 1.1 we get Noticing thatx′(0)=0 andthenc1=0 andµ.This means that Moreover,we have Substituting the value into (2.5)we can obtain that On the other hand,ifxsatisfies (2.2),then Hence,it follows from Lemma 1.2 that(t)=−y(t).Moreover,we easily check thatxis a solution of BVP(2.1).The proof is complete. Lemma 2.2G(t,s)is continuous on [0,1]×[0,1],and monotone decreasing intfor everys ∈[0,1].In addition,the following properties are satisfied: (i)When 0< ξ <1,0≤fort,s ∈[0,1],and (ii)When 1< ξ ≤α,fort,s ∈[0,1],and (iii)Whenξ >α,G(0,0)=and ProofIt follows from (2.3)and (2.4)that Obviously, where It is obvious thatG(t,s)is continuous on[0,1]×[0,1],and monotone decreasing intfor everys ∈[0,1].Next to show properties (i),(ii)and (iii). (i)When 0<ξ <1,the property (i)follows from (2.7). (ii)When 1<ξ ≤α,it is easy to see that This together with (2.7)leads to the property (ii). (iii)Whenξ >α,we haveG(0,0)=Arguing similarly to the property (ii)we can obtain This completes the proof. SetE=C[0,1].The Banach space of all continuous functions on [0,1]with the norm||x||=max {|x(t)| | t ∈[0,1]}.LetP= {x ∈C[0,1]| x(t)≥0,t ∈[0,1]},thenPand−Pare cones inE. Forξ≠1,define the operatorT(ξ,µ)by then,it follows from Lemma 2.2 thatT(ξ,µ):C[0,1]→C[0,1], Moreover,forξ≠1,it is clear by Lemma 2.1 thatxis a solution of BVP(1.1)⇔xis a solution of the operator equationT(ξ,µ)x=xinE. Lemma 2.3The operatorT(ξ,µ):E→Eis completely continuous forξ ∈(0,1)∪(1,+∞)andµ∈[0,+∞). ProofThe proof is similar to that of Lemma 2.2 in [9]. Throughout this paper,we always use the following denotations for a positive constantr. In this section,we give some results on the existence of solutions and non-zero solutions for BVP (1.1).Furthermore,we discuss the impact of parametersξandµon various types of solutions. Lemma 3.1Ifx(ξ,µ)is a solution of BVP(1.1)forξ ∈(0,1)∪(1,+∞)andµ∈[0,+∞),thenx(ξ,µ)(t)is decreasing int ∈[0,1]. ProofIt follows from (2.6)and (2.8)that Moreover, which implies that the solutionx(ξ,µ)(t)is decreasing int ∈[0,1].This ends the proof. The following conditions will be needed: (H1)There exist nonnegative functionsa,b ∈L[0,1]satisfyingand nonnegative nondecreasing functionψ ∈C[0,+∞)satisfyingsuch that (H3)f(t,0)0 on [0,1]. Firstly,we discuss the existence of solutions and the impact of parametersξandµon non-negative solutions,non-positive solutions and possible sign-changing solutions. Theorem 3.1Suppose that(H1)holds.Then BVP(1.1)has at least one solutionx(ξ,µ)forξ ∈(0,1)∪(1,+∞)andµ∈[0,+∞).In particular, (i)x(ξ,µ)is a non-negative solution for (ξ,µ)∈(0,1)×[0,+∞); (ii)x(ξ,µ)is a non-positive solution for (ξ,µ)∈(1,α]×[0,+∞); (iii)x(ξ,µ)is a possible sign-changing solution withx(ξ,µ)(1)≤0 for (ξ,µ)∈(α,+∞)×[0,+∞). ProofLetξ ∈(0,1)∪(1,+∞)andµ∈[0,+∞)be given.It follows from Lemma 2.2 that Set Suppose,in the contrary,that there existx0∈∂ΩRandλ0∈(0,1)such that that is, Then, This implies that which contradicts(3.1).Therefore,applying Lemma 1.3 we obtain that BVP(1.1)has at least one solutionx(ξ,µ)in,and conclusions (i)and (ii)follow from (2.9).Note that This,together with(2.8)and Lemma 3.1,leads to the conclusion(iii).The proof is complete. Theorem 3.2Suppose that(H2)holds.Then BVP(1.1)has at least one solutionx(ξ,µ)forξ ∈(0,1)∪(1,+∞)andµ∈[0,+∞).In particular, (i)x(ξ,µ)is a non-negative solution for (ξ,µ)∈(0,1)×[0,+∞); (ii)x(ξ,µ)is a non-positive solution for (ξ,µ)∈(1,α]×[0,+∞); (iii)x(ξ,µ)is a possible sign-changing solution withx(ξ,µ)(1)≤0 for (ξ,µ)∈(α,+∞)×[0,+∞). ProofWe prove all statements by three steps. (i)Let (ξ,µ)∈(0,1)×[0,+∞)be given.According to (2.9),we only need to find a fixed point ofT(ξ,µ)inP.From (H2)there existsl1>0 such that We assert that there existsR1>0 such that In order to prove the assert we consider two cases. Case 1fis bounded on [0,1]×[0,+∞),that is,there existsM1>0 such thatf(t,x)≤M1for (t,x)∈[0,1]×[0,+∞).TakeR1>thenwhich meansSuppose,in the contrary,that there existx1∈P ∩∂ΩR1andλ1∈(0,1)such that that is, Moreover, which impliesR1 Case 2fis unbounded on[0,1]×[0,+∞).In this case,we takesuch that that is, This,together with (3.3)and (3.4),gives which implies a contradictionR1 (ii)Let (ξ,µ)∈(1,α]×[0,+∞)be given.From (2.9)we only need to find a fixed point ofT(ξ,µ)in−P.It follows from (H2)that there existsl2>0 such that By similar argument as the above (i),we can takeR2as follows:If there existsM2>0 such thatf(t,x)≤M2for (t,x)∈[0,1]×(−∞,0],we takeIffis unbounded on [0,1]×(−∞,0],we takesuch that (iii)Let (ξ,µ)∈(α,+∞)×[0,+∞)be given.Similarly,there existsl3>0 such that By similar argument as the above (i),we can takeR3as follows:If there existsM3>0 such thatf(t,x)≤M3for (t,x)∈[0,1]×(−∞,+∞),we takeR3>Iff(t,x)is unbounded on [0,1]×(−∞,+∞),we takesuch that In the sequence,we discuss the existence of non-zero solutions and the impact of parametersξandµon positive solutions,negative solutions and sign-changing solutions. For the convenience,for givenx ∈C[0,1]we set whereI=(α,+∞)×[0,+∞)andI0=(α,+∞)×(0,+∞). Lemma 3.2Suppose that (H3)holds.Ifx(ξ,µ)is a solution of BVP(1.1)forξ ∈(0,1)∪(1,+∞)andµ ∈[0,+∞),thenx(ξ,µ)(t)0 on [0,1],and satisfies the following properties: (i)x(ξ,µ)is a positive solution for (ξ,µ)∈(0,1)×[0,+∞); (ii)x(ξ,µ)is a negative solution for (ξ,µ)∈(1,α]×[0,+∞); (iii)x(ξ,µ)is a sign-changing solution and negative solution for (ξ,µ)∈Λ(x(ξ,µ))and(ξ,µ)∈IΛ(x(ξ,µ)),respectively. ProofSuppose,in the contrary,thatx(ξ,µ)(t)≡0 on [0,1],then which implies that SinceG(0,s)−G(1,s)=(1−s)α−1fors ∈[0,1], This implies thatf(t,0)≡0 on [0,1],which contradicts (H3).Therefore,x(ξ,µ)is a non-zero solution of BVP(1.1).This,together with (2.9),leads to properties (i)and (ii). Next to show property (iii).For (ξ,µ)∈(α,+∞)×[0,+∞)=I,there are two cases to be considered. Case 1 (ξ,µ)∈Λ(x(ξ,µ)).Noting that then which implies thatx(ξ,µ)(0)>0.In addition,it follows from (3.2)thatx(ξ,µ)(1)<0.Thus,we obtain thatx(ξ,µ)is a sign-changing solution. Case 2 (ξ,µ)∈IΛ(x(ξ,µ)).From (3.5),we havex(ξ,µ)(0)≤0,which together with Lemma 3.1 yields thatx(ξ,µ)(s)≤0 fort ∈[0,1].Sincex(ξ,µ)(t)0 on [0,1],x(ξ,µ)is a negative solution.The proof is complete. Lemma 3.3Ifx(ξ,µ)is a solution of BVP(1.1)forξ ∈(0,1)∪(1,+∞)andµ∈(0,+∞),thenx(ξ,µ)(t)0 on [0,1],and satisfies the following properties: (i)x(ξ,µ)is a positive solution for (ξ,µ)∈(0,1)×(0,+∞); (ii)x(ξ,µ)is a negative solution for (ξ,µ)∈(1,α]×(0,+∞); (iii)x(ξ,µ)is a sign-changing solution and a negative solution for (ξ,µ)∈Λ0(x(ξ,µ))and(ξ,µ)∈I0Λ0(x(ξ,µ)),respectively. ProofIn order to show thatx(ξ,µ)(t)0 on [0,1],We consider two cases off(t,0). Iff(t,0)0 on [0,1],then the condition (H3)holds.It follows from Lemma 3.2 thatx(ξ,µ)(t)0 on [0,1]. Iff(t,0)0 on [0,1],then it follows from (2.8)andµ >0 thatx(ξ,µ)(t)0 for anyt ∈[0,1]. In addition,arguing similarly to Lemma 3.2,we can finish proofs of properties (i),(ii)and (iii).Thus,the proof is complete. According to Theorem 3.1,3.2 and Lemma 3.2,we can obtain the following result. Theorem 3.3Suppose that (H1)and (H3)hold.Then BVP(1.1)has at least one non-zero solutionx(ξ,µ)forξ ∈(0,1)∪(1,+∞)andµ∈[0,+∞).Furthermore, (i)x(ξ,µ)is a positive solution for (ξ,µ)∈(0,1)×[0,+∞); (ii)x(ξ,µ)is a negative solution for (ξ,µ)∈(1,α]×[0,+∞); (iii)x(ξ,µ)is a sign-changing solution and a negative solution for (ξ,µ)∈Λ(x(ξ,µ))and(ξ,µ)∈IΛ(x(ξ,µ)),respectively. Theorem 3.4Suppose that (H2)and (H3)hold.Then BVP(1.1)has at least one non-zero solutionx(ξ,µ)forξ ∈(0,1)∪(1,+∞)andµ∈[0,+∞).Furthermore, (i)x(ξ,µ)is a positive solution for (ξ,µ)∈(0,1)×[0,+∞); (ii)x(ξ,µ)is a negative solution for (ξ,µ)∈(1,α]×[0,+∞); (iii)x(ξ,µ)is a sign-changing solution and a negative solution for (ξ,µ)∈Λ(x(ξ,µ))and(ξ,µ)∈IΛ(x(ξ,µ)),respectively. In virtue of Theorems 3.1,3.2 and Lemma 3.3,we can obtain the following results. Theorem 3.5Suppose that (H1)holds.Then BVP(1.1)has at least one non-zero solutionx(ξ,µ)forξ ∈(0,1)∪(1,+∞)andµ∈(0,+∞).Furthermore, (i)x(ξ,µ)is a positive solution for (ξ,µ)∈(0,1)×(0,+∞); (ii)x(ξ,µ)is a negative solution for (ξ,µ)∈(1,α]×(0,+∞); (iii)x(ξ,µ)is a sign-changing solution and a negative solution for (ξ,µ)∈Λ0(x(ξ,µ))and(ξ,µ)∈I0Λ0(x(ξ,µ)),respectively. Theorem 3.6Suppose that (H2)holds.Then BVP(1.1)has at least one non-zero solutionx(ξ,µ)forξ ∈(0,1)∪(1,+∞)andµ∈(0,+∞).Furthermore, (i)x(ξ,µ)is a positive solution for (ξ,µ)∈(0,1)×(0,+∞); (ii)x(ξ,µ)is a negative solution for (ξ,µ)∈(1,α]×(0,+∞); (iii)x(ξ,µ)is a sign-changing solution and a negative solution for (ξ,µ)∈Λ0(x(ξ,µ))and(ξ,µ)∈I0Λ0(x(ξ,µ)),respectively. To illustrate how our main results can be used in practice we present some examples. Example 4.1In BVP(1.1),let 1<α<2 andf(t,x)=etg(x)+te−tfort ∈[0,1]andx ∈(−∞,+∞),where Then (H2)and (H3)are satisfied.Therefore,applying Theorem 3.4 we obtain that BVP(1.1)has at least one non-zero solutionx(ξ,µ)forξ ∈(0,1)∪(1,+∞)andµ∈[0,+∞),furthermore,x(ξ,µ)is a positive solution,a negative solution,and a sign-changing solution for (ξ,µ)∈(0,1)×[0,+∞),(ξ,µ)∈((1,α]×[0,+∞))∪(IΛ(x(ξ,µ))),and(ξ,µ)∈Λ(x(ξ,µ)),respectively. Example 4.2In BVP(1.1),let 1< α <2 andf(t,x)=φ(t)|x|qfort ∈[0,1]andx ∈(−∞,+∞),where 0≤q <1 andφ ∈C[0,1]withφ(t)≥0 andφ(t)≡0 fort ∈[0,1].It is easy to check that (H2)is satisfied.Applying Theorem 3.6 we obtain that BVP(1.1)has at least one non-zero solutionx(ξ,µ)forξ ∈(0,1)∪(1,+∞)andµ∈(0,+∞),furthermore,x(ξ,µ)is a positive solution,a negative solution and a sign-changing solution for(ξ,µ)∈(0,1)×(0,+∞),(ξ,µ)∈((1,α]×(0,+∞))∪(I0Λ0(x(ξ,µ)))and (ξ,µ)∈Λ0(x(ξ,µ)),respectively.
2.Equivalent Operator Equation


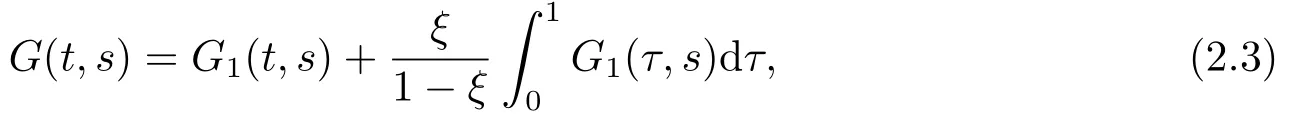















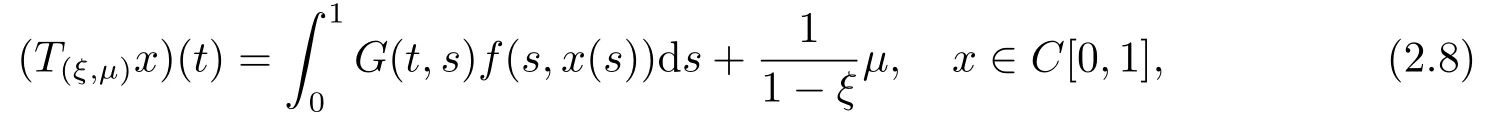


3.Existence of Various Types of Solutions















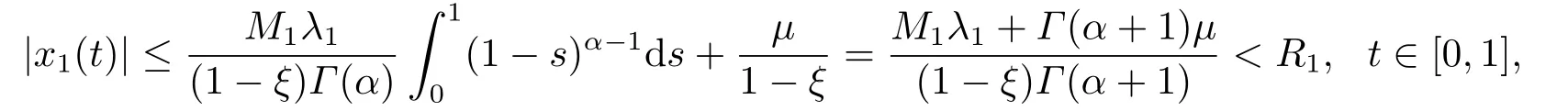


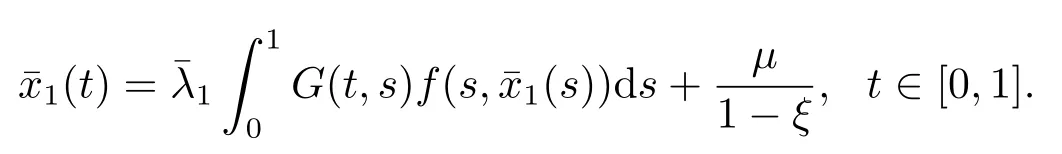











4.Examples

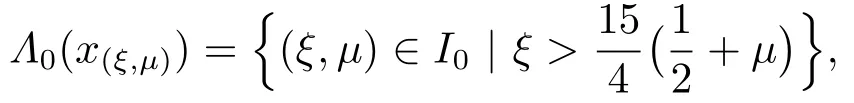

杂志排行
应用数学的其它文章
- Threshold Dynamics of Discrete HIV Virus Model with Therapy
- Solvability for Fractional p-Laplacian Differential Equation with Integral Boundary Conditions at Resonance on Infinite Interval
- Long-Time Dynamics of Solutions for a Class of Coupling Beam Equations with Nonlinear Boundary Conditions
- Existence and Uniqueness of Mild Solutions for Nonlinear Fractional Integro-Differential Evolution Equations
- 基于Markov链的税延型养老保险跨期效用
- 动态投资组合现金次可加风险度量的时间相容性
