基于增广Lagrange函数的约束优化问题的一个信赖域方法

柳颜,贺素香

(武汉理工大学理学院,湖北 武汉430070)

1.引言

不等式约束优化问题是一类传统的优化问题,其广泛应用于经济学、工程学、运输科学、数学规划等诸多领域,因此对其理论及方法的研究也具有重要的意义.本文主要研究下述形式的不等式约束优化问题:

其中x ∈Rn,f(x):Rn→R,ci(x):Rn→R都是二阶连续可微函数.

目前已有许多解决不等式约束优化问题(1.1)的方法,如拉格朗日-牛顿法、罚函数法、可行方向法、逐步二次规划方法、有效集法、增广Lagrange方法、信赖域法等[1−3].其中罚函数法是过去几十年发展起来的一种解决约束优化问题的重要方法.罚函数方法的重要思想是通过添加罚因子,在目标函数上加上由约束函数组成的一个惩罚项,来迫使迭代点逼近可行域,从而将约束优化问题转化为无约束优化问题.常用的罚函数是不带有乘子的罚函数和l∞罚函数及带有乘子的增广Lagrange函数,而l1罚函数和l∞罚函数是非光滑的,可能会导致Maratos效应[4],而且其子问题也是非光滑的,导致该子问题不容易解决.基于Bertsekas[5]构造的指数型增广Lagrange函数光滑性的优点,本文将应用该函数来研究问题(1.1)的求解方法.

增广Lagrange方法是解决问题(1.1)的重要方法之一.在传统的增广Lagrange方法的第二步中,即在第k次迭代时,通过精确求解以增广Lagrange函数为目标函数的无约束子问题以获得问题(1.1)的解,但是精确求解该子问题时所需的计算工作量比较大.在文[6]中Conn提出一类方法来解决以增广Lagrange函数为目标函数的无约束子问题,其中他们考虑了该子问题的一阶临界条件满足给定的一个精度范围内,并且当该精度收敛到0时,由这种方法产生的序列点收敛到KKT点或者Fritz-John 点.但是,在实际问题中,当目标函数可能高度非线性和精度非常小时,这会造成相应程序非常复杂,计算代价会很大.

信赖域方法是从Levenberg(1944)和Marguart(1963)解决无约束优化问题的工作开始的,之后许多学者对这类方法有了更深入的研究.Fletcher[7]和Powell[8]等人的工作表明了很好的收敛性和有效的计算性是信赖域方法的主要特性.目前信赖域方法的研究在等式约束优化问题[9−11]和线性不等式约束优化问题[12−13]中都有重要进展.WANG和YUAN14]针对等式约束优化问题提出了一个增广Lagrange信赖域方法.该方法考虑在每步迭代中只需要在相应信赖域中极小化经典增广Lagrange函数的二次近似,从而使得计算子问题的难度降低,并且通过对信赖域子问题的求解得到等式约束优化问题的近似解.鉴于目前还没有学者采用上述方法思想研究不等式约束优化问题,基于Bertsekas[5]构造的指数型增广Lagrange函数,本文将用信赖域方法去解决以指数型增广Lagrange函数为目标函数的无约束子问题,并建立相应的信赖域算法.在一定的假设条件下,本文将证明算法的全局收敛性,并最后给出相应经典算例的数值实验结果以验证算法的有效性.

2.基础知识

定义2.1设问题(1.1)的可行域为F,并在后文中假设F是非空集.对x ∈F,定义在可行点x处的紧约束的指标集I(x)为:

定义2.2定义问题(1.1)的Lagrange函数为L(x,λ)=f(x)−其中λ=(λ1...λm)T为Lagrange乘子.

定理2.1[15](KKT条件)设x∗是问题(1.1)的局部极小点,f(x),ci(x)(x ∈D)在x∗点处可微.若向量组 {∇ci(x∗)(i ∈Ix∗))}线性无关,则存在向量λ∗=(λ1∗...λm∗)T使得下式成立

此时称(x∗,λ∗)为问题(1.1)的KKT解对,并且称x∗为问题(1.1)的KKT点.

记ci−(x)=min {ci(x),0}(i ∈D),则问题(1.1)中ci(x)≥0等价于ci−(x)=0,记c−(x)=(c1−(x),...,cm−(x))T.

3.一种信赖域方法

本文将主要用到Bertsekas[5]构造的基于不等式约束优化问题的指数型增广Lagrange函数,其形式如下:

其中λ是Lagrange乘子,σ >0是罚因子.在传统的增广Lagrange方法的第二步中,求解如下子问题：

为了减少精确求解该子问题的计算量,本文将采用信赖域方法解决该子问题.

在第k次迭代时定义增广Lagrange函数(3.1)的二次近似函数：

其中∆k是信赖域半径.

记dk是问题(3.3)的解.为了判别dk能否被接受,定义如下比值

其中Aredk是问题(3.2)中目标函数(3.1)的真实下降量,Predk是问题(3.2)中目标函数(3.1)的预估下降量.

下面给出基于增广Lagrange函数(3.1)的求解问题(1.1)的信赖域算法.

算法3.1步0 给定初始点x0∈Rn,λ0∈Rm,σ0>0,∆0>0,δ0>0,ε ≥0,k:=0.

步2 求解子问题(3.3),得到dk;

步3 按式(3.4)计算ρk.若ρk >η,则xk+1=xk+dk,转步4;

否则xk+1=xk,∆k+1=/4,k=k+1,转步2.

步4 更新Lagrange乘子和罚因子：

如果Predk <δkσkmin {∆k,},则σk+1=2σkδk+1=δk/4；

否则σk+1=σkδk+1=δk.

步5 更新信赖域半径：

更新矩阵Bk得到Bk+1；k:=k+1,转步1.

4.收敛性分析

本节首先对问题(1.1)作出一些假设条件,然后在这些假设条件下,证明算法3.1的全局收敛性.

设 {xk},{Bk}是由算法3.1产生的序列,下面给出证明中需要用到的一些假设条件:

(A1)f(x),ci(x)i ∈D是二阶连续可微函数;

(A2)序列 {xk},{Bk}是有界的.

引理4.1假设(A1)成立,则∇x(xk+1,λk,σk)=∇xL(xk+1,λk+1).

证由(3.1)和(3.5)计算得

引理4.2记Hk=∇x(xk,λk,σk).设dk是问题(3.3)解,并且则有

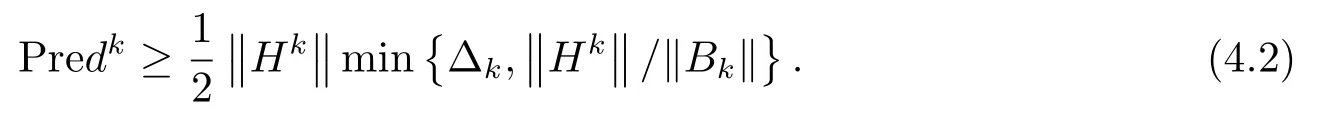
证定义其中α ∈[0,1].由于则是问题(3.3)的可行点.

从而有

故结合(4.3)式可知(4.2)式成立.

即引理4.2得证.

定理4.3假设(A1)-(A2)成立,则

证首先证明

假设(4.4)式不成立,则对任意的k,存在一个正常数v使得

如果对充分大的k有σk=σ,则由算法3.1中的步4可知对充分大的有

然而对于充分大的k,由假设条件(A2),即 {Bk}是有界的,则存在常数N >0,使得||Bk||≤N.由(3.4)式可得

即当k→∞时,ρk→1.此时由算法3.1的步5有∆k+1≥∆k,这与∆k→0矛盾.故(4.4)式成立.

记U是所有成功迭代对应的指标所构成的集合.下面证明||c−(xk)||收敛到0.用反证法.假设存在指标集mj ⊂U及常数τ >0使得

其中c−i是由c−i(xk)(i ∈mj)组成的列向量.

由(4.4)式可知,存在子列nj ⊂U使得

对于mj ≤u ≤nj,由引理4.2可知

可知Aredk是有下界的.

对充分大的k,有

其中ζ为一正数.由Aredk的有界性,因此

0(k→∞).

基于(4.6)式,对充分大的u,都有有这与(4.5)式相矛盾,因此定理得证.

定理4.4假设(A1)-(A2)成立,dk设是问题(3.3)解,并设是序列 {xk}的聚点.如果向量组线性无关且满足互补松弛条件,则x是问题(1)的KKT点.

证首先需要证明记即证0.

由(3.4)可知

即 {L(xk,λk,σk)}单调下降且下有界,从而

由算法3.1的步3和引理4.2可知

当k→∞时,则根据(4.7)式可知∆k→0.从另一个方面可得

以及

从而可得

因此有

根据(4.8)式表明:当时k→∞,有∆k+1≥∆k,这与∆k→0矛盾.故有

假设对所有的k,λk是有界的,由定理4.3,则序列 {xk}存在一个聚点和 {λk}存在一个聚点,使得向量组∇ci()(i ∈I)线性无关且聚点x满足互补松弛条件,由引理4.1可得,

即定理4.4得证.

5.数值实验

下面利用算法3.1和传统的增广Lagrange算法[15]分别对附录中的不等式约束优化问题进行实验,并对数值实验结果进行分析.

测试环境：所有实验均在联想R720笔记本电脑上运行,操作系统为Windows10,处理器为Intel酷睿四核处理器,2.5GHz,8G内存.本文的程序代码都是用Matlab语言编写的,并在Matlab R2016a平台上运行.

初始值的选取：两种算法中的初始点,初始Lagrange乘子都是相同的.算法3.1中用到的部分参数定义如下：

实验结果中用n表示附录问题中的变量个数,m表示附录问题中的约束函数个数,k表示迭代次数.表5.1列出了两种算法处理不同维度的不等式约束优化问题的实验结果.

表5.1 算法3.1和传统的增广Lagrange算法的数值比较结果

由表5.1可以看出,对于不同维度的测试问题,算法3.1在迭代次数和迭代时间上均少于传统的增广Lagrange算法,这说明本文提出的基于信赖域方法思想的算法减少了求解问题(1.1)的计算量; 同时表5.1给出的数值实验结果验证了算法3.1的有效性.

附录

问题1[15]

最优解和最优值：x∗=(1,0)T,f(x∗)=0.

初始点和初始Lagrange乘子：x0=(0,0)T,λ0=(1,1)T.

问题2Beale问题[16]

最优解和最优值：x∗=(4/3,7/9,4/9)T,f(x∗)=1/9.

初始点和初始Lagrange乘子：x0=(0,0,0)T,λ0=(1,1,1)T

问题3Rosen-Suzuki问题[16]

最优解和最优值：x∗=(0,1,2,−1)T,f(x∗)=−44.

初始点和初始Lagrange乘子：x0=(2,2,2,2)T,λ0=(1,1,1,1)T.

问题4Wong问题(1)[16]

最优解和最优值：x∗=(2.3305,1.9514,−0.4775,44.3657,−0.62449,1.0381,1.5942)T,f(x∗)=680.630

初始点和初始Lagrange乘子：x0=(1,2,0,4011)T,λ0=(1,1,1,1)T.