Existence of Positive Solutions for a Kind of Nonlinear Fractional Differential Equation with Nonlinear Boundary Value Conditions
2020-01-10LIMengting李梦婷ZHANGKemei张克梅
LI Mengting(李梦婷),ZHANG Kemei(张克梅)
(School of Mathematical Sciences,Qufu Normal University,Qufu 273165,China)
Abstract: In this paper,we use mixed monotone operator method to deal with the existence and uniqueness of positive solutions to a kind of boundary value problem of the nonlinear fractional order differential equation.Our analysis is based on one new fixed point theorem for the mixed monotone operator.As an application,we also give a simple example to prove our main conclusions.
Key words: Positive solution; Mixed monotone operator; Riemann-Liouville fractional derivative; Existence and uniqueness
1.Introduction
In this paper,we investigate the existence and uniqueness of positive solution for the fractional boundary value problem(BVP for short)of the form:

where 3< α ≤4,β >1,is the Riemann-Liouville fractional derivative,is the Riemann-Liouville fractional integral,f:[0,1]×[0,∞)×[0,∞)→[0,∞),g:[0,∞)→(−∞,0]are continuous functions.
Recently,the theory of boundary value problems has significant application in many areas,and many conclusions were obtained dealing with the existence and uniqueness of solution for the boundary value problems[1−10].
In[1],the authors considered the following fourth-order two point problem with nonlinear boundary conditions:

wheref,gare functions given,the results are given by using the Monotone iterative operator method.
In[5],the authors studied the following fourth-order two point boundary value problem:

wheref ∈C([0,1]×[0,∞)×(−∞,0],[0,∞)).By using the Krasnoselskii fixed point theorem,the author obtained the existence results of at least one positive solution.
Inspired by the work of the above mentioned papers,the aim of this paper is to establish the existence and uniqueness of positive solutions of the BVP (1.1).
To prove our conclusions,we put forward some related definitions and lemmas in Section 2,and we provide some new properties of the Green function that we compute.In Section 3,by using a mixed monotone operator method,the results for the existence and uniqueness of positive solutions of BVP (1.1)are built.To explain our results,we give a simple example in Section 4.
2.Preliminaries and Correlative Lemmas
We first give some essential definitions and lemmas that are significant for the paper.
Definition 2.1[11]The Riemann-Liouville fractional integral of orderα>0 of a functionu:R+→R is given by

whereΓ(α)is the Euler gamma function defined by

Definition 2.2[11]The Riemann-Liouville fractional derivative of orderα >0 of a functionu:R+→R is given by

wheren=[α]+1,provided the right side is pointwise defined on R+.
Remark 2.1[12]In this way,we need the following conclusions:
Lemma 2.1[11]Ifu ∈L1(0,1),α>β >0,then


Lemma 2.2[11]Ifu ∈C(R+)and1(R+),then

whereci ∈R,i=1,2,...,n,n=[α]+1.
Definition 2.3[13]Let(E,||·||)be a real Banach Space.A nonempty,closed and convex setP ⊂Eis a cone if the following two conditions are satisfied:
1)Ifx ∈Pandµ≥0,thenµx ∈P;
2)Ifx ∈Pand−x ∈P,thenx=θ.
Every coneP ⊂Einduces a partial order inEgiven byx1≤x2if and only ifx2−x1∈P.
Definition 2.4[13]If there exists a constantC >0 such that,for anyx,y ∈E,0≤x ≤yimplies||x||≤C||y||,then the conePis said to be normal.In this case,the smallest constantCsatisfying the last inequality is called the normality constant ofP.
Definition 2.5[13]Forx,y ∈E,we denotex∼ywhen there exist constantsλ,µ >0 such thatλy ≤x ≤µy.Clearly∼is an equivalence relation.
Definition 2.6[13]Forh >0,we definePh={x ∈E:x∼h}.It is easily seen thatPh ⊂P.
Definition 2.7[13]An operatorT:E→Eis said to be increasing,if,for anyx,y ∈E,x ≤yimpliesTx ≤Ty.
Definition 2.8[13]An operatorA:P ×P→Pis called mixed monotone,ifA(x,y)is increasing inxand decreasing iny.Hence,for any (x,y),(u,v)∈P ×P,x ≤uandy ≥v ⇒A(x,y)≤A(u,v).
Definition 2.9An operatorB:P→Pis called sub-homogeneous ifB(tx)≥tBx,for anyt ∈(0,1)andx ∈P.
Lemma 2.3Leth ∈C[0,1],3<α ≤4.The unique solution of the following boundary value problem:

can be expressed by
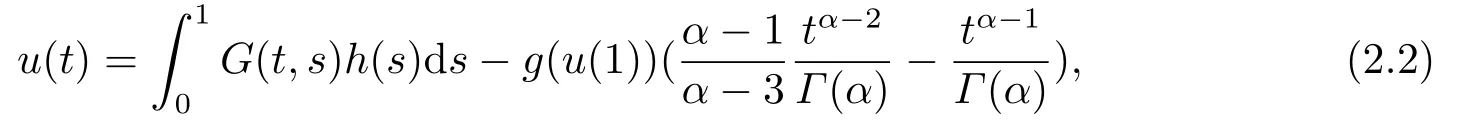
where

ProofBy Lemma 2.2,the solution of (2.1)can be written as

Fromu(0)=u′(0)=0,we know thatc3=c4=0,hence



By the b oundary conditionsu′′(1)=0 and(1)=g(u(1)),we can get
then

So

whereG(t,s)are defined by (2.3).The proof is completed.
Lemma 2.4The functionG(t,s)defined by (2.3)satisfies
1)G(t,s)≥0 is continuous for allt,s ∈[0,1];
2)G(t,s)≥wherey1(s)=1−(1−s)α−3−(α−3)s,for allt,s ∈[0,1];
3)G(t,s)≤wherey2(s)=1−(1−s)α−3,for allt,s ∈[0,1].
Proof1)From (2.3),it is easy to see thatG(t,s)is continuous on [0,1]×[0,1],and obviouslyG(t,s)≥0;
2)When 0≤s ≤t ≤1,
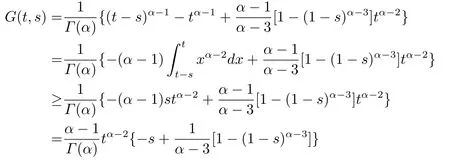
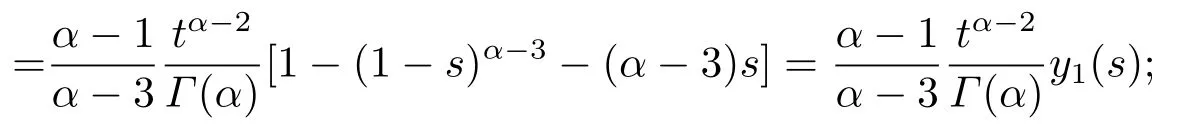
When 0≤t ≤s ≤1,
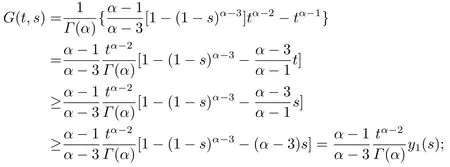
3)When 0≤s ≤t ≤1,

When 0≤t ≤s ≤1,

The proof is completed.
Lemma 2.5[14]Suppose thatγ ∈(0,1),h ∈E,θE for anyλ ∈(0,1)andu,v ∈P.LetB:P→Pbe an increasing sub-homogeneous operator.Assume that (i)there existsh0∈Phsuch thatA(h0,h0)∈PhandBh0∈Ph; (ii)there exists a constantδ0>0 such thatA(u,v)≥δ0Bu,for anyu,v ∈P.Then (a)A:Ph×Ph→PhandB:Ph→Ph; (b)There existsu0,v0∈Phandr ∈(0,1)such thatrv0≤u0≤v0and (c)There exists a uniquex∗∈Phsuch thatx∗=A(x∗,x∗)+Bx∗; (d)For any initial valuesx0,y0∈Ph,the sequences defined by Lemma 2.6[15]The following operator equations whereA:P×P→Pis a mixed monotone operator and the following conditions are satisfied: (A1)There existsh ∈Pwithh≠θsuch thatA(h,h)∈Ph; (A2)For anyu,v ∈Pandt ∈(0,1),there existsφ(t)∈(t,1)such that (A3)Pbe a normal cone ofC[0,1]. Then operator equationA(x,x)=xhas a unique positive solutionx∗inPh.Moreover,for any initial valuesx0,y0∈Ph,the sequences satisfy||xn−x∗||→0 and||yn−x∗||→0 asn→∞. Lemma 2.7[15]Suppose the above (A1),(A2)and (A3)are satisfied,andxλ(λ>0)is the unique solution of parameter equationA(x,x)=λxinPh.Then the following conclusions hold: (B1)Ifφ(t)fort ∈(0,1),thenxλis strictly decreasing inλ,that is,0< λ1< λ2impliesxλ1>xλ2; (B2)If there existsη ∈(0,1)such thatφ(t)≥tηfort ∈(0,1),thenxλis continuous inλ,that is,λ→λ0(λ0>0)implies||xλ−xλ0||→0; In this paper,we consider the spaceE=C[0,1]with the standard norm defined by,forx ∈C[0,1],||x||=max {|x(t)|:t ∈[0,1]}.InC[0,1],we consider the conePdefined by,P= {x ∈C[0,1]:x(t)≥0,t ∈[0,1]}. We give the following conditions: (H1)f(t,x,y)=φ(t,x,y)+ψ(t,x,y),whereφ,ψ:[0,1]×[0,∞)×[0,∞)→[0,∞)are continuous; (H2)For the fixedt ∈[0,1],φ(t,x,y)is nondecreasing inx,y,ψ(t,x,y)is nonincreasing inx,y,andφ(t,0,0)0; (H3)There exists a constantσ ∈(0,1)such that,forx,y ≥0,and for anyt ∈[0,1]andλ ∈(0,1),we have (H4)g:[0,∞)→(−∞,0)is decreasing continuous function andg(κx)≤κg(x),for anyκ ∈(0,1)andx ∈[0,∞); Theorem 3.1Assume that (H1)-(H5)hold.Then 1)BVP (1.1)has a unique positive solutionx∗∈Ph; 2)For anyx0,y0∈Ph,there exist iteration sequencesxn(t),yn(t),forn=1,2,...,such that||xn−x∗||→0 and||yn−x∗||→0 asn→∞,whereh(t)=tα−2,t ∈[0,1]. ProofFirstly,from Lemma 2.3,BVP (1.1)has the following integral formulation: wheret ∈[0,1],G(t,s)is Green’s function appearing in Lemma 2.3. Now,we consider the operators defined by: fort ∈[0,1]andu,v ∈P. From (H1),(H2),we can infer thatA:P ×P→PandB:P→P. Hence,usatisfies the equation (3.1)if and only ifu=A(u,u)+Bu.In the sequel,we check that operatorsA,Bsatisfy all the assumptions of Theorem 2.1. Step 1 It is clear thatPis a normal cone inC[0,1]and the normality constant is 1. Step 2 We explain thatAis a mixed monotone operator.In fact,foru1,u2,v ∈P,withu1≤u2,andt ∈[0,1],from (H2),we have Similarly,foru,v1,v2∈P,v1≤v2,we can get That is,Ais a mixed monotone operator. Step 3 We will prove that forγ ∈(0,1),anyλ ∈(0,1)andu,v ∈P,we have From (H3),there existσ1,σ2∈(0,1)such that Hence,forλ ∈(0,1)andu,v ∈P,we have whereγ=max {σ1,σ2}. Step 4 We are going to prove thatBis an increasing operator.Foru,v ∈P,withu ≤v,sincegis decreasing (the assumption (H4)),g(u(1))≥g(v(1)).Fort ∈[0,1], and this proves thatBis an increasing operator. Step 5 In order to prove thatBis a sub-homogeneous operator,we takeκ ∈(0,1),u ∈Pandt ∈[0,1],from the assumption (H4),we have Therefore,Bis a sub-homogeneous operator. Step 6 We will prove that assumption (i)of Lemma 2.5 holds. Now,we consider the functionh(t)=tα−2,for anyt ∈[0,1].Hence,0≤h(t)≤1,for anyt ∈[0,1]. Before continuing the proof,fort ∈[0,1],we notice So,from (H2),we can get On the other hand, where we have used the assumption (H2)and Lemma 2.4. Put Then,we have Next,we will prove thata1,a2>0.In fact,it is sufficient to prove thata1>0.By the assumption (H2), Hence,A(h,h)∈Ph.Now,we are going to prove thatBh ∈Ph.Fort ∈[0,1],fromg(1)<0,we have On the other hand, Put Then, By (H4),sinceg(1)<0,0 Therefore,Bh ∈Ph. Step 7 In order to prove assumption (ii)of Lemma 2.5,for anyu,v ∈P,by Lemma 2.4 and the assumption (H5),we have This proves that,foru,v ∈P,A(u,v)≥δ0Bu,withδ0=1. Finally,let’s apply Lemma 2.5.There exists a uniquex∗∈Phsuch thatx∗=A(x∗,x∗)+Bx∗.Hence,BVP (1.1)has a unique solutionx∗∈Ph. Moreover,for any initial valuesx0,y0∈Ph,the sequences are defined by forn=1,2,...Whenn→∞,we have||xn−x∗||→0,||yn−x∗||→0. The proof is finished. Remark 3.1If we change the range ofgin the assumption (H4)intog:[0,∞)→(−∞,0],and add the conditiong(1)<0 to Theorem 3.1,then the conclusions still hold. Corollary 3.1Assume that (H1),(H2),(H3)hold.Then the following fractional boundary value problem has a unique positive solutionx∗inPh.Moreover,for any initial valuesx0,y0∈Ph,the sequences ProofFrom (3.2),forγ ∈(0,1),anyλ ∈(0,1)andu,v ∈P,we have Hence,λ < λγ <1 forγ ∈(0,1).We apply Lemma 2.6.The proof is similar to the Theorem 3.1,so we omit it. Corollary 3.2Assume that(H1),(H2),(H3)hold.Then the fractional boundary value problem has a unique positive solutionxλinPh.And we have the following conclusions: 1)Fort ∈(0,1),ifthenxλis strictly decreasing inλ,whereγis what appears in (3.2); 2)xλis continuous inλ. ProofApplying Lemma 2.6 and Lemma 2.7,we can obtain the conclusions easily. (H3)′:There existssuch that forx,y ≥0,and for anyt ∈[0,1],λ ∈(0,1),φ(t,λx,λy)≥λσφ(t,x,y)andψ(t,λ−1x,λ−1y)≥λσψ(t,x,y). Corollary 3.3Assume that (H1),(H2),(H3)′hold.Then the solution of BVP (3.4)xλsatisfies Example 4.1Consider the boundary value problem wherea,b ∈(0,1),φ1,φ2∈C[0,1]withφi(t)≥0,i=1,2 andφ2(t)satisties the condition g:[0,∞)→(−∞,0]is the function defined as Notice that Problem (4.1)is a particular case of BVP (1.1),with Obviously,the assumption(H1),(H2)of Theorem 3.1 hold.And by Remark 3.1,gsatisfies the conditions. Now,let’s prove that assumption (H3)holds,where For anyt ∈[0,1],λ ∈(0,1),x,y ∈[0,∞),we have Similarly, Next,we will prove that assumption (H5)holds.For anyx,y,z ∈[0,∞),we have Hence,the assumption (H5)holds. Finally,by using Theorem 3.1 and Remark 3.1,we obtain that Problem(4.1)has a unique positive solutionu∗∈Ph,such that for anyt ∈[0,1]and certain positive constantsm,n.


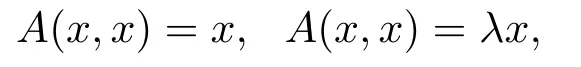
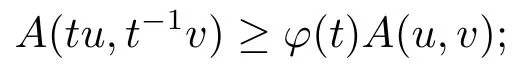

3.Main Results







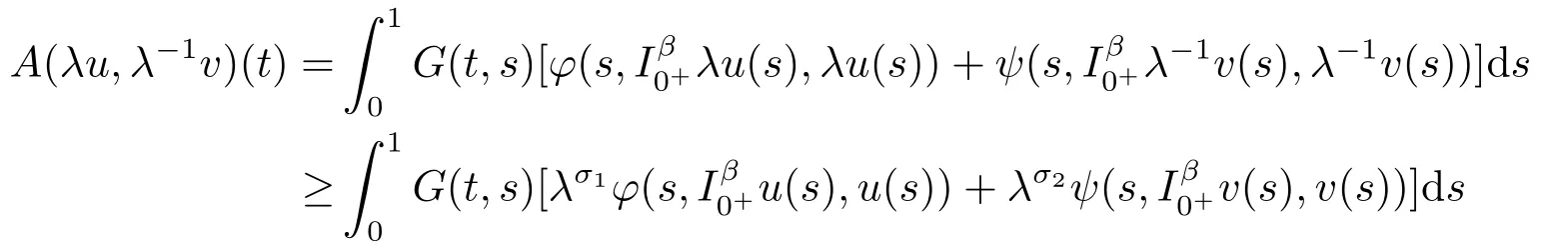










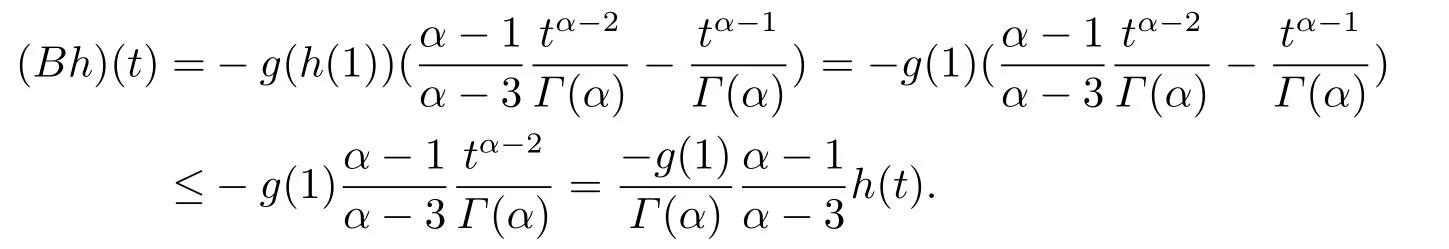









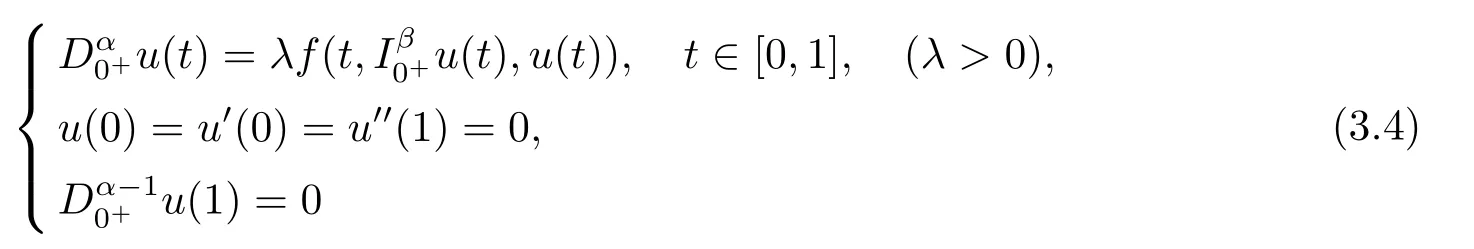
4.Example



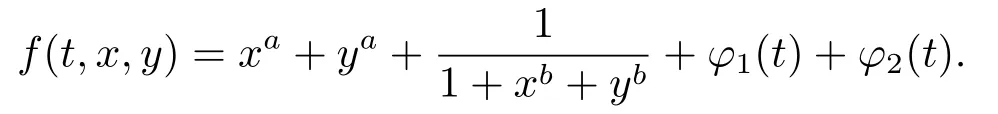





杂志排行
应用数学的其它文章
- Threshold Dynamics of Discrete HIV Virus Model with Therapy
- Solvability for Fractional p-Laplacian Differential Equation with Integral Boundary Conditions at Resonance on Infinite Interval
- Long-Time Dynamics of Solutions for a Class of Coupling Beam Equations with Nonlinear Boundary Conditions
- Existence and Uniqueness of Mild Solutions for Nonlinear Fractional Integro-Differential Evolution Equations
- 基于Markov链的税延型养老保险跨期效用
- 动态投资组合现金次可加风险度量的时间相容性
