一个基于非单调技术的超记忆梯度法
2020-01-10林海婵李靖雅欧宜贵
林海婵,李靖雅,欧宜贵
( 海南大学理学院,海南 海口570228)
1.引言
本文考虑如下的无约束优化问题:

其中f:Rn→R是连续可微的函数.求解问题(1.1)的方法通常采用迭代法[1],其具体的迭代形式如下:

这里αk和dk分别是第k步迭代时的步长因子和搜索方向.为了方便起见,在迭代点xk处,本文用fk表示函数值f(xk),用表示gk梯度∇f(xk),用||·||表示Rn上的2-范数.
共轭梯度法是介于最速下降法和牛顿法之间的一种无约束优化方法.由于共轭梯度法不需要矩阵存储,结构简单,容易编程实现,且具有较快的收敛速度和二次终止性等优点,因此,对该方法的研究已受到人们的广泛重视,目前已成为解决大规模无约束优化问题的有效方法[2−3].记忆梯度方法和超记忆梯度是共轭梯度法的推广[4−5],因此它们也具备共轭梯度法的上述特点.然而,与共轭梯度法相比,这类方法有一个显著的特点,即记忆梯度法和超记忆梯度法在每一次迭代过程中都能够充分利用之前多步的迭代信息去构造新的迭代点,这一特点有助于我们设计出更高效的新算法[6−9].
迄今为止,求解无约束优化问题的共轭梯度法和记忆梯度法绝大多数是采用单调线搜索技术来求步长因子.然而,对那些目标函数出现窄长的弯曲“峡谷”形状时,若此时仍强制要求目标函数在每一步迭代时都严格单调下降,则通常会减缓算法的收敛速率[10],因此,非单调策略应运而生.
最早的非单调线搜索技术是由Grippo等人提出的,它要求步长因子满足如下条件:

其中σ ∈(0,1),m(0)=0,0≤m(k)≤min {m(k−1)+1,M},而M是事先给定的非负整数.大量的数值实验表明:非单调线搜索技术(1.3)及其变形不但可以提高找到全局最优点的可能性,而且可以改善算法的计算效率.随后,研究人员又将该非单调技术及其变形分别与共轭梯度法、记忆梯度法以及其它的优化方法结合起来求解无约束优化问题[11−14].尽管基于条件(1.3)的非单调技术已经得到广泛应用,但该技术仍然存在着缺陷[15].为克服这一缺点,ZHANG和Hager[15]提出了一个新非单调线搜索技术,它用函数的平均值去替换(1.3)式中函数的最大值随后,GU和MO[16]又提出了如下的非单调策略(记为GM-LS):

其中

这里0≤θk ≤θmax<1及σ ∈(0,1).文[16]中的数值试验结果表明:这一改进的非单调策略实用且有效.
根据上述讨论,并受上述文[6,12-13,16]的思想启发,我们在本文给出了一个新的非单调线搜索策略,并以此为基础提出了一个解决无约束优化问题(1.1)的超记忆梯度方法.该方法的主要特点是:它在每一次迭代中总是提供一个充分下降步.这一特性不依赖于目标函数的凸性及其方法所采用的线搜索策略.在较弱的假设条件之下,该方法具有全局收敛性和局部R线性收敛性.数值实验也表明了其有效性.
2.算法描述
本节,我们将给出一个求解问题(1.1)的超记忆梯度算法.为此,我们先定义如下搜索方向:

其中,m是记忆先前的迭代步数,βki(i=1,2,··· ,m)由下式定义:

其中,t ≥1是一常数,rk是一个尺度参数,它的选取按下列方式定义[17]:
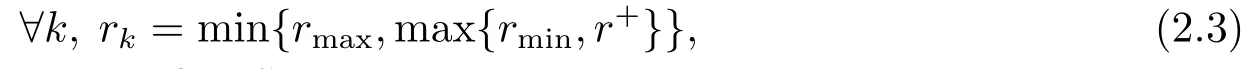
显然,尺度参数rk满足下式:

为了定义我们的算法,我们引进如下的非单调线搜索策略.
修正的非单调线搜索:给定σ ∈(0,1),β ∈(0,1),以及严格单调递减的非负序列 {εk}.令并从 {τk,τkβ,τkβ2,···} 中选取αk使其为满足下列不等式的最大α:


这里0≤θk ≤θmax<1,L为大于0的Lipschitz常数(详情参见后文假设(A2)).
注1显然,当εk ≡0时,(2.5)式就变为文[16]中的非单调策略GM-LS;当εk ≡0且θk ≡0时,(2.5)式就变为经典的Armijo线搜索策略[1].因此,本文提出的非单调线搜索(2.5)可以看做是经典的Armijo 线搜索策略和线性搜索策略GM-LS[16]的推广.同时,由于fk ≤Dk,∀k(参看文[16]引理3.1),故有

从而本文提出的线搜索策略(2.5)更易满足而使得我们可能找到较大的步长因子αk,从而减少了目标函数和梯度函数的调用次数,降低了计算量.下面我们给出本文具体的算法.
算法I
步0 赋初值x0,ε ≥0,D0=f(x0),εk ≥0,r0=1,t ≥1及m ≥0,令k:=0;
步1 计算gk,若||gk||≤ε,停止迭代;
步2 构造满足(2.1)式的搜索方向dk;
步3 由修正的非单调线搜索策略(2.5)计算αk,并令xk+1=xk+αkdk;
步4 令k=k+1,转步1.
注2由文[19]中的引理3.3的结论可知:步3中的非单调线搜索策略(2.5)是适定的,从而算法I是适定的.此外,在算法I中,若选择不同的尺度参数rk,我们就可得到不同的超记忆梯度法.
注3在非单调线搜索(2.5)中,由于Lipschitz常数L事先未知,故在每一次迭代时需要找到一个Lk去估计它.最近,研究人员已经提出一些估计Lipschitz常数L的好方法(见文[18]),在本文的数值试验中,我们使用去估计它,其中L0>0是事先给定的一个较小的正常数.
引理1若dk是由(2.1)-(2.3)定义,则存在正常数c1和c2,使得对所有的k,有

和

证该引理的证明类似于文[12]中的引理1和引理2的证明方法.为保持其完整性,我们仍给出其证明。若k=0,则由定义(2.1)可知,不等式(2.7)和(2.8)成立.
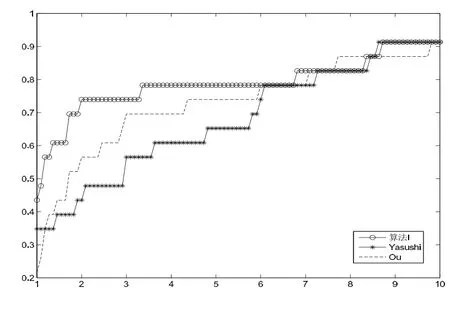
若0 和 由引理1的结论(2.7)和(2.8),我们即可推出下列结论. 引理2若dk是由(2.1)-(2.3)定义,则存在一个正常数c,使得下式成立: 本节我们将分析算法I的收敛性,为此,我们需要如下假设: (A1)函数f在包含水平集的邻域ℵ内下有界; (A2)梯度函数g(x)在ℵ内是Lipschitz连续的,即存在Lipschitz常数L>0,使得 引理3算法I产生的序列 {xk}满足 证由(2.6)式可推出: 我们可用归纳法来证明结论(3.1).当k=0时,结论(3.1)显然成立.假设(3.1)式对于k ≥1成立,则由(3.2)式可知,若能验证下列不等式: 则可得到fk+1≤Dk+1,这表明(3.1)式对于k+1也成立,从而原命题成立. 下面我们将验证(3.3)式的正确性.为此,我们只需验证:存在>0,当α ∈(0,)时,必有 事实上,由归纳法的假设及(2.7)式,我们可推得: 从引理3的证明过程,我们可以推出下列结论. 引理4非单调线搜索准则(2.5)是适定的,即它在有限步内必能找到一个αk,使得该αk满足(2.5)式. 引理5设 {xk}和 {Dk}是由算法I产生的序列,则 且对∀k,有xk ∈L0. 证详见文[19]中引理3.4的证明.证毕. 引理6若假设(A1)和(A2)成立,则存在一个常数η >0,使得 证定义下列两个集合: 为了证明该结论,我们考虑下列两种情形: 情形I 若k ∈K1,则由线搜索(2.5),(2.9)式及我们有 情形II 若k ∈K2,由αk <τk,我们可得令则由线搜索策略(2.5)选取αk的方式可知:不满足(2.5)式,即 利用(3.1)式,我们即可得到 利用微分中值定理,则由(3.8)式我们可推得,存在λk ∈[0,1),使得 即 于是,根据假设(A2)、Cauchy-Schwarz不等式及(3.9)式,我们可推出: 进而有 再由线搜索策略(2.5)、(2.9)及(3.11)式,即可得到 因此,若令η=我们即可由(3.7)和(3.12)式推得不等式(3.6)式成立,证毕. 定理1设 {xk}是由算法I产生的序列.若假设(A1)和(A2)成立,则若非gk=0,必有 证只需证明当gk≠0时,必有(3.13)式成立.用反证法,若结论(3.13)式不成立,则存在一个常数δ >0,使得 由(2.6)及(3.6)式,我们有 即 注意到fk ≤Dk,∀k,从而由假设(A1)可知Dk下有界,再结合及(3.15)式,我们即可推出 显然,上式与(3.14)式矛盾.因此,结论(3.13)成立,证毕. 为分析本文算法I的收敛速度,我们需做如下进一步的假设. (A3)函数f:Rn→R是一个连续可微的强凸函数,即存在一个常数ω >0,使得 引理7[15]若假设(A3)满足,则f存在唯一最小点x∗,而且下列结论均成立 定理2若假设(A1)、(A2)和(A3)都成立,则由算法I产生的无限序列 {xk}收敛于f的唯一最小点x∗.更进一步,若εk=o(||gk||2),则该序列 {xk}至少R-线性收敛于x∗. 证该定理的证明思路源于文[15]中的定理3.1的证法.由定理1及(3.19)式,我们可以直接得到xk→x∗,及g(x∗)=0.下证此定理的第二部分.由(2.7)式及Cauchy-Schwarz不等式,我们有 即 注意到αk ≤τk,∀k,从而结合(3.21)式和Cauchy-Schwarz不等式,有 利用(3.22)式,再结合(2.8)式,我们可推出 因此,由假设(A2)及(3.23)式可推出:存在常数b=使得 利用上面的讨论,我们可以验证下列结论:存在正整数k0和θ ∈(0,1)使得 这表明算法I所产生的序列 {xk}至少是R-线性收敛于x∗的. 现证明不等式(3.25)的正确性,分以下两种情形考虑. 情形I当||gk||2≥b1(Dk−f(x∗))时,由(2.6)及(3.6)式,我们有 又因为εk=o(||gk||2),故存在正整数k0,当k ≥k0时, 结合(3.26)及(3.27)式,我们可得到 此不等式意味着(3.25)式在情形I下成立. 情形II当||gk||2 结合(2.6),(3.27)及(3.28)式,并利用ωb2b1=1−ηb1,我们可推出 上式表明不等式(3.25)在情形II也成立,证毕. 本节,我们将给出算法I的数值结果.为此,我们选取了文[20]中专门用于测试无约束优化问题的10个大规模问题作为测试函数,它们分别是文[20]中第14、21、22、23、24、26、27、30、31、32 个函数.数值实验过程中所用参数分别选为:σ=0.1,β=0.38,θ0=0.1,L0=10−5,r0=1,m=5,t=1,rmin=10−15,rmax=1015,εk=此外,参数θk是按下列递归式来动态地选取: 为检验算法I的有效性,我们还将它与带非单调线搜索的记忆梯度法-Yasushi算法[13]和Ou等人的算法[12]进行了比较.对Yasushi算法,其相关参数选为:m=5,σ=0.1,r0=1=9,σk ≡0.5,v=−0.8,β=0.38; 对算法Ou,其相关参数选为:m=5,σ=0.01,β=0.5,r=0.9,ρ=0.001,L0=10−5,η0=0.5.同时对于算法Ou中参数Ck,由下式定义[15]: 其中 { 所有测试函数的初始点见文[18],而3个算法的终止条件均选为||gk||≤10−5.算法程序都在Matlab7.0环境下运行.详细的测试结果见表1,其中,”Function”表示测试函数,”n”表示测试函数的维数.测试结果是以”k/kf/cpu” 顺序呈现,其中:k代表迭代次数;kf代表函数的调用次数; cpu代表CPU运行时间.同时规定:若算法对测试函数的迭代次数超过10000,或者算法的CPU运行时间超过300秒还未停止,我们就认为该算法运行失败,简记为”F”. 表1 三算法数值实验结果 为更清晰的反映上表的实验结果,我们参阅文[21]提出的有关性能线的定义,分别为表1中的k、kf及cpu三种数据做出性能线描述图,详情见图1、图2、图3. 图1 三算法的k性能线描述图 图2 三算法的kf性能线描述图 图3 三算法的cpu性能线描述图 从以上性能线描述图1、2和3,我们可观察到事实:1)对于迭代次数而言,算法I的执行效率略优于算法Yasushi,但它们都好于算法Ou; 2)对于函数值的调用次数,算法Yasushi和算法Ou执行效率大致相当,但它们稍劣于算法I; 3)对于运行时间,算法I的执行效率要优于其它2个算法.因此,综合以上三方面的事实,我们认为:算法I是可以同其它两个算法相媲美. 当然,我们还不能从上述有限的数值测试结果得出一般性的结论.对基于非单调技术的优化方法的研究,尤其是对大规模问题的超记忆梯度方法的深入探讨将是我们今后的任务.



3.算法的收敛性分析




















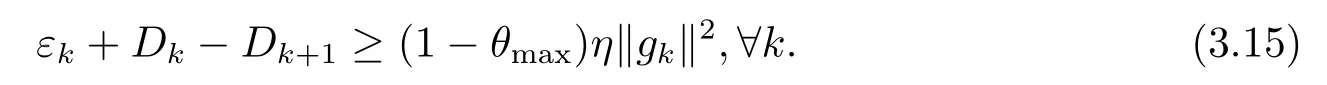















4.数值实验






猜你喜欢
杂志排行
应用数学的其它文章
- Threshold Dynamics of Discrete HIV Virus Model with Therapy
- Solvability for Fractional p-Laplacian Differential Equation with Integral Boundary Conditions at Resonance on Infinite Interval
- Long-Time Dynamics of Solutions for a Class of Coupling Beam Equations with Nonlinear Boundary Conditions
- Existence and Uniqueness of Mild Solutions for Nonlinear Fractional Integro-Differential Evolution Equations
- 基于Markov链的税延型养老保险跨期效用
- 动态投资组合现金次可加风险度量的时间相容性
