考虑气象因子的区域电网梅雨期负荷预测
2020-01-10苏宜靖于竞哲
苏宜靖,谷 炜,赵 依,董 立,蒋 琛,于竞哲
(1.国网浙江省电力有限公司,杭州 310007;2.长安大学 电子与控制工程学院,西安 710021;3.浙江大学 电气工程学院,杭州 310027)
0 引言
我国东南沿海地区每年春、夏交替期间,受副热带高压影响而持续产生降雨的天气称为“梅雨天”。梅雨的持续时间、气温、湿度及降水量直接或间接地影响着区域电网的负荷情况[1]。短期负荷预测需要综合考虑这些气象因子,才能对未来数天的负荷水平进行较为精准的预测。梅雨期是电力负荷由春季较低水平向夏季高峰水平过渡的时期,特别是出梅期前后,气温快速上升,负荷也会呈大幅上涨趋势。较好的短期负荷预测能够为电力调度部门优化发电机组的配置、合理化电网上下调备用和最优化潮流分布提供重要参考[2],这直接关系着电网调度的经济性和安全性。
目前负荷预测的相关算法及手段较为丰富,文献[3]提出了一种基于L-M优化的BP(反向传播)神经网络负荷预测算法,能较好地预测特定日的负荷变化趋势。文献[4]引入有效度和相对熵的概念,利用4种预测模型对负荷进行组合预测,具有较高的预测精度。文献[5]采用模糊化聚类分析方法建立了考虑数值天气预报下的母线负荷预测模型,为负荷预测的实用化提供了重要支持。这些负荷预测模型及研究方法为本文研究提供了重要参考。
本文统计分析了近两年某区域梅雨季节气象条件及负荷变化特点,综合考虑气象因子与负荷的相关性。分别建立了基于Elman和BP的2种神经网络模型,筛选可作为预测样本的数据节点,对比2种模型预测结果,并深入分析了负荷预测误差的产生原因。
1 综合气象因子与负荷的关系
1.1 负荷特性解析
随着社会城市化进程的推进,区域电网负荷受气象因素的影响愈加明显。特别是沿海地区在出梅期前后,气温变化明显,天气由阴雨转为晴朗,对气象变化敏感的负荷也会有明显的提升。依据负荷变化特性,可以将其解析为基础负荷、气象敏感负荷及随机波动负荷[6],如式(1)所示。

式中:p为实时负荷;pb为基础负荷;pw为气象敏感负荷;pr为随机波动负荷。
基础负荷主要与社会经济发展水平相关,在较短的时间范围内体量基本保持稳定,与生产生活的用电规律关系紧密,而与气象因素关系不大[7]。每年春秋季的气候条件相对温和,负荷随气象变化相对较小,此时区域电网实时负荷可视为基础负荷。
气象敏感负荷是指易受气象条件影响的负荷,气象条件包括天气、温度、湿度、降水、风速、光照等。每年夏季或冬季,电网空调负荷随气象条件的变化较大,此时较春秋季负荷增加的一部分量即为气象敏感负荷。为了提高梅雨期负荷预测的精确度,应着重考虑气象因子对pw的影响。
随机波动负荷是受偶然事件影响而产生的负荷波动分量,包括突发故障、短时限电等,负荷预测可不考虑这类分量。
1.2 综合气象因子处理
各类气象条件因子对电力负荷均会产生不同程度的影响,如夏季气温上升导致降温负荷增大,降雨能够有效降低气温从而降低电力负荷,湿度与风速影响着人体的舒适程度进而影响调温除湿负荷,天气条件会影响光照强度,而光照的强弱又影响着光伏出力和照明负荷。由此可知,气象条件对电力负荷的影响是综合性的[8]。
为了有效利用各类气象因子,可以通过CIHB(人体舒适度指数)和THI(温湿指数)来量化气象条件[9]。CIHB是指人们未使用保暖或降温措施时在当前气象条件下感觉到的舒适程度[10],计算公式如式(2)所示。

式中:T为温度;Rh为相对湿度;v为风速,梅雨期可取1.0~3.0 m/s。
THI是一种人为提出用来表示电力负荷与气象条件之间的关系因子,计算公式如式(3)所示。
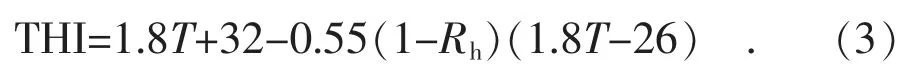
除利用上述指数外,考虑梅雨期多阴雨天气,光照强度中等,风速较小且变化不大,还应重点关注最高/最低温度、相对湿度和降水量对日最大/最小电力负荷及电量的影响。
1.3 综合气象因子与负荷的相关性
为了研究梅雨期气象因子对负荷的影响,同时保证预测的正确性与精确性,需要对样本数据进行相应的处理,即剔除节假日及台风日数据。以2016年、2017年梅雨期某区域电网数据为例,对比分析了数据处理前后气象因子与负荷的相关性,详见表1。
剔除特殊日数据后,负荷与气象因子的相关程度明显加深。温度与负荷相关性最强,是影响梅雨期负荷水平的关键因素,负荷随着气温的升高而升高;降水量和相对湿度对负荷的影响相对较小,相关性不强,但大体上也具有降水量越小、相对湿度越大则负荷越高的趋势;CIHB和THI与负荷具有较强的相关性,两类指标数值越高,实时负荷也随之抬高,可作为影响因子来指导负荷预测。
根据上述各气象因子与实时负荷的相关程度,可以设定3组不同气象因子的数据源:一是仅考虑日最高/最低气温作为负荷预测的单一数据源;二是同时考虑日最高/最低气温、降水量、相对湿度因素作为负荷预测的基础数据源;三是考虑综合气象因子作为负荷预测的综合数据源。在预测模型中支持将单一、基础和综合3组数据的预测结果横向对比分析。

表1 综合气象因子与负荷的相关性对比
2 人工神经网络预测模型的建立
2.1 Elman神经网络算法原理
与BP神经网络[11]相比,Elman神经网络存在一个特殊的关联层,作用是存储隐含层单元前一时刻的输出值,联接记忆的数据作为下一次隐含层的计算输入值,模型结构见图1。这种状态的延迟效应使神经网络具备良好的记忆性能[12]。

图1 Elman神经网络模型结构示意
假设ui,vj,tl,yk分别为输入层、隐含层、承接层和输出层的计算结果,则网络传递过程的计算公式如式(4)所示。

式中:xi为输入变量;n,m,q分别为输入层、隐含层和输出层设置的神经元个数,承接层的神经元个数与隐含层相同为m;w1ij,w2jk,w3lj分别为输入层i至隐含层j、隐含层j至输出层k、承接层l至隐含层j的连接权值;T为迭代计算次数;f和g分别为隐含层和输出层神经元的传递函数,可选择线性函数或sigmoid函数。承接层作用是记录上一次对应隐含层计算值。
由于Elman神经网络一般采用与BP网络训练相同的梯度下降算法,w1ij和w2jk的修正过程相同,补充w3lj的修正过程如式(5)所示。

式中:Δw3lj为对应承接层至隐含层连接权值的修正量;dk为目标结果值。
2.2 Elman神经网络算法流程
Elman神经网络学习算法流程如图2所示。

图2 Elman神经网络学习算法流程
Elman神经网络通过内部承接层的反馈作用,存储并有效利用历史数据,具备动态响应特性,能够实现静态或动态系统的建模,适合于类似持续时间序列的负荷预测[13]。但网络的训练过程需要迭代的次数较多,存在收敛较慢的情况。
3 梅雨期负荷预测算例
本文收集了东南沿海某区域电网近两年的梅雨期气象及负荷数据。梅雨期区域间的选择参考省级气象局发布的入梅和出梅时间,分别为2016-05-25—07-25和2017-06-09—07-13。上述时间段的初始数据均需要经过预处理与筛选,剔除节假日及台风的影响。在气象输入数据上,分别采用了单一、基础和综合气象因子3组数据以作对比分析。在选取预测模型上,分别采用BP和Elman神经网络算法并选取合适的模型训练方法。其中,2016年的数据作为负荷预测模型的训练样本,在考虑基础负荷增长并进行适当修正后,将2017年的数据作为测试样本。
3.1 气象数据的选取与预处理
相较于工作日,节假日工业负荷与商业负荷的变动较大,直接影响了基础负荷部分[14];同时台风天气日负荷水平变动较大,对电网而言存在不确定性因素,如线路跳闸、临时停电等。进行梅雨期负荷预测时可以暂不考虑上述数据,而应筛选出正常工作日的数据作为本次负荷预测的样本数据,需要剔除节假日与台风所造成影响的数据。以2016年该区域梅雨期气象数据为例,气象数据处理后的结果如表2所示。
为了预防神经元在计算过程中发生数据饱和溢出,应先将模型的输入量进行归一化处理,将输入数据限制在[0,1],待模型预测完成后对输出量进行反归一化处理,以得到负荷预测的结果。数据归一化和反归一化计算如式(6)所示。

式中:zi为原始数据;ai为归一化后的数据;zmin,zmax分别为原始数据的最小值和最大值。
3.2 神经网络模型的训练
依据上述神经网络模型的原理与方法,在MATLAB中分别建立双隐含层的BP神经网络模型和单隐含层的Elman神经网络模型。训练精度均设置为0.001,训练步长设置为0.001。隐含层传递函数均设置为“tansig”的非线性函数,输出层传递函数均设置为“purelin”的线性函数,承接层传递函数设置为“purelin”的线性函数。两者的训练过程均采用梯度下降算法,以优化训练过程。
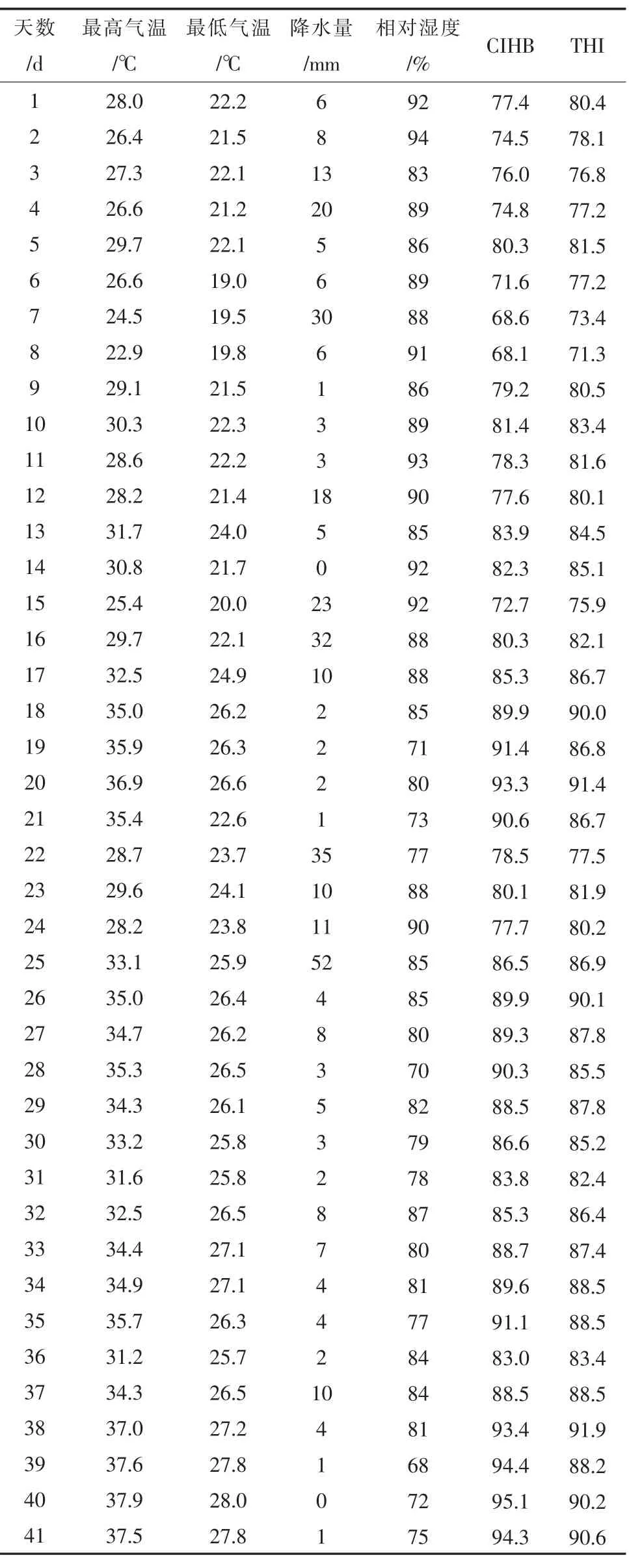
表2 2016年某区域梅雨期气象数据
选择负荷预测模型的输出量均为日最大负荷、日最小负荷、日电量。为了对比不同输入量对负荷预测结果的影响程度,选取最高气温、最低气温、日降水量、日平均相对湿度作为基础气象因子负荷预测模型的输入量;选取CIHB和THI作为综合气象因子负荷预测模型的输入量;选取最高气温、最低气温作为单一气象因子负荷预测模型的输入量。
以2016年梅雨期该区域的日电量为例,2种模型的训练结果如图3所示。可以发现,无论BP神经网络还是Elman神经网络的训练结果基本拟合了实际日电量的变化曲线。对日最大负荷/最小负荷可以采用同样的方法进行拟合。

图3 BP及Elman神经网络训练结果
3.3 考虑年度负荷增长趋势的预测结果处理
随着经济社会的发展,负荷水平及日用电量总体呈上涨趋势。假设2017年相较2016年基础负荷和气象敏感负荷的增长比例分别为α和β,则考虑气象因素后的负荷如式(7)所示。

式中:p2016,p2017分别为2016年和2017年的电力负荷;p2016b,P2016w分别为2016年的基础负荷和气象敏感负荷;f(·)为气象影响系数。
神经网络训练算法得到的是2016年的负荷数据,考虑年度负荷增长趋势后,将预测结果进行转换得到式(8)。
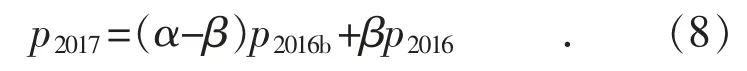
近年来,基础负荷增长比例α与气象敏感负荷增长比例β近似等于总体负荷增长比例。利用2016和2017年3—4月每日最大调度口径负荷按日取平均并相除计算得到,如2016年3—4月的日最大平均负荷约为5 000万kW,2017年3—4月的日最大平均负荷约为5 200万kW,则总体日负荷增长比例约为1.04。同理,可计算得到日电量增长比例约为1.08。可代入式(8),修正下一年度的负荷预测结果。
经选择与预处理后,2017年梅雨期相关气象数据如图4所示。

图4 2017年某区域梅雨期气象数据
在2种负荷预测模型中分别输入2017年梅雨期基础气象变化数据,并经式(8)换算后,得到日负荷及日电量预测结果如图5所示。

图5 BP及Elman神经网络负荷预测结果
结合图4、图5可知,从气象数据上看,刚进入梅雨期,连续的阴雨天气,降水量骤升,使气温开始下降至最低点。随后气温开始回升,湿度下降,温湿指数及人体舒适度逐渐上升,直至梅雨期结束。从负荷数据上看,刚进入梅雨期,日负荷及日电量下降,并在一定时间内保持一定的水平,随后在出梅期前后,负荷及电量快速上升,负荷数据变化情况基本上与气象数据变化一致。结合气象因子的BP和Elman神经网络算法对梅雨期的负荷预测结果基本符合实际情况。
4 负荷预测结果分析
为了评价不同神经网络算法及输入量对预测结果的影响,需要将预测值与原始数据进行对比,得出误差后,对预测结果的准确度进行定量分析。
4.1 预测准确度分析与结果评价
选择合理的误差评价指标,能够有效对比不同的预测结果[15]。本文主要采用MAPE(平均绝对百分比误差)和可决系数法2种方法对负荷预测结果进行准确度分析。
MAPE的计算公式如式(9)所示。MAPE越小,说明预测结果与实际偏离越小,精度越高。

式中:Pi为负荷预测结果数据;Pi0为实际负荷数据;N为样本数。
可决系数法是通过RSS(残差平方和)及TSS(总平方和)计算得到的,计算公式如式(10)所示。可决系数R2被限定在[0,1],结果越靠近1说明预测结果越接近实际结果。

采用不同神经网络算法及不同输入量的负荷预测准确度统计如表3所示。
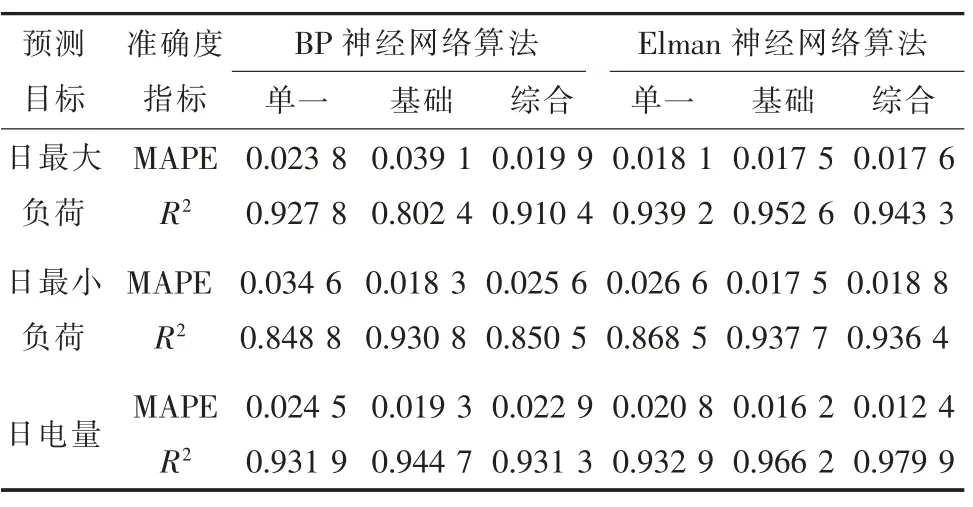
表3 负荷预测准确度统计结果
由表3可知,对于同一种数据输入量类型,Elman神经网络算法无论是MAPE还是R2指标都优于BP神经网络算法,说明Elman算法在梅雨期负荷预测上更具有优势。在同一种算法下,采用不同的数据处理方法,如运用基础气象数据和综合气象数据比单一来源数据的负荷预测结果更加精确。对于不同的预测目标,预测日最大负荷及日电量的结果比日最小负荷预测结果更为准确。总体而言,本文提出的Elman神经网络算法在考虑基础或综合气象因子情况下,对梅雨期日最大/最小负荷、日电量均具有良好的预测特性。
4.2 负荷预测误差产生原因分析
上述梅雨期负荷预测结果相比实际测得值存在1%~3%的误差,而短期负荷预测误差是不可避免的,本文预测误差的来源主要包括:
(1)历史气象数据统计不全面、不精确。本文只考虑了区域电网气象条件的整体水平,并未对下属各地区气象情况进行分时段精确统计,而且存在部分天气数据缺乏的情况。
(2)神经网络模型通过历史负荷数据来推断下一年的负荷数据,是一种近似的估算,只能反映负荷变化的趋势,而无法精确计算。
(3)在实际电网运行中,负荷的波动是一种随机过程,多种外界因素比如突发事故、光伏风电出力骤增都可能对电网产生影响,这些在预测模型中都无法精确考虑。
5 结语
针对区域电网负荷梅雨期前后快速增长的特点,本文提出了考虑气象因子的区域电网梅雨期负荷预测方法,分别构建了基于BP神经网络和Elman神经网络的短期负荷预测模型。以2017年梅雨期负荷水平为例,对比不同气象因子预测结果的差异,发现考虑基础和综合气象因子数据能够有效提高预测精度,同时Elman较BP神经网络算法在MAPE和R2指标上均占优势。结果表明,本文提出考虑气象因子的Elman神经网络负荷预测模型,对梅雨期的负荷具有预测精度高、适应性强、使用价值较好等特点,可用于指导实际负荷预测。
