基于负荷轴工况划分的发电厂关键设备非平稳状态监测
2020-01-10沙万里陈军豪赵春晖
沙万里,陈军豪,赵春晖
(1.浙江浙能嘉华发电有限公司,浙江 嘉兴 314201;2.浙江大学控制科学与工程学院,杭州 310027)
0 引言
在我国的电源结构中,火电一直是主力电源。截至2018年的统计数据,火电发电量占全国发电量的比例超过60%,其中燃煤发电是火电的主体,因此火电机组的安全稳定运行对保障我国电力供应至关重要。热力系统作为火电机组的重要组成部分,是一个极其复杂的工业系统,整个工业过程生产流程长、单元装置多、空间分布广、安全要求高,其中可能会发生的故障复杂多样。对热力系统关键设备进行状态监测能够帮助发电厂充分了解设备运行状况、及时进行故障排查与检修、减少停机检修的时间,从而提升生产效率、防止生产事故的发生。因此,迫切需要对热力系统的关键设备实施有效的状态监测。
在火电热力系统实际运行过程中,负荷的频繁变化会使得热力系统关键设备部分运行参数的均值和方差随时间发生改变,呈现出明显的非平稳特性,由此导致机组的变工况问题非常普遍。频繁出现稳态工况与过渡工况交替的现象,给运行异常的及时监测带来了较大困难。一方面,故障特征很容易被非平稳趋势所掩盖。另一方面,传统的状态监测方法不能准确地描述非平稳变量间的关系,由此可能导致错误的监测结果。此外,由于变工况现象,尤其是过渡工况的存在,实际火电热力系统运行过程的状态监测相比单一稳态工况下的状态监测难度更大要求更高,存在很多问题和挑战需要作深入研究。
截至目前,已有的状态监测方法可以归为2类:基于模型的[1-2]和数据驱动的[3-5]。其中,数据驱动的状态监测方法不依赖过程知识,能够通过分析过程数据、提取其中所包含的过程信息来描述过程的运行状态,从而实现有效的过程监测。因此,数据驱动的方法被广泛运用于解决火电热力系统状态监测问题[4,6-10]。针对非平稳过程的监测方法,较为常用的有2种:基于协整分析的方法[10-13]和基于工况划分的方法[6-7]。
Chen等人[11]首先将协整分析方法运用于一个工业蒸馏单元的状态监测。Li等人[12]使用协整分析导出了多个残差变量,并计算了T2统计量的值来检测异常行为。Zhang等人[10]提出了一种基于协整分析和主元分析的两级非平稳过程状态监测方法。在下级模型中,首先区分平稳变量和非平稳变量,使用主元分析和协整分析分别对平稳变量和非平稳变量进行监测。为了对平稳变量和非平稳变量间的关系进行监测,文章利用协整分析得到的平稳残差序列和平稳变量一起构成新的数据矩阵,在上级模型中使用主元分析来进行监测。但是,协整分析仅仅能够应用于具有协整关系的非平稳变量的监测,对不具备协整关系的非平稳变量的监测无能为力。
黄孝彬等[6]在分析火电机组负荷变化特点后提出,火电机组的典型运行状况可以归纳为大部分时间是处于稳定工作状态,而不同稳定状态是连续变化和过渡的,进而提出了一种累计递推的PCA建模方法,即“不断的积累数据并用递推的方式估计变量的统计特性:方差和相关系数矩阵。当递推的结果表现为变量统计参数的估计值趋于稳定时,此时可以认为用这些数据建模就能抓住过程的变动特性。”[6]文章将该方法应用于锅炉过程传感器的故障检测,取得了较好的效果。华北电力大学的牛征等人[7]针对火电厂变工况的特点,提出了另外一种工况划分思路:首先用K-means聚类方法将数据进行聚类,认为得到的各个类即为不同稳态下的数据集;然后对各个数据集分别建立主元模型;最后将待监测样本进行模糊划分,提出了一种模糊动态主元模型的方法计算其适用的主元模型,并在锅炉数据上验证了该方法的有效性。此外,许仙珍等[14]利用混合高斯模型来对多工况过程进行工况划分,然后对每个工况建立主元分析模型,实现了对多工况过程的状态监测。以上方法都利用了聚类的方法来进行工况划分。由于聚类时会利用多个变量而不仅仅是负荷这一变量,因此,划分的工况内很可能存在着负荷差距很大的样本,而这明显是不符合实际情况的;其次,聚类算法的聚类标准并不是针对状态监测这一问题提出的,因此,使用一般聚类算法来进行工况划分很有可能会对后续的状态监测带来不利影响。
为解决上述方法的不足,本文提出了一种基于负荷轴工况划分算法的非平稳状态监测方法,来解决火电关键设备的非平稳状态监测问题。首先,考虑到同一工况下负荷必然是相近的,为避免将负荷差别较大的样本划入同一工况而负荷差别较小的样本划入不同工况,本文所提的方法将时间轴变为负荷轴,即,将初始时以时间顺序排列的样本集按负荷从小到大重新构造。其次,对于过程监测来说,以监测模型的性能优劣来指示工况划分更为合理,因此,提出基于负荷轴的工况划分算法来进行工况划分。划分完毕后,所得到的各个工况内的数据可近似认为是平稳的,且具有相似的特性。因此,可以利用主元分析方法在每个工况内分别建立状态监测模型。最后,根据新来样本的负荷调用相应的监测模型,进行在线的状态监测。
1 基于负荷轴工况划分的非平稳状态监测方法
本文提出的基于负荷轴工况划分的非平稳状态监测方法,包括4个部分:构造负荷片以进行工况划分;基于负荷片的自动有序工况划分;基于主元分析的多工况建模方法;在线监测方法。
1.1 负荷片构造
考虑火电热力系统某设备数据集X(N×J×P),其中N表示样本数,J表示变量数,P表示负荷。在每一个负荷p处,可以得到一个二维的数据矩阵Xp(np×J),称之为负荷片,作为基本数据分析单元,它是由所有负荷等于p的样本点组成的矩阵。在每个负荷片内,可以认为过程特性未发生显著变化,通过分析每个负荷片的数据特性,可以得到过程在每一个负荷处的内在运行状态以及过程状态随负荷的变化情况。
在实际应用时,无法对负荷进行无限细分,因此使用一个足够小的负荷区间[p,p+Δp]内的样本集合来代替负荷p处的样本集合作为基本数据分析单元是合理的。而由于数据量的限制,在每一个负荷区间[p,p+Δp]内得到的二维数据矩阵很可能存在样本数量不足的问题,不足以揭示同一负荷区间下的统计波动特性,因此,还需要对构造的基本数据分析单元进行一些调整。将样本数较少的基本数据分析单元与其相邻负荷区间的基本数据分析单元进行合并。如果合并过多的基本数据分析单元,会使得负荷方向上的波动信息过大而导致同一负荷区间下不同样本间的波动特性被掩盖。一般来说,为了提供可靠的数据标准化信息,通常基本数据分析单元内的样本数要等于过程变量个数的2~3倍[15]。在每个调整后的基本数据单元中,可以近似认为过程特性未发生显著变化,能够提供较为可靠的数据标准化信息。
1.2 基于负荷片的自动有序工况划分
考虑到相同的工况内,负荷相近、过程特性变化较小、变量间的相关关系近似相等,因此,利用变量间相关关系的相似程度来对调整后的负荷片进行合并,将过程特性相似的相邻负荷片合并,得到不同工况,分析每个工况的过程特性,分别建立状态监测模型,可以提高对监测过程的理解及监测结果的准确性。
针对间歇过程的多时段特性,Zhao等[16]提出了一种SSPP(自动步进有序时段划分)方法,通过不断比较时间片模型和由时间片依次构成的时间块模型的SPE指标来确定时段划分点。由于SPE指标可以灵敏地反映变量相关性并且直接和监测性能相关,该方法有效改善了监测性能。李文卿[15]针对小样本情况,将SSPP算法进行了推广,提出了一种GSSPP(基于泛化时间片的步进有序时段划分)算法,通过衡量泛化时间片中的数据特性对监测模型性能的影响进行时段识别。
对于过程监测来说,应当以监测模型的性能来指示工况划分。因此,借鉴上述GSSPP算法划分间歇过程时段的思想,提出一种基于负荷轴的有序工况划分算法,以火电机组热力系统关键设备的负荷变量来指示工况划分,从而识别出不同的工况。基于负荷轴的有序工况划分算法的具体步骤如下:
(1)步骤1:构造负荷片。以一个较小的Δp为间隔,划分负荷区间为[Pmin+(i-1)Δp,Pmin+iΔp],i=1,2,…,。负荷片记为Xk,k=1,2,…,,每个负荷片由负荷处于相应负荷区间的所有样本构成。
(2)步骤2:对负荷片进行合并调整,使得每个负荷片内样本数为过程变量个数的2~3倍。将调整后的负荷片记为Xk,k=1,2,…,K,并在每个负荷片内对其进行标准化,记为(nk×J)(k=1,2,…,K)。
(3)步骤3:对每个负荷片进行PCA建模。将步骤2中经过标准化处理的每一个负荷片矩阵(nk×J)(k=1,2,…,K)进行PCA分解,从而建立PCA模型:
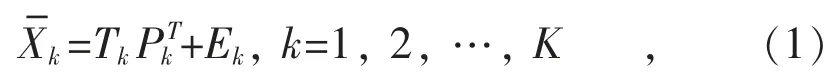
式中:Tk(nk×Rk)与Pk(J×Rk)代表保留Rk个主元变量的得分矩阵和负载矩阵;Ek为残差矩阵。这里,保留的主元个数按以下方法确定:计算每一个负荷片PCA模型累计方差达到99%的主元个数,选取其中出现次数最多的主元个数作为所有负荷片PCA模型的主元个数,记为R,即Rk=R(k=1,2,…,K)。
(4)步骤4:负荷片PCA模型SPE统计量控制限确定。对每一个负荷片PCA模型,计算其SPE统计量控制限。计算公式如下:
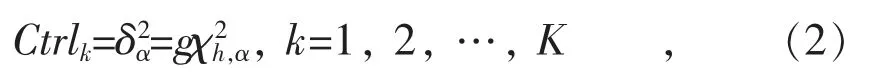
(5)步骤5:负荷段PCA建模。从第一个负荷片开始,依次将下一个负荷片与之前的负荷片组合在一起,得到负荷段数据矩阵,其中i从1开始,j也从1开始。对负荷段数据矩阵Xi,j进行PCA分解,获得负载矩阵Pi,j(J×R)。使用负荷段PCA模型负载矩阵Pi,j(J×R)对负荷段内每一个负荷片进行分解,并在每一个负荷片内,计算SPE统计量及其控制限。这代表了负荷段PCA模型对其区间内的每一个负荷片的重建能力。
(6)步骤6:比较负荷段PCA模型中每一个负荷片的SPE控制限与每一个负荷片单独建立的PCA模型的SPE控制限Ctrli,Ctrli+1,…,Ctrli+j。找到连续3个负荷片呈现出时的j,这就意味着新加入的第j个负荷片对负荷段的PCA模型及其监测性能有重大影响,导致负荷段PCA模型的准确性相比负荷片PCA模型有显著降低,也就是说,只能将第i个至第i+j-1个负荷片划分在一起,这样便划分出了一个工况。α是一个被称为宽松因子的常数,反映了与负荷片PCA模型相比,允许负荷段PCA模型监测准确度损失的程度。
(7)步骤7:更新过程分析数据,迭代完成所有工况的划分。移除已划分好的工况所包含的负荷片,将剩余负荷片作为步骤5的新的输入,再次进行步骤5和步骤6,划分出下一个工况。迭代进行,直至没有负荷片剩余。
通过以上步骤,可以将不同工况所对应的负荷区间划分出来。接下来,就可以在每一个工况内分别建立一个监测模型,根据新样本的负荷值所处区间来调用相应的监测模型,实现过程监测。
需要注意的是,宽松因子α的取值将会直接影响工况的划分结果。α越大,意味着负荷段PCA模型所允许的准确度损失越大,那么每个负荷段将包含更多的负荷片,从而会获得更长的负荷段,即划分出的工况数会更少;而α越小,意味着负荷段PCA模型所允许的准确度损失越小,监测模型对每个负荷片的表征就越精确,从而得到的是更短的负荷段,即划分出的工况数会更多。因此,α反映的是模型准确度和模型复杂度的一种折中。一般来说,α的值是通过比较验证集上的监测效果来确定的,α的取值要使得每个工况包含合适的过程运行模式,保证对过程特征变化的敏感性。
1.3 基于主元分析的多工况建模方法
在工况划分完毕之后,将每个工况内的负荷片整合成为一个数据矩阵,记为Yi(Ni×J),i=1,2,…,M,其中,M为划分出的工况个数。在每个工况内建立PCA模型,计算出T2和SPE统计量控制限。Yi的每一行代表一个样本点,每一列代表一个变量序列。具体步骤如下:
(1)步骤1:使用SVD(奇异值分解)的方法建立主元分析模型:
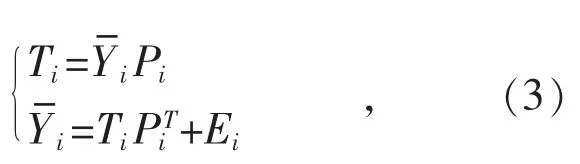
式中:Pi是负载矩阵;Ti是相应的得分矩阵;Ei是提取主元后留下的残差矩阵。Ri表示保留的主成分个数,由累计方差贡献率准则来确定。
(2)步骤2:计算T2和SPE统计量控制限。表示第i个工况下置信度为α的T2控制限;表示第i个工况下置信度为α的SPE控制限。当T2和SPE位于控制限内时,认为过程是正常的,如果超出控制限,则表明有故障发生。2个统计量的控制限计算公式如下:
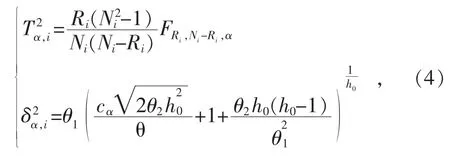
式中:FRi,Ni-Ri,α是带有Ri和Ni-Ri个自由度、置信水平为α的F分布临界值;(i=1,2,3);,λj为的协方差矩阵S的特征值,cα为标准正态分布在置信水平α下的阈值;Ri为所建立的PCA模型保留的主元个数;J为所含有的变量个数;N为当前工况下的样本数。
(3)步骤3:在实际应用中,使用1个指标比2个指标更为方便,因此,计算合成指标控制限。合成指标将SPE和T2用以下方式进行了融合[17]:
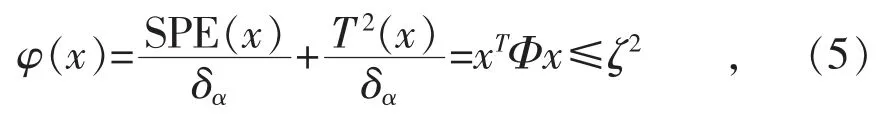

1.4 在线监测方法
在上述步骤中,根据过程特性建立了各个工况下的状态监测模型。在线应用时,首先根据新来样本yt(J×1)包含的负荷值确定其所处的工况,然后选取相应的监测模型来进行监测。具体步骤表述如下:
(1)步骤1:首先,根据负荷值确定其所属的负荷片,假设其处于第j个负荷片;其次,根据工况划分结果,确定yt所处的工况,假设yt处于第i个工况。
(2)步骤2:根据第j个负荷片的离线数据Xj的均值和方差对yt进行标准化,然后,由第i个PCA模型来进行监测。在线监测统计量定义为:
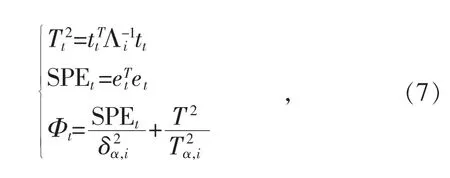
当统计量在控制限以下时,样本被认为是正常的。否则说明样本存在异常,检测到了故障。
2 实验分析
2.1 数据说明
一次风是指煤粉燃烧时与煤粉一起送入炉膛的空气,对锅炉的燃烧起主导作用,一次风机是锅炉的重要辅机之一。本文数据集来源于浙江省某集团下属发电厂,选取了一次风机正常运行时采集的12 364个样本,相邻样本间的时间间隔为3 min,其中70%作为训练集,用来建立监测模型,30%作为验证集用来确定α的取值。每个样本含有36个过程变量,简单起见,在表1中只列出前14个变量。训练集记为Xtrain(655×36),验证集记为Xverify(3 709×36)。此外,选取了一次风机正常运行时另外采集的900个样本作为测试集1,相邻样本间的时间间隔为3 min,记为Xtest1(900×36);选取一次风机在故障发生前采集的500个样本作为测试集2,相邻样本间的时间间隔为3 min,记为Xtest2(500×36)。此处,一次风机发生的故障为从第100个样本点处开始电机轴承温度升高。
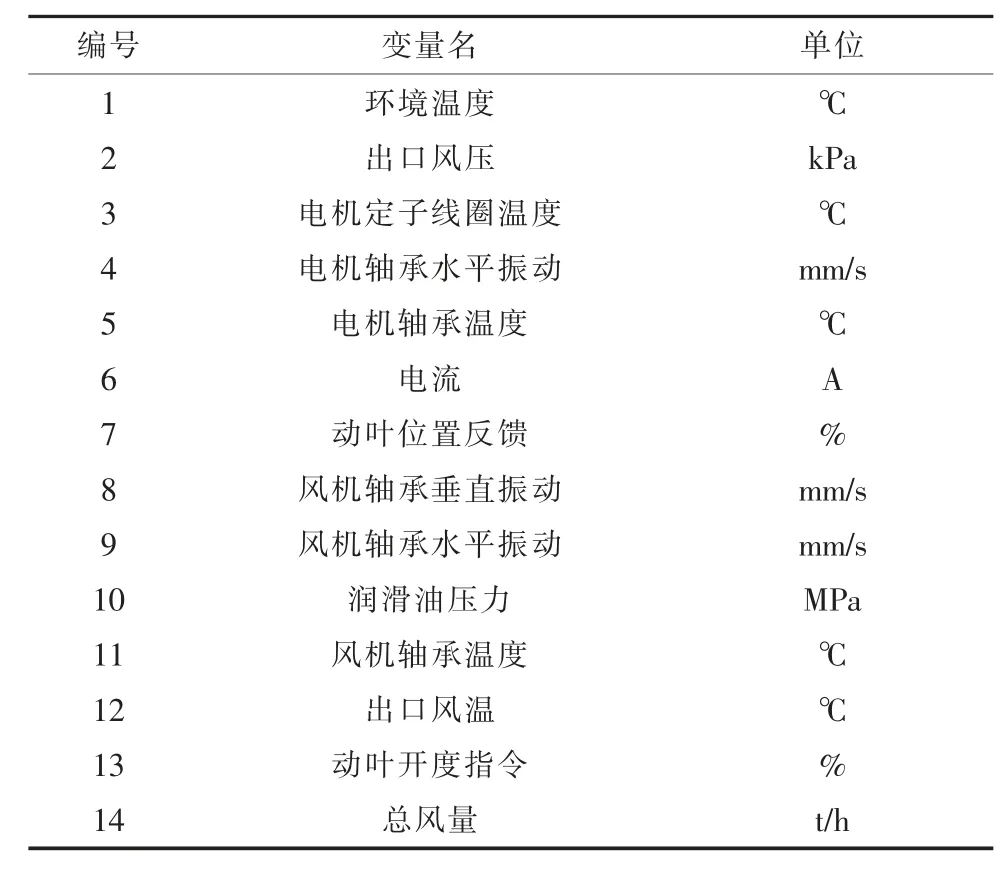
表1 一次风机部分变量
2.2 建模过程
使用训练集Xtrain(8 655×36)来建立监测模型的第一步便是划分工况。根据过程机理知识,对于一次风机来说,可以使用出口风压来作为区分其不同工况的划分变量,但根据本文所提的算法,计算监测统计量时会排除划分变量,为保留尽可能多的信息,本文考虑构造一个与出口风压十分相关的变量代替出口风压作为划分变量,以使得计算监测统计量时出口风压也被考虑在内,分析训练数据可知风压开方后的值与风压的相关系数达到了0.99,因此,这里将出口风压开方后的值,作为划分变量对工况进行划分,记为sqrt(风压)。
训练集Xtrain(8 655×36)包含了足够多的运行工况,其中sqrt(风压)和一次风机电流随时间变化如图1所示。由图1可知,sqrt(风压)随时间波动相当频繁,存在明显的非平稳特性,经检验亦为非平稳变量。相应地,过程变量例如一次风机电流也随之产生变化。
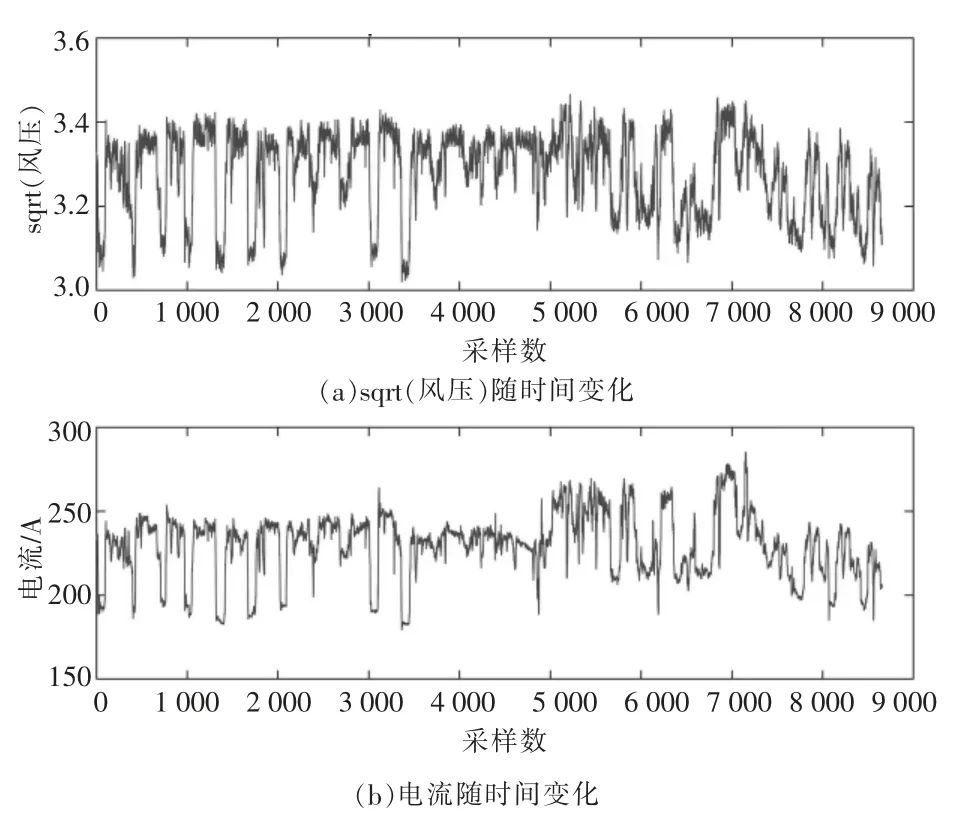
图1 正常运行时sqrt(风压)及一次风机电流随时间变化
为进行工况划分,首先,将sqrt(风压)最小值至最大值区间等分为了40个小区间,形成40个基础数据矩阵。考虑到每个基础数据矩阵内的样本数量需要为变量数的2~3倍才能较好地使用PCA方法提取到数据中的信息,因此,在这里确定每个基础数据矩阵内的最小样本数为80。之后,需要将不满足最小样本数量要求的基础数据矩阵进行合并,最终得到满足要求的基础数据矩阵共34个。对34个基础数据矩阵使用基于负荷轴的有序工况划分算法进行工况划分。以验证集的监测结果来确定α的取值,表2是α取不同值时,验证集上的FAR。
选取使得验证集FAR最小的作为α的值,综合确定α=1.3较为合适。α=1.3时,工况划分结果如图2所示。
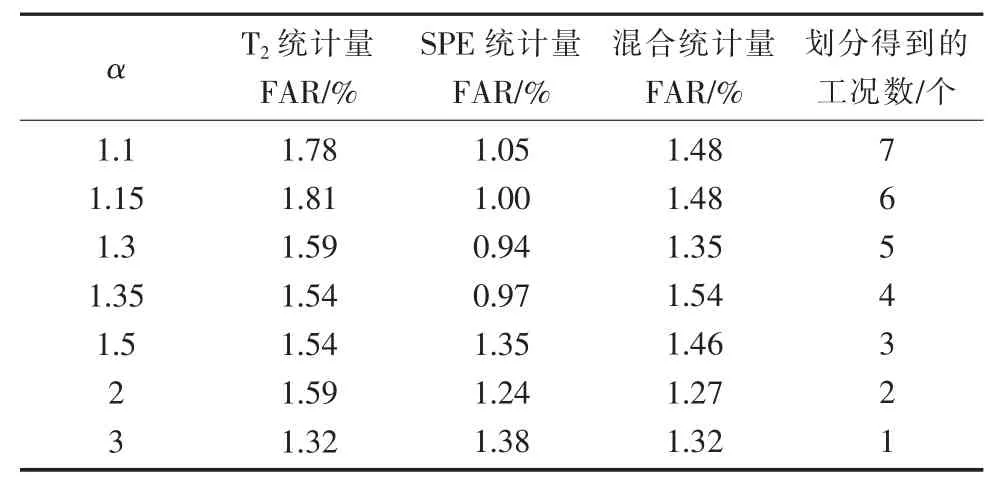
表2 不同α取值时统计量的FAR及划分得到的工况数1
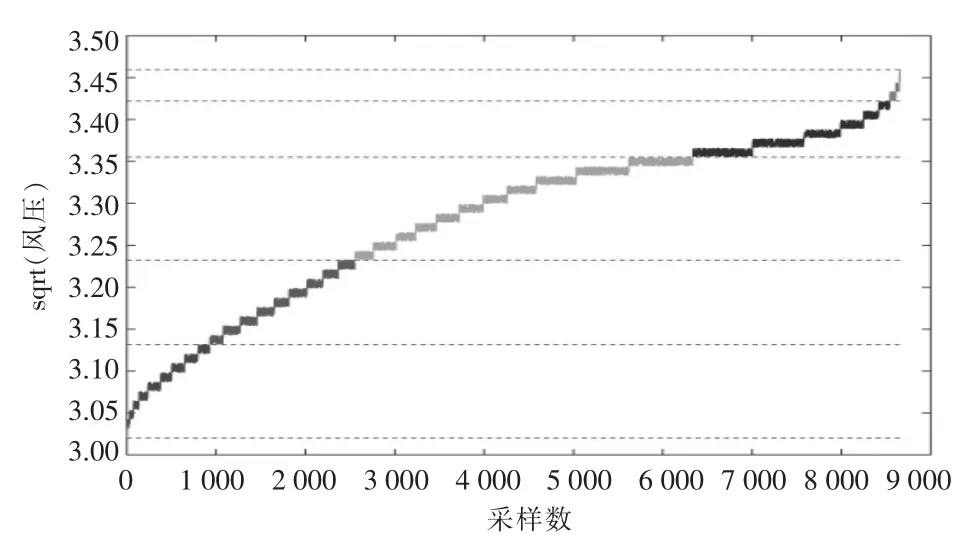
图2 工况划分结果
至此,得到了划分出的5个工况。根据工况划分结果,在每个工况内,分别建立1个PCA监测模型,最终得到5个子模型。
2.3 监测结果
建模完成后,在正常测试集1,Xtest1(900×36)上进行监测,查看监测效果。对处在不同工况区间内的样本调用不同的监测模型,最终得到的监测结果如图3所示。
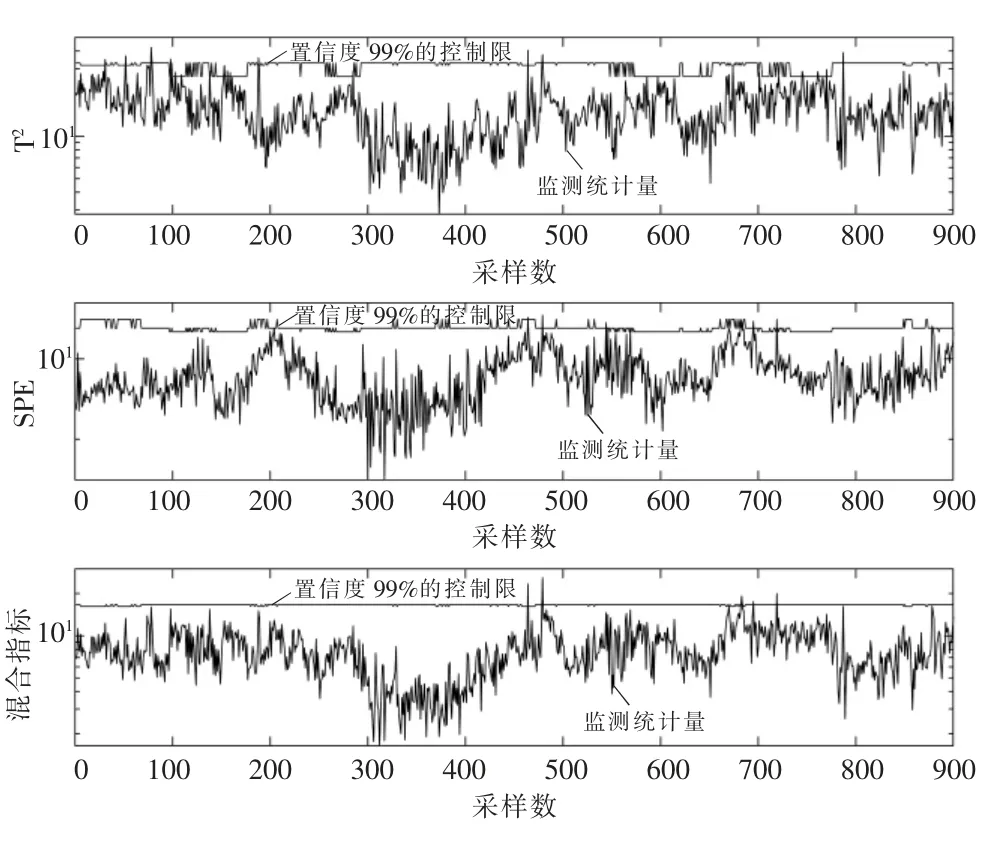
图3 测试集1监测结果
由图3可知,无论是T2,SPE还是两者的混合指标,只在个别样本点处略微超出控制限,且超限时间很短,不存在较长时间连续超限的现象。经统计,在T2,SPE以及两者的混合指标下,FAR分别为0.022 2,0.010 0和0.006 7。
在异常测试集2,Xtest2(500×35)上进行监测,查看监测效果。对不同工况下的样本应用不同的监测模型,最终得到的监测结果如图4所示。
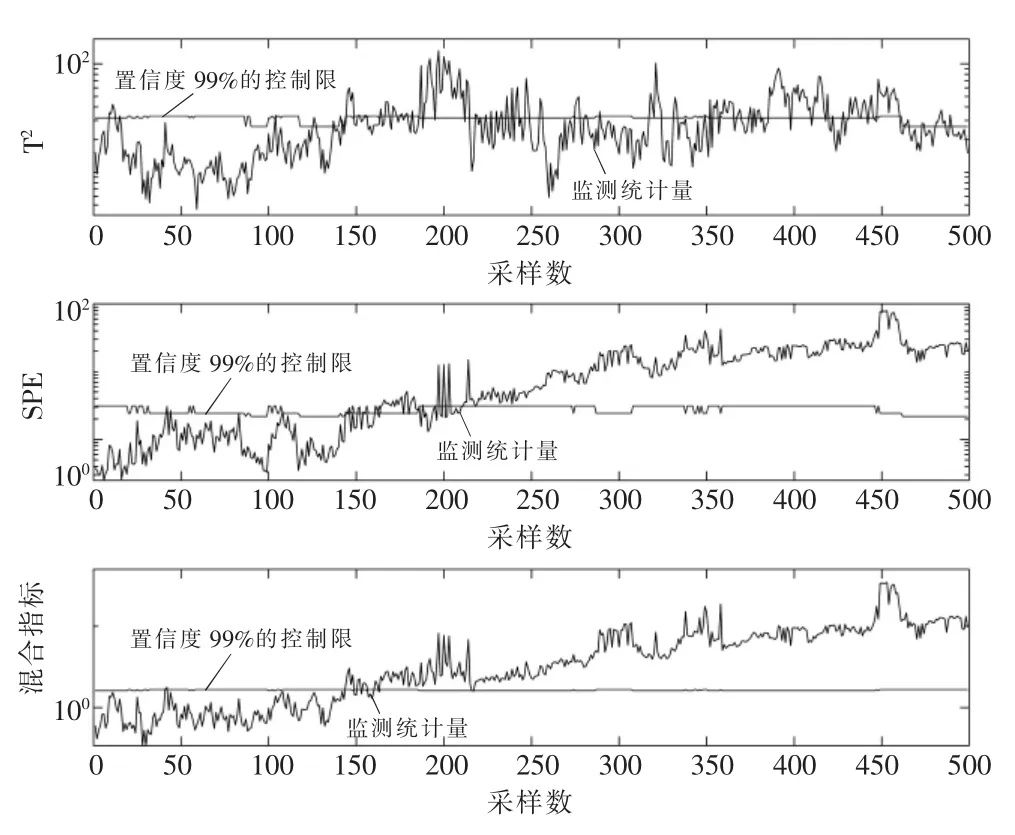
图4 测试集2监测结果
由图4可知,从第144个样本点开始,混合指标超出控制限,意味着检测到了故障,相比故障真正的发生时间延后44个样本点(132 min)。
为验证本文所提方法的有效性,与以下2种方法进行对比:第一种方法是使用高斯混合模型聚类后在各个类内使用PCA进行监测;第二种方法是不进行工况划分,将全部标准化后的负荷片合并后使用PCA进行监测。以正常测试集的FAR和异常测试集的检测时延作为评价指标,结果如表3所示。由结果可知,本文所提方法相对于基于一般聚类算法的监测方法,在保证较低FAR的同时,检测时延显著减少,能够更加灵敏地检测出故障。同时,与第二种方法的对比可以说明进行工况划分的必要性。
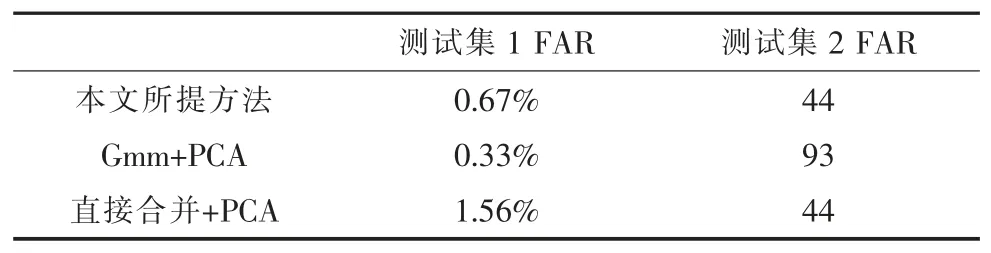
表3 3种方法结果比较
3 结语
本文针对火电热力系统关键设备的非平稳状态监测问题提出了一种基于负荷轴工况划分方法的监测策略。相比于基于协整分析的非平稳过程状态监测方法,该方法解决了不存在协整关系的非平稳变量的监测问题。相比于传统的以聚类为基础的工况划分方法,提出的方法考虑了同一工况下负荷相近、运行特性相似的特点,将时间轴转为负荷轴,构造了负荷片,并以监测模型的性能优劣来指示工况划分,更具有合理性。在每个划分出的工况内,可认为过程是平稳的,建立了主元分析模型来进行监测,从而实现了对非平稳过程的状态监测。利用浙江某发电厂一次风机实际的运行数据,验证了这种方法的可行性和有效性。该方法还可以扩展和推广到火电热力系统其他设备,乃至其他非平稳过程中。
