掌握解题规律,提升核心素养*
——以解决多元最值问题为例
2020-01-10江苏省西亭高级中学226300瞿春波
江苏省西亭高级中学 (226300) 瞿春波
近年来在各级各类考试中经常出现求解多元最值问题,这些问题字母多、式子繁、涉及知识面广、技巧性强,很多学生解答时思维受阻,导致得分率较低.笔者根据自身的教学实践和方法积累,同时以2019模拟试题为例,介绍解决此类问题的10种优化策略,供读者参考.
1.利用基本不等式
利用基本不等式求最值,关键在于“拆、拼、凑”,将条件式或待求式变形为“和或积”为定值.常见的变形技巧有转化符号、拆补项、配凑系数等.
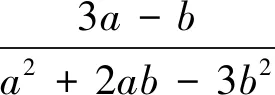
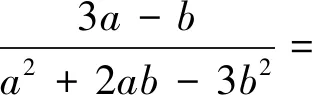
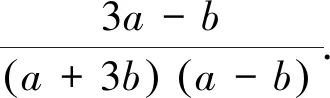
点评:抓住待求式中分母可以分解为一次因式乘积的特征,对分母实施双换元,再利用“1”代换.当然,此题还可以通过消元,转化为一元函数解决.
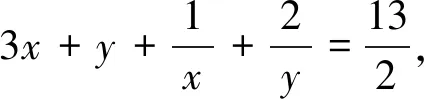

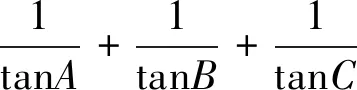
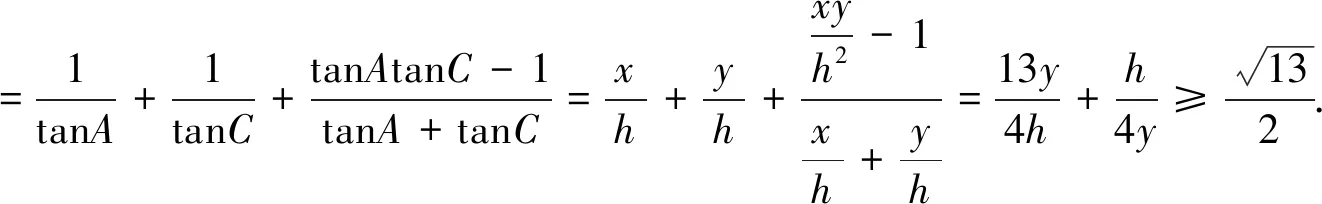
点评:三角形与不等式交汇问题是近几年高考及模考常见题型,具有江苏卷特色,此类题的破解策略大致有转化为边、转化为角、建系等几种.
2.代入消元
若各变量之间存在某种关系,则将其中的某个变量用其余的变量线性表示,代入目标式,从而化为一元(单变量)函数,再求最值.
例2 (2019南通名师高考原创卷(二))已知正数x,y满足xy(x+2y)=2,则x+y的最小值为.
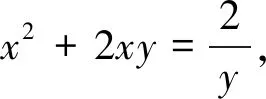
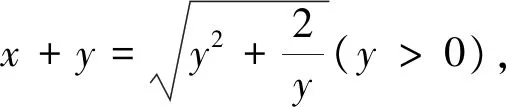
变式(2019南师附中高三上期中)已知实数x,y,z∈[0,4],若x2,y2,z2,是公差为2的等差,则
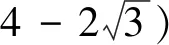
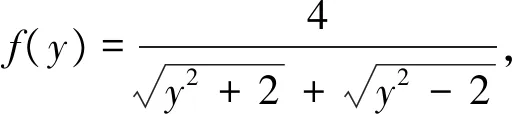
3.整体换元
若已知(或待求)因式之间具有某种关系,则引入一个(或几个)新的变量,替换掉原先某些因式.常见的换元方法有比(倍)值换元、差值(增量)换元、单换元、双换元等.
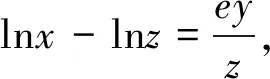
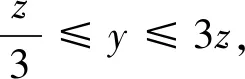
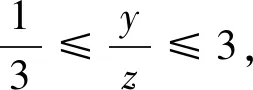
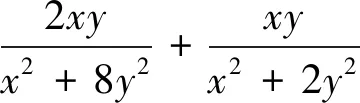
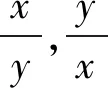
4.三角代换
若条件式(或待求式)明显反映出三角函数式特征,则以三角函数为“元”,将原问题转化为三角问题,从而利用三角公式及三角函数性质解决.
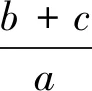
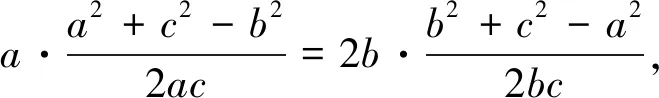
点评:将切化为弦,利用正余弦定理,再将角化为边,经过变形,得到两个变量的平方和为“1”,于是三角换元(引入角参),从而转化为三角问题.
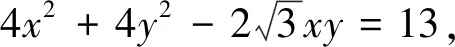
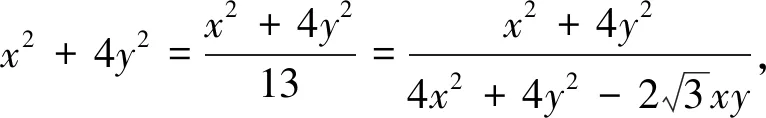
5.判别式法
若条件式(或目标式)经过恒等变形后可以整理为关于某个变量的一元二次方程,则利用“一元二次方程根的分布”求解参数范围.
例5 (2019江苏海门期中)设a,b是两个正数,且a2b+3ab2=a-b,则b的最大值为.
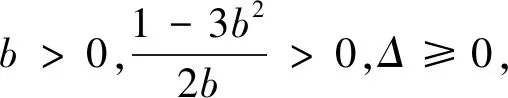
点评:不难发现,此题条件为二元二次方程且“目标”是求参数b,于是将原方程看成关于a的一元二次方程,利用方程有正根解决.
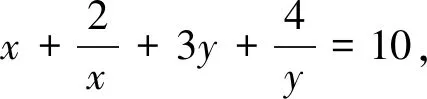
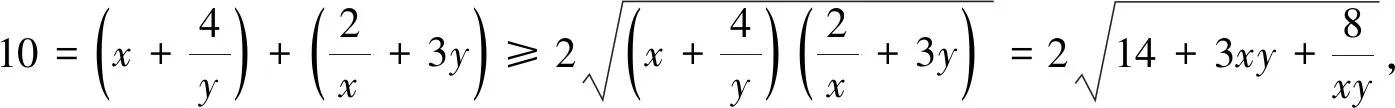
6.数形结合
若条件式或待求式具有某种几何意义,则往往数形结合,如此处理直观明了,化难为易.
例6 (2019苏北四市高三下学期初模拟)
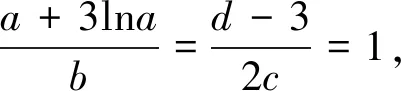
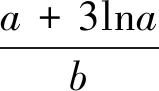
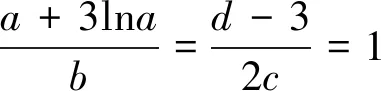
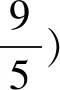
点评:此题难度不大,但得分率不高,与学生交流后,找到错因:(1)漏掉可行域中的一个对称区域;(2)错误认为待求式表示原点与可行域中“顶点”的距离平方.
7.多元配方
若条件式(或目标式)的结构中蕴含二次关系时,则优先考虑配方法[1].
例7 (2019浙江名校协作体联考)若正数a,b,c满足a2+b2+c2-ab-bc=1,则c的最大值为.
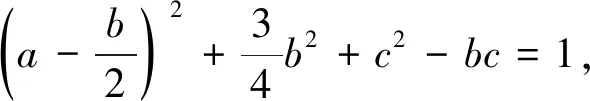
点评:以a为主元,配方;再以b为主元,再配方,利用平方的非负性,构造关于c的不等式.此题还可以将原等式先后转化为关于a和b的一元二次方程,利用根的分布(两次)解决.
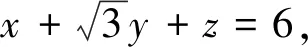
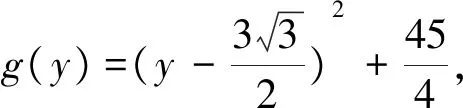
8.转化主元
如果某个表达式中含有多个变量且无法消元时,可以将其中某个变量看成主元,其余变量看成常量逐步处理[2].
例8 (2019届杭州高三上联考)已知函数f(x)=lnx-ax-b对任意的a<0,b∈R都存在x0∈[1,m],使得|f(x0)|≥1成立,则实数m的取值范围为.
解析:由|lnx0-ax0-b|≥1,得b≤-x0a+(lnx0-1),b≥-x0a+(lnx0+1),将其看成关于a,b的二元一次不等式,则约束条件为
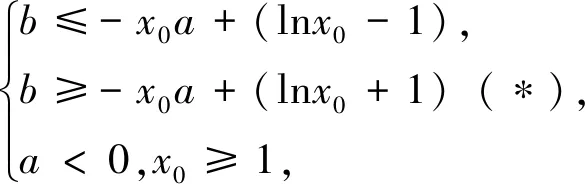
点评:此题利用绝对值性质去掉绝对值,通过转换主元(将a,b看成主元,x0看成参数)机智的避开繁琐的分类讨论,转化为线性规划解决.
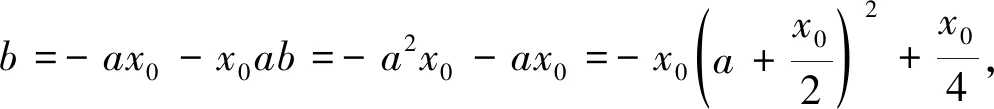
9.待定系数法
将目标式用条件式结合必要的待定系数表示出来,再进行“技术”处理求出待定系数,将问题转化为研究新表达式的相关指标[1].
例8 (2019浙江宁波模拟)已知实数x,y满足6x2+4y2+6xy=1,则x2-y2的最大值是.

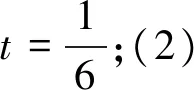
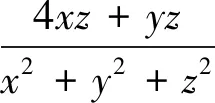
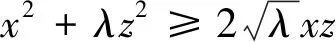
10.构造向量
向量是沟通代数和几何的重要桥梁,也是解决非向量问题的“隐藏”工具,巧妙运用向量性质解题可以使思路“豁然开朗”.
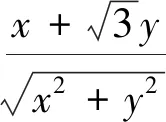
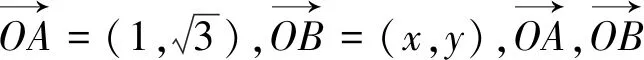
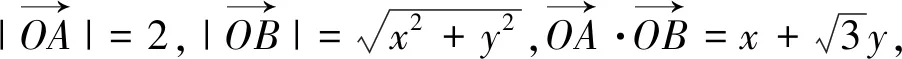
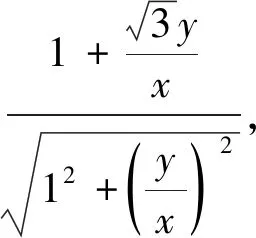
变式(2019江苏如东高三期末)已知实数x,y满足x2+y2≤1,则|2x+y-4|+|6-x-3y|的最小值为.(答案:5)
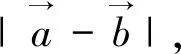
|3x+4y-10|=-(3x+4y)+10≥5.此题还可以根据条件中可行域,去掉待求式中两个绝对值,转化为线性规划问题,但计算繁琐,用时太多.
思维决定“行为”,思路决定“出路”,纵观上述破解多元最值问题的10种策略(尤其是策略8,9,10),背景新颖、交汇性强、题型多变、策略多样,贯穿多个知识模块,渗透多种数学思想方法.这就需要解题时深挖隐含条件、细心观察条件式及目标式结构特征,从而找到解决此类问题的最佳路径.
