基于模糊集合理论的中医诊断规则实现

蒋杰聘 吴敏 徐瑾 谢徐锦 吴哲辉

1.嘉兴学院商学院；2.嘉兴市中医医院

中医证型诊断很多都是经验规则，而模糊系统往往是用基于人的经验的语言规则来描述，经过模糊推理实现系统的。

一、模糊集合在中医诊断系统规则库中的相关定义

定义1[2]模糊集：集合X上的模糊集合是一个映射A：X→[0,1]，A也称为模糊集合X的隶属函数，常记为μA.对x∈X，A(x)称为X属于模糊集A的隶属度。

定义2[2]用F(X) 表示X上模糊集合的全体，即F(X)={A|A:X→[0,1]}。

定义3[2]设A，B∈F(X),A与B的并A∪B，交AB，补Ac的隶属函数定义为：

模糊逻辑推理是建立在模糊逻辑基础上的不确定性推理方法，是在二值逻辑三段论基础上发展起来的。这种推理方法以模糊命题为前提，动用模糊产生式规则，推导出一个近似的模糊结论。

定义4[1]模糊命题：含有模糊概念、模糊数据的语句称为模糊命题. 它的一般表示形式为：

X is A 或者 X is A(CF)

其中：A是模糊概念，用模糊集及隶属函数刻画；X是论域上的变量，用以代表所论述对象的属性；CF 是模糊命题的可信度。

定义5[1]模糊产生式规则的一般形式是：E→H(CF,λ) 其中，E是用模糊命题表示的模糊条件；H是用模糊命题表示的模糊结论；CF∈[0,1]是前提的隶属度，表示前提的可信度；λ∈[0,1]是推理的隶属度，表示该推理的可信程度。

定义6[3]:中医诊断系统规则库是一个四元组，M=(P,G,P0,f)其中：

(1)向量P=(P1,P2,…,Pm)存储记录m个决策属性及其论域。

(2)向量G=(G1,G2,…,Gn)存储记录划分的n个属性等级。对每个属性信息Pi∈P，划分等级数不大于n。

(3)向量P0=(P01,P02,…,P0m)存储记录m个属性的当前信息。

(4)决策属性隶属度函数f为映射P×G→(0,1)，定义了不同决策属性值对各属性等级的隶属度。一般由领域专家给出，或基于大量实践数据统计获得。

二、模糊推理规则实现

现将上述定义进行理论上的实践，应用在中医诊断中，选取血压和脉搏作为决策属性，定义模糊集的输入输出隶属度函数，并且建立模糊推理规则。

（一）数据模糊化

借用工具，测出血压P1∈(0,140]，测出脉搏P2∈(0,100],根据中医诊断的经验，可将血压高低程度分成血压偏低，血压正常，血压偏高，并将其涵盖于 x 的论域（0，140]，其隶属度函数如图2给出了血压高低（0，140]对血压偏低，血压正常，血压偏高3个等级的隶属度的一种定义，同理，可将脉搏高低程度分成脉搏偏低，脉搏正常，脉搏偏高，并将其涵盖于 x 的论域（0，100]，其隶属度函数如图3给出了血压高低（0，100]对脉搏偏低，脉搏正常，脉搏偏高3个等级的隶属度的一种定义。

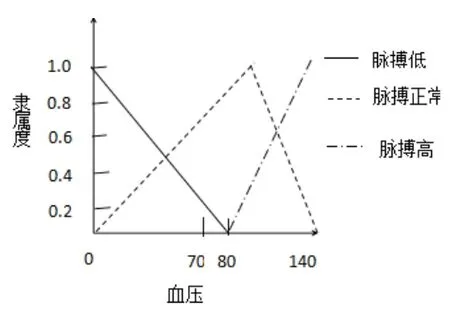
图2 血压高低对各等级的隶属度曲线

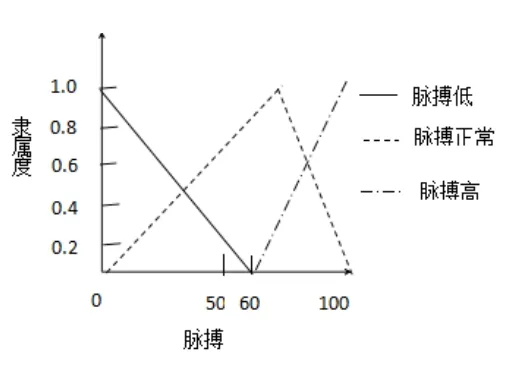
图3 脉搏高低对各等级的隶属度曲线

（二）建立推理规则库

推理症状被划分为气血亏虚、情绪压力、低血压、高血压、正常、窦性心动过缓6个等级，表1定义了一种不同血压等级和脉搏等级组合下症状等级的分明推理规则。

表1 模糊合成推理规则库

根据图2，当血压为110时隶属度为：

同理，根据图3，当脉搏为40时隶属度为：

由于血压（110）对血压低，脉搏（40）对脉搏高的隶属度为0；所以表1规则库中的血压低行和脉搏高列不被激活. 激活规则如表2所列。

表2 被激活规则表

（三）模糊合成

由表2知有如下4条规则被激活：

(1)血压正常∧脉搏低→窦性心动过缓；

(2)血压正常∧脉搏正常→正常；

(3)血压高∧脉搏低→窦性心动过缓；

(4)血压高∧脉搏正常→高血压；

由于以上规则中连接两个条件的是“且”，故在此选用取最小值法确定四条规则的强度：

规则1：血压对血压正常隶属度为0.70,脉搏对脉搏低隶属度为0.40，min（0.70，0.40）=0.40；

规则2：血压对血压正常隶属度为0.70,脉搏对脉搏正常隶属度为0.60,min（0.70，0.60)=0.60；

规则3：血压对血压高隶属度为0.30，脉搏对脉搏低隶属度为0.40，min（0.30，0.40）=0.30；

规则4：血压对血压高隶属度为0.30，脉搏对脉搏正常隶属度为0.60，min（0.30，0.60）=0.30；

规则1和规则3的结论都是窦性心动过缓，根据容斥原理，所以隶属度为0.4+0.3-0.4x0.3=0.58。

而规则2结论是正常的隶属度为0.6，规则3结论是高血压的隶属度为0.3。

综上所述，此样例结论应该为正常。

三、总结

模糊集理论能够较好地将中医诊断中的经验定量出来，正确地确定隶属函数是运用模糊集合理论解决实际问题的基础。隶属函数的确定过程，本质上说是客观的，但每个人对于同一个模糊概念理解又有差异，因此，隶属函数的确定又带有主观性。所以本文应用模糊集合理论构建中医证型判断的规则库，从而构建一个简便的中医智能诊断平台。