舵面形状对铰链力矩的影响分析
2020-01-10罗浩浩陈少松
罗浩浩,陈少松
(南京理工大学 能源与动力工程学院,江苏 南京 210094)
制导弹箭能迅速地改变飞行速度大小与方向的能力称为导弹的机动性,导弹机动性主要是通过控制弹箭的操纵面来实现。弹箭操纵时,操纵面偏转某一角度,在操纵面上产生空气动力,该空气动力相对于操纵面转轴(即铰链轴)的力矩,称之为铰链力矩。舵面铰链力矩的大小,直接影响制导弹箭的机动性。铰链力矩越大,在一定舵机功率下得到的舵偏转速度越小,飞行时弹箭对控制指令的响应越缓慢。铰链力矩系数取决于舵的类型、舵面几何形状、舵轴位置、马赫数、攻角和舵偏角,在弹箭设计过程中,为尽量减小铰链力矩,常采用轴式气动补偿,即将舵轴移至压心附近。然而,随飞行马赫数在亚跨超范围内变化,舵面压心在一个较大范围内移动,超音速段压心后移,亚跨音速段压心前移,对于全速域飞行弹箭,轴式补偿并不能很好地兼顾。因此,本文主要研究舵面形状对压心的影响,希望通过改变舵翼平面几何形状,缩小舵面压心在亚跨超音速内的移动范围,从而有利于进行轴式补偿,减小铰链力矩。
对于三维舵翼,舵面流动既有弦向分速,也有展向分速。在大攻角下,舵面流动还存在边界层分离现象,导致气动载荷(压强差)在舵面上不同位置的分布是不同的,有些位置载荷比较大,有些位置载荷比较小,这些载荷对铰链轴的积分得到铰链力矩,如果能够将这些载荷的分布摸清,截去对铰链力矩不利的部分舵面,就能够改变舵面压心的位置,从而改变铰链力矩。舵面载荷的分布规律除与舵面形状有关外,还与速度等有关,因此需要对有关舵面在所关心的速域范围进行细致研究。
目前,国内外有许多学者针对铰链力矩的影响因素做了研究。李斌[1]、欧平[2]等人通过CFD模拟软件,研究了制导弹箭舵面与弹体表面之间的缝隙效应。TANG[3]对HL-10升力模型进行测试,分别研究了舵面偏转角、迎角、侧滑角和马赫数变化对舵面铰链力矩的影响,结果表明,马赫数的影响在亚跨音速段较明显,超音速段压心变化不大。对于舵翼平面几何外形对铰链力矩的影响,LESIEUTRE[4]进行过类似研究,并且开发了一款软件用于优化弹翼平面形状以最小化舵面铰链力矩,但其对舵翼平面的优化仅限于后缘曲线的变化,对于通过裁剪舵翼调整压心的研究尚不明确。
通过风洞实验研究舵面形状的变化对弹箭气动特性的影响成本较高,并且随着计算机技术的发展,CFD技术逐渐发展成为空气动力学研究的有力手段。因此,本文主要运用CFD软件对某无翼式布局火箭弹进行数值模拟,分析尾舵的受力分布。通过裁剪尾舵的不同部位,得到不同形状的尾舵,形成多组弹身-尾舵组合体,对各组合体进行数值模拟计算,研究各组合体的舵面弦向压心分布情况、舵面铰链力矩的变化规律以及全弹的气动特性,为减小制导弹箭的舵面铰链力矩,提高弹箭的机动性与控制精度提供了一定的帮助。
1 数值计算方法
1.1 控制方程与湍流模型
控制方程采用三维积分形式的雷诺平均N-S方程[5]:
式中:t为时间,S为面积,V为任意控制体,W为守恒变量,F为无粘通矢量项,FV为粘性通量,∂V为控制体边界,n为控制体边界单位外法向矢量,Re为雷诺数。
针对飞机铰链力矩的预测,迟永一[6]对各湍流模型与离散格式计算飞机铰链力矩做了比较,结果表明,Spalart-Allmara湍流模型的计算效果更好,数值计算结果精度随离散格式阶数提高而提高。故本文各模型计算均选用S-A单方程湍流模型,离散格式flow项与Turbulence项均采用二阶迎风格式。
1.2 计算模型与网格划分
本文原始计算模型采用无翼式弹箭布局,弹径为D,弹长L=7.13D,4片后掠尾翼根弦长D,展长3D,前缘后掠35°,后缘后掠5.7°,呈“×”形布局,舵偏角均为-20°,呈俯仰状态,铰链轴轴向位置位于距弹箭顶点6.67D处,模型代号CB,各尾舵从弹体头部看逆时针依次编号为舵1、舵2、舵3、舵4。全弹模型如图1所示。模拟工况攻角α=4°,马赫数变化范围为0.6~4.5。

图1 计算模型CB
采用ANSYS ICEM软件对计算模型划分结构化网格,考虑到计算工况的马赫数变化范围包含亚、跨、超音速,计算域前场约为6倍弹长,后场约为7.5倍弹长,径向取25倍弹径,图2为CB模型计算网格示意图。

图2 CB模型计算网格简图
1.3 收敛性验证
本文在CB模型基础上划分了3套网格,网格数量分别为260万、400万、500万。计算来流马赫数2.5,攻角α=0°工况下舵4的压心系数与铰链力矩系数,以便进行网格数量收敛性验证。计算结果如表1所示。表中,N为网格数量;Xcp为舵面压心系数;mh为舵面铰链力矩系数;ΔXcp为压心系数的相对误差;Δmh为铰链力矩系数的相对误差,ΔXcp和Δmh是由260万、400万网格数量的计算结果分别与500万网格数量的计算结果相比得到。从表中可以看出,当网格数量达到400万时,最大差值仅为1.5%,故本文采用400万网格数量。其中本文各舵面气动特性以模型CB的尾舵根弦前缘点坐标为参考点,根弦长为参考长度Lref,舵面面积为参考面积Sref。

表1 网格收敛性验证
1.4 准确性分析
为了验证数值模拟方法的准确性,本文计算了验证模型在马赫数Ma=1.6时,迎风舵舵4的铰链力矩系数随攻角的变化曲线,并与文献[7]中给出的铰链力矩系数曲线进行对比。模型与数值均取自文献[7],弹长L1=1 023.4 mm,弹径D1=76.2 mm,铰链轴距顶点921.7 mm,尾舵翼展为4D1,根弦长1.5D1,前缘后掠60°,4片尾舵呈“×”形布局,舵偏角0°,参考长度114.3 mm,参考面积4 560.4 mm2,模型尺寸和计算结果对比曲线见图3。从图中可以看出,在小攻角下,铰链力矩系数大致呈线性变化,此时CFD计算结果与文献值吻合度较高,当攻角继续增大,数值计算结果与文献值大致趋势一致,此时最大误差为10%,本文误差均为相对误差。

图3 验证模型与舵4铰链力矩系数随攻角的变化曲线
2 舵面受力分析
图4为Ma=2.5,α=4°时舵4背风面与迎风面压力云图。从图中可以看出,在超音速状态下,尾舵的背风面压力梯度不大,迎风面从前缘往后缘,梢弦往根弦所受压力递减,所以尾舵受力主要集中于右上角三角形区域。图中,A—A截面和B—B截面分别位于距前缘和后缘0.03D处,提取截面处舵4迎风面与背风面的压力差,如图5所示,图5中η为尾舵展向比例。从A—A截面看出,上下翼面压差形成的载荷在亚跨音速下主要集中在翼面的中间部分,在马赫数大于1.5后,载荷沿展向递增,但接近梢弦时又急剧下降,对于无限长直弹翼,弹翼任何一个翼剖面的绕流都是一样的,此时弹翼上下表面压强所产生的升力是一样的。但实际弹翼展向长度并不是无限延伸的,在翼尖部位,此时弹翼下方的高压空气会在梢弦处向上方的低压空气翻过去,翼尖涡由此产生,其结果导致上下表面压强在翼尖部位趋于一致,舵面载荷曲线急剧下降。从B—B截面看出,在亚跨音速下,载荷沿展向的变化很小,当来流马赫数大于2.5以后,载荷沿展向急剧增加。
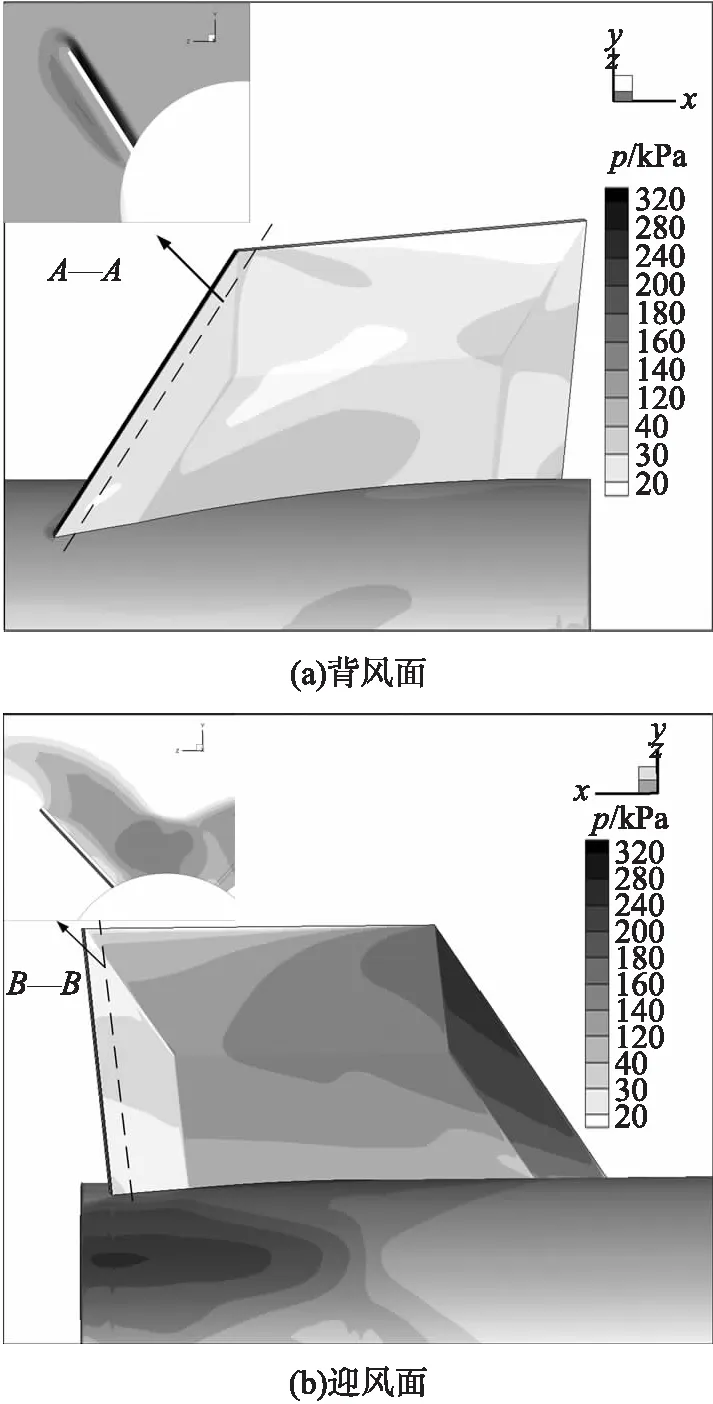
图4 Ma=2.5,α=4°时舵4压力云图
舵面前后缘距离舵轴较远,调节压心比较有利。从舵面载荷的分布规律可以看出,舵面前缘所受到的载荷大于后缘,对前缘裁剪可以有效地将压心向后调整,这样会增加压心的移动距离,然而同时对前缘梢弦的裁剪会很大程度削减其产生法向气动力的能力,增大尾舵前缘厚度从而增大阻力,所以本文对于前缘仅在根弦位置进行裁剪。而对于后缘附近裁剪似乎比在梢弦附近更为合理,亚跨音速下由于此处载荷小,压心向前调整的量不会大,而马赫数大于2.5后,此处载荷比较大,压心向前的调整必然较大,这样在亚跨超音速范围,使得压心的变化范围减小了,有利于在亚跨超音速下进行轴式补偿,都可以得到较小的铰链力矩。而对于根弦位置,其载荷较小,对舵面整体气动特性的影响可能不大,故本文同时也对后缘根弦处进行裁剪,以作对比。
根据以上分析,本文对该弹箭尾舵做了如图6所示处理,组成3组弹身-尾舵组合体,其中CB1裁剪部位为0.12Lref处,CB2与CB3裁剪大小为0.075Lref×0.124Lref,三者裁剪面积保持一致0.022 5Sref,分别对各组合体进行数值模拟,研究尾舵平面几何形状对舵面弦向压心与铰链力矩的影响。

图5 舵4 A—A与B—B截面迎风面与背风面压差

图6 裁剪尾舵模型与网格划分示意图
3 气动特性分析
3.1 舵面气动特性
图7为攻角α=4°时舵4的舵面法向力系数CN随马赫数的变化曲线图。从图中可以看出,在亚跨音速阶段,裁剪尾舵对舵面的法向力有影响,当Ma=0.9,此时影响最大,其中模型CB1的舵面法向力系数相比模型CB相差4%,模型CB2与CB3相比模型CB相差3.33%。在超音速段,随着来流速度的增大,其舵面的法向力系数CN逐渐减小,裁剪尾舵对舵面法向力系数的影响也减小,当Ma=2.5,模型CB1相比模型CB,其舵面法向力系数相差2.4%,而模型CB2、CB3相比模型CB不超过2%。从前面的分析可知,如图4,尾舵在超音速段,其受力主要向尾舵前缘梢弦部位集中,裁剪部分面积小且所受压力不大,所以对尾舵的小面积裁剪并不会影响尾舵的升力特性。

图7 舵4舵面法向力系数随马赫数的变化曲线
图8为舵4的舵面弦向压心系数Xcp随马赫数的变化曲线,图9为α=4°时各模型舵4舵面压心在Ma=0.6~4.5下的分布图,压心系数以模型CB的尾舵根弦前缘点坐标为参考点,弦向压心系数以模型CB根弦长为参考长度Lref,图9纵坐标Ycp为展向压心系数,Ycp以模型CB舵面展长为参考长度。裁剪尾舵改变了尾舵表面压力分布,一定程度上影响了舵面压心分布。在亚音速段,压心的移动不明显,其中模型CB2与CB3的压心系数相比模型CB不超过1%。在超音速段,压心位移明显大于跨音速段,在Ma=3.5时模型CB2与CB3移动量达到最大1.5%,弦向压心前移,压心位置变化范围更加集中,如图9,其中模型CB在攻角α=4°姿态下,Ma=0.6~4.5的速域范围内弦向压心变化范围为0.389~0.529,而模型CB2与CB3弦向压心变化范围分别为0.385~0.521,0.387~0.520,其移动范围分别压缩了0.004和0.007,对铰链轴的设计更有利;而CB1模型,压心位移更大,当Ma>1.5时,其压心移动量均大于2%,但压心后移,整体压心变化范围将会更广。所以,当弹箭的飞行速度为亚跨超音速时,就舵面铰链轴的设计而言,对尾舵后缘部分的裁剪更有利于减小铰链力矩,对前缘位置的裁剪虽能更大程度上改变压心位置,但不利于铰链轴的设计。

图8 舵4舵面弦向压心系数随马赫数的变化曲线

图9 α=4°时舵4舵面压心在Ma=0.6~4.5下的分布图
图10为舵4舵面铰链力矩系数mh随马赫数变化曲线。从图中看出,3种模型的铰链力矩系数与舵面法向力系数同号,说明压心都在铰链轴的前面。对比图8舵面弦向压心系数随马赫数的变化曲线可以看出,两图中各曲线走势基本一致,说明裁剪尾舵能够改变尾舵的舵面铰链力矩,其主要是通过改变舵面弦向压心位置,进而改变舵面铰链力矩。在亚跨音速段,裁剪尾舵对弦向压心与铰链力矩的影响相比超音速段要小。当Ma=0.9时,相比模型CB,模型CB2与CB3的铰链力矩系数增大了10%;而当Ma=4.5时,模型CB1、CB2与CB3相比模型CB的铰链力矩系数差值均大于20%。
图11为舵4弯矩系数M随马赫数的变化曲线,该弯矩系数是对尾舵根弦取矩。可以看出,对尾舵裁剪后该曲线与图7舵面法向力系数一致。在亚跨音速段,当Ma=0.9时,模型CB2与CB3的弯矩系数相比模型CB变化最大,相差3.6%。在超音速段,当Ma>2.5时,随马赫数增大,裁剪后的模型相比模型CB差值逐渐变小,并且模型CB2的变化大于模型CB1与CB3,最大差值达3.5%;模型CB1的弯矩系数变化最小,与模型CB的最大差值仅为1%。但在弹箭的设计过程中,弯矩小幅度的变化可以通过其他工艺手段解决。

图10 舵4舵面铰链力矩系数随马赫数的变化曲线

图11 舵4舵面弯矩系数随马赫数的变化曲线
3.2 全弹气动特性
图12~图14分别为火箭弹全弹阻力系CD、升力系数CL与俯仰力矩系数mz随马赫数的变化曲线。以模型CB的全弹长L为参考长度,弹体最大截面积Smax为参考面积,俯仰力矩系数是对弹体顶点取矩。从图中可以看出,裁剪后的各弹身-尾舵组合体相比原始模型CB,差距不是很大。其中阻力系数在Ma=0.9时差值最大,模型CB2相比模型CB减小6%。在超音速段,裁剪后的舵面模型相比模型CB的阻力系数略有增大,其中模型CB1的增量大于模型CB2和CB3,在Ma>1.5时,模型CB1的增量达到1.5%,模型CB2和CB3相比模型CB差值仅在0.3%左右。模型CB1的裁剪方式会使尾舵前缘变钝,受力面积增大,前缘后掠角变小,从而使激波倾角增大,导致弹箭阻力系数增大。对于升力系数CL与俯仰力矩系数mz,裁剪尾舵在超音速段的影响较大,并且随马赫数增大而增大。当Ma=4.5时,模型CB1相比模型CB,升力系数减小8.6%,俯仰力矩系数减小4.6%。模型CB2和CB3相比模型CB,升力系数减小3%,俯仰力矩系数减小2%。当Ma>1时,前缘受力大于后缘,对尾舵前缘的裁剪方式,尾舵表面损失的压力大于对尾舵后缘的裁剪方式。而对亚跨音速段影响较小,当Ma=1.0时,模型CB1与CB2的升力系数与俯仰力矩系数略增大0.2%。

图12 α=4°时阻力系数随马赫数的变化曲线

图13 α=4°时升力系数随马赫数的变化曲线
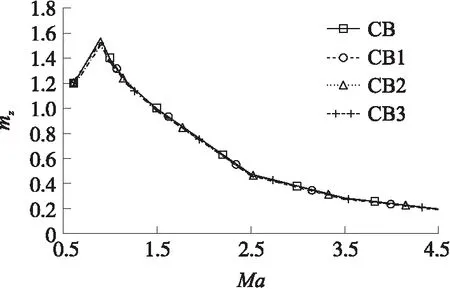
图14 α=4°时俯仰力矩系数随马赫数的变化曲线
制导弹箭的飞行性能与弹体的稳定性密切相关,图15为来流攻角α=4°且舵偏角δ=0°时压心系数Xcp随马赫数的变化曲线图,压心系数以弹体顶点为参考点。从图中看出,不管何种剪裁方式,弹箭的整体压心系数都有小幅度的改变。在亚跨音速段,当来流速度较低时,裁剪后的模型相比模型CB压心的改变量较小。当马赫数增大时,压心前移幅度逐渐增大,在Ma=3.5时,压心前移量最大,此时模型CB2与CB3相比模型CB压心前移0.38%,模型CB1的压心前移量稍大于模型CB2与CB3,达到0.53%。对于压心在弹箭质心后的制导弹箭,相对距离越远,所提供的恢复力矩越大,静稳定性就越大[8]。因此,裁剪尾舵会一定程度上减小制导弹箭的稳定性,裁剪尾舵前缘对制导弹箭稳定性的影响大于对尾舵后缘的裁剪。

图15 α=4°且δ=0°时压心系数随马赫数的变化曲线
4 结论
本文采用CFD计算软件,对某无翼式布局制导火箭弹进行了数值模拟,分析了该制导火箭弹在舵偏角δ=-20°且攻角α=4°时的舵面受力分布,对尾舵前后缘做出小面积的裁剪,从而改变尾舵平面几何形状,组成3组弹身-尾舵组合体,计算了各组合体的舵面法向力系数、舵面弦向压心系数、舵面铰链力矩系数与弯矩系数,以及全弹的气动系数与压心位置。分析了裁剪尾舵对制导弹箭舵面弦向压心、舵面铰链力矩以及全弹气动特性的影响。结果表明:
①小面积裁剪尾舵对舵面法向力影响不大,对舵面弦向压心有一定的影响,超音速状态下,压心变化幅度要大于亚跨音速。裁剪尾舵前缘会使舵面压心后移,压心范围将更分散;裁剪尾舵后缘会使舵面压心前移,压心范围更集中,更有利于铰链轴的设计。
②小面积裁剪尾舵前缘或后缘,可以有效改变舵面铰链力矩的大小。。
③小面积裁剪尾舵前缘或后缘,在亚跨音速段对弹箭的整体阻力系数、升力系数以及俯仰力矩系数有一定的影响。
④裁剪尾舵会使制导弹箭整体压心前移,并且随马赫数的增大,压心前移幅度越大,对弹箭的静稳定性有些影响。
