基于弹道精确测量的射表编拟方法研究

贾 波,张 平,赵志明,王 龙

(中国人民解放军63850部队,吉林 白城 137001)

射表是武器系统实施正确射击、确保较高命中率、形成强大战斗力的前提和条件,也是设计火控计算机、指挥仪等必需的基础数据。在射表编拟中,弹道建模、气动参数辨识、弹道符合计算以及数据优化处理是核心技术环节,制约着射表技术的提高和发展,而这些技术的提高又取决于弹道测试能力和水平的发展,纵观目前的射表编拟技术,存在以下突出的问题:

①射表试验耗弹量较大,试验周期较长。目前编一个单装药号射表需要消耗100多发弹。对于高精度和高智能化武器,每项试验的总消耗在几千万元以上。由于射表试验对气象条件等试验条件要求严格,巨大的射击试验量也导致射表试验周期较长。

②除阻力系数外,其他气动力参数误差较大。目前阻力系数是通过采用C-K法符合弹道径向速度辨识获取,精度比较高,而其他气动参数均通过流场模拟计算得到,误差很大,直接影响射表编拟精度,影响武器装备的射击效能和作战能力[1]。

③射表编拟方法滞后于测试技术发展,目前遥测、光测等技术发展迅猛,可以提供较为准确的全弹道诸元测试数据,但射表编拟没有充分挖掘和利用这些数据,射表编拟依然处于“打”射表而不是“编”射表的模式。

综上所述,开展“基于弹道精确测量的射表编拟方法研究”,综合运用雷测、光测、遥测等技术手段,基于弹箭全弹道坐标、速度、姿态及转速等飞行诸元精确测量结果,全面准确辨识弹箭气动参数及射表基础参数,全面符合弹道特征参数,最终形成基于弹道精确测量的射表编拟新方法,可从根本上解决射表编拟试验消耗大、试验周期长的问题,为射表编拟精度和技术水平的提高提供理论基础和技术支持。

本文从弹箭弹道建模出发,开展了气动参数和符合系数灵敏度分析计算,针对气动参数辨识和全弹道符合计算方法,进行了详细的理论推导和仿真研究,得到明确的研究结果,初步形成了基于弹道精确测量的射表编拟新方法。

1 弹箭飞行弹道模型

建立精确的弹道模型是开展研究的基础,本文采用弹箭六自由度刚体弹道方程,弹箭六自由度刚体弹道方程考虑了作用在弹箭上的所有力和力矩,与弹箭实际飞行状态吻合较好,计算精度高,满足弹道研究和射表计算需求。弹箭运动方程常用的坐标系有地面坐标系Oxyz、弹道坐标系O1x1y1z1、弹轴坐标系O1ξηζ和弹体坐标系O1x2y2z2,根据弹道理论,弹箭在地面坐标系Oxyz下的六自由度运动方程可用下列方程来描述[2]:

式中:m为弹丸质量,v为弹丸质心的飞行速度,θ和ψ为弹道倾角和弹道偏角;x,y和z为弹丸质心在坐标系Oxyz中的空间坐标;φa为弹箭的俯仰角;φ2为弹箭的偏航角;Fx1,Fy1和Fz1为作用在弹丸质心上的各种力在坐标系O1x1y1z13个轴上的投影分量;Mξ,Mη,Mζ为外力矩在坐标系O1ξηζ三个轴上的分量;ωξ,ωη,ωζ为弹轴转动角速度在坐标系O1ξηζ3轴上的分量,γ为弹箭旋转方位角,JC为弹箭的极转动惯量,JA为弹箭的赤道转动惯量,参量βDη和βDζ可表示为

βDη=βD1cosγ-βD2sinγ
βDζ=βD1sinγ+βD2cosγ

式中:βD1为惯性主纵轴在坐标系O1x2y2z2的O1x2y2平面投影与O1x2的夹角;βD2为惯性主纵轴与O1x2y2平面的夹角。

2 气动参数辨识方法

气动力参数是编拟射表和弹道研究不可缺少的基础参数。目前,阻力系数是通过采用C-K法利用弹道径向速度提取的,精度较高,而其他气动参数均通过流场模拟或经验公式计算得到,但由于受湍流模型和转捩位置不确定的影响,某些情况下数值模拟或经验公式的计算结果存在较大的误差,随着武器装备的发展和射表技术的进步,这些参数就成了制约射表精度提高的瓶颈。利用弹道测试数据辨识更为准确的气动力参数和其他弹道关键参数已经成为进一步提高射表精度的重要手段。

2.1 辨识准则及算法

常用参数辨识准则有最小二乘、最大似然、最小方差、最小风险、最小预报均方差等,在给定的辨识准则下,可将参数辨识问题转化为求某准则函数(即目标函数)的极值优化问题。辨识算法一般分为二类,即迭代算法和递推算法,常用迭代算法一般有牛顿法、梯度法、高斯法等。目前在系统参数辨识的众多准则和算法中,应用最为广泛的是最大似然准则和修正牛顿-拉夫逊算法[3-4]。

假设弹箭飞行过程中的过程噪声可忽略不计,则最大似然辨识准则可写成:

式中:i为观测量样本序号,i=1,2,…,N,N为观测量的样本总数,ν(i)为输出误差,表达式为

采用牛顿-拉夫逊迭代算法求解极值问题,具有效率高、收敛快的特点,是较为有效的迭代算法。对于上式所示极值问题,其迭代修正公式为

2.2 气动参数灵敏度分析

建立基于六自由度刚体弹道模型的灵敏度分析模型,针对弹箭气动参数进行仿真分析,可以摸清气动参数变化规律,有效识别对弹道特性影响最大的气动参数,为气动参数辨识方法的建立奠定基础。以某型155 mm杀爆弹为例,飞行诸元关于各气动参数的灵敏度曲线如图1～图6所示。t为飞行时间,S为各观测量关于待辨识参数的灵敏度。

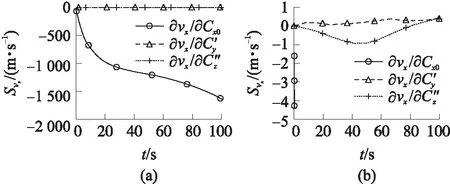
图1 vx关于待辨识参数的灵敏度

图2 vy关于待辨识参数的灵敏度

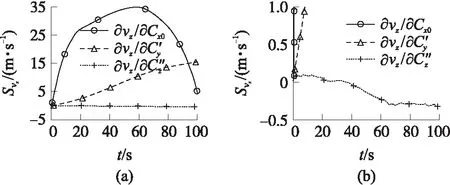
图3 vz关于待辨识参数的灵敏度

通过灵敏度分析,可以看出:

①榴弹飞行速度vx和vy对零阻系数Cx0最敏感,其次为马氏力系数导数C″z,再次为升力系数导数C′y,其他参数变化对vx和vy影响不大,可以忽略不计;飞行速度vz对零阻系数Cx0和升力系数导数C′y最敏感,其次为马氏力系数导数C″z,其他参数变化对vz影响不大,可以忽略不计;

③榴弹的俯仰角φa对马氏力矩系数导数m″y和翻转力矩系数导数m′z最敏感,再次为摆动阻尼力矩系数导数m′zd,其他参数变化对φa影响不大,可以忽略不计;偏航角φ2对翻转力矩系数导数m′z最敏感,其次为马氏力矩系数导数m″y,再次为摆动阻尼力矩系数导数m′zd,其他参数变化对φ2影响不大,可以忽略不计。

图4 γ′转速关于待辨识参数的灵敏度

图5 φa关于待辨识参数的灵敏度

图6 φ2关于待辨识参数的灵敏度

2.3 气动参数辨识仿真

同样以155 mm杀爆弹为例,以弹箭全弹道坐标、速度及姿态等飞行诸元的弹道仿真数据为观测值,待辨识参数为θ=(Cx0C′yC″zm′zm′xdm′zdm″y),采用流场模拟计算结果为初值。采用最大似然准则和修正牛顿-拉夫逊算法,辨识结果如图7～图13所示。

图7 零阻系数辨识结果

图8 升力系数导数辨识结果

图9 马氏力系数导数辨识结果

图10 翻转力矩系数导数辨识结果

图11 滚转阻尼力矩系数导数辨识结果

图12 摆动阻尼力矩系数导数辨识结果

图13 马氏力矩系数导数辨识结果

通过辨识结果图7～图13可以看出,采用飞行诸元为观测量,能够辨识出所有待辨识参数,精度较高,其中,马氏力系数导数C″z精度相对最低,辨识结果较为发散,这是由于所有观测量对这一参数都不太敏感所致。部分气动参数辨识结果在大马赫数时与真值相差较大,这与各气动参数敏感度在开始时较小有关,随着时间增加,马赫数减小,敏感度增加,同等条件下辨识结果会越来越接近真值。

图14为积分结果与观测量的对比,取偏差值K为

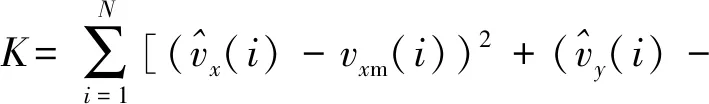
从图14可以看出,大马赫数时偏差较大,随着时间增加,马赫数减小,偏差也越来越小。总体来说,辨识结果较为准确,辨识方法可信。

该辨识方法同样适用于火箭弹气动参数辨识。能够辨识包含马格努斯系数在内的7个气动参数,辨识结果精度较高,辨识方法有效。

3 符合计算方法

符合计算是射表基础参数的精确化过程。符合系数及符合计算方法需依据弹箭的弹道特性及对射表的要求而确定,符合系数应是对符合对象影响的最大参量。目前,射表编拟中普遍采用的符合方法是以弹道终点诸元为符合对象,这仅能保证落点的准确,不能保证全弹道的准确,这也是当前射表精度差的主要因素之一,改进符合计算方法势在必行。对榴弹、火箭弹而言,计算所得弹道的最大弹道高Ymax、落点纵坐标X、落点横坐标Z以及飞行时间t与实际弹道相符时,就可以认为这两条弹道基本一致。因此,选取这4个弹道特征量为符合对象,研究确定符合系数及符合计算方法。

3.1 符合系数灵敏度分析

以155 mm杀爆弹为例,榴弹符合系数灵敏度计算结果如表1所示。表中,ΔYmax为最大弹道高改变量,ΔX为落点纵坐标改变量,ΔZ为落点横坐标改变量,Δt为飞行时间改变量。

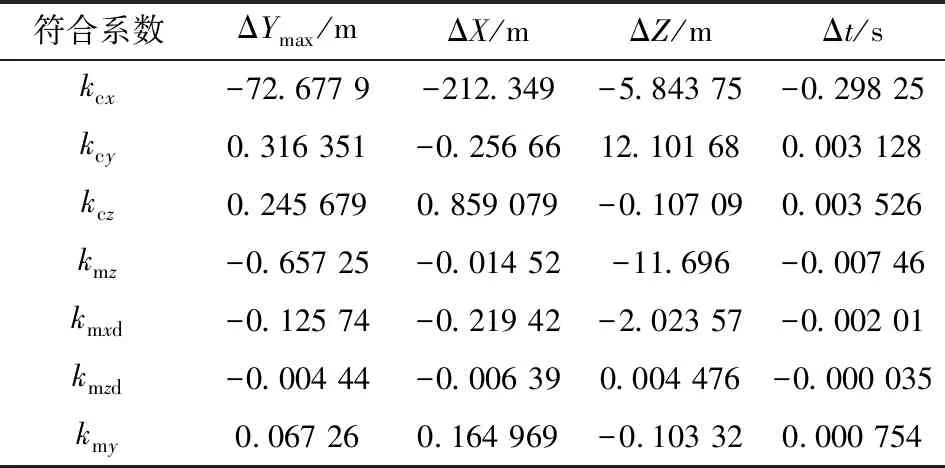
表1 榴弹符合系数灵敏度计算结果

通过分析,可以得到以下结论:对于榴弹,最大弹道高Ymax、落点纵坐标X对阻力符合系数kcx最敏感,落点横坐标Z对升力符合系数kcy最敏感,其次为翻转力矩符合系数kmz,两者灵敏度的绝对值相差不多;飞行时间t主要对阻力符合系数kcx比较敏感,所有符合对象对滚转阻尼力矩符合系数kmxd、摆动阻尼力矩符合系数kmzd和马氏力符合系数kmy均不太敏感。考虑到符合对象,榴弹可选取对弹道特征量影响较大的阻力符合系数kcx、翻转力矩符合系数kmz、升力符合系数kcy和马氏力符合系数kcz进行符合计算。

以122 mm火箭杀爆弹为例,火箭弹符合系数灵敏度计算结果如表2所示。通过分析,可以得出,对于火箭弹,最大弹道高Ymax、落点纵坐标X和飞行时间t对阻力符合系数kcx最敏感,其次为压心符合系数kxcp;落点横坐标Z对压心符合系数kxcp最敏感。考虑到符合对象,对于火箭弹的弹道符合,可以选取阻力符合系数kcx、压心符合系数kxcp、升力符合系数kcy和滚转符合系数kmxw来进行符合计算。

表2 火箭弹符合系数灵敏度计算结果

3.2 符合计算方法

对于榴弹,首先给定各符合系数初值,然后在实际条件下(初速、射角为实测值,实际气象条件和弹道条件等),将各符合系数代入弹道方程组中求解,当积分至y=Δy(炸高)时,若计算的落点纵坐标、横坐标、最大弹道高、飞行时间满足与实测值一致(符合精度0.01%),则符合计算结束,否则调整各符合系数重新计算弹道直至满足为止。

对于火箭弹,符合计算需在主动段和被动段分别进行。主动段选取推力符合系数kp、高低扰动符合系数kr1和横向扰动符合系数kr2,对终点最大速度vk、主动段终点倾角θk和偏角ψk进行符合计算;被动段选取阻力符合系数kcx、压心符合系数kxcp、升力符合系数kcy和滚转符合系数kmxw对落点纵坐标、横坐标、飞行时间和最大弹道高进行符合计算,方法与榴弹相同。

采用上述气动辨识结果和符合计算方法,仅以某型155 mm榴弹为例,以弹道计算的落点、最大弹道高和飞行时间作为实际弹道飞行的真值进行符合计算,得到与传统方法的比较结果。从结果中可以看出,采用传统方法能够做到落点准确,但最大弹道高和飞行时间计算误差较大,而采用新方法得到的弹道与实际弹道一致性更好,更能反映弹箭的真实飞行状态,为进一步提高射表编拟精度提供支撑。计算结果如表3所示,表中,Ymax为最大弹道高。

表3 计算结果比较

下一步,将根据遥测姿态试验数据,进一步研究针对攻角、转速的符合计算方法,以实现弹箭质心运动及角运动的全面精确化,将会对射表精度的提升以及射表试验消耗的大幅降低起决定性作用。

4 结束语

本文在基于弹箭全弹道坐标、速度、姿态及转速等飞行诸元精确测量结果的基础上,通过理论研究和仿真计算,对弹箭气动参数准确辨识方法和弹道全面符合计算方法等核心技术问题进行了详细研究,初步形成了基于弹道精确测量的射表编拟新方法。基于弹道精确的射表编拟是一个复杂的难题,理论性强、数据处理难度大,许多问题还有待结合后续试验数据进一步深入研究和完善。