新型光伏阵列等效串联电阻的计算模型
2020-01-09袁丹夫温浚铎王瀚笠
郭 珂,袁丹夫,温浚铎,王瀚笠
(重庆大学,重庆 400044)
0 引 言
太阳能是人类取之不尽的绿色能源,太阳能电站采用光伏阵列将太阳能转化为电能。近年来,光伏发电迅速发展,越来越多地被用于发电系统[1]。太阳能光伏阵列的输出特性不仅与系统本身的内部参数有关,而且会随着外界环境参数的变化而实时变化[2-3]。五参数拟合方法[4]是一种基于光伏电池的工程应用等效电路模型,根据光伏电池内部的电压电流关系列写方程,联立求解光伏阵列的等效串联电阻的方法。但该方法较为繁琐,且对迭代参数初值的精度要求较高,难以满足实际应用要求。
本文从光伏电池的工程电路模型出发,结合数学模型,研究一种实用性强、获取参数简便的等效串联电阻简化计算模型。在此基础上,考虑到实际光伏电站获取实时运行参数较为不便,提出了一种要求参数少,更加符合实际应用的等效串联电阻工程应用模型。本文利用实验测量出的实际值与两种模型的计算值对比验证了模型的精确性。
1 光伏电池的等效电路
建立光伏电池等效电路模型有助于分析光电转换的动态过程,研究光照强度和温度等环境条件对光伏电池I-U输出特性的影响,进而分析光伏电池的等效参数。光伏电池由半导体二极管组成,半导体的P-N结在太阳光的照射下将光能转换成电能[5]。当光伏阵列的辐照度恒定时,光伏电池的光生电流IP不会随电池工作状态变化而变化,因而光伏阵列可以看作是一个恒流源;但当光伏阵列的辐照度发生变化时,IP将成比例变化。假设等效的二极管电流为ID,光伏电池板前后表面的电极以及材料引起内部串联损耗为Rs,光伏电池等效并联电阻为Rsh,理想光伏电池等效电路如图1所示[6-7]。
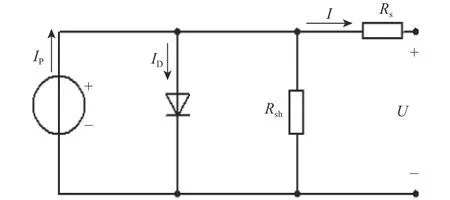
图1 光伏电池等效电路模型
由图1可知:
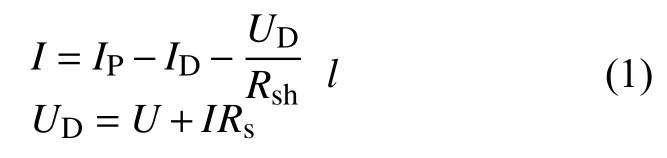
对于通过二极管的电流ID,其大小与二极管的反向饱和电流、二极管端电流和环境温度等有关:
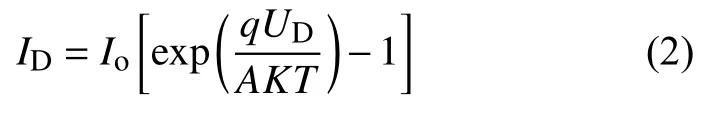
由此推导出太阳能电池的输出电流I:
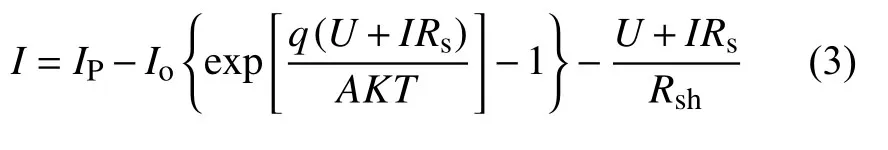
其中q为电荷常数,C;Io为反向饱和电流,A;A为二极管品质因子,1<A<2;ID为流过二极管的电流,A;K为玻尔兹曼常数;T为光伏电池温度,K。
由式(3)可知,光伏电池的I-U输出特性是与光伏电池本身参数和环境参数(如太阳辐照度、电池温度)相关的非线性超越函数。在光伏电池正常工作时,其I-U曲线与P-U如图2所示[8-9],可知光伏电池工作时存在输出最大功率点,其最大功率点电压为Ump,最大功率点电流为Imp。
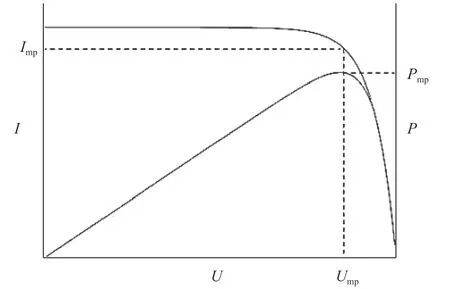
图2 光伏电池正常运行情况下的I-U、P-U曲线图
由图1可知,光伏电池存在等效串联电阻Rs,其大小随故障发生或外界环境条件的改变而改变,是反映光伏电池电压电流特性的一个重要参数。目前计算光伏电池等效参数大多基于五参数迭代拟合的方法,由于输出特性方程为超越方程,求解非常困难,同样由于其中参数随环境条件会发生变化,也不可以直接采用厂家提供的标准等效串联电阻。因此,提出一个实用性强且获取参数简便的等效串联电阻简化计算模型是十分必要的。
2 等效串联电阻简化计算模型
光伏阵列是由许多光伏电池串联和并联形成的,由式(3)得出的光伏阵列理论输出电流数学模型为:
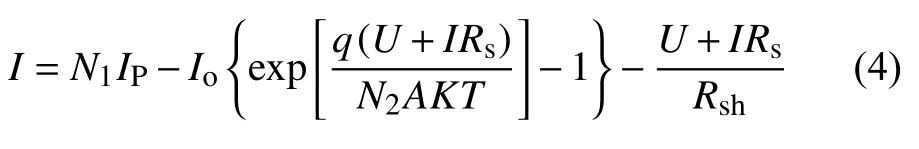
其中N1为光伏阵列并联支路数目,N2为光伏阵列各支路串联支路数目。对于等效并联电阻Rsh,其大小会直接影响光伏电池的开路电压,而光伏阵列的开路电压:
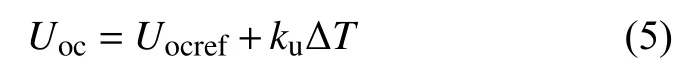
其中ku为光伏阵列的电压温度系数,一般为6.4×10-3,可近似忽略[10],所以开路电压近似为一个常数,即光伏电池发生故障或环境参数发生变化时Rsh基本不会变化,又因为其阻值一般为千欧级别,所以可对式(4)进行相应简化:
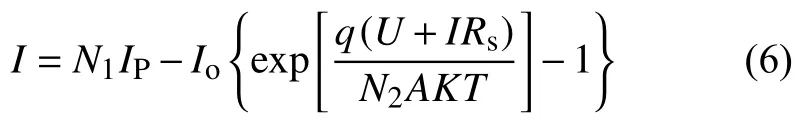
式(6)即为光伏电池输出电流电压的简化数学模型。对于光生电流IP,由于光伏电池的Rs比较小,Rsh相对较大,所以对图1的电路模型:

对于反向饱和电流Io,当光伏电池阵列开路时,此时由式(6)可求出Io:
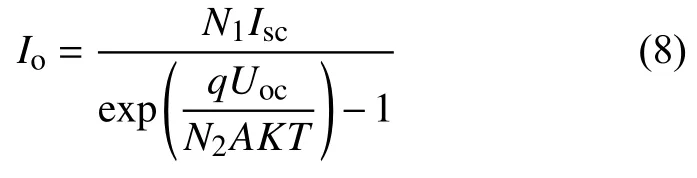
则式(6)可变为:
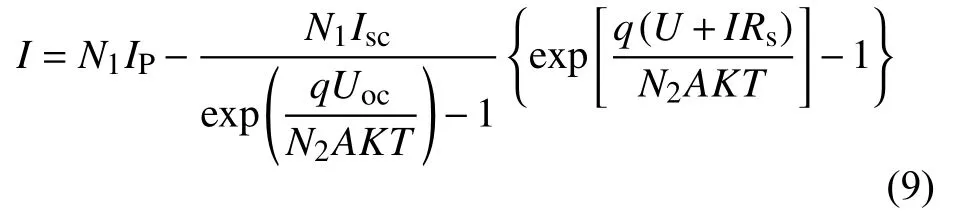
令常量:

当光伏阵列工作于最大功率点时,此时I=Imp,U=Ump,代入式(9),并联立式(7),可以得到光伏阵列最大功率点输出电流与电压关系为:
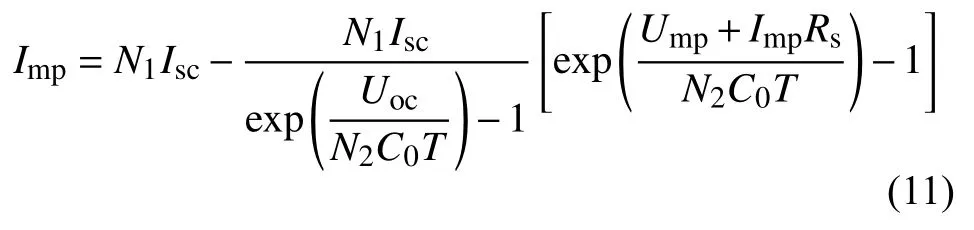
通过式(11),即可求得光伏阵列运行在最大功率点时的等效串联电阻:
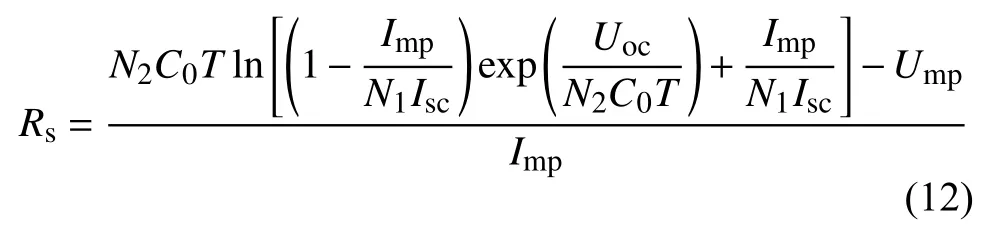
由式(12)可以看出,光伏阵列最大功率点处的等效串联电阻随环境参数的变化而变化。而对于同一光伏阵列,在同一条件下运行时,由于等效串联电阻为低阻值[11],且光伏电站运营均采用MPPT技术,使光伏阵列总是运行在最大功率点附近,所以光伏阵列运行时的等效串联电阻可以由最大功率点的电阻代替。
利用式(12)计算光伏阵列等效串联电阻与以往方法相比更为简单,其参数容易获取,且不需要进行方程的迭代求解。同时,该计算模型可以计算任意环境条件下光伏电池的等效串联电阻,适用于任何已知其环境参数与运行参数的光伏电池的等效串联电阻计算中。
3 等效串联电阻工程应用模型
考虑实际光伏电站运营中,大多数均可得到实时的环境参数,而对于实时测量光伏阵列运行参数(如开路电压Uoc、短路电流Isc、最大功率点电压Ump、最大功率点电流Imp)困难的光伏电站,式(12)仍然存在一些局限性,考虑到[12]:
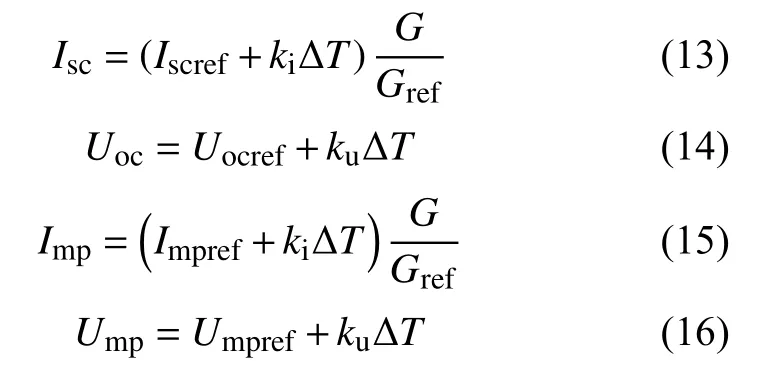
其中,Iscref为光伏阵列标准情况下的短路电流,A;Uocref为光伏阵列标准情况下的开路电压,V;Impref为光伏阵列标准情况最大功率点电流,A;Umpref为光伏阵列标准情况最大功率点电压,V;Gref为标准情况辐照度,1000 W/m2;G为实际情况下的辐照度;电压温度系数ku为 10-3数量级,电流温度系数ki为10-5数量级,可忽略。此时分别将式(13)~(16)代入式(12),得到:
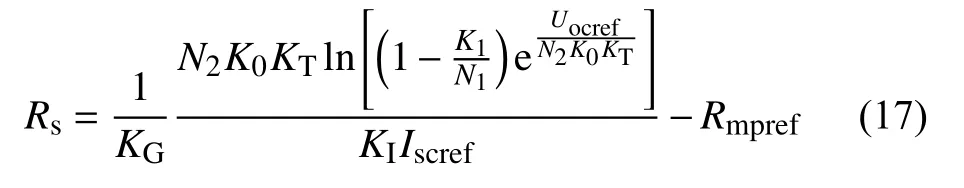
式(17)即为光伏阵列等效串联电阻的工程应用模型。定义常数K0为:

光伏电池理想因子为[13]:
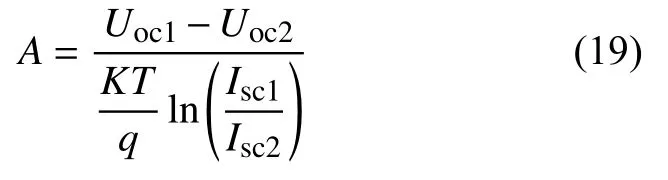
A值不随环境条件改变而改变。
定义光伏阵列辐照度比为:

定义光伏电池温度比为:

其中Tref为标准情况光伏阵列温度,通常取298K。
定义光伏阵列标准电流比为:

定义标准情况下,光伏阵列输出最大功率时,其两端等效的能耗电阻Rmp为:

由式(17)可知,只需知道光伏阵列在标准情况下的开路电压、短路电流、最大功率点电压、最大功率点电流,以及实时的辐照度与光伏阵列温度,便可计算出实时的光伏阵列等效串联电阻。而光伏阵列在标准情况下的运行参数一般由生产厂家给出,所以式(17)的光伏电池等效串联电阻计算模型获取参数更加简单,实用性更强,可适合于各种光伏电站的等效串联电阻计算。但同时该模型也存在一定的局限性,由于其运行参数随环境变化而近似为线性变化,使得其只适用于光伏电池无故障情况下运行,适用范围比式(12)较窄,同时误差也会随参数的简化而增大。
4 等效串联电阻计算模型实验验证
4.1 实验系统搭建
采用18 V/30 W光合硅能电池搭建光伏阵列实验平台,将两组件并联构成简单的SP结构光伏阵列。标准情况(辐照度Gref=1000W/m2,Tref=25℃)下,18 V/30 W光合硅能电池组件的特性参数:Umpref=17.6V,Impref=1.70A,Uocref=21.6V,Iscref=1.95A,最大功率为30W,ku=-0.0029V/K,ki=0.0005A/K。
实验利用EKO(英弘公司)的MP-170 I-V曲线测试仪进行光伏阵列数据采集,可测量任意情况下光伏阵列的运行参数与实时环境参数。
4.2 等效串联电阻实验测量理论值
对于光伏阵列,其等效串联电阻为有限值时,其输出特性在较高正向偏压时偏离指数关系,原因是当正向电压较高时,P-N结进入饱和区,呈现出由等效串联电阻Rs决定的线性关系[14]。由光伏阵列的输出特性曲线可知,在接近开路电压附近,该曲线近似为一条直线,该直线的斜率可以较为精确地表征出光伏阵列的等效串联电阻Rs[15]。
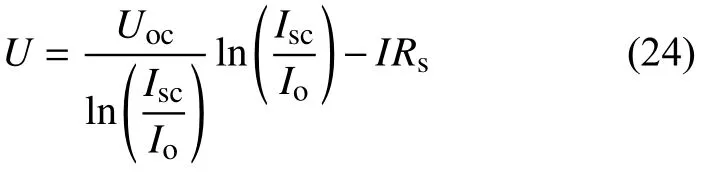
当I→0时,(Isc-I)→Isc,则

式(25)表明,I→0时,I-U曲线有较好的线性关系。将式(25)微分得到:
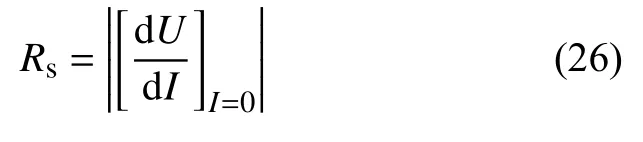
式(26)即为实验求得的等效串联电阻的表达式。因此,测量在I→0附近的I-U曲线的斜率,就能得到光伏阵列的等效串联电阻。
4.3 等效串联电阻计算模型实验验证
为验证模型在不同环境条件下的通用性,确保两种模型的精度均能满足工程要求,利用具体实验对模型进行分析,计算模型的计算值与实际测量值之间的误差。
4.3.1 计算模型实验验证一
实验在太阳能辐照度G=850W/m2,光伏阵列温度T=50℃的条件下进行。在光伏阵列I-U曲线接近于开路电压(式(4))附近选择一定的电流范围,并在此范围内I-U曲线呈现线性关系。根据测量的电压电流值,可近似求出其斜率,从而得出等效串联电阻。实验中得到的数据如表1所示。根据表1的数据,绘制出其关系曲线如图3所示。从图中也可以看出,此时光伏阵列的输出特性曲线在此段是非常接近于线性的,同时也说明该电压电流范围选择合理。根据式(26)可以求出该环境条件下等效串联电阻的实测值为Rs=1.940632Ω。
由I-U曲线测试仪测出光伏阵列在该环境条件下的运行参数为Isc=2.2898A,Uoc=20.6378V,Imp=2.0019A,Ump=16.0585V。
根据式(12),计算出对应条件下光伏阵列等效串联电阻的简化计算模型计算值为2.011934Ω,两者误差为:
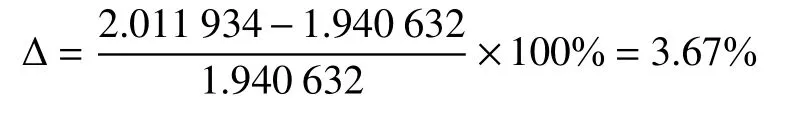
可见简化计算值与实测值的误差在4%以下,满足工程应用精度。
根据式(17),由光伏阵列此时运行条件下的环境参数,计算出光伏阵列等效电阻的工程应用模型计算值为2.082229Ω,两者误差为:
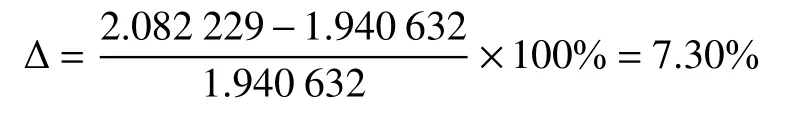
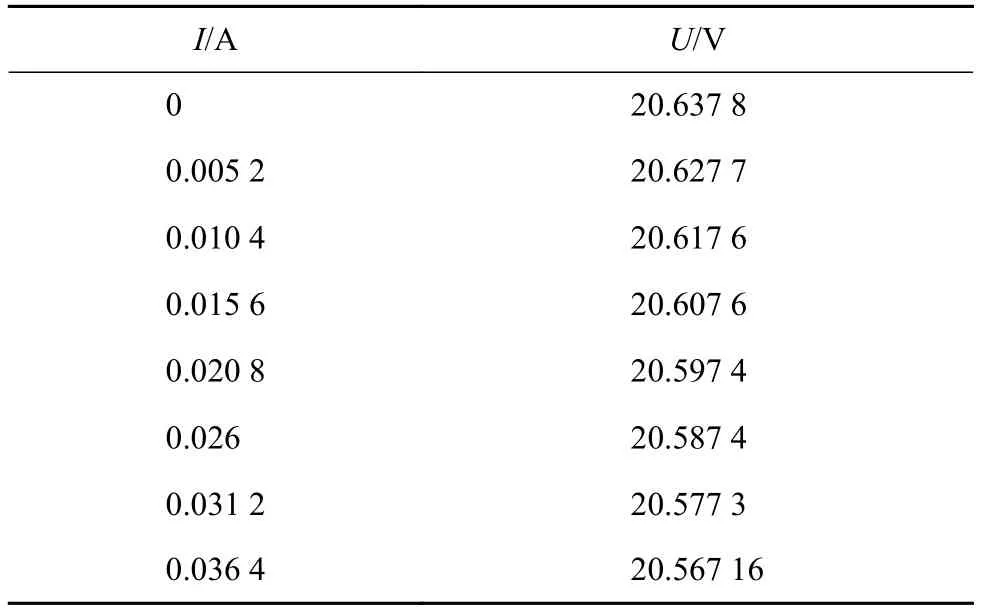
表1 光伏阵列特性曲线实测值(实验一)
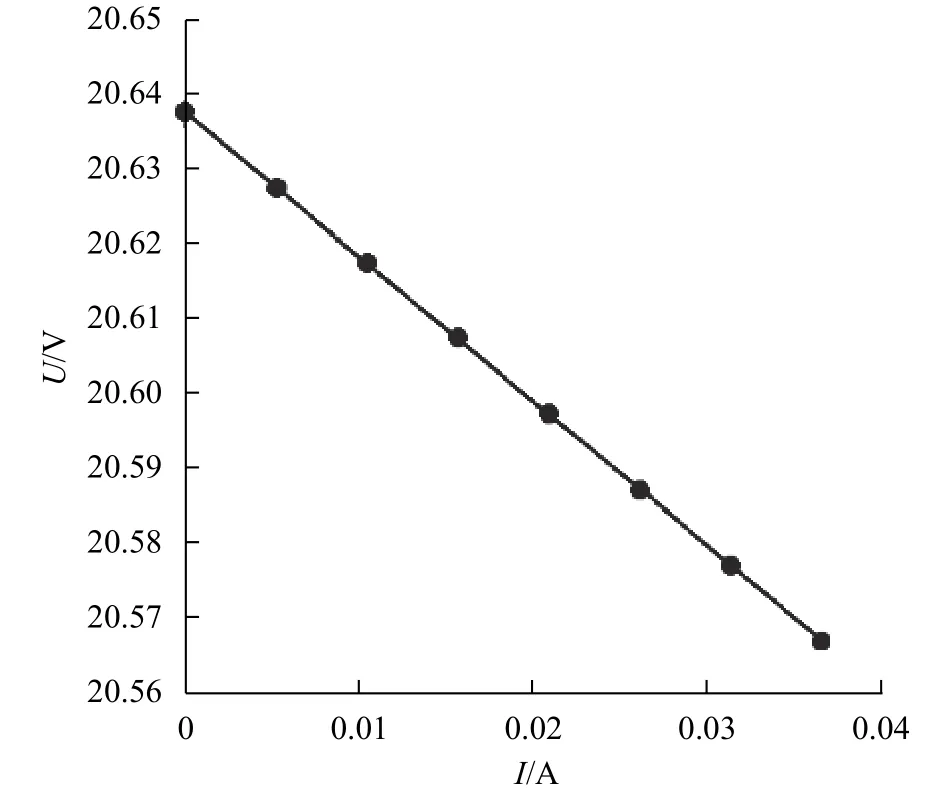
图3 光伏阵列开路电压附近的输出特性曲线(实验一)
可见,工程应用模型误差较简化计算模型偏大,但仍然与实测值较接近,误差仍控制在8%以下,同样满足工程应用精度。
4.3.2 计算模型实验验证二
实验在太阳能辐照度G=1000W/m2,光伏阵列温度T=55℃的条件下进行。在光伏阵列I-U曲线接近于开路电压(式(4))附近选择一定的电流范围,并在此范围内I-U曲线呈现线性关系。根据测量的电压电流值,可近似求出其斜率,从而得出等效串联电阻。实验中得到的数据如表2所示。根据表的数据,绘制出其关系曲线如图4所示。从图中也可以看出,此时光伏阵列的输出特性曲线在此区间是非常接近线性的,同时也说明该电压电流范围选择合理。根据式(26)可以求出该环境条件下等效串联电阻的实测值为Rs=0.920330Ω。
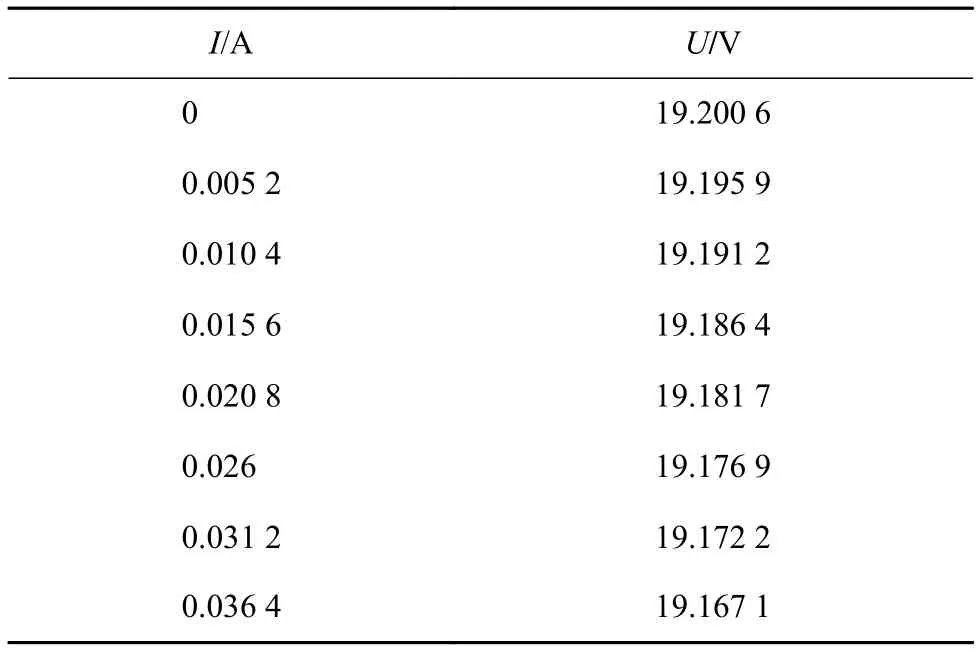
表2 光伏阵列特性曲线实测值(实验二)
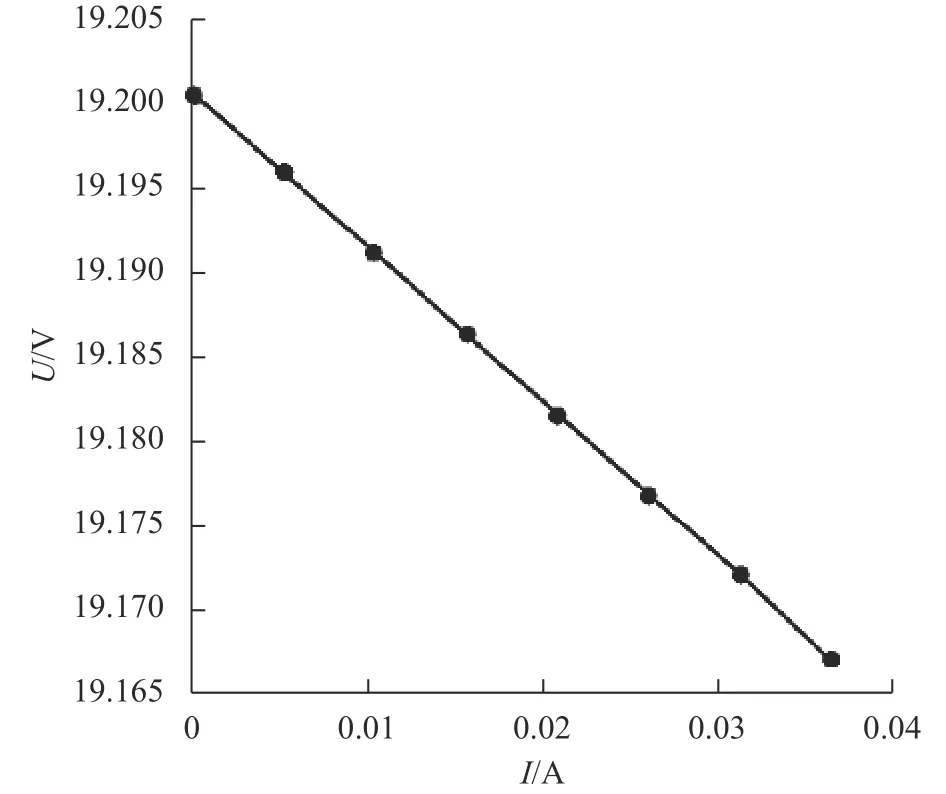
图4 光伏阵列开路电压附近的输出特性曲线(实验二)
由I-U曲线测试仪测出光伏阵列在该环境条件下的运行参数为Isc=3.8768A,Uoc=19.2006V,Imp=3.5582A,Ump=15.2962V。
根据式(12),计算出对应条件下光伏阵列等效串联电阻的简化计算模型计算值为0.921501Ω,两者误差为:
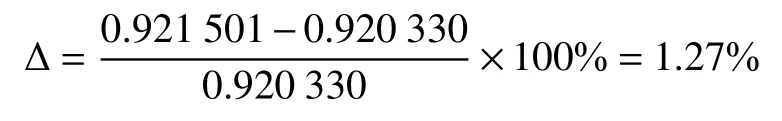
可见简化计算值与实测值的误差在4%以下,满足工程应用精度。
根据式(17),由光伏阵列此时运行条件下的环境参数,计算出光伏阵列等效电阻的工程应用模型计算值为0.987713Ω,两者误差为:
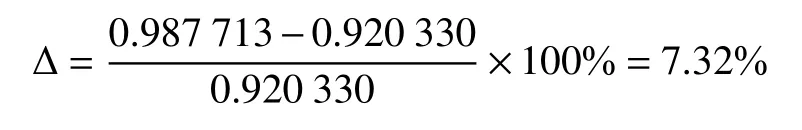
可见,工程应用模型误差较简化计算模型偏大,但仍然与实测值较接近,误差仍控制在8%以下,同样满足工程应用精度。
5 结束语
本文基于光伏阵列的等效电路模型,提出了两种新型的光伏阵列等效串联电阻计算方法。在简化模型方法中,只需要光伏阵列运行过程中的4个运行参数(短路电流Isc,开路电压Uoc,最大功率点电流Imp,最大功率点电压Ump),即可准确求出此时光伏阵列的等效串联电阻;在工程应用模型中,只需要光伏电池生产厂家提供的标准情况下的4个技术参数(短路电流Iscref,开路电压Uocref,最大功率点电流Impref,最大功率点电压Umpref),并通过此时光伏阵列的环境参数,即可快速地求出光伏阵列等效串联电阻。通过两种计算模型结果与实际测量结果的比较,得知两种模型的误差均在8%以下,可以较好地满足工程应用精度条件。
