基于变分模态分解的超声检测信号降噪研究

王大为，王召巴，李 鹏，陈友兴，李海洋

(1.中北大学信息与通信工程学院，山西 太原 030051; 2.山西师范大学物理与信息工程学院，山西 临汾 041000;3.西安近代化学研究所，陕西 西安 710065)

0 引 言

变分模态分解[1]（variational mode decomposition，VMD）是Dragomiretskiy于2014年提出的一种信号处理理论，该方法认为任意信号都可分解为一系列带宽有限的模态函数的线性组合，将信号处理问题转化为变分模型求解问题，通过迭代搜索变分模型的极值确定每个模态的中心频率和带宽，从而实现对原信号的分解。变分模态分解因其有严密的数学理论推导，克服了经验模态分解[2]（empirical mode decomposition，EMD）缺乏理论支撑、出现模态混叠和端点效应等不足，一经提出就引起了国内外学者广泛关注，已在生物组织健康诊断[3-4]、信号增强和辨识[5-6]、轴承故障诊断[7-8]等领域进行了试验性研究和成功的应用。超声检测是目前国内外使用频率最高且发展较快的一种无损检测技术，在工业生产等实践中得到了广泛应用[9-10]。信号降噪与特征提取是超声检测数据处理的关键技术，同时也是超声无损检测的核心环节，其性能优劣直接影响着无损检测结果的表征，因此对其进行研究有重要的学术意义和实用价值[11]。

本文将变分模态分解方法引入到超声检测信号处理中，针对变分模态分解可以将待处理信号分解为一系列有限带宽的模态函数这一特征，利用变分模态分解原理对超声检测信号和噪声分解得到的各模态频域特性的差异，即超声信号被分解为信号频带内一系列窄带信号，而高斯噪声被分解到[-π,π]整个频带内的一系列宽带信号，以此为依据提出了基于变分模态分解的超声信号降噪方法。该方法通过变分模态分解，计算各模态带宽和中心频率，选择信号模态，由信号模态重构无噪信号4步实现对超声信号的降噪。此外，为提高超声仿真信号和实测超声信号的匹配度，本文提出了一种改进的高斯超声信号模型。

1 变分模态分解原理

变分模态分解以每个本征模态函数是其中心频率附近的窄带信号为准则构造变分模型，通过交替方向乘子算法（alternate direction method of multipliers,ADMM）[12]在其频域进行迭代求解，进而将输入信号分解为一组本征模态函数的线性组合。

1.1 变分模型构造

在变分模型中本征模态函数（intrinsic mode functions，IMF）定义为调幅-调频信号，其表达式为：

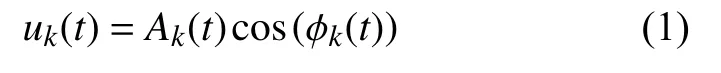
其中瞬时幅值Ak(t)为非负函数，相位ϕk(t)为单调非减函数。

瞬时频率为：

瞬时频率和瞬时幅值相对于相位应是缓慢变化的，即在足够长的时间间隔[t-δ,t+δ]（δ≈2π/ωk(t)）上，本征模态函数可以看作幅值为Ak(t)，频率为ωk(t)的余弦波。

变分模态分解的目标是将输入的实信号f分解为一组本征模态函数uk(t)的线性组合。分解过程中要求本征模态函数能表征原信号的同时应具备足够的稀疏性。通过以下3步来构造变分模型：

1）为得到信号的单边频谱，对每个模式uk(t)进行希尔伯特变换并求其对应的解析信号：

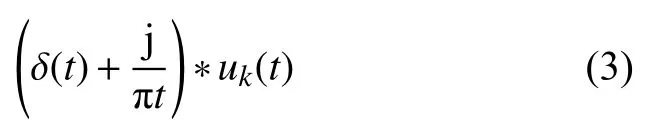
2）估计每个模式的中心频率ωk(t)，然后通过混频将其解调到基带：

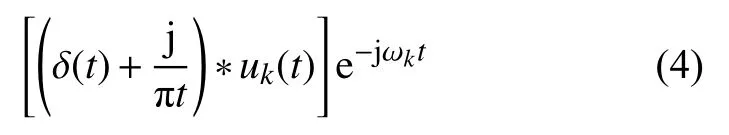
3）利用H1高斯平滑度估计解调信号的带宽[1]。

因此，基于以上3点可得IMF的变分约束模型为：

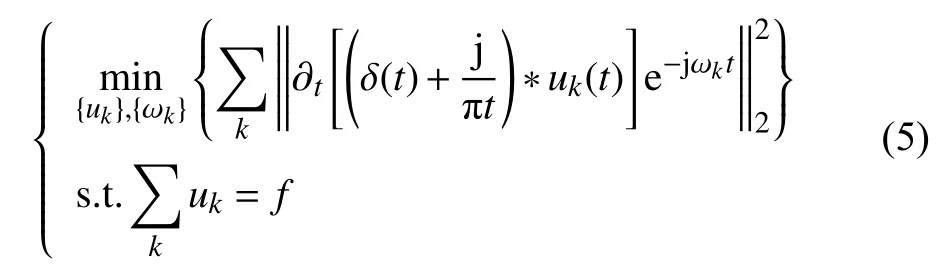
1.2 变分模型求解

为求解上述约束变分模型，通过引入二次惩罚项和拉格朗日乘子使构造的约束变分模型变为无约束变分模型。

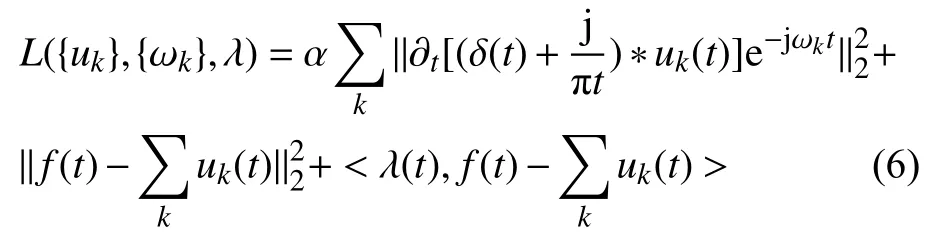
通过交替方向乘子算法在频域求解该方程[1]，其主要步骤如下：

输出：分解得到的K个模式。

2） 令n=n+1，并根据下式分别更新每个模式及其中心频率，其中k=1，2，∙∙∙，K。

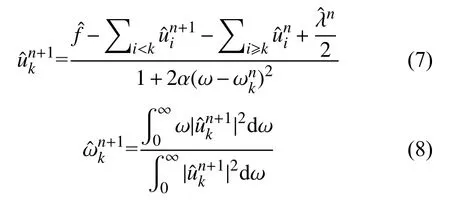
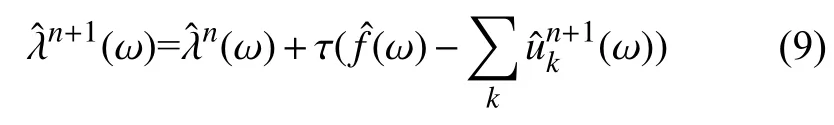
4）根据下式判断是否满足收敛条件，如果收敛则输出分解得到的K个模式，否则返回步骤2）继续迭代分解：

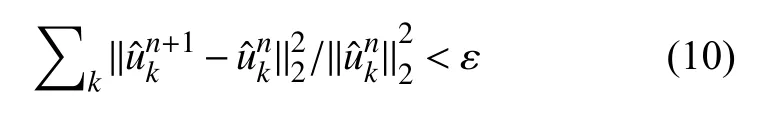
以上就是变分模态分解的基本过程。需要特别说明的是上述过程是在频域进行求解，其中=FT(x(t))表示对x(t)做傅里叶变换。

2 VMD在超声信号降噪中的应用

2.1 超声信号模型

在超声脉冲回波检测中超声回波信号通常是一个被超声探头中心频率调制的宽带信号[13]，其表达式为

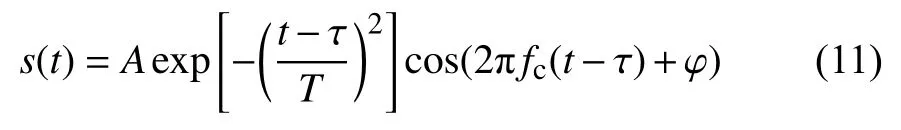
其中A为反射回波幅度；T为带宽因子；τ为回波到达时间；fc为发射超声脉冲的中心频率；φ为初相位。

该模型一经提出就得到广泛应用，其在超声信号数值分析和仿真方面有着重要作用[14-15]。但是该模型存在两点不足之处：1）根据参数的物理意义，在t＞τ的范围内该模型才有波形，而在t＜τ范围内该模型无波形或波形无意义；2）该模型仅能模拟时域半边带的高斯包络，这与实测中的超声信号有很大差别。为提高在信号起始时刻仿真超声信号和实测超声信号的相似度，本文提出一种改进的超声信号模型，其表达式为：

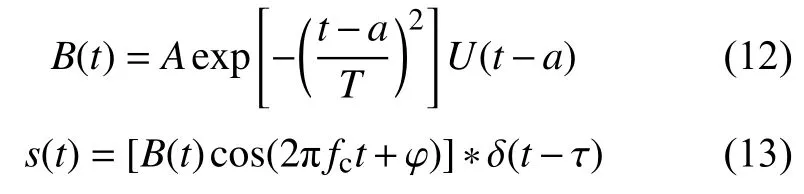
其中，a为包络函数B(t)的起点，U(t)为单位阶跃函数，δ(t)为Dirac函数，*表示卷积运算，其他参数物理意义同式（11）。

2.2 VMD降噪原理

由于超声信号具有特定的结构，而高斯噪声没有固定的结构；表现在频域超声信号是一有限带宽信号，而高斯噪声对应的频谱分布在数字频率ω∈[-π,π]整个频带内。如图1和图2所示分别为采用VMD对超声信号和高斯噪声进行6层分解得到的频谱图。

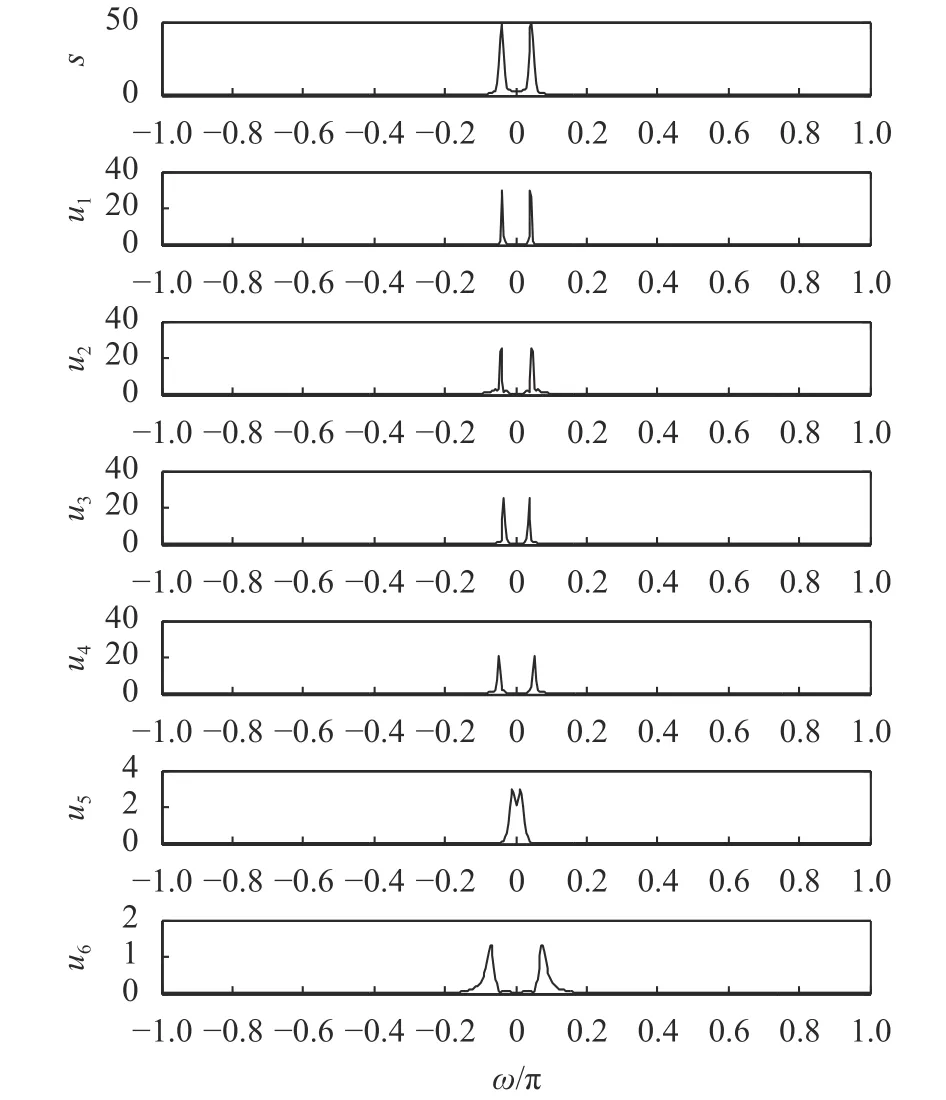
图1 无噪信号VMD分解谱

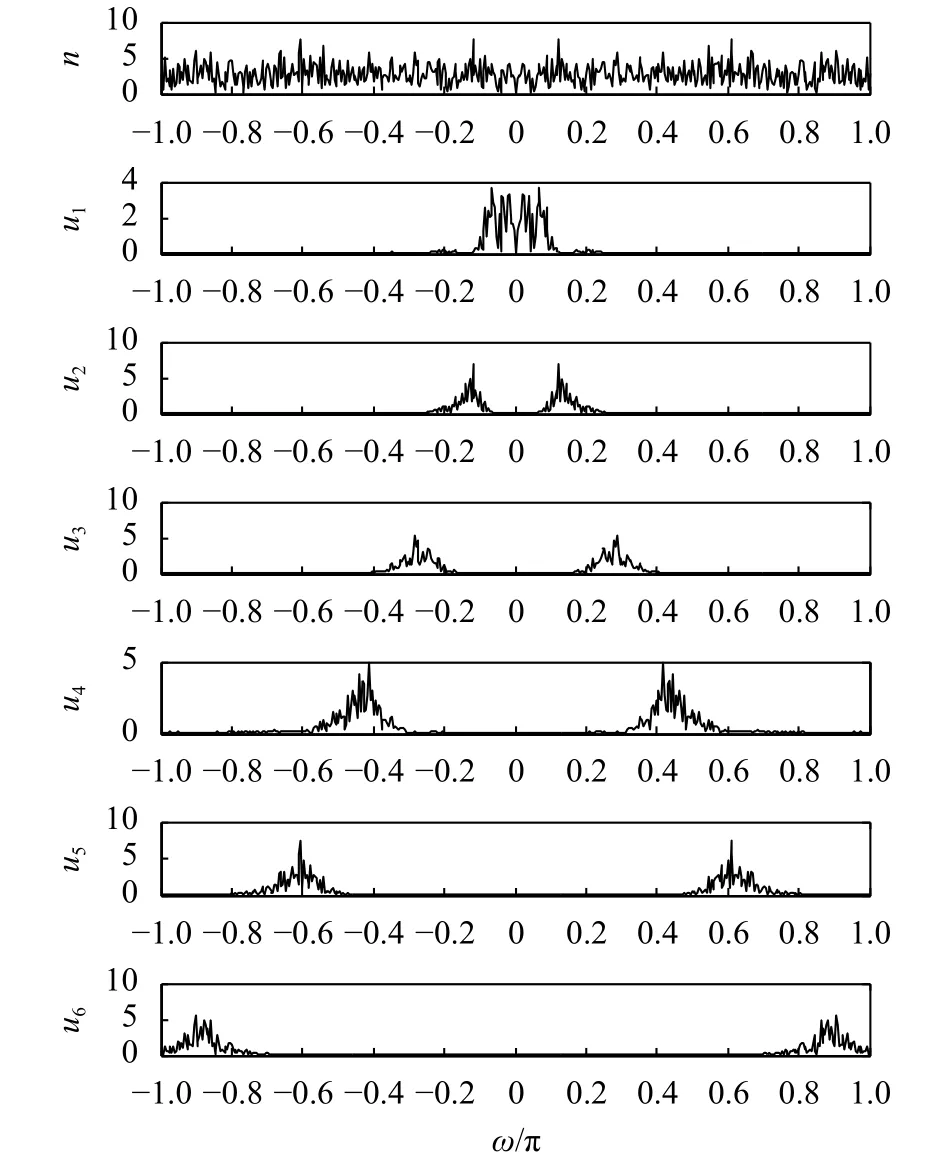
图2 噪声VMD分解谱图

图1中s为无噪超声信号的频谱图，u1~u6分别为VMD分解后的6个模态的频谱图，从图中可以看出VMD将原信号s的频谱在频域内分解为6个中心频率不同的窄带信号，每个模态对应于原始信号s频谱的一部分。

图2中n为噪声的频谱图，u1~u6为对噪声进行VMD分解后得到的各模态的频谱图。从图中可以看出VMD将噪声分解为频带内不同中心频率的宽带信号。对比图1和图2可得出结论：对于K层VMD，信号和噪声都被等间隔地分解为各自频带内K个模式。由于超声信号带宽相比于高斯噪声带宽较窄，对于相同的分解层数K，VMD分解后噪声模态对应的带宽远大于信号模态的带宽。根据这一原则可在频域分辨超声信号模式和噪声模式，基于VMD的超声信号降噪方法具体步骤如下：

1）初始化，设定待分解层数K。

2）对给定的含噪超声信号s(t)，求其傅里叶变换，并令=FT(s(t))，根据1.2中变分模态分解过程对其进行VMD分解。

3） 计算每个模式的带宽和中心频率，依据信号对应窄带模式，噪声对应宽带模式原则，对分解后的模式进行分类，选择具有窄带特性的模式。

4） 根据选择的窄带模式重构超声信号。

3 实验与仿真分析

当前广泛用于信号降噪结果评价的指标有均方误差MSE、波形相似系数NCC和重构信噪比ESNR[16]。均方误差越小，重构信噪比越大，波形相似系数越接近于1表明降噪效果越好。

3.1 超声信号模型

当本文提出的超声信号模型参数[A,T,fc,φ]=[0.8, 100, 0.1, 0]时，参数a取不同值时对应的超声仿真信号如图3所示。

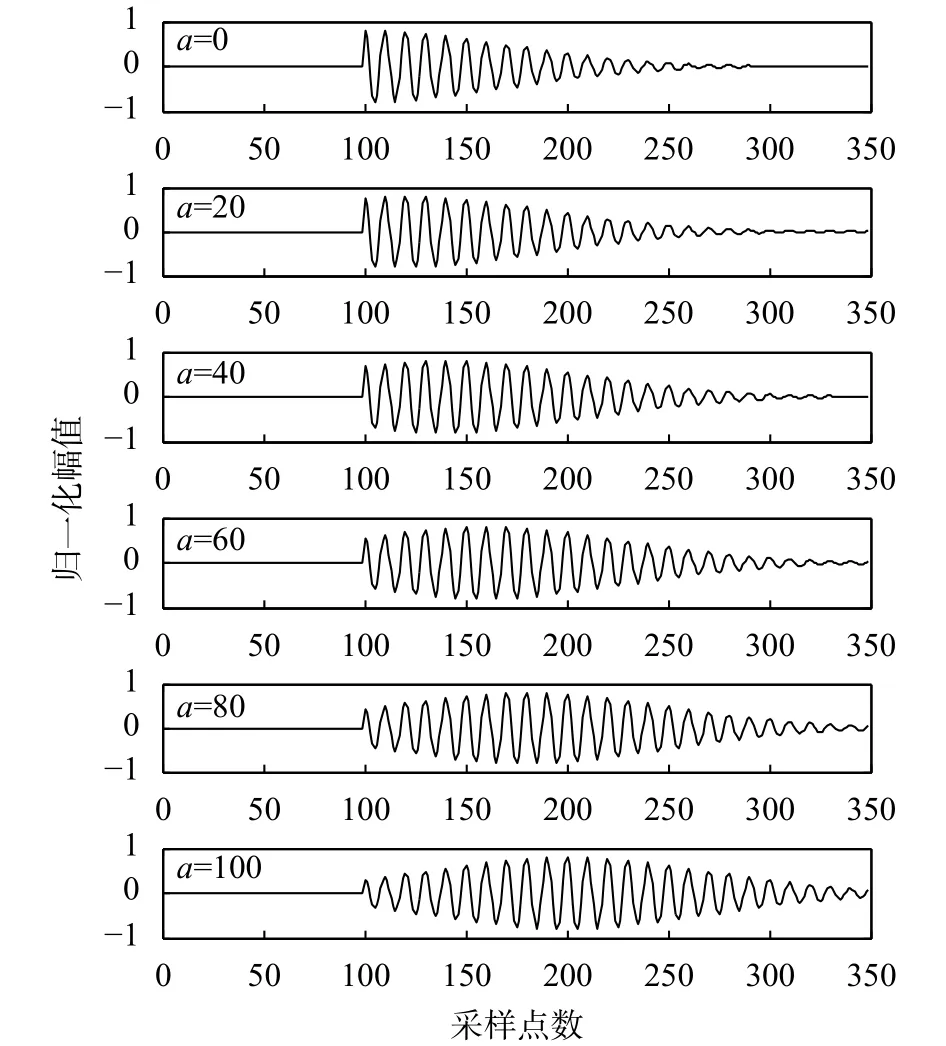
图3 超声仿真信号

当a=0时，本文提出的超声信号模型退化为高斯超声信号模型。对比图3中各波形可以看出，改进的超声信号模型相比高斯模型包含的超声信号包络信息更丰富，随参数a变化可以模拟起始时刻不同包络的超声信号；而高斯模型起始时刻包络是固定不变的。因此，改进的超声信号模型是高斯模型的拓展，比高斯模型包含的包络信息更丰富。

3.2 不同模型比较

为验证本文提出的超声信号模型性能，将本文模型、指数模型[15]分别和在实验室中用RITEC RAM-5000-SNAP超声检测系统采集的超声回波信号[16]进行匹配，其结果如图4所示。经计算，指数模型和实测超声信号的均方误差为0.022 3，波形相似度为0.916 0；本文改进的高斯模型和实测超声信号的均方误差为0.008 3，波形相似度为0.973 3。因此，无论直观对比效果还是客观评价指标，本文提出的超声信号模型都优于指数信号模型。

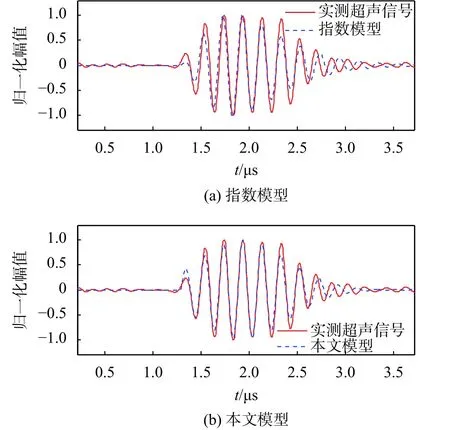
图4 不同模型效果对比

3.3 降噪性能分析

当K=5时，对含噪超声信号（SNR=10 dB）进行VMD分解后得到的各模态频谱图，如图5所示。

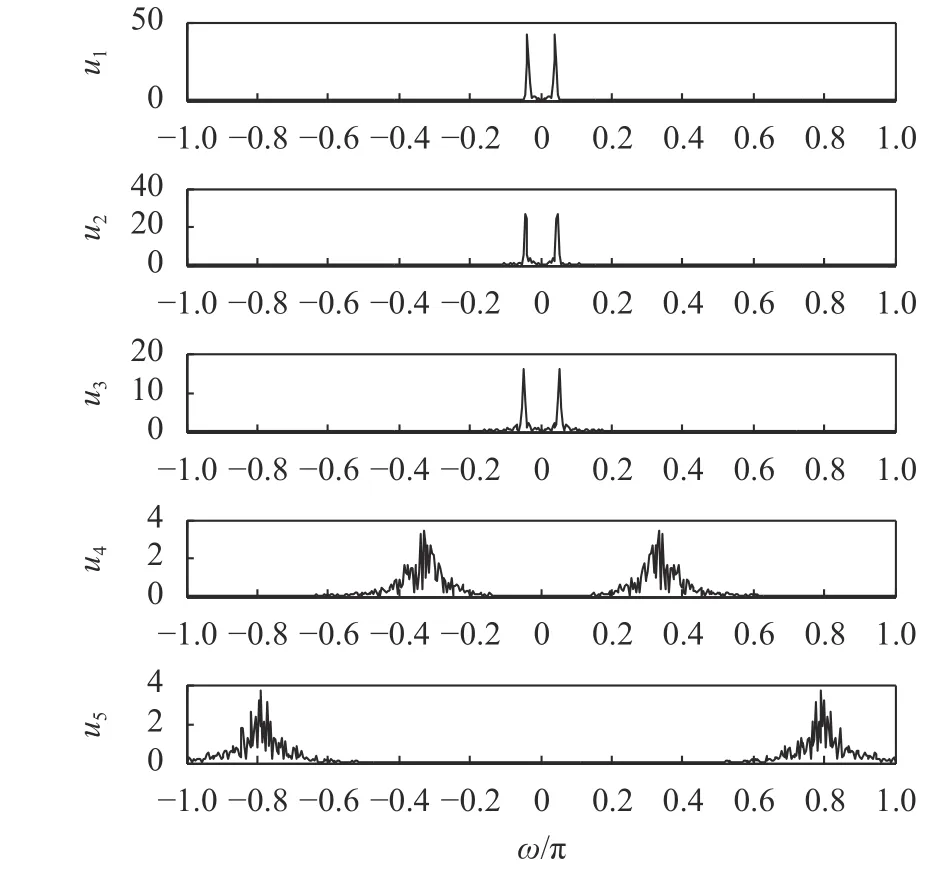
图5 含噪信号分解频谱

从图中可以看出，u1~u3模式的频谱带宽窄且幅值大，由前述分析知这是信号模式的典型特征；而u4、u5中频谱带宽较宽且幅值相对小，为噪声模式的特征；由u1~u3模式对应的信号在时域相加后得到的重构超声信号如图6所示。

经计算，相比原始无噪超声信号，降噪后信号的均方误差MSE=0.000 7，波形相似系数NCC=0.994 0，重构信噪比ESNR=19.237 4 dB。

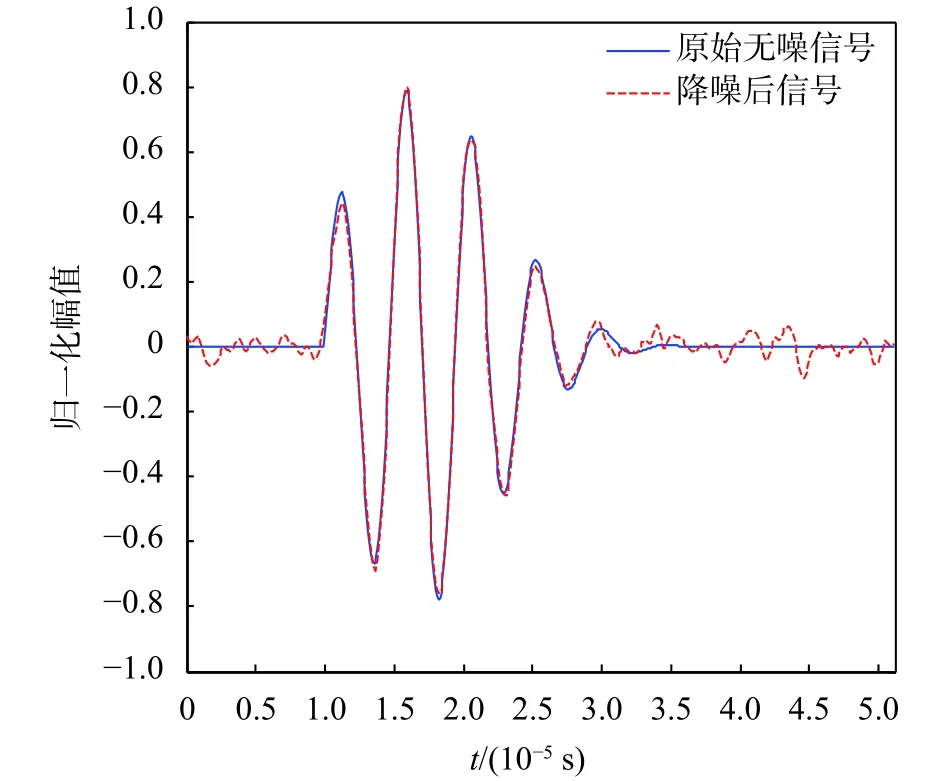
图6 降噪效果对比

3.4 不同方法性能比较

为验证本文方法的降噪性能，分别采用本文提出的VMD降噪方法、小波降噪方法及EMD降噪方法对图7（a）中无噪超声信号加入噪声后进行降噪处理，当信噪比为0 dB时降噪结果如图7所示。

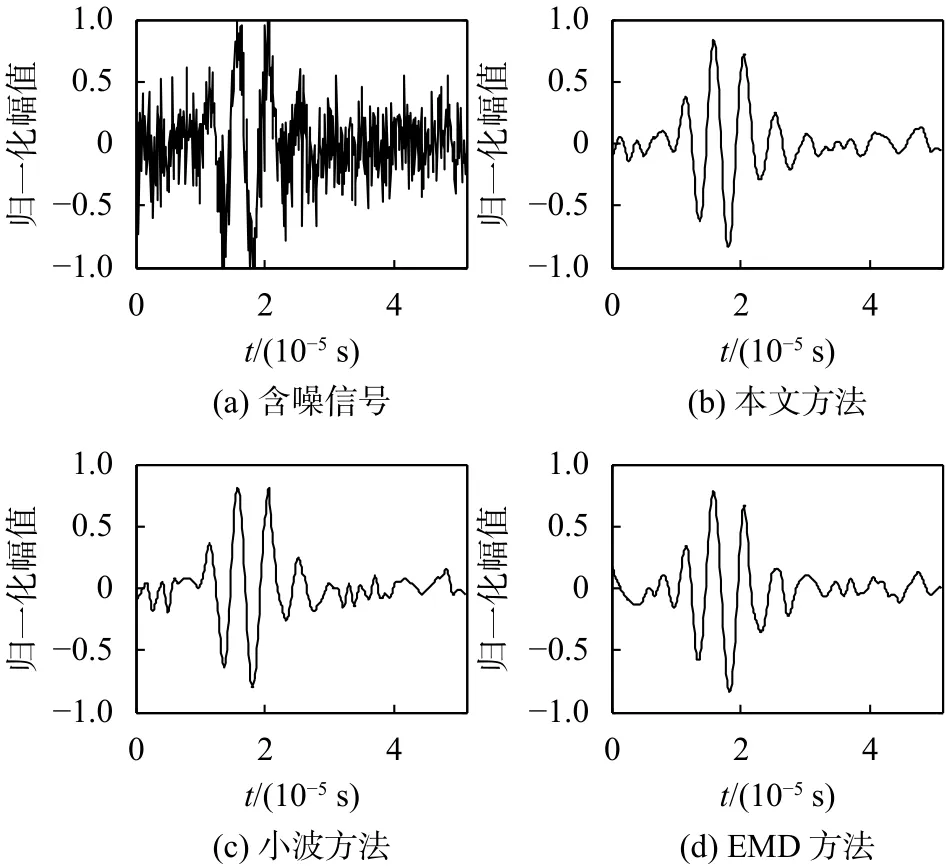
图7 不同方法比较

不同方法对应的评价指标如表1所示。

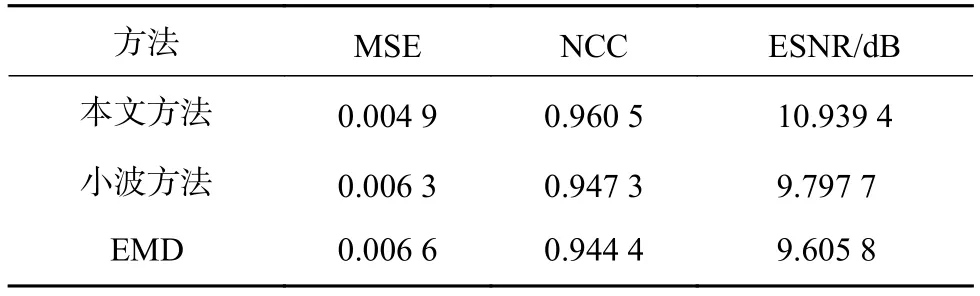
表1 降噪效果评价指标

由图7和表1知，在对如图7(a)中所示的超声检测信号进行降噪处理时，本文提出的方法效果要好于小波方法和EMD方法。

4 结束语

本文将变分模态分解理论应用到超声信号处理中，提出了一种基于变分模态分解的超声信号降噪方法。通过变分模态分解，计算各模态带宽和中心频率，选择信号模态，根据信号模态重构无噪信号4步实现对超声检测信号的降噪。此外，为提高超声仿真信号和实测超声信号的匹配度还提出了一种改进的超声信号仿真模型，相比指数模型和高斯模型，本文提出的仿真模型与实测超声信号更匹配。