基于近似计算技术的FPRM逻辑功耗优化

王一琛, 王伦耀, 夏银水, 储著飞

基于近似计算技术的FPRM逻辑功耗优化

王一琛, 王伦耀*, 夏银水, 储著飞

（宁波大学 信息科学与工程学院, 浙江 宁波 315211）

提出了一种基于近似计算技术的Fixed Polarity Reed-Muller(FPRM)逻辑功耗优化算法, 该算法包括基于信号概率和跳变密度的固定极性Reed-Muller(RM)函数动态功耗模型, 基于遗传算法的以功耗优化为导向的RM逻辑极性搜索方法, 以及利用双锐积运算的RM逻辑错误率计算方法. 在错误率的约束下, 通过有选择性地删减部分乘积项, 实现功耗优化. 提出的算法用C语言实现, 并用MCNC Benchmark电路测试. 结果表明: 与原始FPRM电路功耗相比, 在平均错误率为3.21％时, 电路动态功耗平均减少了22.77％.

近似计算; 错误率; 极性搜索; 功耗优化

逻辑功能正确一直是传统数字逻辑在设计时的首要条件, 且为保证功能正确不惜牺牲电路的面积、功耗、时延等性能指标. 但在有些应用中,如图像、音频处理, 待处理的数据具有一定的容错性, 在某一范围内的计算错误不会影响电路的实际应用, 待处理数据的这种容错特性意味着可以适当降低计算精度, 进而实现电路其他性能指标的提升, 这种非精确计算称之为近似计算. 利用近似计算技术实现电路的逻辑优化称为近似优化. 目前,近似计算已成为数字集成电路设计中一个新的重要策略.

逻辑函数通常采用2种基本形式, 既可采用基于“与/或/非”运算的传统布尔(Traditional Boolean, TB)逻辑, 也可采用基于“与/异或”运算的Reed- Muller(RM)逻辑. 目前, 在TB逻辑上开展的研究主要包括基于近似计算的二级逻辑电路优化[1-3]、多级逻辑电路优化[4-5]等. 多数优化算法以乘积项为基础实现近似函数的构造和近似度计算, 但是也有基于伪乘积项[6]或借助二元决策图(Binary Decision Diagram, BDD)来实现[7].

除TB逻辑外, RM逻辑正吸引越来越多研究者的兴趣, 其原因包括: (1)随着集成电路技术的发展, 构成RM逻辑的“异或”门无论是速度、功耗还是面积都获得极大的改进, 使之更加适合实际应用. (2)与TB逻辑相比, RM逻辑在算术及通信电路、可逆逻辑设计[8]、可测试方面等应用具有优势. (3)近一半的电路, 如采用RM逻辑进行综合可获得更加简单的结果. (4)有些新的器件具有“异或”特性, 相比互补金属氧化物半导体(Complementary Metal Oxide Semiconductor, CMOS)电路, 新器件在“异或”运算实现将变得极为简单.

目前, 已有不少RM逻辑功耗优化方法, 包括RM函数极性搜索方法、多输入XOR门阵列分解方法; 搜索方法包括遗传算法[9]、粒子群算法[10]、Min-Huffman算法[11]等. 上述优化算法均没有涉及错误引入对功耗优化的影响.

本文主要研究近似计算技术在RM逻辑电路功耗优化中的应用, 提出了一种利用近似计算技术实现FPRM逻辑电路功耗优化的方法, 即建立以信号概率和跳变密度为参数的RM逻辑电路动态功耗数学模型;并在错误率约束下, 利用提出的优化策略删减部分乘积项, 实现FPRM逻辑电路动态功耗的优化.

1 RM逻辑电路的动态功耗数学模型

逻辑电路的功耗包括静态功耗和动态功耗, 动态功耗是功耗的主要部分, 由电路中所有节点电容充放电引起, 可用式(1)表示:

式中:dp为动态功耗;为电路总节点数;dd为电源电压;c为第个节点的等效电容;w为第个节点的开关活动率, 其大小等于第个节点单位时间内平均充放电次数.

从式(1)可知, 只要减小任何一个参数都可以实现电路的动态功耗优化. 本研究主要通过降低电路开关活动率w来实现电路的功耗优化.

对于第个节点w, 其大小与加在该节点上的信号的概率()和跳变密度()有关. 其中()等于信号在时间内取值为逻辑1的比例.

信号的跳变密度()等于在单位时间内的跳变次数, 即在时间内的跳变次数n()与比值.

从式(3)跳变密度定义可看出, 信号的跳变密度和开关活动性本质一致, 因此本研究用信号跳变密度来表示开关活动性.

RM逻辑是由“与/异或”运算构成的二级逻辑,因此RM逻辑电路功耗估算可以通过对与门阵列和异或门阵列功耗估算来实现. 考虑到多输入逻辑门均可以分解成二输入逻辑门的组合, 因此本研究通过对二输入与门和异或门功耗的估算来实现RM逻辑电路的功耗估算.

对于输入为1和2, 输出为2的二输入与门,设1和2的信号概率分别为(1)和(2), 跳变密度分别为(1)和(2). 考虑到二输入与门中只有一个输入信号为高电平时, 另一个信号的跳变才能传输到输出端, 因此输出端2的跳变密度(2)可以表示为:

式中:∈[1,2,…,],≠.

对于有个输入变量的异或门, 由于输入端的任何跳变都会引起输出端的变化, 因此输出端的跳变密度(y)就等于各输入信号跳变密度之和, 即:

利用式(5)和式(6)可以计算出由个与门,个异或门构成的RM逻辑电路所有内部节点的总的跳变密度RM, 即:

式中:AND()表示第个与门输出跳变密度;XOR()表示第个异或门输出跳变密度.

在RM逻辑电路的功耗优化中, 极性变换是实现RM逻辑电路功耗优化的一种有效手段. 以式(8)为例:

假设3个输入变量的概率与跳变密度分别为(1,2,3)=(0.7,0.8,0.3),(1,2,3)=(0.2,0.4,0.1),则由式(5)~(7)可以得到: 当极性分别为6和0时, 式(8)的RM函数对应总的信号跳变密度分别为0.244和0.878. 因此, 可以通过极性变换实现RM逻辑电路的功耗优化[12].

2 近似RM逻辑的错误率计算方法

基于近似计算的RM逻辑函数优化可以通过增减原函数的乘积项来实现RM逻辑函数面积优化, 减少电路节点数, 从而实现RM逻辑函数功耗优化.

显然式(9)要比式(8)简单. 从图1可知, 通过引入特定的错误可实现RM逻辑函数的简化. 图1(b)中可能的输入有23=8种, 只有输入(x1x2x3)=(011)时, 输出错误, 因此错误率为1/8.

图2 原函数及其近似逻辑函数的卡诺图表示

从图2的例子中不难发现, RM逻辑与TB逻辑近似优化不同, 主要表现在: (1)引入取值为“0”的某些乘积项, 可简化RM表达式, 但不增加错误输出. (2)在错误率计算方面, 对于TB逻辑而言, 可以直接通过比较近似函数的乘积项集合与原函数的乘积项集合的差异, 得到引起错误输出的乘积项的集合, 进而计算出错误率. 但对RM逻辑, 近似函数的乘积项集合与原函数的乘积项集合的差异不一定就是引起错误输出的乘积项的集合, 因为差异部分可能包含了偶数次逻辑覆盖, 即RM逻辑与TB逻辑的错误率计算方法不同. 上述差异使得原来适用TB逻辑近似优化的方法不能直接用于RM逻辑的近似优化.

算法1 double_disj_sharp (er,out)

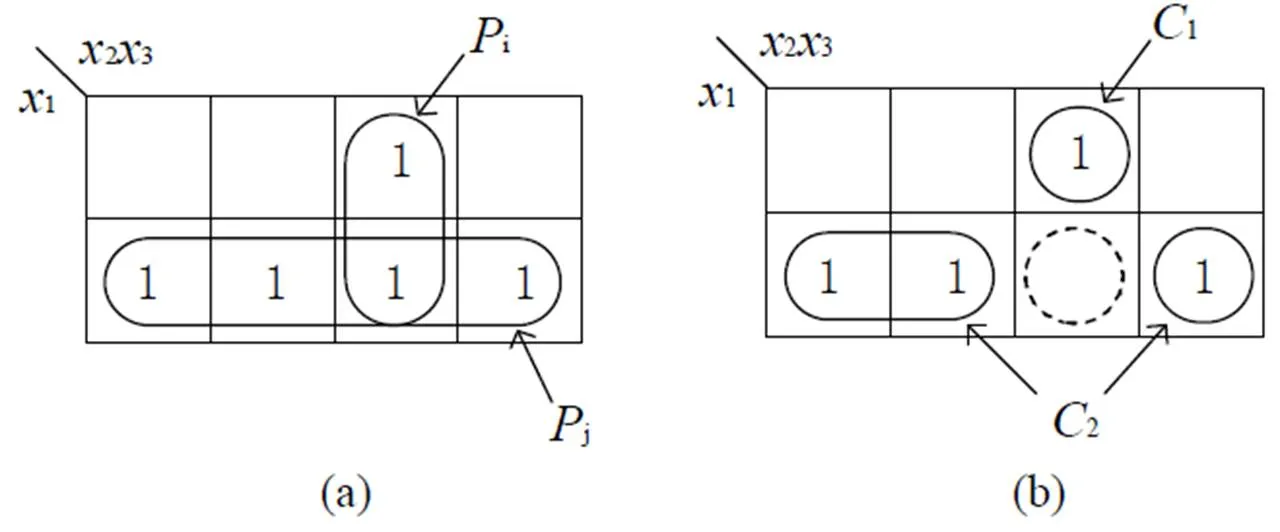
图3 利用双锐积运算去除RM逻辑中的偶数次逻辑覆盖

3 基于近似计算技术的FPRM逻辑电路功耗优化算法

基于近似计算的FPRM逻辑电路功耗优化算法大致可分为2个部分: (1)是利用遗传算法实现以功耗优化为导向的RM逻辑的极性搜索, 得到功耗优化下的FPRM表达式; (2)引入近似计算技术, 在错误率约束下, 通过删除FPRM函数中特定的乘积项实现功耗的进一步优化.

算法2为基于近似计算技术的FPRM逻辑电路功耗优化代码, 其中为了方便实现TB逻辑向FPRM逻辑转化, 先将测试电路表示为不相交乘积项之“或”形式, 然后利用基于不相交乘积项列表技术[17]实现TB逻辑向FPRM逻辑转化.

算法2 FPRM_pwr_opt_ap(dis)

算法2中step1用遗传算法实现以功耗优化为导向的FPRM函数极性搜索, 得到FPRM函数的乘积项构成集合RM_pwr; step2用式(5)计算RM_pwr中各RM乘积项的跳变密度, 并按照跳变密度进行降序排序; step3按照乘积项的跳变密度大小从大到小试探性地逐个删除, 并将删除的乘积项放到er; step4利用双锐积运算去除er中乘积项之间偶数次覆盖, 并将不存在偶数次覆盖的乘积项存储在out; step5中[out]表示乘积项集合out包含的最小项的数量. 由于双锐积后的乘积项均为不相交乘积项, 因此[out]大小等于每个不相交乘积项包含的最小项数量的和. 另外,为函数的输入变量数.

在执行step3到step5过程中, 如果移除某一乘积项p后, 发现>0, 则程序会放弃删除, 转而试探性往下删除其他乘积项, 并判断是否符合错误率约束条件. 循环执行step3到step5, 直到无法满足≤0,0为设定的错误率.

4 实验结果和分析

本文提出的RM逻辑功耗优化算法在win7 64位操作系统4GB内存环境下运行, 用C语言编程实现, 采用MCNC Benchmark电路进行验证. 在多输出逻辑函数处理时, 常用的处理方法是将多输出函数转化为单输出函数, 然后按照单输出函数进行处理. 本文只有输出相等的乘积项才进行比较处理. 文中遗传算法种群最大个体为30, 最大迭代数为50, 染色体交叉率为55％, 变异率为16％. 电路的功耗用电路内部节点总的跳变密度表示. 实验中每个电路输入信号的概率与跳变密度随机产生, 并将近似计算的错误率阈值设置为不大于5％.

表1为实验结果, 其中“//”分别对应测试电路的输入数、输出数和乘积项数;pr表示功耗减少百分比, 运算时间单位为秒:

式中:Power(_)和Power()分别表示在相同输入信号下原电路和经近似计算优化后电路总的信号跳变密度.

表1 实验结果

从表1可知, 在错误率阈值5％的前提下, RM逻辑的功耗优化明显. 如电路sym10和pcle等电路功耗少了56.29％和50.31％, 优化效果明显. 但也有部分电路, 如pm1和cc电路功耗减少不明显, 分别减少了7.48％和6.63％, 其主要原因是在采用FPRM形式下, pm1和cc的乘积项之间相互交叠比较复杂, 删除少量的乘积项就会带来较大的错误率, 导致在误差阈值内优化的功耗有限. 反之, 在FPRM形式下, 电路sym10和pcle存在部分乘积项,这些乘积项与其他乘积项交叠程度不大, 而对应的信号密度比较大. 因此, 通过删除这些乘积项,在减少总的信号跳变密度的同时又能较好地控制错误率的增加, 从而得到较好的优化效果.

本文提出的算法可以处理输入为85个变量的大电路, 其关键原因在于无论是RM逻辑的极性搜索还是RM函数的错误率求解, 均基于乘积项, 而不是最小项. 因此, 待处理电路的乘积项的数量会影响算法的运行时间. 此外, 考虑到逻辑函数的乘积项数量与输入变量的数量无关, 所以本文算法可以实现大函数的FPRM的功耗优化.

5 结论

本文提出了一种基于近似计算技术的RM逻辑功耗优化算法, 该算法利用遗传算法, 结合提出的以信号概率和跳变密度为参数的RM函数动态功耗数学模型和以功耗优化为导向的极性搜索, 得到功耗优化后的FPRM表达式, 然后利用提出的基于双锐积运算的RM函数的错误率计算方法, 通过有选择性地删除某些FPRM乘积项, 实现在错误率约束下的FPRM逻辑的功耗优化. 提出的优化算法用MCNC电路进行了测试, 在平均错误率约束为3.21％时, 测试电路功耗的平均功耗减少了22.77％.

[1] Shin D, Gupta S K. Approximate logic synthesis for error tolerant applications[C]//Design, Automation & Test in Europe Conference & Exhibition, 2010:957-960.

[2] Zou C, Qian W, Han J. DPALS: A dynamic programming-based algorithm for two-level approximate logic synthesis[C]//IEEE 11th International Conference on ASIC, 2015:1-4.

[3] Ichihara H, Inaoka T, Iwagaki T, et al. Logic simplification by minterm complement for error tolerant application[C]//33rd IEEE International Conference on Computer Design, 2015:94-100.

[4] Miao J, Gerstlauer A, Orshansky M. Multi-level approximate logic synthesis under general error constraints[C]//IEEE ACM International Conference on Computer-Aided Design, 2014:504-510.

[5] Wu Y, Qian W K. An efficient method for multi-level approximate logic synthesis under error rate constraint [C]//Proceedings of the 53rd Annual Design Automation Conference. New York, USA: ACM Press, 2016:1-6.

[6] Bernasconi A, Ciriani V. 2-spp approximate synthesis for error tolerant applications[C]//17th Euromicro Con- ference on Digital System Design, 2014:411-418.

[7] Soeken M, Große D, Chandrasekharan A, et al. BDD minimization for approximate computing[C]//21st Asia and South Pacific Design Automation Conference, 2016: 474-479.

[8] Mozammel H A K. Design of reversible synchronous sequential circuits using pseudo reed-muller expressions [J]. IEEE Transactions on Very Large Scale Integration Systems, 2014, 22(11):2278-2286.

[9] 尹浩凯, 马雪娇, 夏银水. 基于近似逻辑的不完全指定FPRM函数的功耗优化[J]. 宁波大学学报(理工版), 2019, 32(3):28-34.

[10] 俞海珍, 汪鹏君, 张会红, 等. 基于三值多样性粒子群算法的MPRM电路综合优化[J]. 电子学报, 2017, 45(7): 1601-1607.

[11] Wang X, Lu Y, Zhang Y, et al. Probabilistic modeling during power estimation for mixed polarity reed-muller logic circuits[C]//Green Computing & Communications, IEEE, 2013:1414-1418.

[12] 瞿婷, 王伦耀, 罗文强, 等. 大函数ISFPRM面积优化方法[J]. 电子学报, 2018, 46(5):1101-1106.

[13] Liang J, Han J, Lombardi F. New metrics for the reliability of approximate and probabilistic adders[J]. IEEE Transactions on Computers, 2013, 62(9):1760- 1771.

[14] Miao J, Gerstlauer A, Orshansky M. Approximate logic synthesis under general error magnitude and frequency constraints[C]//Proceedings of the International Con- ference on Computer-Aided Design, 2013:779-786.

[15] 王伦耀, 夏银水, 陈偕雄. 逻辑函数的双逻辑综合与优化[J]. 计算机辅助设计与图形学学报, 2012, 24(7): 961-967.

[16] 王伦耀, 夏银水, 陈偕雄, 等. 基于不相交乘积项的逻辑探测和拆分算法[J]. 电子学报, 2012, 40(10):2091- 2096.

[17] 王玉花, 王伦耀, 夏银水. 基于不相交项并行列表技术的FPRM实现[J]. 电子与信息学报, 2014, 36(9):2258- 2264.

Power optimization for FPRM logic using approximate computing technique

WANG Yichen, WANG Lunyao*, XIA Yinshui, CHU Zhufei

( Faculty of Electrical Engineering and Computer Science, Ningbo University, Ningbo 315211, China )

A power optimization algorithm based on approximate computing technique is proposed for FPRM logic circuits. The algorithm includes FPRM logic circuits dynamic power estimation model based on signal probability and transition density, a genetic algorithm for RM logic power optimization using polarity searching, and the error rate calculation for RM logic using double sharp product operation. Under the constraint of error rate, some product terms are selectively deleted to reduce power consumption. The proposed algorithm is implemented in C programming language and tested under MCNC benchmarks. The experimental results show that using the approximate computing technique presented in this work, the average dynamic power can be reduced by 22.77％ with the average error rate of 3.21％.

approximate computation; error rate; polarity searching; power consumption optimization

TN47; TP391

A

1001-5132（2020）01-0045-06

2019−05−28.

宁波大学学报（理工版）网址: http://journallg.nbu.edu.cn/

国家自然科学基金（U1709218, 61871242）; 浙江省自然科学基金（LY19F040004）; 宁波市自然科学基金（2019A610077）.

王一琛（1993－）, 女, 浙江舟山人, 在读硕士研究生, 主要研究方向: 逻辑综合与优化. E-mail: 543746091@qq.com

王伦耀（1972－）, 男, 浙江宁波人, 教授, 主要研究方向: 逻辑综合与优化. E-mail: wanglunyao@nbu.edu.cn

（责任编辑 史小丽）