混合变分自编码
2020-01-09陈亚瑞蒋硕然杨巨成赵婷婷张传雷
陈亚瑞 蒋硕然 杨巨成 赵婷婷 张传雷
(天津科技大学计算机科学与信息工程学院 天津 300457)
近几年,深度学习成为人工智能领域的研究热点,概率生成模型是构建深层模型的基本结构之一,也是进行知识表示的重要方法[1-2].概率生成模型通过对隐变量层结构进行学习,学习数据的内部结构关系,发现数据内的因果关系,实现数据的表示[3-4].生成模型中隐变量及模型参数的后验概率分布一般是难解,对于生成模型如何进行有效的推理和学习,计算隐变量及参数的后验概率分布是一项重要的研究内容[4-6].变分推理是近似求解隐变量及模型参数后验概率分布的方法之一[5].传统变分推理在处理生成模型(如混合高斯模型)时,要求近似后验概率有解析表示形式,即要求隐变量或模型参数具有共轭先验分布形式,但该方法对处理一般隐变量结构的生成模型存在困难[5,7].变分自编码(variational auto-encoder, VAE)模型是一种基于连续隐向量的生成模型,它结合了变分方法和神经网络,常被用于构建深度生成模型(deep generative model, DGM)[1,7-8].
VAE模型通过引入近似后验概率,利用变分转换给出边缘似然的变分下界,再通过求解该优化式给出隐变量近似后验概率分布[7-9].VAE中的生成模型及识别模型均采用多层神经网络结构,在求解优化问题时,首先对边缘似然的变分下界进行重参化(reparameterization)处理[10],得到该下界的一个可微无偏估计——随机梯度变分贝叶斯估计(stochastic gradient variational Bayesian estimator, SGVB),此时采用标准的随机梯度下降方法可以进行推理和学习[9].对于生成模型是非线性神经网络的模型,SGVB也可以通过随机梯度下降方法方便求解[11-14].VAE的推理模型也称为概率编码部分可以用于识别、去噪、数据表示和可视化等方面,VAE的识别模型也称为概率解码部分可以用于生成数据等[1,7-8].
对于VAE模型,如何解决其中的自截枝问题、对于传统的非监督学习方法如何再加入标签信息、如何提高模型的泛化能力以避免模式崩溃,针对这些问题研究者开展了很多相关的研究工作.
针对VAE方法中的模型过截枝问题,斯坦福Yeung等人[15]提出epitomic variational autoencoder模型,该模型由几个稀疏的变分自编码(每一个稀疏的变分自编码称为一个缩影)组合而成,稀疏模型之间通过共享自编码结构来提高模型的泛化性.伦敦大学帝国理工学院的Dilokthanakul等人[16]提出高斯混合变分自编码(Gaussian mixture variational autoencoder, GM-VAE)模型,通过引入高斯混合模型作为隐变量的先验分布,并利用GM-VAE构建深度生成模型实现无监督聚类.但是该方法对仍旧存在严重的过正则化问题.Kingma等人[17]将可逆自回归流(inverse autoregressive flow, IAF)策略应用于变分自编码模型(VAE-IAF),该方法利用一系列可逆函数逐步迭代构建出变分后验概率分布,其中的可逆函数由自回归神经网络构成.该方法给出了更灵活方便的变分后验概率分布结构,更有利于处理高维隐空间,但是自回归网络打乱了隐变量空间的分布.Sohn等人[18]提出一种条件变分自编码(conditional variational autoencoder, CVAE)模型使得解码器不仅可以生成新的样本(如手写字体),而且可以生成指定的样本(如某个手写字体).该方法通过在生成模型和识别模型的神经网络结构中分别加入了标签信息作为条件变量,再利用随机梯度下降方法求解优化问题,该结构丰富了隐变量结构.但是无监督学习在训练离散指示变量时产生的错误标记会直接影响生成模型的性能.Nalisnick等人[19]提出变分自编码的非参数形式——折棍变分自编码(stick-breaking variational autoencoder, SB-VAE)模型.该模型引入有限随机过程[20-21]作为隐变量先验分布,并采用随机梯度变分贝叶斯方法进行后验推理,计算折棍参数.
已有的相关研究中,变分自编码中的变分识别模型大都假设多维隐变量之间是相互独立的,这种假设简化了推理过程,但是这使得变分下界过于松弛,同时忽视了隐变量之间的相互影响及其对输出样本的影响,限制了隐变量空间的表示能力.已有的VAE改进算法大多集中于对隐变量增加先验分布或加入标签信息到模型中进行监督学习或半监督学习.
本文提出混合变分自编码(mixture of variational autoencoder, MVAE)模型,以变分自编码作为混合模型的基本组件.该模型以连续隐向量作为模型的隐层表示,其先验分布为高斯分布;以离散隐向量作为组件的指示向量,其先验分布为多项式分布.对于MVAE模型的变分优化目标,本文采用重参策略和折棍参数化策略处理目标函数,并用随机梯度下降方法求解模型参数.
1 变分自编码
变分自编码是结合了变分贝叶斯方法和神经网络结构的生成模型.其中采用变分方法将变量求和的推理问题转化为优化问题;相比传统的共轭先验分布,采用神经网络近似后验分布扩展了算法的应用范围.
对于生成模型p(x,z)=p(z)p(x|z),其中x表示观测向量,z表示隐向量,p(z)表示隐向量先验概率分布,p(x|z)表示条件概率分布.观测样本x的生成过程:
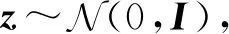
x|z~p(x|z).
生成模型中概率推理问题是根据观测数据集X={x(1),x(2),…,x(N)},求解数据集的边缘似然p(X)及隐向量后验概率分布p(z|x),即
(1)

(2)
式(1)和式(2)所示的概率推理问题都是难解的,故采用近似方法进行近似求解,变分技术是一种重要的确定性近似推理方法.
样本点x(i)的对数边缘似然lnp(x(i))的变分表示形式为
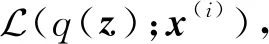
(3)
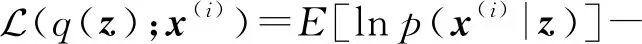
(4)

此时求解样本边缘概率分布的概率推理问题转化为下面的优化问题:
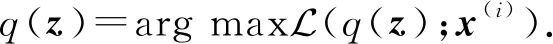
(5)
求解优化式(5)给出对数边缘似然lnp(x(i))的下界,同时自由分布q(z)是后验概率分布p(z|x(i))的近似分布,即q(z)≈p(z|x(i)).
变分自编码模型中,q(z)及p(x|z)都是由神经网络构成,可以通过随机梯度下降方法和BP算法求解式(5).
2 混合变分自编码
本文提出混合变分自编码模型,它通过多个变分自编码组件生成样本数据.该模型以连续隐向量作为模型的隐层表示,其先验分布为高斯分布;以离散隐向量作为组件的指示向量,其先验分布为多项式分布.
2.1 生成模型
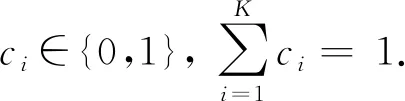
(6)
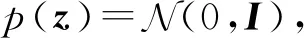
(7)
(8)
其中,p(c)表示隐向量c的先验分布,K是一个常量,表示混合组件的个数,π={π1,π2,…,πK}表示多项式分布参数集合,p(z)表示隐向量z的先验分布,θ={θ1,θ2,…,θK}表示条件概率分布的参数集合.当观测向量x是连续值时,条件概率分布pθk(x|z)为基于神经网路的高斯分布;当向量x是离散值时,pθk(x|z)为基于神经网络的多元伯努利分布.生成模型的联合概率分布形式为
p(x,z,c)=p(z)p(c)p(x|z,c).
混合变分自编码生成模型如图1所示:
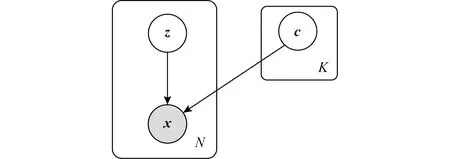
Fig. 1 Mixture variational autoencoder图1 混合变分自编码模型
2.2 变分下界
混合变分自编码模型中的关键问题是根据观测数据计算模型参数及隐变量后验概率分布.直接利用EM算法求解是难解的,此时采用变分方法进行近似求解.
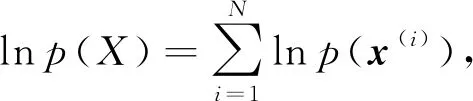
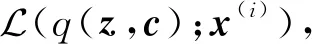
(9)

(10)
其中,q(z,c)为自由分布,也是向量z,c的近似后验概率分布.因为q(z,c)与p(z,c|x(i))之间的KL散度度量是非负的,即DKL(q(z,c)‖p(z,c|x(i)))≥0,故
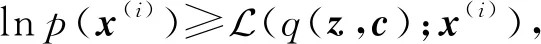
(11)
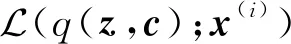
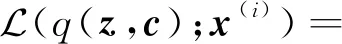
(12)
在混合变分自编码模型中,条件概率分布pθk(x|z)及自由分布qφ(z),qη(c)均是基于神经网络结构.具体为
1) 对于生成模型.若向量x为离散值,则条件概率分布pθk(x|z)为基于神经网络的伯努利分布,即
pθk(x|z)=B(x;μ(z;θk)),
(13)
其中μ(·;θk)由基于参数θk的神经网络实现.具体地,神经网络结构实现为
μ(z;θk)=sigmoid(W2tanh(W1z+b1)+b2),
(14)
该神经网络结构中,条件概率分布pθk(x|z)中θk的具体形式为θk={W1,b1,W2,b2}.激活函数sigmoid()与tanh()的操作是对向量元素操作.
若向量x为连续值,则条件概率分布pθk(x|z)为基于神经网络的高斯分布,即
pθk(x|z)=N(x;μ(z;θk),diag(σ2(z;θk))),
(15)
其中μ(·;θk),σ2(·;θk)分别由基于参数θk的神经网络实现.具体地,神经网络结构实现为
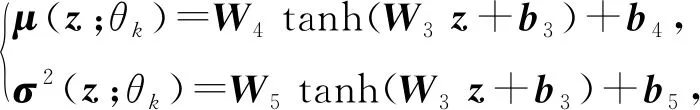
(16)
该神经网络结构中,模型参数θk的具体形式为
θk={W3,b3,W4,b4,W5,b5}.
2) 对于自由分布qφ(z).隐变量z为连续向量,自由分布qφ(z)为基于神经网络的高斯分布,即
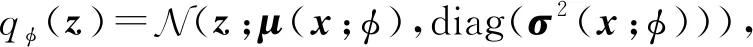
(17)
其中μ(·;φ),σ(·;φ)分别由基于参数φ的神经网络实现.神经网络具体形式类似于式(16)所示.
3)对于自由分布qη(c).隐变量c为多项式变量,自由分布qη(c)是多项式分布,即
(18)
其中,qη(c1=1)=π1(z;η1),πk(·;ηk)表示由基于参数ηk的神经网络实现.神经网络具体形式类似于式(14)所示.
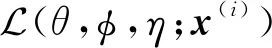
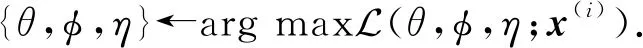
(19)
3 优化问题求解
为了求解变分优化式(19),首先采用重参策略(reparameterization trick)采样z(i)和c(i),然后再利用随机梯度下降方法进行参数更新.
利用后验概率分布qφ(z),如式(17)所示,根据观测样本x(i)采样z(i,l),即
z(i,l)=μ(i)+σ2(i)⊙ε(l),
(20)
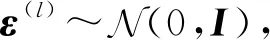
(21)
其中符号⊙表示点乘运算.根据重参策略,函数的期望可以通过采样方法计算,即
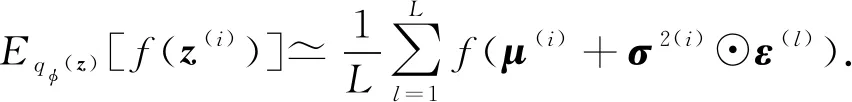
(22)
进一步,利用后验概率分布qη(c),如式(18)所示,根据折棍参数化策略(stick-breaking parame-terization),从后验概率分布qη(c)中采样c(i),即
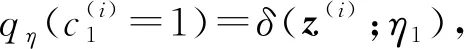
(23)
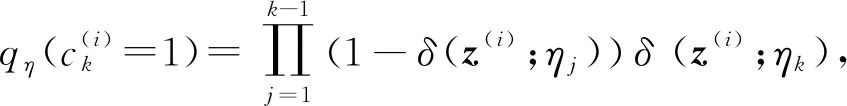
(24)
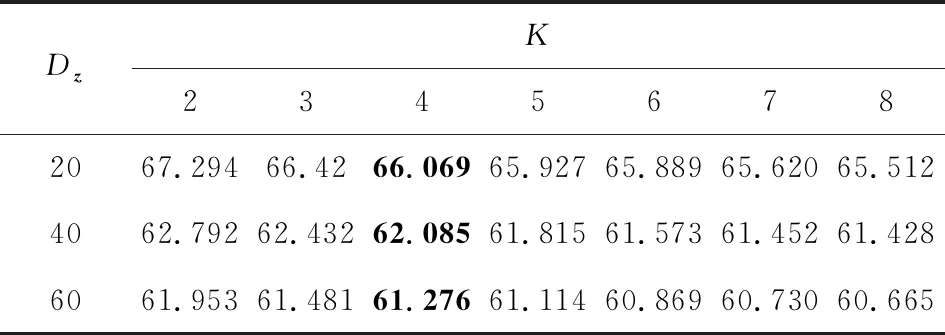
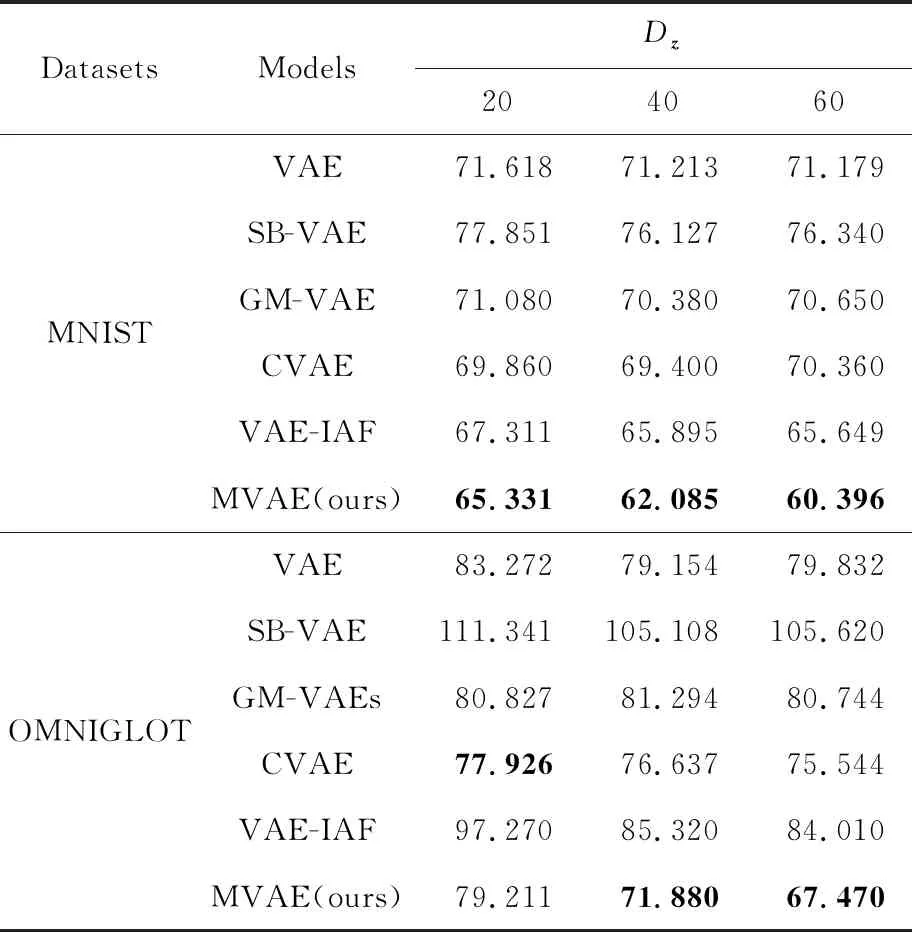
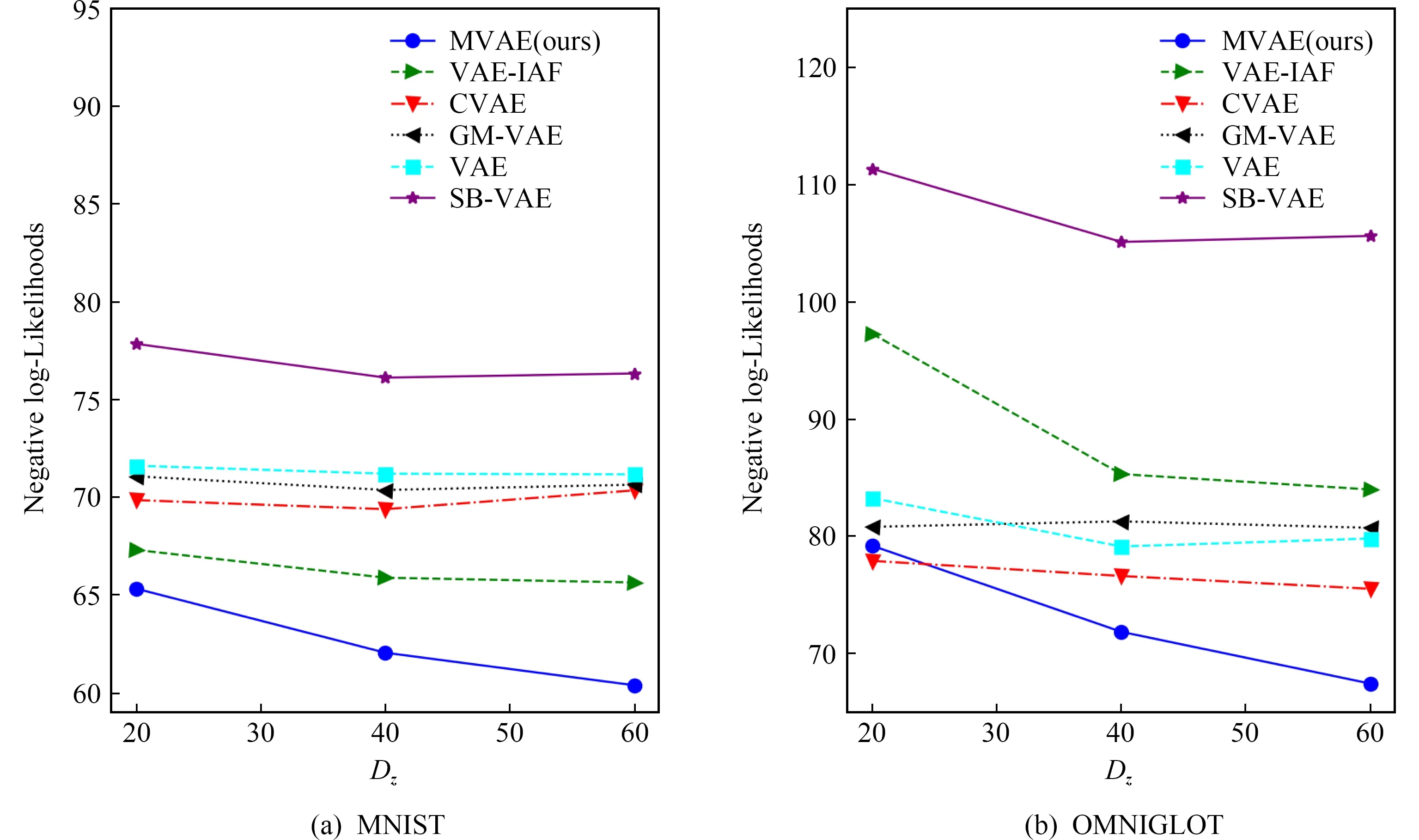
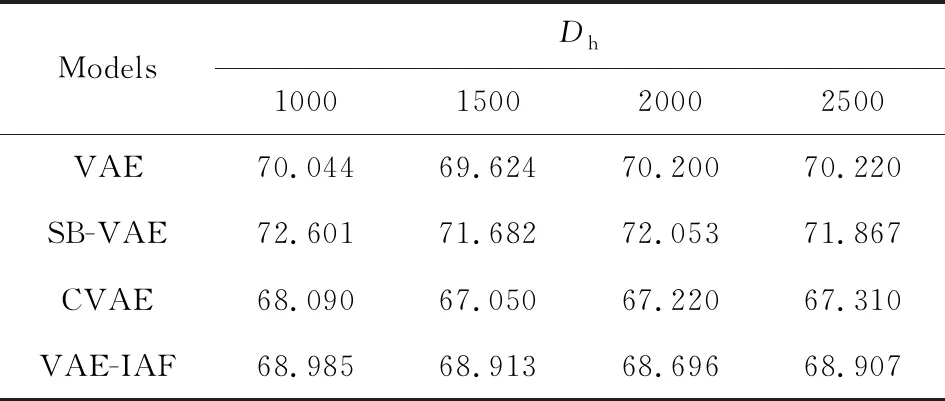
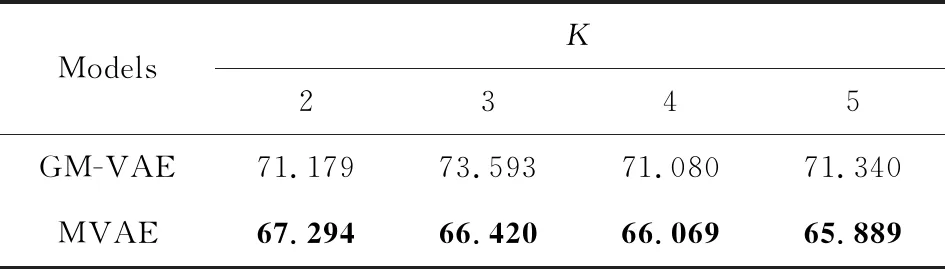
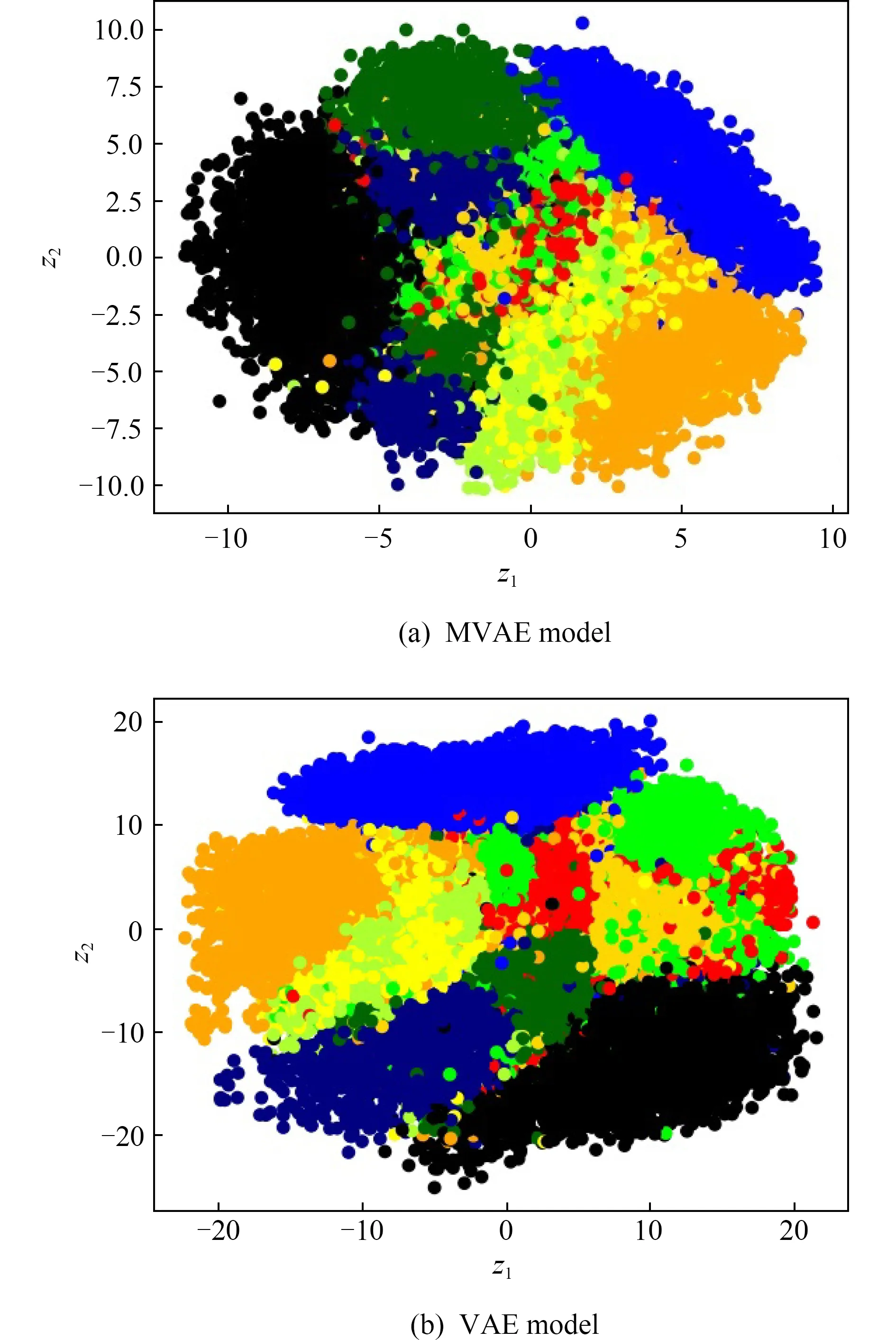
1 (25) 此时,多项式隐变量c(i)的采样结果为 (26) 根据采样的数据z(i,l)和c(i),数据点x(i)的对数边缘下界为 (27) 对于数据集X={x(1),x(2),…,x(N)},采用批处理方法构建数据集边缘概率分布,从数据集X中随机选取批处理样本集XM={x(1),x(2),…,x(M)}.Kingma和Welling[7]证明当批处理规模M足够大时,重采样过程中采样规模L值可以设定为L=1,本文中我们将重采样中的采样规模L=1.利用批处理方式,数据集X的边缘概率分布下界为 (28) 对边缘概率分布下界(式(28))求导,采用梯度下降方法更新模型参数.算法的表示如算法1所示: 算法1.混合变分自编码算法. 输入:数据集X,数据集规模M=500,L=1; 输出:模型{θ,φ,η}. θ,φ,η←初始化参数; repeat: XM←从数据集X中随机抽取数据子集; g←θ,φ,η计算目标函数梯度; θ,φ,η←利用梯度g,采用随机梯度下降方法更新参数; until参数(θ,φ,η)收敛; return参数θ,φ,η. 本节设计对比实验验证MVAE在对数似然下界及隐变量空间上的性能.具体包括3个实验:实验1,通过对比实验确定MVAE模型的参数K;实验2,设计不同模型的对数似然下界对比实验,以及不同神经网络结构下对数似然下界对比试验;实验3,对比MVAE算法和VAE算法在隐层表示空间的表示能力. 本实验采用的数据集包括MNIST数据集[22]和OMNIGLOT数据集[23].具体地,MNIST是标准手写数字数据集,包含60 000个样本的标准手写数字,其中每个样本是一张28×28的灰度图片.OMNIGLOT是手写字符数据集,包含50种不同语言中的1 623个不同手写字符,共有24 345个样本,其中每个样本也是一张28×28灰度图片. 对比实验模型包括:MVAE,VAE,CVAE,VAE-IAF,GM-VAE,SB-VAE,算法详细信息如表1所示.在所有的模型中,识别模型(或变分模型)和生成模型均采用双隐层的全连接神经网络实现,并且训练时的批量样本大小为M=500,迭代次数为epochs=200,学习率为0.001. Table 1 Detailed Information of Comparison Models表1 对比模型详细信息 对于MVAE模型,我们在MNIST数据集上,通过设置不同的子模型个数K和隐变量维度Dz,分别计算相应的对数似然的下界,通过分析确定子模型个数K.具体地,分别设置子模型个数K=2,3,…,8,同时设置隐变量z的维度分别为Dz=20,40,60.变分模型qφ(z|x),qη(c|z)和每个生成子模型pθk(x|z)都是双隐层的全连接神经网络,每个隐含层包含500个激活函数为tanh的神经元. MVAE模型在不同参数下给出的负对数似然(negative log-likelihoods, NLL),如表2所示.从表2可以看到,随着生成子模型个数K的增加,MVAE在不同隐向量维度Dz下对数似然的下界都在提高,并且当生成子模型个数K≥4时逐步达到稳定. Table 2 The Comparison of the Negative Log-Likelihoods on the MNIST Dataset表2 在MNIST数据集上负对数似然下界结果对比 Notes: The optimal results are in bold. Fig. 2 The comparison of hidden spaces of MVAEwith different parameters K图2 K不同时MVAE模型的隐变量空间生成样本比较 为了进一步分析不同参数K设置下对隐变量空间的影响,我们设置隐变量的维度Dz=2,子模型的个数K分别取值为2,3,4,5,利用MNIST数据集训练相应的MVAE模型.然后分别利用相应MVAE模型的生成模型生成手写字体数据,相应隐向量空间生成样本情况如图2所示.图2中,生成的不清楚的数字在图中分别用方框标出.可以看出,生成的手写数字随着生成子模型个数K的增加图片变得越来越清晰.同时当子模型个数达到K=4时,模糊的生成图片数量最少. 通过实验分析,对于MVAE模型,最优的生成子模型个数为K=4,在4.2~4.4节的实验中默认设置MVAE模型参数K=4. 本节在MNIST和OMNIGLOT数据集上,对比MVAE模型与VAE,GM-VAE,VAE-IAF,CVAE,SB-VAE模型的负对数似然.本实验中,VAE,GM-VAE,VAE-IAF,CVAE,SB-VAE中的生成模型和识别模型分别采用2个隐层的神经网络,其中每个隐层有500个隐节点,采用tanh激活函数.MVAE,GM-VAE模型中的参数K=4,每个子模型都采用与VAE中生成模型相同的神经网络结构.负对数似然函数实验对比结果如表3和图3所示: Table 3 Comparison of the Negative Log-Likelihoods on Two Datasets表3 2个数据集上不同模型的负对数似然下界比较 Note: The optimal results are in bold. Fig. 3 The comparison of the negative log-likelihoods of different models on the MNIST and OMNIGLOT datasets图3 在数据集MNIST和OMNIGLOT上不同模型给出的负对数似然下界比较 分析表3和图3可知,对于MNIST数据集,在隐变量z不同维度Dz分别取值20,40,60的情况下,MVAE方法给出的负对数似然值最小,即MVAE模型给出的对数似然下界最紧致.对于该数据集,模型在负对数似然值上的表现从优到差的顺序依次是:MVAE>VAE-IAF>CVAE>GM-VAE>VAE>SB-VAE.对于OMNIGLOT数据集,CVAE模型在维度Dz=20上给出了最优的负对数似然值,MVAE模型在维度Dz=40,60上给出了最优的负对数似然值.随着隐变量维度的增加,相比于CVAE模型,MVAE模型给出的对数似然下界变得更紧致.对于该数据集,模型在负对数似然值上的综合表现从优到差的顺序依次是:MVAE>CVAE>VAE>GM-VAE>VAE-IAF>SB-VAE. 同时随着隐向量维度Dz的增加,MVAE模型的负对数似然值越来越小,即MVAE模型随着隐向量维度的增加,给出的对数似然下界明显越来越紧致.而对于模型VAE-IAF,CVAE,GM-VAE,VAE,SB-VAE,当模型维度 从40变成60时,负对数似然值变化较小. 通过实验分析可知,对于MNIST和OMNIGLOT数据集,MVAE模型给出了更紧致的对数似然下界,同时随着隐变量维度的增加,对数似然下界明显越来越紧致,这表示MVAE模型在推理过程中给出了更优的结果. 由4.2节实验可知MVAE模型具有更优的推理性能,MVAE是通过多个子模型更灵活的生成模型结构提高了推理性能,而不是简单地扩展神经网络的隐层神经元个数.为了说明这一点,本实验将SB-VAE,VAE,CVAE,VAE-IAF生成模型中神经网络的2个隐层分别扩展到Dh=1 000,1 500,2 000,2 500,实验结果如表4所示.MVAE和GM-VAE都是有子模型结构的,本实验将MVAE和GM-VAE模型的2个隐层的神经元个数均设定为Dh=500,同时生成子模型个数分别设为K=2,3,4,5.在MNIST数据集上,对于上述参数设置,分别计算相应的负对数似然值,实验结果如表5所示: Table 4 Comparison of the Negative Log-Likelihoods with Different Neural Network Structures on the MNIST表4 数据集MNIST的不同神经网络结构下 负对数似然结果对比 Table 5 Comparison of the Negative Log-Likelihoods with Different Structures on the MNIST when DA=500 Notes: The optimal results are in bold. 表4显示,VAE,SB-VAE,CVAE,VAE-IAF模型的对数似然下界并没有随着神经网络隐层节点个数的增加而明显提高.由表5可知,在大致相同神经网络结构的情况下,MVAE模型给出了负对数似然值最小,即MVAE模型给出的对数似然的下界最紧致.同时随着参数K的增加,2个模型对数似然下界越来紧致并逐步稳定. 综上所述,MVAE模型与不同神经网络结构相比,在不同数据集上,均具有最紧致的对数似然下界.实验结果表示MVAE模型通过灵活的生成模型结构,有效提高了变分近似推理的性能. Fig. 4 Comparison of latent variable spaces oftwo models on the MNIST图4 在MNIST数据集上2个模型的隐变量空间对比 本节在MNIST数据集上通过对隐变量空间可视化,对比MVAE和VAE模型隐变量空间生成样本的情况.实验中,对于MVAE模型,设定参数K=4,对于MVAE和VAE模型,分别设定隐变量z的维度Dz=2,生成模型及识别模型中的神经网络隐层节点Dh=500.对于MVAE和VAE模型,在隐变量区域进行采样,生成相同样本的区域标注同一种颜色,生成不同样本的区域标注不同的颜色.最终MAVE模型和VAE模型的二维隐变量空间生成样本情况如图4所示. 根据实验结果图4可知,VAE模型中隐变量空间的每个维度的取值区间为(-10,10),而MVAE模型中隐变量空间的每个维度的取值区间为(-20,20).很明显,MVAE模型有效扩大了隐变量空间的表示范围.同时根据图4结果可以看出,相比VAE模型,MVAE模型的隐变量空间更具有可分性,有效解决了VAE模型中存在的模式崩塌问题.该实验结果表明,MVAE模型的隐变量空间具有更丰富的表示能力. 本文提出一种混合变分自编码模型,采用指示变量将多个生成模型组件组合到一起,利用变分近似构建目标函数,并采用重参技术及折棍参数化策略求解优化问题.该模型采用连续型高斯隐变量作为隐层表示,采用离散型多项式隐变量作为组件的指示变量.理论分析和试验结果表示,MVAE模型中丰富的生成模型结构有效提高了数据对数似然的下界,生成模型的混合组件方式增强了隐变量空间的表示能力.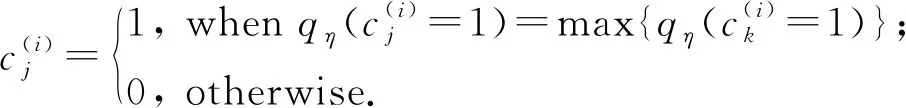
4 对比实验与结果分析

4.1 确定子模型个数

4.2 对数似然下界对比实验
4.3 不同神经网络结构下对数似然下界对比实验
4.4 隐变量空间表示能力对比
5 总 结
