大规模拼车算法研究进展
2020-01-09童咏昕
徐 毅 童咏昕 李 未
(软件开发环境国家重点实验室(北京航空航天大学) 北京 100191) (北京航空航天大学计算机学院 北京 100191)
拼车,也即“合乘”、“共乘”和“顺风车”,是指多位拥有不同起终点位置的乘客经协商共同乘坐同一辆车并分担费用的共享出行模式.拼车因其社会和经济价值而得到了广泛应用,也逐渐由原先熟人间的小范围共乘变为如今市民间的大规模拼车.当下越来越多的共享出行平台推出拼车服务,例如滴滴出行公司的拼车业务、Uber公司的UberPool业务和ExpressPool业务、Lyft公司的Lyft Line业务、Waze公司的Waze Carpool业务等[1-5].同时,拼车的参与规模也呈爆发式增长.据统计,2016年滴滴出行公司的拼车业务覆盖全国超过300个城市,日均订单量超过157万.
较之拼车而言,另一种传统的共享出行模式为出租车,俗称打车,即乘客临时雇佣汽车并按里程付费的出行模式.在出租车模式中,每位司机在同一时间段内最多服务于单一订单.而在拼车模式中,每位司机在同一时间段内可服务于多个行程间有重叠的订单.正是二者服务模式的差异,导致其核心算法模型有着本质区别.具体而言,打车模式聚焦于每个订单与每位司机之间的匹配满意度,因此其算法原型为二分图匹配;而拼车模式更关心各订单之间协作的满意度,并通过合理的路线规划来优化所有订单与司机间的满意度,其本质算法模型为拨号叫车问题(dial-a-ride problem, DARP),即为1个司机规划1条路线来完成由多个乘客发出的运送请求从而最小化总行驶距离的问题[6].特别是,从问题的计算复杂性分析视角可见,适用于打车模式的二分图匹配问题在多项式时间内可求得最优解,而DARP属于NP-难问题[6].因此,求解拼车问题即使在小规模静态场景中也具有相当的难度与挑战.
近年来,移动互联网与普适计算技术日益普及,给拼车问题带来了数据量大、动态性强、目标多样、应用范围广的新特点.在此背景下,拼车问题也逐渐演变为大规模拼车问题.例如在2017年,滴滴出行公司的拼车业务累计分享座位数达到10.5亿个,涉及到的数据规模庞大.此外,在拼车需求高峰时段每秒就有可能产生上百个拼车订单,平台需要在秒级时间内做出响应,数据产生的动态性强.同时,大规模拼车问题中平台、司机和乘客等各参与方都有各自的目标:平台期望更高的收益,司机期望更多的接单量,而乘客则期望更高效的出行时间,因此求解大规模拼车问题还需考虑目标的多样性.最后,拼车问题还具有广泛的应用,衍生出如送餐、最后一公里配送等一系列变种应用.上述这些新挑战导致原本针对小规模应用的拼车算法失效,求解大规模拼车问题的难度上升,因而催生了大量针对大规模拼车问题的新理论、算法、优化与实现的学术研究.同时,为实现产品级拼车应用,激励机制、隐私保护、人身安全保障等关于社会影响因素的实际问题也是大规模拼车问题的相关研究热点.
本文总结近年来大规模拼车算法的最新研究进展,做出了3点贡献:
1) 重点回顾了当前大规模拼车平台的核心算法问题——路线规划问题,并从偏好角度、优化目标、业务场景、时间复杂性、近似理论分析等多个维度对相关算法研究进行了系统性的分析和比较;
2) 对实际拼车应用驱动的一系列社会影响因素(如激励机制、隐私保护和人身安全保障等)的研究进展进行了详细的阐述和讨论;
3) 结合现有研究的不足之处,展望了拼车技术的未来潜在研究方向,为相关科研人员和从业者提供了有价值的参考.
1 拼车问题概述
本节首先介绍拼车问题涉及的基本概念与定义,随后介绍本综述与现有相关综述的区别,最后介绍大规模拼车平台的通用工作流程.
1.1 问题定义介绍
首先介绍拼车问题涉及的3个基本概念,即司机、订单与平台.
定义1.司机.拼车问题中的1位司机用w表示,它包含司机的初始位置、汽车容量等属性.1个由m位司机组成的集合表示为W={w1,w2,…,wm}.
定义2.订单.拼车问题中的1个订单用r表示.乘客向平台提交拼车请求(也称为发布请求),平台收到请求并生成1个完整的订单.1个订单包含的属性有:请求的发布时间、乘客的起点(即上车地点)、乘客的终点(即下车地点)、截止时间与乘客数量.1个由n个订单组成的集合表示为R={r1,r2,…,rn}.
在拼车问题中,如果1个订单在发布后被司机接受,且在其截止时间之前司机将乘客送达其终点,则称为司机完成了该订单.司机w被指派的订单用集合Rw表示.
定义3.平台.拼车问题中的平台用P表示,其拥有一定数量的司机(来自司机集合W,同时收到一系列订单(来自订单集合R).平台将订单分配给司机,为司机规划行驶路线,并最终通过司机完成的订单获取收益.
根据定义1~3,下文介绍拼车的核心问题,即路线规划问题.
定义4.路线.给定司机w与其被指派的订单集合Rw.司机w的路线Sw定义为由w的起始位置与订单的起点或终点构成的1个序列,即Sw={l0,l1,…,lk}.其中,l0是司机w的起始位置,l1,…,lk是集合Rw中某个订单的起点或终点.
在实际应用和现有文献中,一条可行的路线还需要满足一定约束条件,这些约束条件通常包括:
1) 顺序约束.在一条可行路线中,任意订单的起点应该出现在它的终点之前,即司机需要先行驶至起点接取乘客、再行驶至终点送达乘客.
2) 容量约束.在任意时刻,每位司机乘载的乘客总人数不得超过该辆汽车的容量.
3) 截止时间约束.每位乘客需要在其订单的截止时间之前被送达至终点.
4) 不可撤回约束.一旦平台指派并通知某个司机完成某个订单,则该指派决定不可撤回.
5) 绕路约束.在一条可行路线中,每位乘客的绕路距离不超过某个阈值.这里绕路距离等于乘客由于参与拼车而多绕行的距离.
基于定义1~4,一个通用的路线规划问题见定义5.
定义5.路线规划.在拼车问题中,给定司机集合W、订单集合R和平台P.路线规划问题旨在为每位司机w∈W决定一条满足某些约束条件的行驶路线Sw,并使得某个优化目标达到最优.
在现有研究中,不同的偏好角度往往决定了不同的优化目标.例如,基于司机角度的优化目标包括最小化司机的行驶总距离、最小化司机的最大完工时间;基于乘客角度的优化目标包括最小化乘客的等待时间、最大化乘客的社会效用;基于平台角度的优化目标包括最大化平台的订单完成数以及最大化平台的总收入等.除这些优化目标外,文献[7]还提出了1个灵活、泛化的目标函数.通过调节合适的参数,该目标函数可以等价地转换为不同偏好角度的优化目标.第2节将对与路线规划相关的文献进行具体地分析和总结.
1.2 现存综述区别
拼车问题的算法原型可追溯到拨号叫车问题.现存关于拼车算法的综述可分为2类:拨号叫车问题的综述和拼车技术综述,下面将进一步阐述本文与此2类现存工作区别.
1.2.1 与拨号叫车问题综述的区别
拨号叫车问题是运筹学研究中的一个经典的算法理论问题,已有一些运筹学领域研究对求解该问题的相关算法进行了总结[6-12].其中,综述性文献[7-12]均发表于2013年之前,并没有系统地讨论近年来的拼车算法的相关文献.而近期的综述性文献[6]对基于拼车出行的拨号拼车问题进行了系统性的总结,该文献主要讨论理论层面的拼车路线规划问题,而没有考虑在真实应用场景中大规模拼车所面临的实际问题,如路网结构、时空索引设计等,同时还缺少对拼车出行中如激励机制、隐私保护等其他社会影响因素的系统性讨论.
1.2.2 与拼车技术综述的区别
现存关于拼车技术的系统性文献综述十分有限,仅有文献[13].与文献[13]相比,本文的主要区别与创新之处在于3点:
1) 文献[13]覆盖的文章多发表于2015年之前,滴滴出行、Uber等平台刚刚推出自己的拼车应用,拼车发展尚在萌芽阶段,其未能囊括近4年来飞速发展的拼车新技术;而本文则关注近年来大规模拼车所具有的数据量大、动态性强、目标多样、应用范围广等新特性,总结了近4年新的相关论文以及核心技术的改进,更具有时效性与全面性.
2) 文献[13]侧重于介绍一般化的拼车概念,因此基于简单的司机乘客数量对拼车问题进行了分类,在算法上也仅仅介绍了Filter and Refine这一种拼车框架;而本文更注重拼车算法的研究,根据平台角度、司机角度和乘客角度下的不同优化目标对大量拼车算法的研究文献进行了更深层次的分类、算法分析与对比,更具有深度性.
3) 文献[13]在介绍拼车的社会影响因素时内容较为简单宽泛;而本文针对每个社会影响因素调研了更全面的相关工作,并进行了细致的分类与对比,更具有系统性.
1.3 平台工作流程
拼车服务中的用户主要由司机和乘客组成,他们通过拼车平台建立联系,分别构成这一双边市场的供给与需求.典型的大规模拼车平台有Uber、滴滴出行、Lyft、Grab、Via与Waze CarPool等[1-2,5,14-16].
如图 1所示,大规模拼车平台(简称“平台”)包含两大主要模块,即路线规划与社会影响因素的相关解决方案(包括激励机制、隐私保护与人身安全保障3个子模块),在这些模块作用下,平台通过司机与乘客的手机客户端对二者进行管理和分配.具体的工作流程有3个:
1) 提交订单.提交订单阶段指的是乘客发起请求到平台接受该请求的过程.在这个阶段中,乘客提出一个拼车请求.平台分别调用隐私保护与激励机制模块,首先通过隐私保护机制保护乘客的敏感信息(如位置信息),并通过激励机制对该请求进行定价.随后,平台将价格等信息发送给乘客,待乘客确认或拒绝.如果乘客拒绝该价格,平台将取消该订单.
2) 路线规划.路线规划阶段指的是平台为订单中的乘客指派司机并为该司机提供行驶路线的过程.在这一阶段中,平台调用路线规划模块,通过部署的路线规划算法对乘客提交的订单进行分配,即根据内部的优化目标指派某位司机服务该订单,并为该司机规划路线.
3) 完成订单.完成订单阶段指的是司机执行接送乘客任务以及乘客被送达终点后的处理过程.在司机执行接送任务的过程中,平台调用人身安全保障模块来保护乘客与司机的人身安全.在乘客被送达后,平台需要调用激励机制模块决定乘客需向平台支付相应的费用,并接受乘客对司机的服务评价,同时决定司机从中获取的报酬.
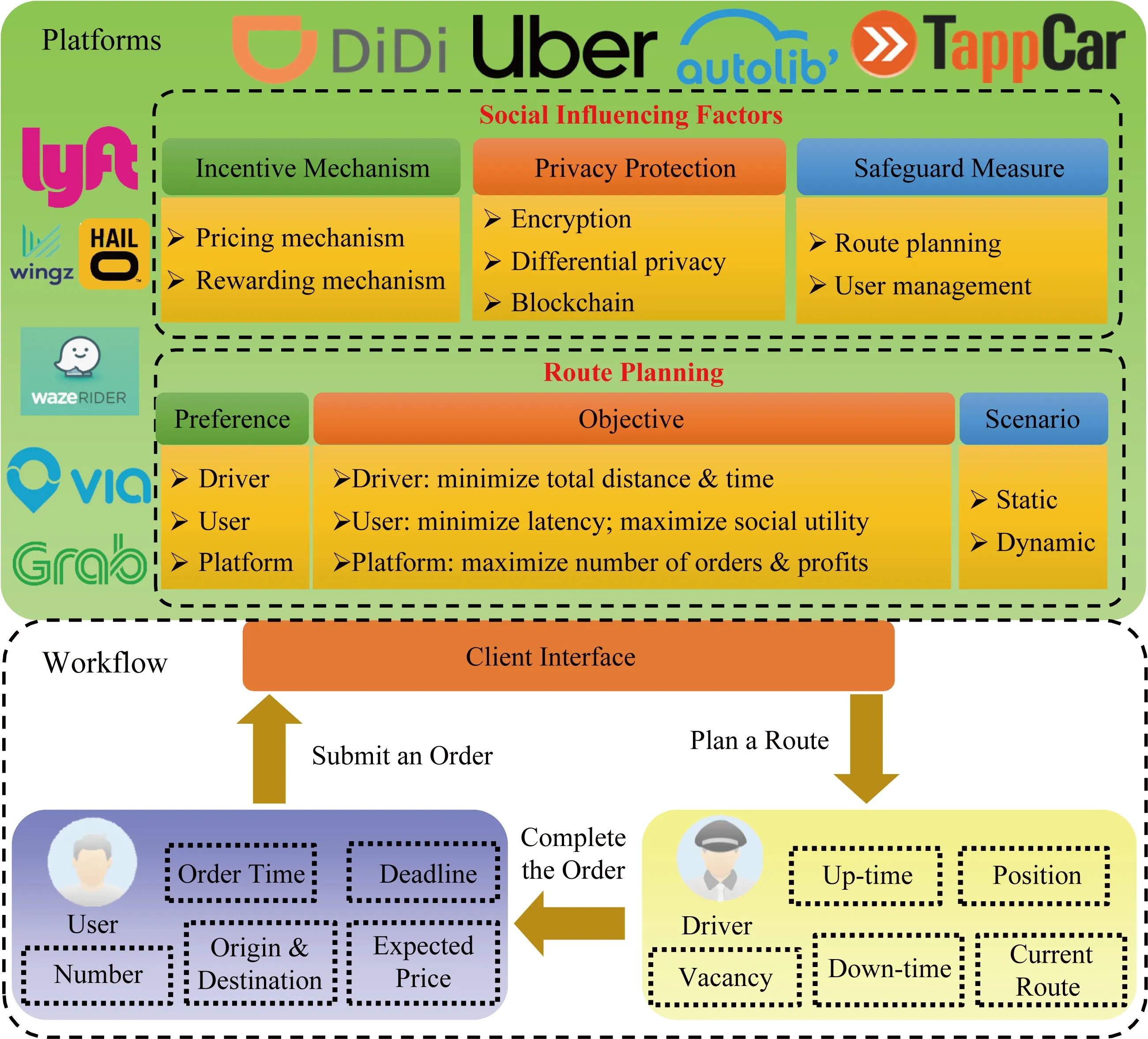
Fig. 1 The workflow of ridesharing platform图1 拼车平台的工作流程
2 路线规划
路线规划是大规模拼车平台工作流程中最为核心的问题.对平台而言,路线规划算法往往决定了司机的工作效率、乘客的出行体验和平台的盈利情况等.本节根据偏好角度的不同对现有路线规划的相关研究进行分类,分别从司机角度(2.1节)、乘客角度(2.2节)和平台角度(2.3节)对现有文献进行阐述和分析,最后对这些文献进行了总结(2.4节).
2.1 基于司机角度的路线规划
对司机而言,其通常希望以更短的距离服务指派的订单,或在更短的时间内完成被指派的订单.因此,从司机的角度进行路线规划,常用的优化目标包括最小化司机行驶总距离和最小化司机最大完工时间.
2.1.1 最小化司机行驶总距离的路线规划
最小化行驶距离是解决拼车中路线规划问题的文献中主要的优化目标.这一类问题的基本模型即1.2节所述的拨号叫车问题.该问题为单个司机和多个订单进行路线规划,从而在满足一定约束的条件下最小化司机的行驶距离.根据业务场景的不同,这部分研究又可分为2类,即针对静态场景的研究和针对动态场景的研究.在静态场景中,通常假设所有订单的信息初始即已知;而在动态场景中,订单信息仅在发布时才能由平台获知.由于信息的不确定性,动态场景中的路线规划问题通常难于它在静态场景下的对应问题.
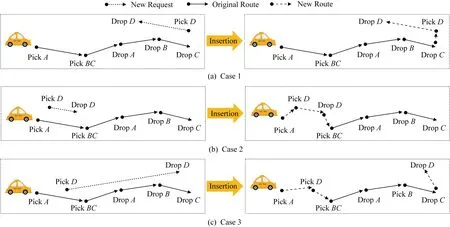
Fig. 2 An illustration of the insertion operation图2 插队操作的示意图
此后,Gupta等人[20-21]针对拼车中最小化行驶距离的路线规划问题,提出了基于k-森林问题的近似算法,该算法具有近似比保证.具体来说,k-森林问题旨在从n对起点和终点中选择k对构成1个连通子图,并使得该子图的连通花销最少.文献[20]所提出算法的基本思路是将k-森林问题中的k值设置成司机的容量大小,从而使用k-森林问题的近似算法每次从余下订单中选出不超过k个订单(即不超过容量限制).
近年来,更多的文献关注拼车平台中动态场景(也称为实时场景)下的路线规划问题. 其中,这些文献提出的算法主要可以分成2类:基于插队的算法和基于匹配的算法.
为了在动态场景下解决以最小化行驶距离为目标的路线规划问题,大多数文献[22-25]基于插队操作来设计算法.插队操作最早由Jaw等人[26]提出,其基本思想如图2所示.在执行1次插队操作之前,首先给定司机的当前行驶路线和1个新发布的订单,而插队操作旨在将这个新订单的起点和终点分别插入到原有路线中,从而获得新的路线并使得司机的行驶距离尽可能短.对于这对起点与终点插入位置,插队操作共有如图2所示的3种情况:1)新订单的起点和终点相邻地添加至当前路线的末尾(情况1);2)新订单的起点和终点相邻地插入至当前路线的开始位置或中间位置(情况2);3)新订单的起点和终点不相邻地插入到当前路线的中间位置(情况3).值得一提的是,插队这一操作不仅适用于动态场景,也经常被应用于静态场景中.
Ma等人[24-25]将插队操作应用到面向路网的路线规划问题中.他们实现了一个时间复杂度为O(n3)的插队算法,其基本思想是分别枚举新订单中起点和终点的插入位置并检查新路线是否满足约束条件,在所有满足约束条件的路线中选择距离增量最短的一条作为新路线.为了解决多个司机、多个订单的路线规划问题,他们提出了T-Share框架.该框架能够实时地处理每个订单,并依据截止时间等时空约束条件筛选可被分配的司机,从而通过插队操作计算每个筛选后的司机为了服务新订单所增加的行驶距离,最终指派行驶距离增加最少的司机来完成该订单.为了加快算法的运行时间,他们还采用了基于网格的空间索引以及双向搜索算法来筛选司机.实验证明:与不使用拼车算法的出行方式比较,他们提出的算法能够在多完成25%订单量的同时减少13%的行驶距离.
在T-Share框架的基础上,Huang等人[23]提出了一种基于字典树的数据结构,即活动树(kinetic tree).在活动树中,每条从根结点到叶子结点的路径都代表了对应司机在当前时刻下的一条可行路线,而司机总是按照总距离最短的路线行驶.每当一个新订单到来时,他们提出的算法通过在活动树上递归的方式计算新订单插队后增加的行驶距离,其中每次插队操作需要O(n2)的时间复杂度.最后,该算法将保留所有满足约束条件的可行路线并相应地更新整棵活动树.由于可行路线的数量在最坏情况下会达到指数级,他们还进一步提出了基于热点聚类的活动树(hotspot-based kinetic tree).考虑到其良好的实验结果,该数据结构被部分相关文献[27-28]所采纳和应用.
Santi等人在文献[29]中同样采用了插队算法来解决拼车的路线规划问题.首先,他们尝试将不同的订单聚合成组.其次,将所有的组按照距离排序.然后,尽可能多地将每个组内的订单插入到当前司机的路线中.特别地,他们采用一种基于批次(batch)的路线规划方法,即每隔一段时间对当前批次内积攒的订单独立进行路线规划.
在文献[23-25,29]中,插队操作存在着时间复杂度较高的缺陷.为了解决这一缺陷,Tong等人在文献[22]中首次提出了基于动态规划的插队算法,将时间复杂度从平方复杂度降低为线性复杂度,并进一步提出了基于线性时间插队操作的通用框架,大幅度减少了在路网中进行冗余的最短路径查询.通过在大规模路网上进行真实数据的实验测试,该文献证实了其所提出的算法pruneGreedyDP远远优于文献[23-24,29]所提出的算法.通常情况下,文献[22]提出的算法可以提升优化目标多达12.8倍,同时其运行时间还降低至4.83%.
除基于插队操作的算法外,基于匹配模型的算法也在相关文献中得到应用[30-31].在文献[30]中,作者假设每辆车的容量不超过2,并在这个前提下为每位司机规划路线.作者首先从3维匹配问题进行规约,证明了该特殊情况下的路线规划问题依然属于NP-难问题[32].文献[30]进一步提出了近似比为2.5的近似算法解决静态场景下的路线规划问题.该算法的基本思想是先枚举每2位乘客拼单的所有情况,再构建表示司机和枚举路线间关系的二分图,然后通过求解二分图最小权和匹配的匈牙利算法找到近似解[33].
与之不同地,文献[31]聚焦在动态场景下的路线规划算法,并采用了基于批次的分单方法.此外,该文献假设同一批次内的订单不会被分配到同一辆车中,从而构建能够表示司机与该批次订单关系的二分图.最终,Ta等人[31]通过执行二分图上的连接操作完成对每位司机的路线规划.
2.1.2 最小化司机最大完工时间的路线规划
尽管大多数从司机角度优化路线的文献旨在减少行驶总距离,仍有少部分文献[34-36]聚焦在最小化所有司机中的最大完工时间,即最小化所有司机完成最后一个订单的时间.
Ascheuer等人[35]主要解决动态场景下面向单个司机和多个订单的基于最小化司机的最大完工时间的路线规划问题.他们首先提出了2种解决框架:重新规划框架(REPLAN)和暂时遗忘框架(IGNORE).重新规划框架的核心思想是对于每个新到来的订单,都实时地与当前未完成的订单一起重新执行路线规划算法.相应地,暂时遗忘框架的核心思想是先由司机按照原有路线完成部分订单后,再对积攒的订单统一进行路线规划,最后由司机继续完成这些被暂时“遗忘”的订单.显然,后者执行的面向单个司机和多个订单的路线规划算法次数更少,因此其运行时间通常更短.同时,他们还证明了2个框架在对手模型(adversarial model)下的竞争比都是2.5ρ,这里ρ表示静态场景下解决面向单个司机和多个订单的最小化行驶距离的近似算法的近似比.最后,结合2种算法,他们提出了一种智能启动(SMARTSTAT)算法,该算法能够自适应地对积攒的订单执行面向单个司机和多个订单的路线规划算法,并将竞争比提高到2ρ.
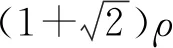
2.1.3 司机角度路线规划小结
表1总结了基于司机角度进行路线规划的主要算法研究.

Table 1 The Summary of Algorithms on Route Planning from Drivers’ Perspective表1 基于司机角度的路线规划算法总结
就算法的应用场景而言,可以发现当前研究趋势正从静态场景转变为更加通用的动态场景,且近期研究多针对大规模的拼车数据(订单量最高可达到百万级别),这也反映了人们日常出行中对拼车服务的需求和依赖[22].
就算法的运行效率而言,通过比较算法时间复杂度可以发现:文献[22]所提出的算法prune-GreedyDP具有最低的时间复杂度,并通过大规模的真实数据验证了算法的实际运行效率.此外,这些算法往往需要通过大量的插队操作来规划路线,因此,如何高效地将插队操作与时空索引结合,是未来进一步提升算法运行效率的潜在方法.
就算法的近似效果而言,通过比较算法近似比或竞争比可以发现,现有研究仅在单个司机的情况下具有近似效果的理论保证.当问题变得更加复杂时(例如多个司机的情况),暂无研究提出具有理论保证的近似算法.基于此,是否存在更通用问题场景下对数阶乃至常数阶近似比或竞争比的算法仍是一个开放问题.
2.2 基于乘客角度的路线规划
在对拼车请求进行路线规划时,乘客往往希望该路线尽量少绕路从而可以尽快到达终点.此外,最新研究表明乘客还希望能够与彼此间友好的乘客共享行程.因此,从乘客的角度进行路线规划,常用的优化目标通常包括最小化等待时间和最大化社会效用.
2.2.1 最小化乘客等待时间的路线规划
在大规模拼车问题中,乘客在向平台提出请求后,往往希望能够尽快到达其终点.从乘客角度进行路线规划,一个很自然的想法就是最小化乘客的等待时间.
Psaraftis[37]于1980年使用所有乘客中的最大等待时间衡量乘客的不满意程度,即以最小化所有乘客中的最大等待时间为目标来进行路线规划,进一步证明了在拼车问题中基于该目标的路线规划问题属于NP-难问题.因此,他们提出了一个指数时间复杂度的精确算法,可以解出小数据规模下(订单数量通常不超过10)的最优解解.为了解决更大规模订单下的路线规划问题,Jaw等人[26]采用了基于最小化乘客的最大等待时间的插队操作,即以最小化乘客的最大等待时间作为插队操作的优化目标.其基本思想是枚举每个订单来尝试插入到所有司机的已规划路线中,并最终把订单指派给使得最大等待时间增加最小的司机.尽管该算法的时间复杂度从指数时间降低到了多项式时间,但却依然只能快速地处理订单总数不超过3 000规模的数据.该算法低效的主要原因是其对插队操作的实现需要3次方的时间复杂度,为了降低这一操作带来的时间开销,Xu等人[38]提出了基于动态规划的插队算法.其核心思想是通过动态规划将查询最优插队位置的操作转化为查询特定区间最小值的操作,从而采用动态区间的查询索引(如线段树或树状数组等)将时间复杂度降低到线性时间复杂度.实验证明该方法可将插队操作加快最高达998.1倍.Krumke等人[39]研究了在动态场景下最小化乘客的最大等待时间的路线规划问题,并证明任何确定性或随机算法都不存在常数竞争比.
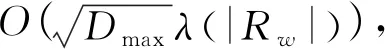

Fig. 3 An illustration of the RTV-Graph图3 RTV-图的数据结构示意图
2.2.2 最大化乘客社会效用的路线规划
社会效用(social utility)一直是出行平台中路线规划问题的常用目标之一[43-48].为了提高乘客在大规模拼车中的出行体验,现有文献也开始关注拼车服务中共享行程的乘客之间、司机与乘客之间的社交关系.例如,首先通过定义社会效用模型来表示乘客间是否适宜共享行程、是否具有相同偏好等社交关系,然后再根据社会效用模型进行路线规划.
Kameswaran等人[49]通过对Uber公司的司机及搭载的乘客进行调研,发现了社交关系在拼车平台中的重要性.具体地,文献[49]发现乘客们往往希望能够与性格相似的人共享行程,甚至希望在行驶过程中彼此可以通过交流打发时间.此外,还有一些乘客可以接受一些比较绕路的行驶路线,但前提条件是行驶途中可以经过一些如风景名胜等特定地点.文献[50-51]进一步探究了大规模拼车问题中以最大化社会效用作为优化目标的路线规划问题.其中,Cheng等人[50]在社会效用模型中既考虑了乘客间的社交网络关系,还考虑了乘客与司机间的社交网络关系.具体而言,乘客r和司机c之间的社会效用函数为
μ(r,c)=α×μv(r,c)+β×μr(r,c)+γ×μt(r,c),
其中,函数μv表示乘客r和司机c的社交因素指标,函数μr表示乘客r和司机c所搭载的其他乘客间的社交因素指标,函数μt表示乘客r对所规划路线的满意程度,而参数α,β,γ用来衡量三者之间的权重关系.文献[50]进一步提出了静态场景中的以最大化社会效用为优化目标的路线规划问题,并证明了该问题不存在任何具有常数近似比的算法.因此,文献[50]采用基于插队操作的启发式算法解决该问题,并在2个大规模真实数据集上进行了实验.Fu等人[51]提出基于社会效用的Top-k路线查询问题,即为每位乘客提供社会效用最大的k条候选路线,由乘客根据自己的偏好进一步选择.该文献提出2种不同的过滤候选司机的算法,即基于边的过滤算法和基于网格索引的过滤算法.
2.2.3 乘客角度路线规划小结
表2总结了基于乘客角度进行路线规划的主要算法研究.
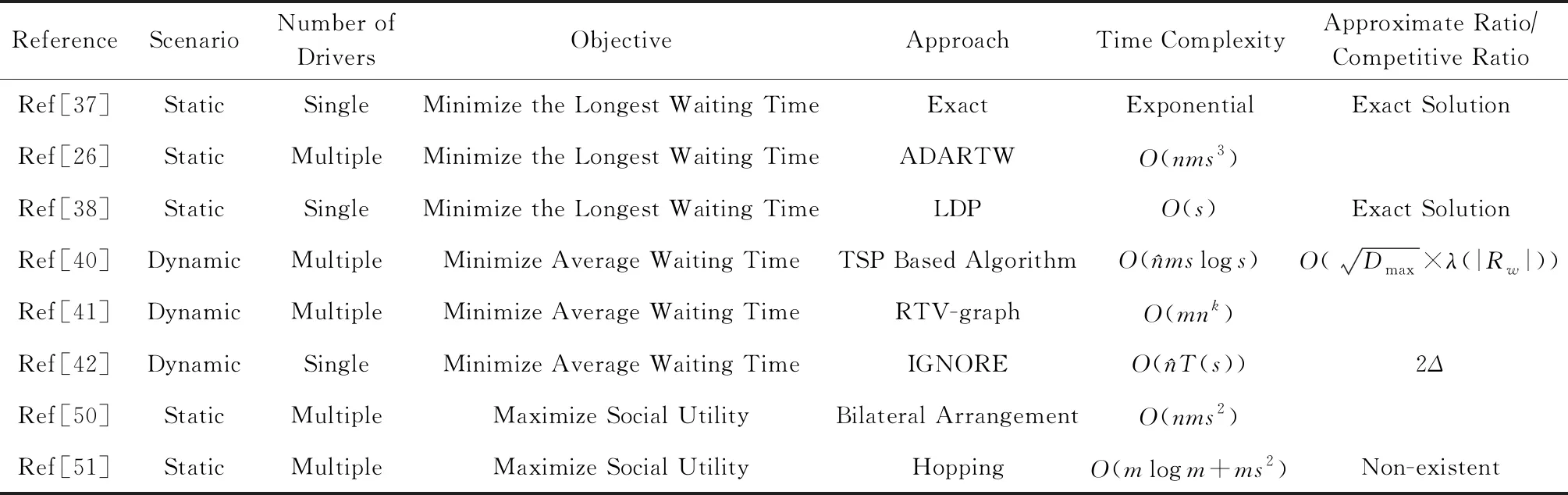
Table 2 The Summary of Algorithms on Route Planning from Passengers’ Perspective表2 基于乘客角度的路线规划算法总结
就算法的应用场景与优化目标而言,可以发现目前研究大多局限于静态场景,而对动态场景的探索略为欠缺.同时,传统研究多聚焦于最小化乘客等待时间等简单量化目标,而近2年的文献[50-51]侧重于优化拼车过程中的用户体验,如乘客和乘客间的社交关系以及乘客与司机间的社交关系等,由此可见人文关怀在拼车中愈发重要.如何有效度量并且高效计算社会效用成为了新的挑战.
就算法的运行效率与近似效果而言,虽然早期研究提出了一些精确算法,但其只针对小规模数据而无法适用于当前真实拼车平台的大规模订单需求.而目前适用于大规模场景的算法中,文献[40]提出的算法具有最高的运行效率,且是现有文献中唯一对多个司机的情况具有理论保证的算法.但该理论保证要求订单的时空分布满足严格的假设条件,而这些假设可能并不符合实际应用(如要求订单的位置信息满足均匀分布等).因此,如何在合理的假设前提下设计具有近似理论保证的高效算法仍具有很大挑战.
2.3 基于平台角度的路线规划
在进行路线规划时,拼车平台关注的焦点往往是订单完成数量以及平台的总盈利.因此,从平台的角度进行路线规划,常用的优化目标包括最大化平台的订单完成数和最大化平台的总收入.
2.3.1 最大化平台订单完成数的路线规划
拼车平台往往从自身盈利的角度出发规划合适的路线.由于受到时空约束的限制,实际平台中用户请求的拼车订单无法保证全部完成,从而存在平台拒单或者要求用户等待分配的情况.因此,一个自然的优化目标是最大化平台的订单完成总数量,即在满足约束条件的情况下为尽可能多的乘客提供服务.
Kleiner等人[52]首先提出了一个以最大化平台的订单完成数为优化目标的智能动态拼车系统DRS.该系统采用拍卖机制,即每个司机先对自己喜好的订单进行投标,最终由平台来决定每个订单该如何指派,并为指派的司机制定行驶路线.文献[52]证明了这一基于拍卖机制的拼车系统具有激励相容(incentive compatible)的性质.在进行路线规划时,该系统先计算每位司机接送若干位乘客的行驶距离矩阵,然后利用3次方时间的匈牙利算法求解分配方案,从而再确定每位司机接送乘客的先后顺序.Santos等人[53]额外考虑了乘客的花费因素,即他们希望找到一条最优路线,既可以最小化乘客花费,又能够最大化订单完成数量.在为司机进行路线规划时,该文献依然采用了基于插队操作的局部搜索算法.
Cici等人[54]在其工作中证明了最大化订单完成数量的问题实际等价于最小化所需司机数量的问题.Vazifeh等人[55]则进一步提出了一个基于交通网络的算法解决最小化用车数量这一等价问题.该问题旨在满足时空约束的条件下完成所有的订单,并最小化所需要的司机数量.大量基于真实数据的实验表明该算法仅使用70%的车辆即可完成全部的订单.作者还前瞻性地认为该算法也可以用于无人车的调度系统中.此外,现有文献还考虑了一些真实系统中的环境因素.例如文献[56]还考虑了在实际路网中具有不同类型的道路前提下如何设计路线规划算法.
2.3.2 最大化平台总收入的路线规划
从平台角度考虑,另外一个自然的优化目标是最大化平台的总收入.在实际系统和现有文献中,平台的总收入往往被定义为所有乘客支付的订单价格总和减去平台支付给所有司机的报酬.
Asghari等人[57]首先分析了在动态场景下,不存在具有常数竞争比的确定性算法能够近似地解决基于该目标的路线规划问题.随后,他们提出了一种基于分支定界的框架APART,递归地尝试为每个新来的订单找到当前最优的司机.实验结果证明,该算法获得的平台总收入显著优于基于活动树的算法[23]和基于最近邻搜索的算法[58].
文献[59-60]都采用了基于二分图匹配的算法,其基本思路与文献[29]的想法类似,即先尝试把可共享的若干订单(通常不超过容量限制)进行聚合(也被称作将订单打包),再一次性地把打包好的订单分派给一位司机.考虑到订单打包这一环节往往需要枚举遍历所有的可能组合,并进行大量的在线最短路径查询,该方法并不适用于高容量限制、大规模路网的场景.例如,文献[59]假设汽车的容量限制不得超过3.
文献[22]提出了一个统一的优化目标,该目标既可以等价地转化为最大化平台的订单完成数,也能够等价地转化为最大化平台的总收入.他们进一步分析了该问题的复杂性,证明该问题定义下任何确定性算法或随机算法均不存在常数竞争比.为了减少路网中的最短路径查询次数,该文献提出了一种使用欧氏距离执行预插队操作的剪枝策略.最后,基于百万级规模的真实数据的实验表明,该文献所提出的算法pruneGreedyDP远远优于基于二分图匹配来进行路线规划的经典算法[29].此外,因为剪枝策略而节约的最短路径查询次数多达579亿次.
2.3.3 平台角度路线规划小结
表3总结了基于平台角度进行路线规划的主要相关研究.
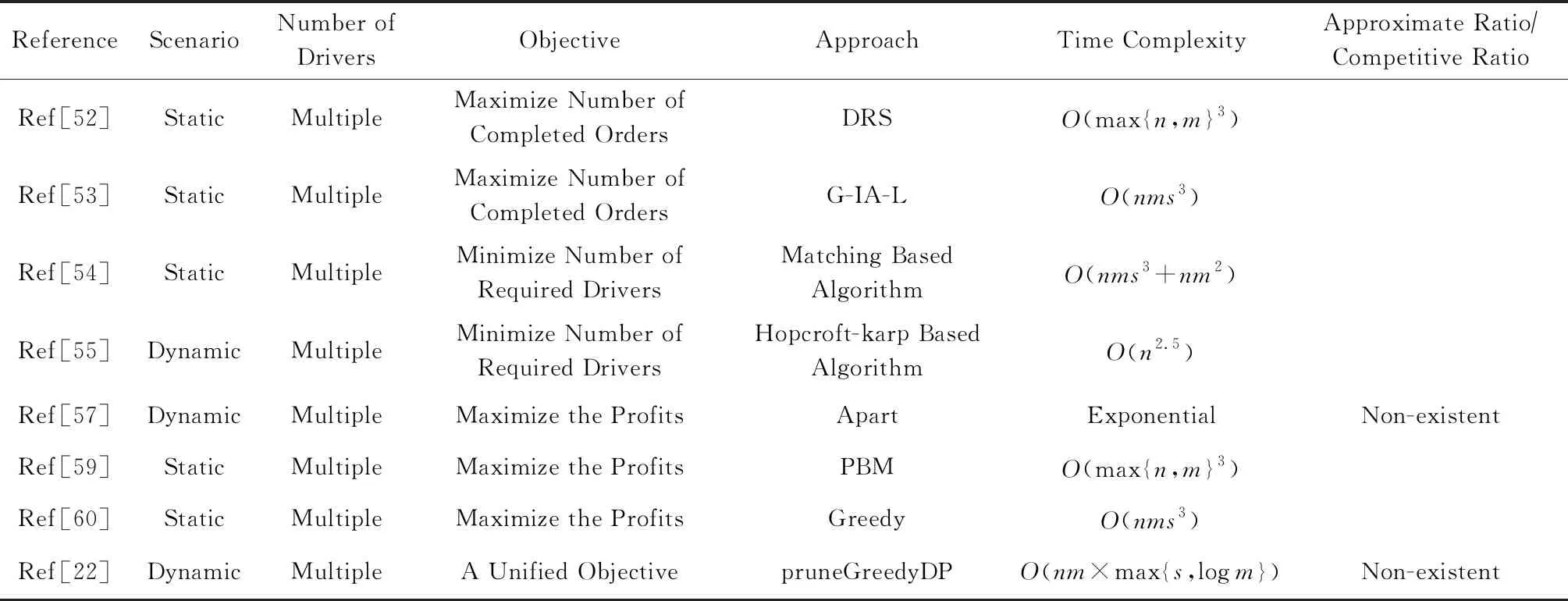
Table 3 The Summary of Algorithms on Route Planning from Platforms’ Perspective表3 基于平台角度的路线规划算法总结
就算法的运行效率与近似效果而言,文献[22]的时间复杂度在考虑各变量范围的情况下仍优于其他算法,是目前此类问题最高效的求解方案.该文献同时也证明了在动态场景中不存在具有常数竞争比的确定性算法或随机算法.因此,基于平台角度的路线规划的一个开放性问题是探索是否存在对数阶近似比或竞争比的算法.此外,除近似比或竞争比外,遗憾(regret)也常被作为算法理论保证的衡量标准之一[61].在基于最大化平台订单完成数的优化目标中,遗憾可以用来表示最优解的最大订单完成数与近似算法能够完成订单数的差值.在基于最大化平台总收入的优化目标中,遗憾则可以用来表示平台的最高总收入与近似算法能够获得的实际收入之间的差值.差值越小,则意味着算法的效用更好.但是,现有文献均以探究近似比或竞争比为主.因此,另外一个开放性问题是现有算法或新算法是否可以在遗憾这一理论保证指标上具有好的分析结果.
2.4 路线规划算法总结
表1、表2和表3分别从司机、乘客和平台角度对大规模拼车的路线规划算法进行了分析和对比.综合这3个表格可见,现有研究往往仅针对司机、乘客或平台的单一角度对路线进行规划.然而,作为一个典型的双边市场,拼车平台需要同时兼顾司机和乘客的用户体验.此外,只有少量工作提出了具有理论保证的近似算法,且往往仅针对1个司机、多个订单的场景.而对于多个司机和多个订单的离线场景或在线场景,几乎没有任何文章提出具有理论保证的算法.最后,现有研究的另一个假设是其仅针对欧氏空间或者静态路网设计路线规划算法,而所述方法通常难适用于反映实时交通情况的复杂路网环境,因而在实际应用场景中具有一定局限性.
此外,在真实平台中使用路线规划算法时,还需要考虑一些实际因素.例如乘客对起点和终点的选择与实际的GPS位置存在一定误差,因此平台需要依赖大量的上车地点和下车地点候选集减小该误差.而司机可能存在不熟悉行驶路线的情况,因此平台应该在保证优化目标的前提下优先对熟悉路线的司机进行指派和分单.
最后,现有研究还存在一些假设过强之处,例如:总假设乘客不会临时取消订单、司机从不拒绝平台所指派的订单等,然而实际拼车平台(如滴滴出行等)常有违背这些假设的情况发生[1].针对第1种情况,当乘客临时取消订单时,平台将该乘客取消订单的情况实时地通知给所指派司机,并从为司机规划的路线中删除该乘客的起点和终点,从而保证司机仍然能够顺利地接送后续乘客.此外,在订单高峰期,司机可能仅愿意接受具有更高利润的订单,而出现拒绝某些低利润拼车订单的行为,但现有算法往往不适用于该情况.因此,如何在路线规划问题中考虑挑单和拒单等行为也是未来的研究方向.
3 社会影响因素及相关解决方案
除了路线规划这一核心,大规模拼车平台的工作流程还涉及了诸多社会影响因素.其中,最主要的因素包括如何对司机和乘客的积极性进行调动,以及如何对他们的隐私和人身安全等进行保护.基于此,本节分别对激励机制(3.1节)、隐私保护(3.2节)和人身安全保障(3.3节)等社会影响因素进行阐述、分析和总结.
3.1 激励机制
大规模拼车问题中的激励机制指通过增加司机收入、降低乘客花费等手段吸引他们参与拼车,从而扩大拼车服务市场、提高拼车平台收益的各种方法.按照是否直接使用价格进行激励,可以将广泛研究和投入实际应用的激励机制分为基于定价的激励机制和基于奖励的激励机制2类.
3.1.1 基于定价的激励机制
大规模拼车问题中,乘客向平台支付费用以获取服务,司机通过接送乘客从平台获取报酬.基于定价的激励机制指通过向乘客收取合理的费用和向司机支付合理的报酬来激励乘客和司机参与的激励方式.根据价格是否实时调整,基于定价的激励机制可进一步分为2类:基于固定价格的激励机制和基于浮动价格的激励机制.
1) 基于固定价格的激励机制
基于固定价格的激励机制(俗称“一口价”)指乘客所需支付的费用和司机从每份订单获得的报酬均在订单行程开始前确定,不因拼车过程中新乘客的加入、路线的变更等导致额外时间花费的因素而实时调整.
文献[62]使用双边拍卖模型(double auction model)对基于固定价格的激励机制进行建模,以此设计分单算法来匹配司机和任务.该文献首先以司机和乘客的预期价格为基础,结合个人信用等因素,生成综合分数.其次,迭代地将乘客和司机的综合分数分别按照降序和升序排列,并对司机和乘客进行匹配.该文献提出的机制具有真实可信(truthfulness)的性质,即乘客和司机均愿意按照其真实的心里预期价格进行报价,且能够保证平台收支平衡.实验结果表明,在该文献所提出的定价方式下,成交订单数较双边VCG拍卖模型有所增加,而总成交额仅略低于最优定价模型下的总成交额.
文献[63]同时考虑现有订单和未来订单的弹性需求来制定长期的定价机制,并从长远角度考虑增加社会福利.该文献认为拼车定价问题若忽略实时变动的弹性打车需求,会产生福利预期过高和服务效率过低的问题.因此,作者将长期定价的思想应用到动态拼车问题中,将拼车的定价问题建模为排队理论中的多服务器排队模型,从而研究以社会福利作为优化目标的定价问题.实验表明,在使用相同路线规划算法的前提下,该文献所设计的定价机制可以获得更高的社会福利.
文献[64]研究如何通过制定价格的方式使平台收益最大化.具体来说,平台在时刻t位于区域i的收益可形式化地表示为
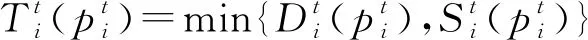
Wolfson等人[65]研究了拼车过程中针对不同乘客进行收费的公平性问题.在使用拼车服务时,不同乘客间拼车会产生不同的费用,乘客倾向于寻找使其花费最小的乘客分享行程.文献将其建模为一个图上的匹配问题并提出GRF(guaranteed-ridesharing-fairness)定价机制.具体而言,首先计算全局最优匹配和个体公平匹配2种方案,然后在实现全局最优匹配方案的同时按照个体公平匹配方案的定价机制收取费用,最后将全局最优匹配方案的剩余利润平分给各个乘客进行补贴.这种方式既保持了对社会福利的最大化,又能保证参与乘客的个体公平性.
2) 基于浮动价格的激励机制
基于浮动价格的激励机制指乘客所需支付的费用和司机从每份订单获得的报酬均基于具体的行驶路线或时间花费等因素并按照某种规则实时调整.
Ma等人[24]基于动态场景下针对多个司机的路线规划问题,提出了基于浮动价格的激励机制.在该定价机制中,为了激励更多司机和乘客参与,司机收取的单位距离费用以一定比例高于非拼车模式(即正常打车模式)的价格.例如若正常打车模式中每公里费用为p元,则司机在拼车模式下每公里将可以获得p乘以(1+α)倍的报酬,这里α表示额外获得报酬的系数.相应地,若司机正在服务d名乘客,则每个乘客在该公里的费用为(1+α)pd元.然而,该基于浮动价格的激励机制有可能导致乘客的实际支出高于正常打车模式的支出,降低乘客对拼车的兴趣.
Ma等人在文献[25]中扩展了文献[24]中的思想.该文献首先提出为激励司机和乘客参与拼车过程,基于定价的激励机制应具备的3个性质:1)乘客使用拼车服务所付费用应小于其使用正常打车模式所付费用;2)在拼车过程中受到绕路影响的乘客,其所需支付费用应获得一定折扣;3)付给司机的报酬需要涵盖司机为了接单行驶的总距离.为满足这3条性质,文献[25]提出了以下基于浮动价格的激励机制.对乘客而言,其所需支付的费用由2部分组成:一部分为正常打车模式下的费用减去平台预设的一个常数f,这里f相当于乘客使用拼车服务得到的优惠;另一部分是司机为了接送新订单绕路而导致的额外费用.对司机而言,其所获得的实际报酬为其服务的所有乘客支付的费用之和.文献[25]同时证明了该基于浮动价格的激励机制符合其所提出的3点性质.
文献[57,66-67]将拍卖理论应用到基于浮动价格的激励机制设计.Asghari等人[57]研究了以最大化平台收入为优化目标的定价问题.具体来说,每个司机具有一个私有的费用衡量函数,表示其行进一段距离所需要的花费.而每个乘客具有一个费用折扣函数,表示因新订单插队导致的绕路距离与支付费用折扣的映射关系.这一折扣函数保证乘客支付的费用不会高于其使用正常打车模式的费用,因而能够激励乘客使用拼车应用.平台最终的收益等于乘客支付的总费用与平台支付给司机的总报酬的差值.为解决该问题,文献[57]提出了基于拍卖思想的定价模型.即乘客在平台发布订单后,附近司机分别估计其接受该订单所需的报酬并作为报价.平台根据司机的报价将订单分配给报价最低的司机完成.值得注意的是,文献[57]的这种定价方式能够保证乘客所付费用低于正常打车模式的费用,因而能够激励乘客参与拼车.
针对文献[57]中司机在自主计算行驶费用过程中可能汇报虚假价格的问题,Asghari等人进一步在文献[66]中指出,对于司机来说,拼车中基于定价的激励机制应满足2个性质:1)真实可信,即司机虚报价格所得到的收益应不大于其如实报价所得到的收益,这能够保证司机的报价都是真实的;2)个体理性(individual rationality),即司机所获得的收益应不少于其行驶开销,该条性质保证司机愿意参与到拼车中.基于文献[57]提出的问题定义和定价框架,文献[66]引入拍卖理论中的第二价格密封拍卖,使得预估报酬最低的司机获得订单,但将次低的预估报酬付给司机.该文献证明上述基于定价的激励机制满足真实可信和个体理性的性质.在真实数据集上的实验进一步表明,文献[66]提出的定价机制具有与文献[57]几乎相同的平台收益.
文献[67]在最大化平台收益的目标下,从乘客角度研究如何设计具有真实可信性质的基于浮动价格的机制.具体来说,文献[67]提出了基于贪心和基于订单排序的订单分配算法,并通过寻找临界费用(critical payment)的方式确定向乘客收取的每公里价格,并证明了其定价机制对于乘客来说具有真实可信的性质,即能够使得乘客汇报真实的对每公里价格的预期.实验表明,该文献提出的算法运行效率较好,而基于订单排序的算法能够获得更高的平台收益.
文献[68]研究以社会福利最大化为优化目标的基于浮动价格的激励机制设计问题,其具体优化目标等价于最小化拼车总花费(所有司机报酬之和)与所有订单最短距离之和的比值.平台首先估计乘客所提交订单的费用上界,并对接受该估计的乘客订单进行分配.对于被分配的订单,其单位距离的价格等于司机已支付报酬与已分配订单最短距离之和的比值.对应地,乘客所需付的费用为单位价格与其行进距离的乘积.该文献进一步证明了其所提出的定价模型具有真实可信的特点,实验表明其提出的定价模型较其他模型具有更高的社会福利.
3.1.2 基于奖励的激励机制
基于奖励的激励机制指通过积分、补贴、红包等方式对司机或乘客进行激励.根据奖励对象的不同,基于奖励的激励机制可分为面向司机的奖励方法和面向乘客的奖励方法.尽管现有文献对基于奖励的激励机制研究较少,但该种制度已被广泛应用于滴滴出行、Uber等主流拼车平台[1-2].
1) 面向司机的奖励方法
面向司机的奖励方法指平台使用奖励的方式激励司机参与并提供更好的服务,其主要包括司机评分和组队竞赛2种方式.
司机评分指拼车平台根据多种因素对司机进行综合评分,并根据评分决定是否优先为司机分配订单.司机评分机制被许多拼车平台采用,例如滴滴出行公司的“服务分”就是一种司机评分机制:乘客在订单完成后对司机的服务进行打分,而司机的“服务分”则在路线规划阶段提供给乘客[1-5].由于评分的高低会影响到司机是否被优先分配订单,这种机制能够有效激励司机提供良好的服务.
游戏化的组队竞赛是一种新颖的面向司机的奖励方法.例如在滴滴出行的组队竞赛中,司机以小组(6人左右)为单位参与到平台设置的竞赛活动中,平台考察小组的活跃时长、接单次数等指标,并对排名靠前的小组进行奖励[1].这些奖励既包括物质奖励,也包括诸如服务分等其他奖励.组队竞赛一方面能够以竞争的方式调动司机的积极性,从而使他们更有动力参与到拼车服务中;另一方面,小组内部各成员之间可以方便地进行交流沟通,从而能在一定程度上缓解司机的工作压力并使他们产生对小组以及平台的归属感.滴滴平台于2018年多次推出组队竞赛的活动,已经覆盖全国超过100个城市,结果显示司机的工作时长、接单数量都有所增加.
2) 面向乘客的奖励方法
面向乘客的奖励方法指平台给予乘客权益上的保障和价格上的优惠,从而激励他们使用拼车服务,其中包括积分政策、会员制度和红包优惠等激励方法.
积分政策指平台根据乘客打车的花费按照一定比例返还积分.当乘客的积分累计到一定数额时,可以通过平台的积分商城兑换商品或优惠券等.积分制度可以在一定程度上吸引乘客使用拼车服务,也能够帮助平台在同行竞争中可以获得一定优势.
会员制度指平台根据乘客使用拼车服务的次数设置乘客的会员等级,并向不同等级的会员提供不同程度的权益.例如,高等级的滴滴出行会员可以享受优先派车与免费升级为优享车等权益[1].会员制度能够激励乘客对同一平台的长期使用,从而防止乘客向其他同类平台的流失.
红包优惠指拼车平台不定期地给乘客发放打折券或红包,从而使乘客以低价享受到拼车服务.以滴滴出行为例,该平台周期性地向乘客发放打折券,以此激励乘客使用拼车应用[1].对于乘客而言,价格上的优惠能够直接激励他们使用拼车应用.此外,在每次订单结算后,平台也会向乘客随机发放红包,当红包累计到一定金额后可以一次性抵扣车费.
上述面向乘客的激励方法已经在实际平台中得到了广泛应用,但仍旧缺乏进一步的理论研究.
3.1.3 激励机制小结
表4列举了本部分涉及的各类激励机制.可以看出,大部分研究集中在基于定价的激励机制.其中,基于固定价格的激励机制具有2个优点:1)乘客在行程开始前获知价格并决定是否接受,不必承担行驶路线变化等导致的额外花销,减少了乘客利益纠纷的可能性;2)司机报酬不受行车路线影响,激励司机以最短行程和最快速度完成订单,能一定程度提高司机完成订单的效率.反之,基于浮动价格的激励机制的2个特点则使其更适合动态的拼车环境:1)乘客所需支付的费用和司机从每份订单获得的报酬均根据行驶路线或时间花费等情况实时调整,能够避免路线调整或突发意外等因素导致的收费不合理情况;2)该类机制能够保证司机所获得的报酬不低于实际花销,从而激励司机参与拼车.尽管现有文献分别基于不同的优化目标提出了不同的固定价格或浮动价格的定价机制,但现有文献往往仅针对这些定价方式的短期收益进行了实验比较.而在实际平台中,机制的稳定性也常常是一项重要的评估指标,系统地分析和评估现有定价机制是否可以达到稳定的长期收益可能成为未来潜在的研究方向.

Table 4 The Summary of Algorithms on the Incentive Mechanisms in Large-scale Ridesharing表4 面向大规模拼车的激励机制算法总结
此外,分别从司机和乘客角度介绍了实际应用中基于奖励的激励机制.这些机制对于激励司机参与拼车服务和激励乘客使用拼车服务具有良好的效果.然而,学术界对这些机制的量化研究还有所欠缺,这也成为未来潜在的研究方向之一.
3.2 隐私保护
在大规模拼车应用中,用户的隐私信息一方面包括乘客订单的起终点位置、司机的行驶轨迹等时空敏感信息,另一方面也包括乘客的住址和联系方式等个人信息.拼车平台需要在保护这些隐私的基础上进行路线规划等操作.因此,从隐私保护方法的角度对基于加密技术、差分隐私和区块链的隐私保护技术的研究成果进行阐述.
3.2.1 基于加密技术的隐私保护方法
基于加密技术的隐私保护方法通过加密技术对用户的隐私信息进行加密,而平台则使用加密后的时空信息进行路线的规划.现有研究主要基于同态加密技术(homomorphic encryption, HE).同态加密具有高可塑性(易于修改和扩展特性)、无需解密即可进行加乘运算等优势.
文献[69]提出了ORide(oblivious ride)机制以保护拼车服务中乘客与司机的位置信息,并在订单的分配过程中考虑最小化司机行驶总距离.该机制基于部分同态加密技术(somewhat homomorphic encryption, SHE),且不依赖可信的第三方服务器(trusted third server).具体流程为:司机和乘客的位置坐标经过加密后上传到拼车平台.之后,拼车平台通过加密后的数据进行计算并将候选司机发送给乘客的客户端.然后,由乘客选择合适的司机进行订单的分配并将结果返回给拼车平台.最后,乘客与司机通过私密频道交换各自的真实时空信息来保证隐私安全.文献[69]将基于同态加密技术的密文作为操作载体进行司机的筛选,通过对密文打包的方式降低计算开销.实验结果进一步显示,隐私保护机制在各种参数下均能取得较好的匹配结果.
与文献[69]类似,文献[70]中提出的SRide动态拼车系统也采用部分同态加密技术保护乘客和司机的位置信息.在不使用可信第三方服务器的前提下,文献[70]将加密后用户的时空信息映射到与时间相对应的时间戳和与位置相对应的空间网格内,并通过映射后的时空信息过滤候选司机,减少待匹配司机的数量,减少对加密信息的操作所带来的计算开销.最后,该系统在路线规划阶段,计算乘客与司机的预期接车地点的相似性,并以最大化相似性为指标完成订单分配.实验表明,SRide完成匹配任务的时间分别为5 s和9 s,运行时间相比于文献[69]大大减少.
文献[71]采用替换加密和换位加密等经典加密方法完成保护乘客位置信息前提下对拼车订单的分配,其基本思想是在订单分配过程中考虑密文间的相似度.具体地,拼车平台将乘客和司机加密后的信息转换为词向量,通过向量之间的相同位数来衡量信息的相似程度,通过依次比较乘客与司机之间的时间向量相似性和空间向量相似性来完成订单的分配.最后,文献[71]分别在真实数据与合成数据上进行了实验验证,结果表明如果允许司机进行跨区域接单,订单完成数量将大幅度增加.
3.2.2 基于差分隐私的隐私保护方法
除基于加密技术的隐私保护方法外,文献[72-73]与实际平台(如Uber等)采用基于差分隐私(differential privacy)的隐私保护方法[58,74-75].基本思想是通过对原有数据添加噪声保证司机与乘客的时空敏感信息不被泄露,然后基于添加噪声后的数据进行路线规划的计算.
Tong等人[72]采用了差分隐私技术保护乘客的位置信息,同时最小化司机的行驶距离.具体地,平台根据位置信息将司机分为不同集合,然后通过分析对偶变量(dual variable)对乘客与司机集合进行匹配.然后,在配对的司机集合与乘客集合内部进行匹配得到最终的匹配结果.Tong等人[72]同时引入一种联合差分隐私优化过程(jointly differential privacy optimization process),在进行集合匹配过程中用以保护乘客与司机的个人隐私.实验结果显示,Tong等人[72]将提出的JDP-Ride算法与不涉及隐私保护的基线算法进行比较,实验结果表明提出的JDP-Ride算法损失更小、实验结果更稳定.
此外,Andrés等人[76]提出了专门针对空间位置信息的差分隐私方法:地理信息不可辨别性理论(geo-indistinguishability theorem, Geo-I),以专门保护个人位置信息.具体来说,给定原始点集合X和噪声点集合Z,该理论要求对于任意的2个原始点x,x′∈X和噪声点z∈Z,所提出的隐私保护方法K需满足:
K(x)(z)≤eε×d(x,x′)K(x′)(z),
其中,K(x)(z)为原始点x映射为噪声点z的概率.该理论已被广泛应用于保护时空敏感的位置信息[77-78].文献[73]研究满足地理信息不可辨别性约束下最小化乘客平均等待时间的问题.首先提出了一种基线算法,对乘客的位置信息加入拉普拉斯噪声使其满足ε-差分隐私,然后在此基础上使用匈牙利算法对乘客与司机进行一次分配.针对该基线算法对车辆利用率低的问题,提出对未满座的车辆迭代地执行多轮匹配,将仍有空座位的车辆与未分派的新订单进行匹配,从而使得可以完成订单的车辆增加、乘客的等待时间减少.
3.2.3 基于区块链的隐私保护机制
区块链技术起源于比特币,本质上是一种去中心化(不依赖额外的第三方管理机构)的、开放性的(除交易各方私有信息被加密外,区块链数据对所有人开放)和匿名的(信息传递可以匿名进行)分布式数据库与计算范式,近年来受到学术界和工业界的广泛关注[79-82].文献[80]使用区块链中的私有链(private blockchain)达到隐私保护的目的.采用基于区块链的车雾计算技术(vehicular fog computing),并提出了一个高效的隐私保护拼车系统FICA,可同时保护乘客与司机的位置信息和轨迹信息.车雾计算使用一种叫做RSU(road side unit)的分布式计算单元处理用户的数据.在订单完成后,用户需要将交易记录上传平台用以后续审核,而这些记录可被用来还原乘客与司机的个人信息从而导致隐私泄露.为了方便管理的同时保护隐私安全,FICA使用RSU建立交易记录的私有链,在该私有链中仅支持拥有相应权限的用户执行写操作,用以保证数据的可审核性与私密性.文献[80]的实验结果显示在乘客和司机数量为1 000时FICA的匹配时间不超过14 s,且优于文献[69]提出的ORide系统.
3.2.4 隐私保护小结
表5总结了大规模拼车应用中隐私保护的相关文献.由表5中可以看出,大部分研究工作着力于在静态场景、保护隐私的前提下,指派合适的司机并规划合理的路线;少部分工作考虑了更具普适性的动态场景.
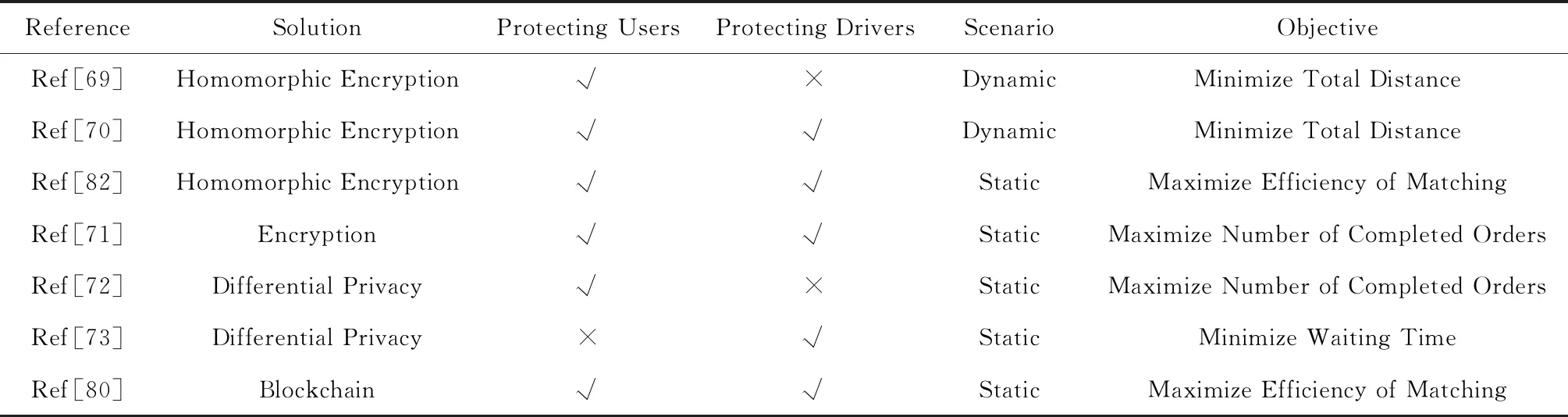
Table 5 The Summary of Algorithms on the Privacy Protection in Large-Scale Ridesharing表5 面向大规模拼车的隐私保护算法总结
3.3 人身安全保障
近年来,拼车平台涉及人身安全的恶性事件频发,引起了社会的广泛关注.如何在大规模拼车应用中保护乘客与司机的人身安全也成为一个不可避免的问题.现有研究通常从路线规划、用户管理等角度来考虑这一问题.
3.3.1 基于路线规划的人身安全保障
基于路线规划的人身安全保障旨在为司机和乘客选择安全的拼车对象和拼车路线.
文献[83]通过选择安全的拼车对象来保障乘客的人身安全.现有研究表明:出于安全考虑,人们更愿意和有直接或间接朋友关系的人一起拼车[84].据此,Wang等人[83]提出了一个考虑社交网络的拼车匹配算法.然而,将拼车服务仅限制在好友之间可能导致拼车匹配成功概率的降低和绕路开销的增加.为了解决这一问题,Wang等人[83]对比了基于3种不同社交关系限制条件的算法效果,即仅可与有直接社交关系的人(例如朋友关系)一起拼车、可与有直接社交关系或间接社交关系(例如朋友的朋友)的人一起拼车和可与任意乘客一起拼车.实验结果表明,具有特定空间分布的社交网络下,限制拼车仅发生在朋友之间所带来的额外绕路开销并不显著,且将存在良好社交关系的乘客优先匹配可以大幅提高朋友拼车率.
文献[85]通过选择安全的拼车路线来保障双方的人身安全,其依据是拼车过程中恶性事件往往发生在存在安全隐患的路段,或由司机擅自更改行车路线导致.文献[85]将乘客的上车、下车的地点固定为某一特定集合,并通过在这些地点加装监控来保障乘客和司机的安全.这种固定站点接送的方式同时还能够大幅度缓解交通拥堵.文章表明其所提出的方法能够平均减少31.5%的行驶距离.
3.3.2 基于用户管理的人身安全保障
基于用户管理的人身安全保障旨在通过建立合理的用户管理机制保障人身安全.
声誉管理机制是一种应用广泛的用户管理机制.文献[86]认为,乘客和司机的声誉对拼车平台而言至少有2方面的积极作用:1)良好的声誉可以帮助建立司机与乘客间的信任感;2)声誉可以促使乘客和司机为他们的行为负责,而恶意用户会因为较低的声誉值被辨别出来,并且受到惩罚.文献[87]提出一个分布式的声誉管理协议,根据与某一个用户(乘客或司机)接触过的其他用户的评价来为该用户计算一个全局的声誉值,并且确保这个协议能够让理性的用户们主动遵守从而做到互利共赢.当一个用户决定是否要与另一个用户拼车的时候,可以同时考虑根据他自身以往的接触经历计算出对方的局部声誉值和综合所有用户的评价计算出全局声誉值,取二者中的较低者作为参考.这一规则能够避免参与者有选择地对待某些用户.如果对方的声誉值高于该用户可接受的最低声誉值,则该用户可以信任对方并同意拼车.
此外,这一声誉管理系统还可以如3.1节所述作为激励机制发挥作用,即通过对声誉的管理促进用户遵守规章制度、减少违规操作.实验表明,良好的声誉能够让用户更容易地获得更好的拼车体验.具体来说,在声誉管理系统的激励下,用户更容易找到拼车对象,或能够以更短的行走距离前往上车地点.
工业界还使用一些其他的用户管理机制保障司机与乘客的人身安全.例如,滴滴出行要求平台的司机必须经过三证(身份证、驾驶证和车辆行驶证)验真的审核;通过对司机进行背景审查来构建司机画像从而降低暴力犯罪、酒后驾驶等违法行为的可能性(如图4所示);利用人脸识别技术核实实际驾驶员身份,严防冒用他人身份注册、私换驾驶员接单等行为;设置紧急联系人以便在危急时刻及时求助等[1-2,88].上述措施都是从加强对司机管理的角度保障乘客的人身安全.此外针对司机的人身安全保障,滴滴出行能够对司机的危险驾驶行为进行检测和实时预警,同时对于司机的异常停留等不当行为进行人工干预与检测,从而抑制危险状况的升级,以达到保障司机的人身安全的目的[1,3].
3.3.3 人身安全保障小结
表6总结了大规模拼车应用中人身安全保障的相关文献.可以看出,工业界已经采取了诸如用户管理等保障人身安全的措施并起到了良好的效果,但对相关机制的量化分析和理论研究还较为缺乏.
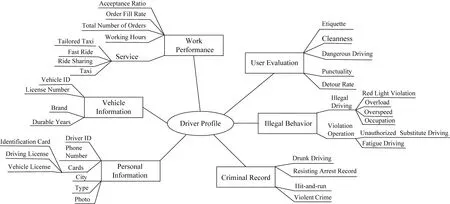
Fig. 4 An illustration of driver’s profile图4 司机画像举例

ReferenceSolutionProtecting UsersProtecting DriversScenarioObjectiveRef[83]Restrictions on Users√√StaticMinimize Total DistanceRef[85]Fixed Pick-up and Drop-off Locations√×DynamicMaximize the Coverage of DriversRef[87]Reputation Management√√DynamicMaximize Number of Completed Orders
4 未来研究方向
目前大规模拼车作为一个研究热点,仍有很多问题值得学者们深入研究.本节简述其中4类潜在的研究方向,供研究者们参考.
1) 有理论保证的路线规划算法
现存研究通常采用启发式算法解决多位司机、多个订单的路线规划问题,但尚缺乏针对该问题全局性能近似优化的理论分析.此外,现有研究仅从司机、乘客和平台的单方面考虑如何进行路线规划,这导致了所规划的路线难以同时对三者达到性能的优化.因此,现存的主要挑战是如何设计具有近似理论保障的路线规划算法,能够计算一条折中路线从而实现多目标优化.此外,现有研究的路线规划算法往往仅针对于欧氏空间或者静态路网,而不能解决复杂路网环境下所存在如堵车等实际因素.因此,如何将具有理论保障的路线规划算法扩展到复杂路网环境也具有一定挑战.
2) 混合普通打车的定价机制
尽管现有的拼车激励机制研究对多种定价方式进行了探索,但是这些研究假设乘客的出行方式仅拼车一种,而忽视了实际场景:在实际打车平台中,拼车模式往往与普通打车模式同时存在,即乘客可同时选择2类出行方式.因此同时考虑拼车与普通打车供需情况的定价策略显得更为合理.当供大于求时,平台能够仅通过普通打车来满足乘客的出行需求,此时若仍通过折扣的方式激励用户参与拼车,反而削弱了平台的收入.当供小于求时,平台由于车辆短缺难以通过普通打车来满足乘客的出行需求,此时适当增加对拼车模式的激励可以满足更多需求从而增加平台收入.因此,一个潜在的研究方向是混合拼车与普通打车供的定价机制设计.
3) 动态场景下的健全保障措施
拼车过程中的隐私保护及安全保障是近年来社会普遍关注的热点问题,然而相关文献在这方面研究不足.一方面,现存研究往往针对静态场景下如何保障用户的隐私,而忽略了实际应用中更为普遍的动态场景(即在线情况).因此,一个核心问题是在动态场景下,如何设计有效的算法保护用户的隐私、可行的机制保证用户的安全.特别地,现有关于拼车过程中人身安全问题的研究多为调研、案例研究性质的工作,缺乏在实际应用中从技术层面提出具体的措施来解决该类问题.由于隐私与安全问题与用户的切身利益息息相关,因此具有较大的研究意义.
4) 基于交互仿真的拼车模拟环境
为了验证拼车应用的路线规划、激励机制与隐私保护等算法问题,一个高性能的模拟环境必不可少.尽管现有研究已经提出了一些拼车的模拟器,但是它们的核心功能往往是提供司机和乘客的时空信息、分析统计算法性能等,而不具备与仿真算法的交互式验证[89-92].例如,为了验证激励机制的定价策略是否合理,模拟环境应该能够模拟乘客的心理预期和决策行为,即用户是否接受给定的价格.而现有模拟器往往不具备上述类似的功能.因此,为了更好地开展大规模拼车算法的相关研究,一个潜在的问题是如何设计一个基于交互式仿真验证的模拟环境.
5 结束语
本文介绍了共享出行中一类重要的应用——拼车,并针对大规模拼车算法的研究进展进行综述.文章首先介绍了拼车问题的基本概念和工作流程,随后对大规模拼车算法的核心问题——路线规划进行系统地讨论与分析,进一步对大规模拼车应用驱动的社会影响因素进行分类阐述.总的来说,大规模拼车问题在具有理论保证的路线规划算法、混合定价机制、动态场景保障措施和仿真拼车模拟环境等方向还具有潜在的研究价值.作为共享出行的一个重要应用形式,大规模拼车问题也为学术界提供了新颖的问题背景和研究动机,正在受到广泛关注,仍是大数据应用领域当前的研究热点之一.希望本文能够为大规模拼车算法研究领域的从业者们提供参考与帮助.
