固结体系斜拉桥一阶纵漂周期及桥塔地震剪力估算公式

何友娣， 王 巍， 沈文爱

(1. 中铁大桥勘测设计院集团有限公司， 湖北 武汉 430056； 2. 广州市市政工程设计研究总院有限公司， 广东 广州 510040； 3. 华中科技大学 土木工程与力学学院， 湖北 武汉 430074)

塔梁固结体系斜拉桥的结构刚度较大，因此，在高烈度区其地震响应也较大。此时，抗震安全性问题是桥型方案能否成立的决定性因素，故抗震设计是塔梁固结体系斜拉桥设计的首要环节[1, 2]。桥塔是斜拉桥最重要的受力构件，且自身属于高耸结构，因此是全桥抗震的重中之重。若能快速估算桥塔的地震响应，对工程设计的实用价值是不言而喻的。

在斜拉桥桥塔地震响应研究方面，徐艳[3]设计制作了某双塔斜拉桥比例模型，并通过振动台实验研究了不同方案的H形混凝土桥塔在横桥向地震作用下的破坏模式。夏修身[4]基于OpenSees平台建立斜拉桥模型，探讨了桥塔的非线性抗震性能。陈琼[5]利用有限元软件对大跨度斜拉桥桥塔结构进行抗震需求分析。叶爱君[6]建立苏通大桥有限元模型，将模型试验和数值模拟相结合，得到了地震下桥塔的屈服顺序和破坏位置。孙利民[7]进行了斜拉桥比例模型的横向振动台试验，揭示了A型混凝土桥塔的横向破坏模式具有明显的双塑性铰模式。可以发现，现有文献大多集中于不同桥塔形式、特点及其抗震性能的研究[8～12]，尚未将斜拉桥桥塔的地震响应与“塔梁质量比”和“塔梁线刚度比”关联起来，它们之间的数学关系尚未建立，造成实际应用过程中两个参数的选定具有很大的盲目性，工程设计极为不便。

若采用有限元仿真试算方法来解决这一问题，计算者首先需要对“塔梁质量比”和“塔梁线刚度比”给定不同的参数，然后建立有限元模型进行数据计算，最后通过数据拟合分析得到近似规律。整个过程需要设计人员不断地与有限元软件进行数据交互，计算异常繁琐且容易出现错误。这种依靠经验的试算方法有着巨大的工作量，计算处理耗时长，导致工程师无法承受，故该法不具备工程实用价值。本文基于力学原理，推导出一种能够计算塔梁固结体系斜拉桥桥塔地震内力的简化公式。

而关于斜拉桥一阶纵向振动周期的研究，袁万城等[13]在简化漂浮体系斜拉桥计算模型的基础上，推导了其纵飘频率简化计算方法。陈恒大等[14]利用Rayleigh法提出了考虑主塔刚度影响的三塔斜拉桥振动基频实用公式。张文学[15]采用柔度法推导了固定铰接体系斜拉桥纵向一阶频率的简化公式。但是，固结体系斜拉桥纵向振动基频简化计算方法的相关文献较少，《公路斜拉桥抗震细则》里也只给出了斜拉桥结构的竖向振动频率简化公式。结构的纵向自振频率是桥塔纵向地震响应的计算基础，因此本文推导了固结体系斜拉桥的一阶纵向振动频率及桥塔剪力的简化公式。

1 简化公式的理论推导

1.1 斜拉桥模型的简化

斜拉桥原始力学模型见图1所示，主要包括主塔、主梁和斜拉索，其中主塔和主梁之间的连接是固结体系，边跨主梁端部为活动支座，桥塔底部为固定支座。

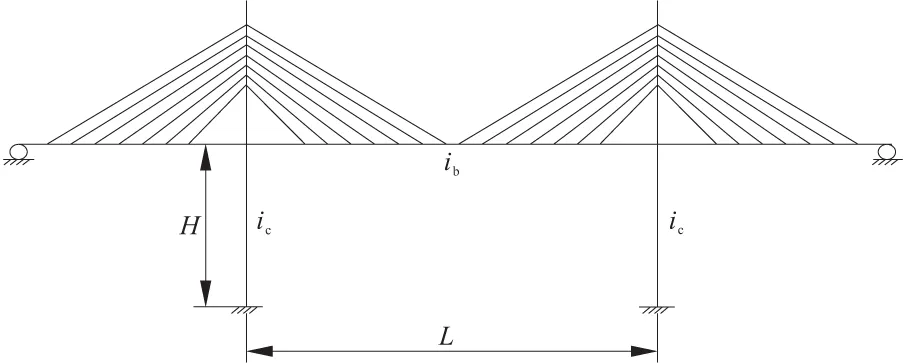
图1 斜拉桥的原始力学模型

将实际的斜拉桥结构简化为如图2所示的力学模型，即将边跨、上塔柱和斜拉索的结构几何部分省略。因斜拉索的重量相对较轻，忽略其重量，只考虑边跨主梁、中跨主梁、上塔柱和下塔柱的重量。图2模型中，参数定义如下：H为斜拉桥下塔柱的高度，即主梁顶部到下塔柱底部的距离(m)；L为斜拉桥的主跨(m)；mb为中跨主梁总质量的一半(t)；mc为一侧跨主梁与左塔柱的质量之和(t)；Ec为塔柱弹性模量(kPa)；Ac为塔柱截面面积(m2)；Ic为塔柱截面抗弯惯性矩(m4)；Eb为主梁弹性模量(kPa)；Ab为主梁截面面积(m2)；Ib为主梁截面抗弯惯性矩(m4)；塔柱轴向刚度jc=EcAc/H；塔柱弯曲线刚度ic=EcIc/H；主梁轴向刚度jb=EbAb/L；主梁弯曲线刚度ib=EbIb/L。

图2 斜拉桥的简化力学模型

将上图所示的门式框架模型等效为如下两个模型的叠加：正对称模型和反对称模型。由于荷载的反对称性，故正对称模型产生的地震力为零，这里分析反对称模型即可。

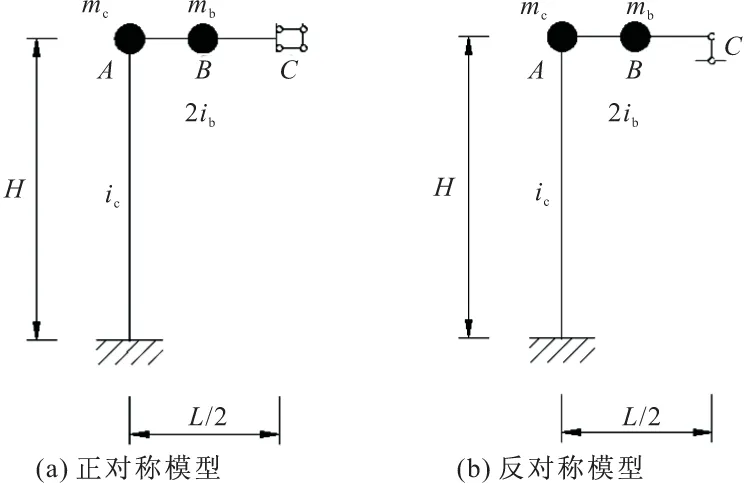
图3 正对称和反对称模型

1.2 振型向量的推导

这里分析反对称模型。假设主塔轴向刚度jc为无穷大，则在A节点上，节点质量mc有一个水平自由度和一个转角自由度；在B节点上，节点质量mb有水平、竖向和转动三个动力自由度；在C节点上，因竖向自由度为零，故只有水平和转动两个自由度。因此，A，B，C三个节点上共有2+3+2=7个自由度。对反对称模型节点的未知量进行编码，根据结构力学中的有限元分析原理，可组装集合得到结构总刚度矩阵K0(对称矩阵维度7×7)：

K0=

(1)

式中：第i行第j列元素kij表示仅使第j个自由度发生单位位移时，在自由度i上所需施加的外力。

结构总质量矩阵M0(矩阵维度7×7)为：

(2)

将式(1)(2)代入结构动力学中求解结构自振频率的通用公式|K0-ω2M0|=0求解。常系数ω2(ω为振动的圆频率)是高次方程式，且项次太多，解析式较复杂，考虑进一步简化。由于斜拉桥主梁的轴向刚度一般很大，故这里假设主梁轴向刚度jb=EbAb/L数学上无穷大，即忽略主梁轴向变形的影响，以便简化计算。此时，刚度矩阵K0便退化为K(对称矩阵维度5×5)：

(3)

对应的结构质量矩阵M0退化为M(矩阵维度5×5)：

(4)

第一阶振型对应的振型向量φ1定义为：

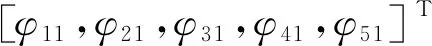
(5)

这里先求解矩阵φ1的部分元素φ11，φ21，φ51。假设主梁质量集中在墩顶，即墩顶质量为mc+mb，则刚度矩阵K进一步退化为K1(矩阵维度为3×3):

(6)

对应的结构质量矩阵M退化为M1(矩阵维度为3×3)：

(7)

根据结构动力学中求解自振频率的通用公式|K1-ω2M1|=0，可得频率ω满足下式:

(8)

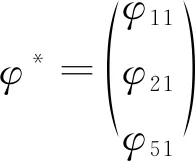
(9)

联立式(8)(9)，得到向量元素φ31为：

(10)

式中：φ11，φ21为A处的水平和转角振型坐标值；φ31，φ41为第一阶振型B处的竖向和转角振型坐标值；φ51为第一阶振型C处的转角振型坐标值。由于计算采用的是集中质量模型，故转角振型坐标值对下文计算剪力的贡献为零，不再求φ41。

1.3 一阶纵漂周期和塔柱剪力公式的确定

根据反应谱设计理论，且只考虑第一阶主要振型的影响，则斜拉桥桥塔剪力由下式确定：

F=kβ(T)γ1φi1Gi

(11)

式中：F为斜拉桥桥塔塔底剪力(kN)；k为地震水平加速度系数；β(T)为动力放大系数，动力放大系数按照下式确定：

(12)

式中：βmax为动力放大系数最大值；ω为结构的一阶自振频率；Tg为场地特征周期(s)。γ1为第一阶振型参与系数，按照下式确定：

(13)

式中：Gi为节点等效重量(t)； 由于转角振型向量对剪力贡献为零，因此φi1为第一阶振型在A、B处的各振型坐标值，即上节中的φ11，φ31。

引入“塔梁质量比”和“塔梁线刚度比”，具体定义如下：

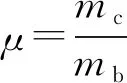
(14)

(15)

式中：塔柱弹性模量Ec和主梁弹性模量Eb的取值均由材料特性确定；对等截面的塔柱和主梁而言，塔柱截面的抗弯惯性矩Ic和主梁截面的抗弯惯性矩Ib均为常数，可通过截面特性分析软件计算得到；对变截面塔柱和变截面主梁而言，塔柱截面的抗弯惯性矩Ic和主梁截面的抗弯惯性矩Ib均不是常数，可通过等效刚度的原则来确定，此法也适用于等截面主塔和等截面主梁的情形。具体过程如下：

(1)将主塔简化为一端固定、一端自由的悬臂梁(变截面)；将主梁简化为两端固定的固结梁(变截面),见图4所示。

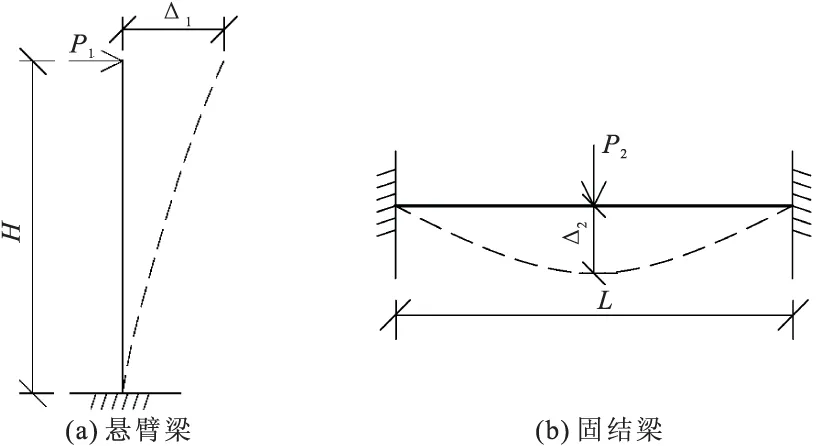
图4 悬臂梁和固结梁计算模型

(2)在悬臂梁的自由端施加荷载P1，在固结梁的跨中施加荷载P2；

(3)利用有限元软件建立数学模型，分别获得P1，P2作用下的自由端位移Δ1和跨中位移Δ2；

(4)按照下式确定塔柱的弯曲线刚度ic和主梁的弯曲线刚度ib。

(16)

(17)

将式(14)(15)代入式(8),得到一阶纵漂圆频率ω的最终公式：

(18)

则一阶纵飘的基本周期为

(19)

联立式(10)～(15)，得到桥塔剪力F的简化估算公式：

(20)

2 简化公式验证

为验证上述推导的简化公式的正确性和适用性，本文选取了四座塔梁固结体系斜拉桥算例进行对比分析，其有限元模型如图 5 所示。

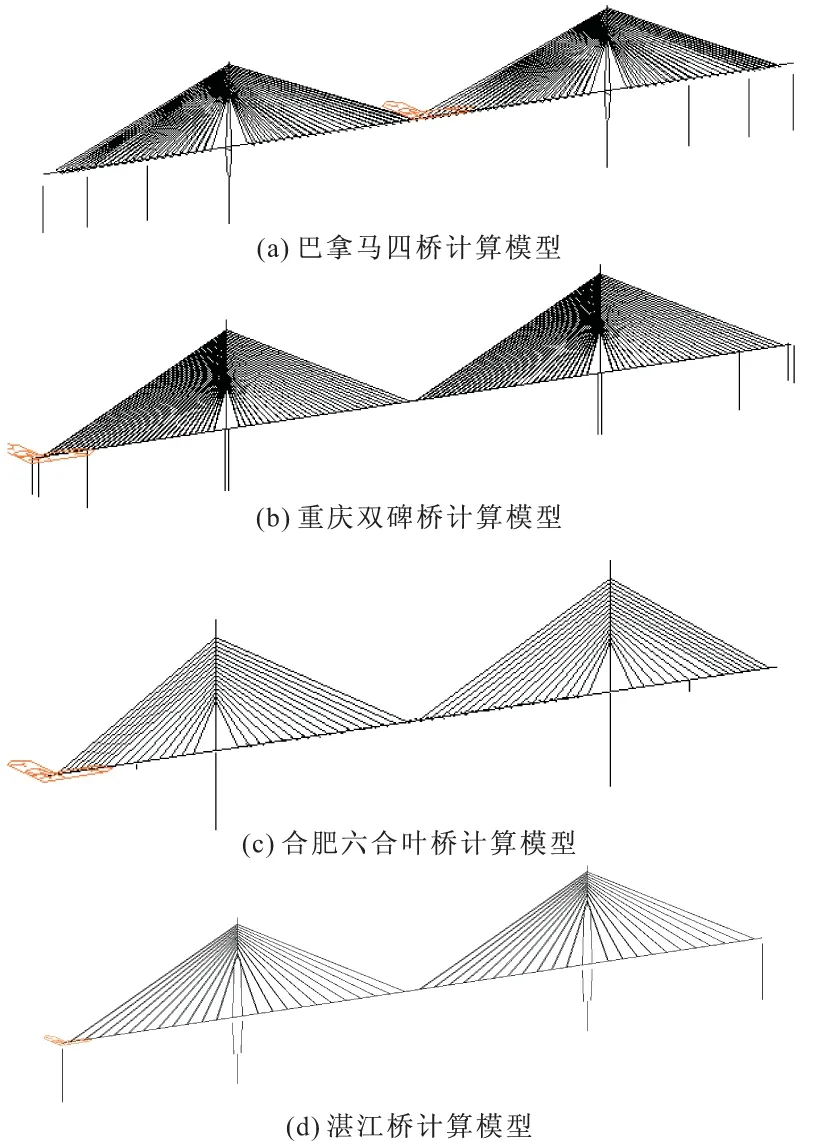
图5 有限元模型

公式所需的计算参数如表1所示，此外，βmax=2.25,k=0.2,Tg=0.4。

将计算参数代入公式进行求解，并和有限元结果进行对比，对比结果如表2，3。

表1 计算参数

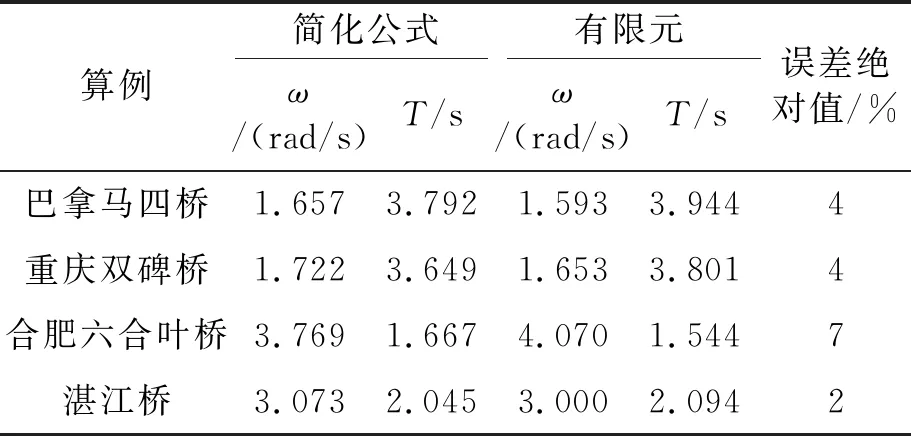
表2 一阶纵漂周期/频率结果对比

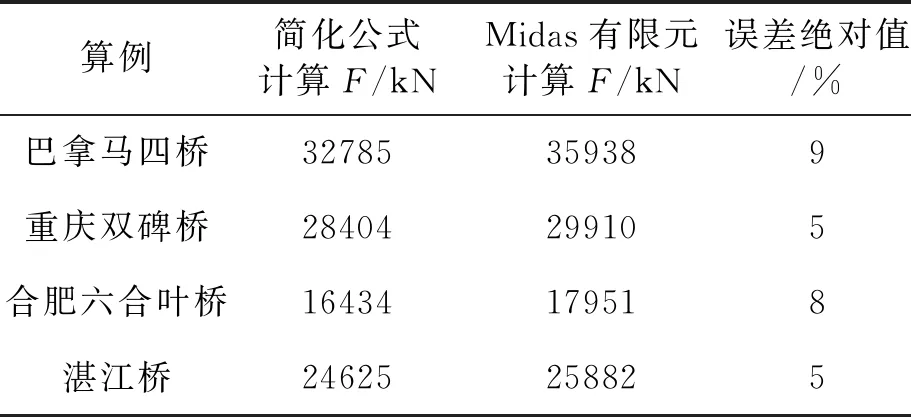
表3 桥塔剪力结果对比

从表2,3对比分析可以看出:简化公式和有限元模型计算得到结构一阶纵向振动自振周期误差在7%以内,桥塔的剪力误差在9%以内。

3 参数分析

现以巴拿马四桥为研究对象，对其桥塔地震剪力进行参数分析。函数F(μ,η)表达式为：

(21)

当ib，mb确定时，图6a为塔梁质量比μ固定时，桥塔剪力F随着塔梁线刚度比η的变化情况，可以看出，剪力F呈递增趋势。图6b与其变化趋势相同，但递增速度更快。为进一步观测两个参数对桥塔剪力的影响，将μ,η∈(0,10]时，函数F(μ,η)的变化绘制如图6c所示。由图可看出，F(μ,η)在两个方向均为单调递增趋势，最大值发生在点(10,10)处。在设计中，为了控制固结体系斜拉桥桥塔地震剪力，须优化塔梁质量比、塔梁线刚度比，以上结论具有一定参考意义。

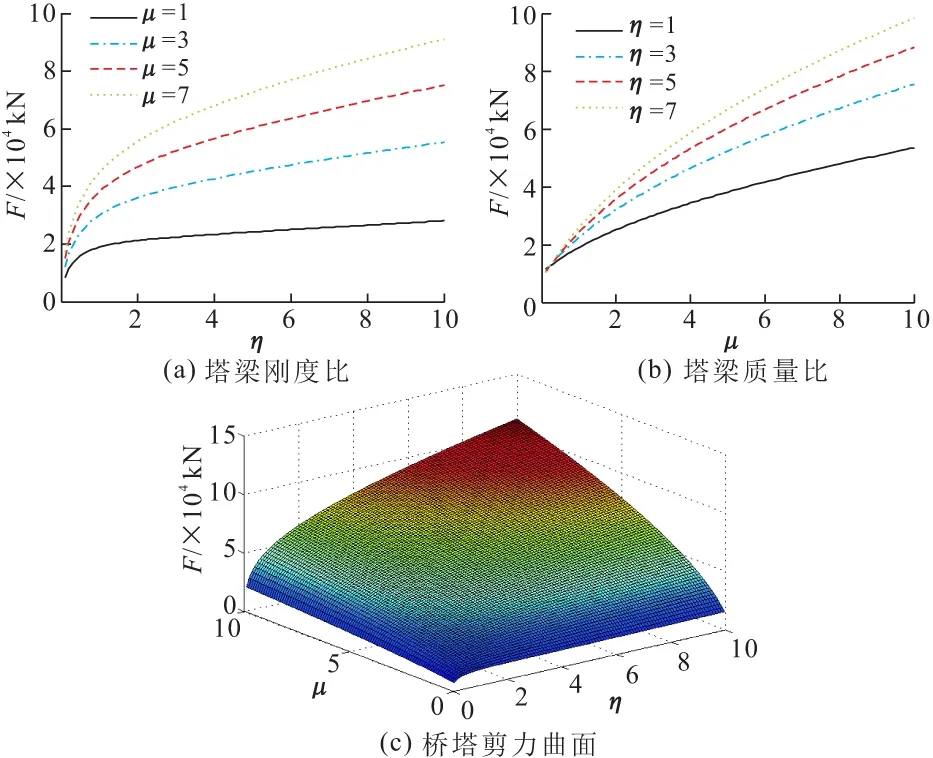
图6 参数分析

4 结 论

(1)基于力学原理，本文推导了固结体系斜拉桥一阶纵向振动周期和桥塔地震剪力的简化公式。该公式建立了结构地震响应与塔梁质量比和塔梁线刚度比的数学关系，能快速估算桥塔地震响应。利用本公式，可将繁琐的动力有限元试算问题转化为简单的理论公式求值问题，从而避免了大量的建模和数据分析工作，有效提高设计效率，可为固结体系斜拉桥抗震概念设计提供技术参考。

(2)结构一阶纵向振动周期简化公式和有限元计算结果误差在7%以内,桥塔剪力简化公式和有限元计算结果误差在9%以内，说明简化公式是实用可行的。

(3)桥塔地震剪力随着塔梁质量比、塔梁线刚度比增加时增加，在今后的桥塔抗剪设计中，合理选取这两个参数至关重要。