基于四元阵定位算法的鱼雷入水点误差分布分析

丁明惠, 庄 瑞, 岳 雷

基于四元阵定位算法的鱼雷入水点误差分布分析

丁明惠, 庄 瑞, 岳 雷

(昆明船舶设备研究试验中心, 云南 昆明, 650051)

鱼雷入水点精度是评定鱼雷性能的主要战技指标之一。文中首先推导了基于四元阵定位鱼雷入水点算法, 并进行了仿真验证。在此基础上, 针对由于时延差估计导致的定位误差进行了分析, 推导了其误差方程, 给出了误差较大部分的主要成因。最后对不同阵形的定位误差进行仿真, 并将引入同向误差和反向误差的仿真结果进行对比。结果表明, 通过改变原来正方形阵元的布放位置, 定位误差分布会向原正方形对角部分压缩, 并且误差较大的面积会减少, 从而达到了降低误差、提高定位精度的目的。文中研究可为四元阵测量鱼雷入水点工程应用提供参考。

鱼雷; 入水点; 四元阵; 误差分布

0 引言

火箭助飞鱼雷是水下反潜的主战武器之一, 其入水点精度对鱼雷射击效率有着重要的影响, 是火箭助飞鱼雷的主要技术指标[1]。类似的水中兵器还包括火箭助飞诱饵、拦截弹、深水炸弹等。传统测量鱼雷入水点主要依靠光测方式, 但该方式受环境限制较大, 而且有效作用距离不能满足试验需求, 因此, 只通过光测方式测量鱼雷入水点具有较大的风险[2]。

除了光测方式, 也可通过被动声呐进行入水点测量。被动声呐可采集鱼雷入水过程产生的瞬态信号, 通过数据处理实现对鱼雷入水点的定位[3]。目前常用的被动声呐基阵主要包括直线阵、“L”型阵、圆柱阵、平面四元阵、三角形阵等[4]。相对而言, 四元阵结构设计简单、阵元少、布放方便、成本不高, 广泛应用于被动测量领域[5]。四元阵定位鱼雷入水点系统是通过在估计入水点区域布放4个浮标, 浮标上包含差分全球定位系统(differential global positioning system, DGPS)、通信天线、水听器以及信号处理电路组件等, 对鱼雷入水信号进行采集并存储。由于原始信号数据量大, 若通过无线通信进行回传会给通信链带来很大的负担, 因此一般不进行实时处理, 而是待浮标回收后进行试后处理[6]。

关于四元阵定位目标问题, 文献[7]对四元阵的定位盲区进行了分析, 大部分盲区可在阵元布放过程中避免。文中对四元阵定位鱼雷入水点的算法和误差进行了分析, 提出可通过改变四元阵阵形方式改变误差分布, 从而提高定位精度。

1 四元阵定位入水点算法

1.1 数学模型

鱼雷在入水过程中产生的声信号为瞬态信号, 脉宽较小[8], 因此假设在产生声信号时间段内, 声源与浮标阵元的位置不随时间变化而变化。

1.2 入水点坐标解析表达式

将式(2)中的第2个方程与第1个方程相减并化简可得

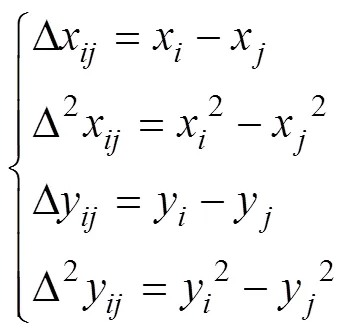
同时将式(2)中的第3个方程和第4个方程分别与第1个方程相减, 可得

令

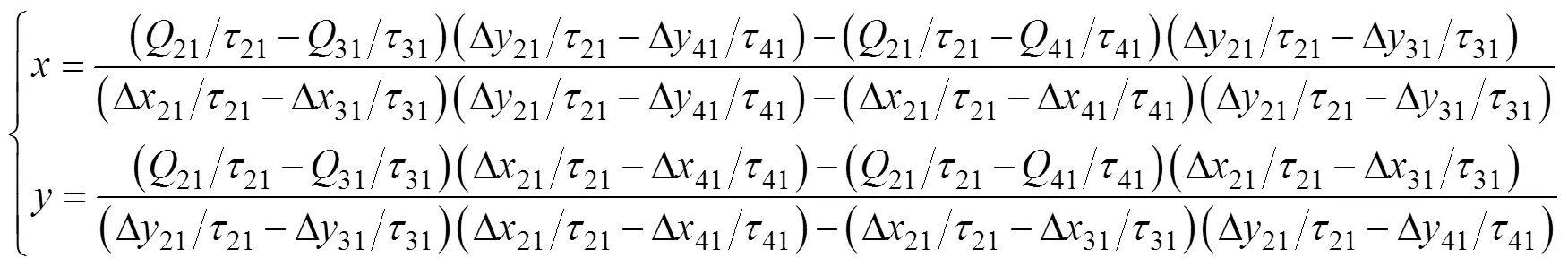
2 定位算法仿真

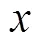
图2 误差分布图

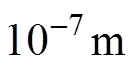
3 时延误差对定位误差分布影响分析

3.1 误差分析

影响定位鱼雷入水点误差与声速、浮标阵元位置以及时延差估计误差有关[9], 其中时延差估计的精度对四元阵定位误差影响最大[10]。

图3 引入0.5 ms同向时延误差的误差分布

图4 取对数后的误差分布

令

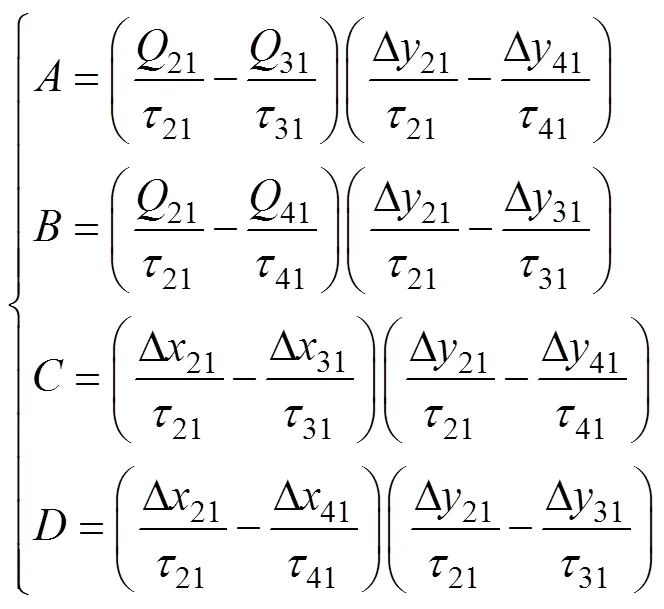
可得

经推导, 得

在工程应用中, 若鱼雷入水位置在误差较大区域, 会导致定位结果不具备参考性。

3.2 误差分布分析

仿真中, 对误差大于10 m的部分均按10 m处理来研究误差的分布情况, 仿真结果如图5所示。绝对误差不小于10 m为图中红色区域, 浮标阵元位置以圆形标注在图中。从图中可以发现, 误差不小于10 m的区域占据了浮标阵元中心十字位置。

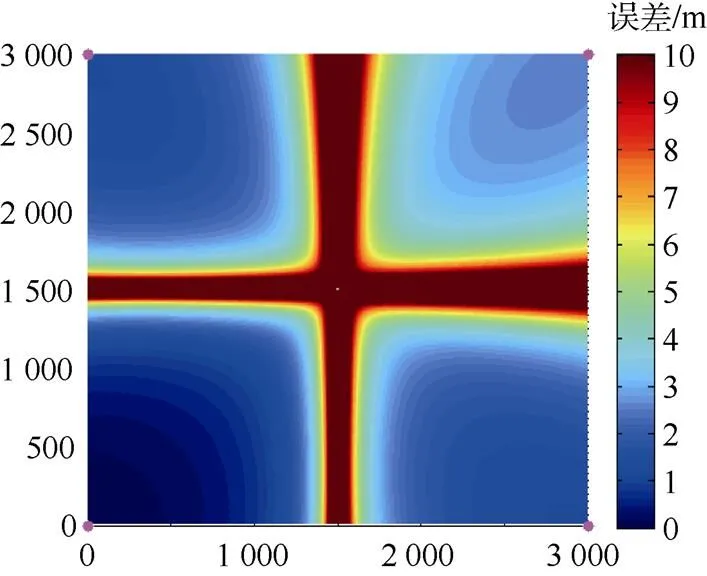
图5 误差大于10 m均记为10 m的误差分布

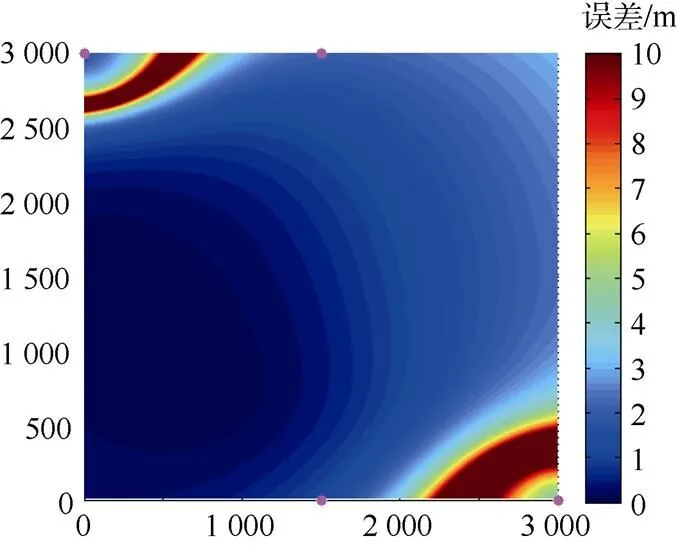
图6 阵形为平行四边形的误差分布

图7 缩短平行四边形上下边的误差分布

表1 不同阵形误差不小于10 m区域占总面积的百分比

通过仿真可以发现, 引入反向误差时, 大于10 m的误差区域面积比引入同向误差大; 在缩短平行四边形上下边时, 误差较大区域有压缩的趋势, 但通过使用该方法进行压缩误差较大区域时有一定的极限, 超过该极限会导致误差较大区域反弹增加。在进行其他的引入反向误差仿真, 会得到相同的结果, 文中不再赘述。

表2 不同阵形误差不小于20 m区域占总面积的百分比

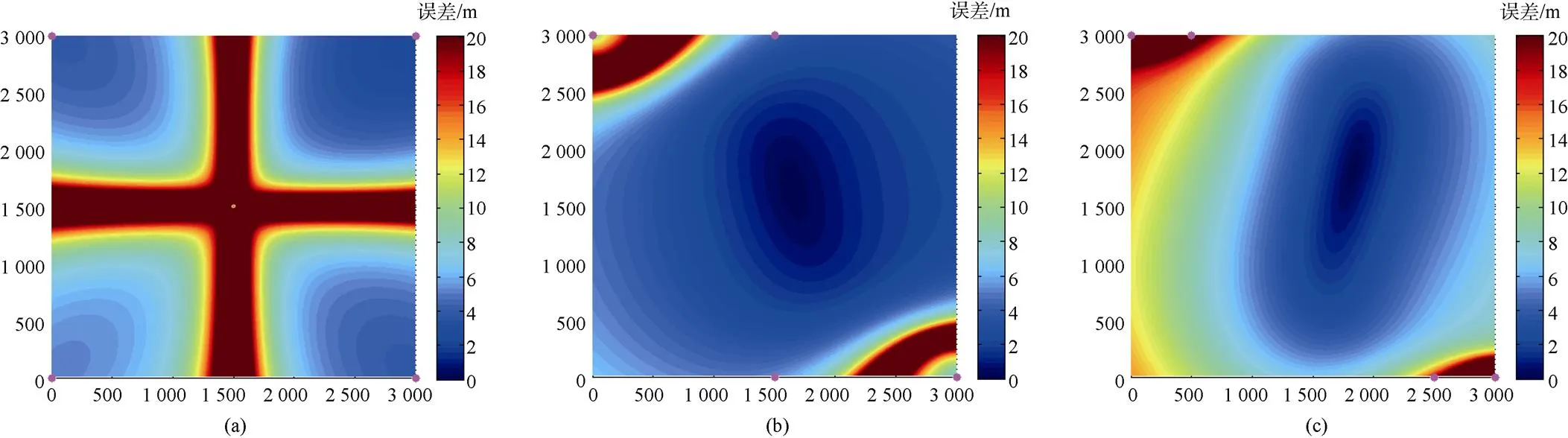
图9 误差大于20 m均记为20 m的误差分布

4 结束语

文中对四元阵被动定位鱼雷入水点的误差进行了研究, 对不同阵形的误差分布进行仿真分析, 并对引入同向和反向误差的仿真结果进行对比。仿真结果表明: 通过改变正方形一对角两阵元的布放位置, 定位误差分布会向原正方形无变化的对角部分压缩, 且误差较大的面积会减少, 从而达到了降低误差、提高定位精度的目的, 但超过一定的极限会导致误差较大区域反弹增加。当误差要求在10 m范围内时, 阵元坐标为(1 500, 0), (3 000, 0), (1 500, 3 000), (0, 3 000)会得到较好的误差分布, 误差不小于10 m区域面积占总面积的8.08%; 当误差要求在20 m范围内时,阵元坐标为(2500, 0), (3000,0), (500, 3 000), (0,3000)会得到较好的误差分布, 误差不小于20 m区域面积占总面积的1.87%。文中研究可为四元阵定位鱼雷入水点的工程应用提供阵元布放位置的理论参考。

[1] 宁永成, 侯代文, 邢国强. 火箭助飞鱼雷入水点精度评定方法[J]. 鱼雷技术, 2011, 19(2): 109-113.Ning Yong-cheng, Hou Dai-wen, Xing Guo-qiang. An Accuracy Assessment Method of Water Entry Point for Rocket Assisted Torpedo[J]. Torpedo Technology, 2011, 19(2): 109-113.

[2] 马锦垠, 侯宝娥. 火箭助飞鱼雷入水点测量系统的设计与实现[J]. 火力与指挥控制, 2012, 37(8): 199-201.Ma Jin-yin, Hou bao-e. Design and Implementation of Measuring System of Water Entry Point for Rocket Assisted Torpedo[J]. Fire Control and Command Control, 2012, 37(8): 199-201.

[3] 刘文海. 水下被动目标瞬态特征检测技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2010.

[4] 顾晓辉, 王晓鸣. 用双直角三角形阵对声目标定位的研究[J]. 声学技术, 2003, 22(1): 44-48.Gu Xiao-hui, Wang Xiao-ming. Location of Acoustic Target with Dual Right-triangles Array[J]. Technical Acoustics, 2003, 22(1): 44-48.

[5] Gao J, Deng J, Cai K. Study on Optimization and Performance of Four-element Acoustic Sensors Array[J]. International Conference on Intelligent Computation Technology and Automation. US: IEEE, 2011: 720-723.

[6] 李韦华, 薛飞, 马锦垠. 时延差双曲面定位方法在鱼雷入水点测量中的应用[J]. 鱼雷技术, 2015, 23(6): 420-422.Li Wei-hua, Xue Fei, Ma Jin-yin. Application of Localization Method Based on Time Delay Difference and Hyperboloid to Torpedo Water-Entry Point Measurement[J]. Torpedo Technology, 2015, 23(6): 420-422.

[7] 金磊磊, 马艳. 任意四元阵的定位盲区讨论及误差影响[J]. 探测与控制学报, 2015, 37(2): 90-94.Jin Lei-lei, Ma Yan. Discussion on Blind Area and Error Effect of Arbitrary Four-element Array[J]. Journal of Detection and Control, 2015, 37(2): 90-94.

[8] 吕成刚. 水下瞬态信号特性获取与分析[D]. 哈尔滨: 哈尔滨工程大学, 2009.

[9] 金磊磊, 梁红, 马艳. 基于水下无线传感器阵列网络多模态信息融合的目标定位[J]. 西北工业大学学报, 2017, 35(6): 1020-1025.Jin Lei-lei, Liang Hong, Ma Yan. Target Localization of UWSAN Based on Multi-Modal Information Fusion[J]. Journal of Northwestern Polytechnical University, 2017, 35(6): 1020-1025.

[10] 宋新见. 数字式噪声目标被动测距声呐研究[D]. 哈尔滨: 哈尔滨工程大学, 2004.

Analysis on Error Distribution of Torpedo Water-Entry Point Based on Four-Element Array Localization Algorithm

DING Ming-hui, ZHUANG Rui, YUE Lei

(Kunming Shipbuilding Equipment Research and Test Center, Kunming 650051, China)

The accuracy of torpedo water-entry point is one of the main tactical and technical indexes for assessing performance of torpedo. For localizating torpedo water-entry point by four-element array, a localization algorithm is derived and simulated in this paper. The error caused by delay difference estimation is analyzed. An error equation is derived, and the main factors leading to larger error are given. Moreover, the localization errors of different array formations are simulated, and the simulation results with co-directional error and reverse error are compared. It shows that the localization error distribution will be compressed to the diagonal part of the original square by changing the placement of four-element array, and the area with larger errors will be reduced. Thus, the aim of reducing errors and improving localization accuracy is achieved.

torpedo; water-entry point; four-element array; error distribution

TJ630.33

A

2096-3920(2019)06-0658-06

10.11993/j.issn.2096-3920.2019.06.009

丁明惠, 庄瑞, 岳雷. 基于四元阵定位算法的鱼雷入水点误差分布分析[J]. 水下无人系统学报, 2019, 27(6): 658-663.

2019-03-16;

2019-04-03.

丁明惠(1986-), 男, 硕士, 工程师, 主要研究方向为水声信号处理.

(责任编辑: 许 妍)