数感分析:数学解题思路的分析方法*
2020-01-07蒋双赵思林
蒋双 赵思林
摘 要:数感是数学核心素养的核心成分.数感分析有利于发现解题的思路或结论.数感的产生依赖于丰富的经验、敏锐的眼光、灵活的思维.因此,数学解题是培养数感的重要资源.
关键词:数感;数感分析;高考试题;解题思路
数感是数学教学的核心目标,是数学素养的集中体现.数感分析在解题思路发现过程中占有重要地位.数感是以“数概念”在人脑中的扩展而产生的一种对数学问题的敏感,是一种对数字(量)的直觉,是一种敏捷的感知[1].詹国棵[2]认为:“狭义的‘数感是指‘数字感,它的含义是指人脑对于数字或数字运算的直觉,即对于‘数字或数字运算的洞察与领悟;广义的‘数感是指对‘数学的感觉,即人脑对数学对象的直觉,亦即对于数学对象的洞察与领悟.”在这里,狭义的“数感”忽视了数学中除“数”之外的另一半——“形”.因为数学的研究对象是“数”和“形”,所以只研究“数”的数学是不全面的.在初中,学生就知道“实数与数轴上的点构成一一对应关系”,即是说,初中生都知道,数学包括“数”和“形”.所以广義的“数感”更全面、更合理、更有用.数感可谓五味俱全,它含有“感觉”“直觉”“直感”“洞察”“经验”“灵感”等多种成分.研究者认为,数感是对数学对象(问题)的敏感(敏捷感觉),这里的数学对象可以是代数式(包括数字)、数学符号、图形、数学关系(定理、公式、性质等)、数学模型、问题情境、“数”与“形”及其混合体等.数感分析是指从数感的角度探索数学问题求解题思路的一种分析方法.数感分析高度依赖于原型、直观、直觉、猜测、想象等数学经验.数感分析有利于发现解题的思路或结论.数感是数学核心素养的精华成分.培养数感就是在培养数学核心素养,数学解题是培养数感的重要资源.
一、对特殊“数字”的敏感
例1 (新高考卷Ⅰ第2题)[2-i1+2i]=( ).
A.[ 1] B .[-1] C. [i] D .[-i]
评析:本题出现在选择题第2题,一般属于容易题,可考虑借助于数感,通过心算简单获解.
思路1:从选项获数感,4个“答案”都简单,可采用逐一检验的方法.显然A、B不成立.对于C,只需计算[(1+2i)×i=i-2],这与分子不相等,所以C错.故选D.
思路2:从“化简‘分式的基本方法是‘约分”获得数感,[2-i=-2i2-i=-i(2i+1)],约分后即得答案[-i],选D.
说明:数感依赖于经验.若没有观察“答案”、化简“分式”的基本方法是“约分”等经验,则上述两种思路是不易想到的.
例2 (全国卷Ⅲ理第12题)已知55<84,134<85,设a=log53,b=log85,c=log138,则( ).
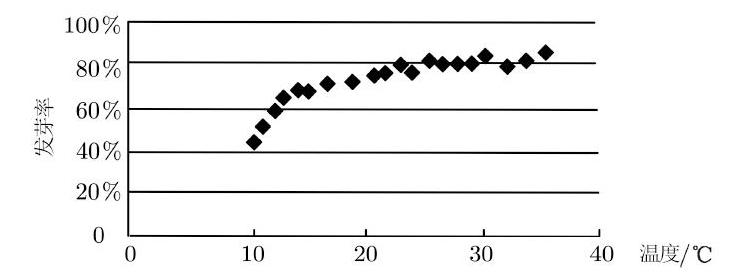
A. a 评析:据了解,很多考生不明白给出的两个条件55<84,134<85,到底有何意图.其实,设计这两个条件的意图有三:一是为降低题目难度,或有提示解法之意;二是需要把指数不等式变成对数不等式,才便于利用对数这个工具;三是希望考生能从这两个不等式的指数“感觉”到“[45]”(比较大小的“媒介”)的存在,这个“[45]”正是数感的产物. 二、对“数学模型”的敏感 例3 (全国卷Ⅰ理第5题)某校一个课外学习小组为研究某作物种子的发芽率[y]和温度[x](单位:[℃])的关系,在[20]个不同的温度条件下进行种子发芽实验,由实验数据[(xi,yi)][(i=1,2,…,20)]得到下面的散点图. 由此散点图,在[10℃]至[40℃]之间,下面四个回归方程类型中最适宜作为发芽率[y]和温度[x]的回归方程类型的是( ). A.[ y=a+bx] B.[ y=a+bx2] C.[ y=a+bex] D.[ y=a+blnx] 评析:从散点图可发现,当温度达到[20℃]后其增长速度是缓慢增长,这恰好与对数函数图象的模型比较吻合.再结合四个选项,容易选D. 说明:学生应知道,4个“答案”的函数模型分别代表线性增长、抛物增长、爆炸增长、缓慢增长. 例4 (全国卷Ⅱ理第11题)若2x-2y<3-x-3-y,则( ). A. ln(y-x+1)>0 B. ln(y-x+1)<0 C. ln[x-y>0] D. ln[x-y<0] 评析:借用“合并同类项”的经验(式子感),把原不等式化为[2x-3-x<2y-3-y],由此可构造一个新的函数[f(x)=2x-3-x],则有[f(x) 三、对“图形”的敏感 例5 (全国卷Ⅰ理第14题)设[a,b]为单位向量,且[a+b=1],则[a-b=]________. 评析:本题的条件有三个:[a=1],[b=1],[a+b=1].如果再把[a-b]考虑在内,则本题共涉及4个模,即4个长度(距离).因此,从模的几何意义考虑问题是自然的、简单的想法.若把上述三个条件赋予几何意义,则可以[a,b]为邻边作一个平行四边形.再由三个条件易知,此平行四边形必为菱形,且[a,b]的夹角为[120°].又[a-b]恰好是这个菱形的另外一条对角线,因此,[a-b=3]. 若学生熟悉恒等式[a+b2+a-b2=2a2+2b2],则此题可心算获解. 例6 (全国卷Ⅰ理第11题)已知[⊙M:x2+y2-2x-2y-2=0],且直线[l:2x+y+2=0], [P]为[l]上的动点,过点[P]作[⊙M]的切线[PA],[PB],切点为[A],[B],当[PA?PB]最小时,直线[AB]的方程为( ). A.[ 2x-y-1=0] B.[ 2x+y-1=0] C.[ 2x-y+1=0] D.[ 2x+y+1=0] 评析:本题若直接着手于“算”的话,则不易找到思路,并且比较麻烦.但若对相应的图形的几何意义产生数感,则问题的解决思路会油然而生. 将圆化为标准方程[(x-1)2+(y-1)2=4],得圆心M(1,1), [r=AM=2].由面积法可得, [S四边形PAMB=AM?PA=2PM2-4]. [PM]取最小值[?][PM⊥l][?AB//l],即可排除A和C.故选D. 四、对“数学经验”的敏感 例7 (全国卷Ⅱ理第6题)数列[an]中,a1=2,am+n=aman,若[ak+1+ak+2+…+ak+10][=215-25],则k=( ). A. 2 B. 3 C. 4 D. 5 评析:符号多是本题的一大特色,这也让考生感到像“雾里看花”,并产生无从下手的感觉.这正好体现本题考查学生的高级认知(分析、猜测、洞察、演绎等)的真实意图.由数据[215, 25]可强烈地感受到该数列可能含有等比数列的信息,这就是数感.递推方程[am+n=][aman]是一个一般性的递推关系,考生需要从这个关系中敏锐地发现并构造出含通项[an]和它的后一项[an+1]的递推关系,才有可能用到等比数列知识.因此,采用特殊值法,取[m=1],则[an+1=a1an].又因为[a1=2],所以[an+1an=2],因此[an]是等比数列,则[an=2n]. 所以[ak+1+ak+2+]…[+ak+10][=2k+1(210-1)] [=2k+11-2k+1=215-25].故选C. 五、对“数学美”的敏感 “化丑为美”是数学解题的基本策略.解高考数学题要善于把丑的形式(结构)化为美的形式(结构). 例8 (全国卷Ⅱ第21题)已知函数[f(x)=sin2xsin2x]. (1)讨论[f(x)]在区间[0, π]的单调性; (2)证明:[f(x)≤338]; (3)设[n∈N*],证明:[sin2xsin22xsin24x…] [sin22nx≤3n4n]. 评析:第(1)题是常规题,其解析从略. 第(2)题因为函数[f(x)]是奇函数,所以只需证明[f(x)]的最大值是[338]. 因为在[f(x)=sin2xsin2x]中的次数不同、角度不同,因此该结构是最简的,但不是最美的.作降次變换得,[f(x)=sin2xsin2x=1-cos2x2?sin2x=14(2sin2x-sin4x)]. 记[p(x)=2sin2x-sin4x],此式右边两项的系数分别是[2, -1],因此,[2sin2x-sin4x]的形式仍然是不美的(不对称).但若先变形为[p(x)=sin2x+sin2x][+sin(2π-4x)];再作换元,即令[2x=A, 2x=B],[2π-4x=C],则[A+B+C=2π],且[p(x)=sinA+][sinB][+sinC].此形式显得简单了、美了.从而,可借助于以下结论求出[p(x)]的最大值. 结论:在[△ABC]中,[sinA+sinB+sinC]在[A=B=C=π3]时取得最大值. 这个结论的条件和结论都体现对称美和简单美.此结论在一些书籍上有,其发现和证明过程均可掌握[3].这个结论是产生数感的“原型”. 借助上述结论,其思路探索和解答就容易了.事实上,由[sint]在[0, π]上的上凸可得, [p(x)=sinA+][sinB]+[sinC ][≤][ 3sinA+B+C3] [=3sin2π3=332]. 所以[f(x)=14p(x)≤338].以下从略. 第(3)题的证明,[sin2xsin22xsin24x…sin22nx] [=(sin3xsin32xsin34x…sin32nx)23] =[sinx ][(sin2xsin2x)·(sin22xsin4x)]… [(sin22n-1xsin2nx)][sin22nx][23] =[sinx·f(x)·f(2x)·f(2n-1x)] ·[sin22nx][23] [≤f(x)?f(2x)…f(2n-1x)23]. 下面反复用第(2)题的结论进行放缩即可,从略. 重视数感的培养无疑是重要的和必要的.已有数感经验是产生新数感的基础.数感的经验源于对数感的实践、反思与凝练.数感是数学核心素养的核心成分,数感的产生依赖于数学核心素养的生成,即数感的产生依赖于丰富的经验、敏锐的眼光、灵活的思维.数感的实质就是能用数学眼光对情境(问题)的快速审视并顿生感觉.用数学的眼光看问题,就是要“想看”“会看”“看思结合”,“看出来的感觉”即为数感.在新课教学中,数感的培养可以从知识产生、发展、发现的过程着手培养.数学解题教学是培养学生数感的沃土,教师不宜让学生急忙着手去算,而是应先让学生对问题进行仔细观察、直觉分析、整体把握、思路预估等思维活动,因为这可达到多角度、多层次培育数感的目的. 参考文献: [1]叶蓓蓓.对数感的再认识与思考[J].数学教育学报,2004,13(2):34-36. [2]詹国棵.数感的内涵[J].苏州教育学院学报,2005,22(1):69-71. [3]赵思林,卢勇刚,李雪梅.对一道以核心素养立意的高考数学试题的探究[J].教育研究与评论,2019(1):64-69.
