物理教学中的归纳推理策略

刘伟

摘    要：作为科学推理的重要构成，归纳推理是得出结论的基本途径.在事物基本属性的归纳和推断、基本规律的总结和提炼中，合理的推理不仅能优化知识的形成，实现对新知识的同化和迁移，而且能更本质地内化过程遵从的一般规律，积淀更丰富的解题策略，从而提升学生的科学思维.

关键词：科学推理;归纳推理;科学思维

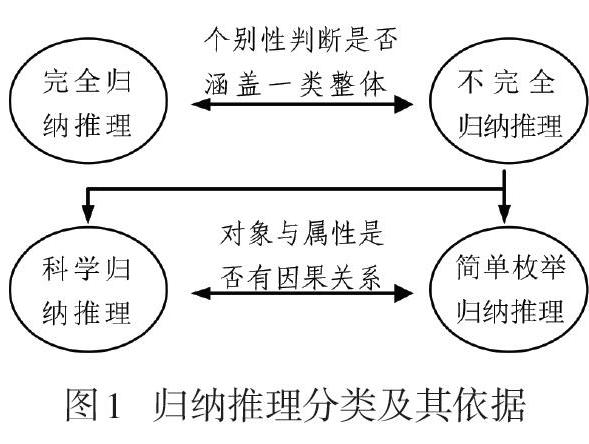
《普通高中物理课程标准（2017年版）》要求“让学生在观察、实验的基础上通过科学推理和科学论证等得到结论” [1].作为科学推理的重要构成，归纳推理是得出结论的基本途径，它是以个别性或特殊性知识为前提，提出一般性知识（概念、规律、原理）为结论的推理.如图1所示，依据个别性判断是否涵盖某类整体，归纳推理区分为完全归纳推理和不完全归纳推理;又依据对象与其属性间是否存在必然联系，把不完全归纳推理进一步细分成简单枚举归纳推理和科学归纳推理.

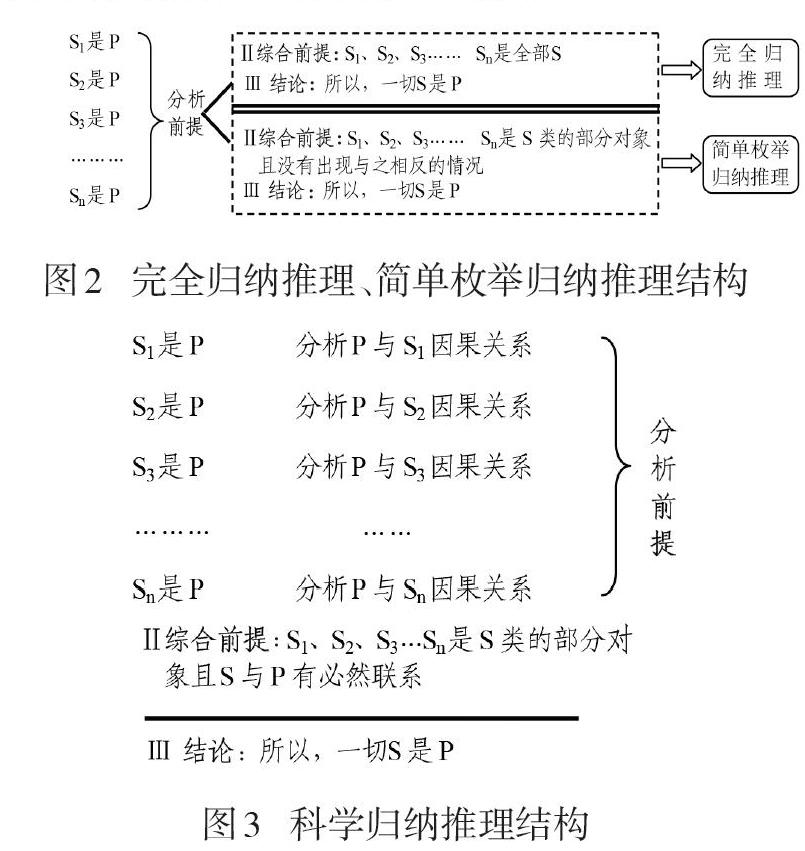
一般而言，归纳推理由分析前提、综合前提和结论三部分组成.其中完全归纳推理与简单枚举归纳推理在结构上比较接近，只在综合前提部分的断定上有区别：前者个别性判断涵盖了一类事物的整体;后者个别性判断则是一类事物的部分对象，同时要求已作的个别性判断没有反例出现，如图2所示.科学归纳推理可以看成是简单枚举归纳推理的发展，但结构相对复杂，不仅需要在综合前提中判断对象与属性间的必然联系，而且要逐项对分析前提部分作此判断，图3为其推理结构.

我们知道，三类归纳推理推知的都是一般性结论，科学概念和规律就是一般性知识，因此归纳推理是学生获取新知识的基本来源.下面就结合教学谈谈笔者的实践思考.

一、辨析概念关系   审视结论科学性

教学中教师很少会有意识地让学生经历一个完整的推理过程，即便经历该过程的某些阶段，也会因为逻辑应用上的偏差，导致过程的不科学，由此而来的推断也就不可靠了.以完全归纳推理为例，该推理的前提考察了一类事物的全部对象，断定了该类每一对象具有（或不具有）某种属性，结论断定的是整类事物具有（或不具有）该属性[2]101.其结论断定没有超出前提断定的范围，因此只要前提真实形式有效，结论得出是必然的.

值得注意的是，逻辑学中概念间的关系是根据外延间关系来确定的，完全归纳推理的结论必须是全称判断，即结论与分析前提中个别判断的主项必须是属种关系，而不是整体与部分的关系[3].实际推理过程中，有时单独判断前提和结论都是正确的，但因未厘清两者概念间的关系，会导致推理过程的错误.

案例1   归纳核子数、原子核数与质量比之间的数量关系

Ⅰ.分析前提：原子核内质子数等于质子总质量与碳原子质量[112]之比取整数（真）.

原子核内中子数等于中子总质量与碳原子质量[112]之比取整数（真）.

Ⅱ.综合前提：原子核内质子数、中子数是原子核的全部核子数.

Ⅲ.结论：所以，原子核数等于原子核质量与碳原子质量[112]之比取整数（假）.

【案例分析】推理中，我们先对核子情况逐一考察，判断每一场合都具有核子数等于该核子总质量与碳原子质量[112]之比取整数，在确认已穷举全部核子的情形下，推导出“原子核数等于原子核质量与碳原子质量[112]之比取整数”的结论却是错误的，原因在于结论中的“原子核”与分析前提中的“质子”“中子”是整体与部分的关系，而非属种间的包含关系，推理逻辑上出现了问题.而且，综合前提中的“原子核的全部核子”与“原子核”也不是同一个概念，类似这种推断是常见的错误情形，正确的结论应该是“核子数等于原子核质量与碳原子质量[112]之比取整数”.

由此，教学中在掌握推理结构的基础上，我们要进一步指导学生明确结构各部分间的逻辑关联，在归纳过程中要求学生审视结论与个别判断主项间的概念关系.同时加强推演结论的专项训练，形式上可以组织学生在课堂上共学，学生之间互练，也可以安排纸笔练习集中突破.需要指出的是，完全归纳推理结构虽然简单，但在严格的科学推理论证中却常常被用于推断正确的一般性论断.

二、研判前提真假   审思结论合理性

归纳推理的前提必须是确凿的事实，如出现一个假判断，就可能得到错误结论，这是由归纳推理自身性质及特点决定的，也是与演绎推理的不同之处.教学实践中，为了增加解题思路的指向性，提高效率和准确率，教师通常会指导学生反思解题进程，归纳策略技巧，提炼二级结论.这个提炼过程其实就是简单枚举的推理过程.

以简单枚举归纳推理为例，该推理根据一类事物中部分对象，具有（或不具有）某种属性，而没有遇到相反情况，结论推出整类事物具有（或不具有）某种属性的推理.由于简单枚举归纳推理只是考察了事物的现象，没有进一步分析现象产生的原因，未研究事物的本质，而且结论断定又超出了前提断定范围，即便已考察对象没有相反情况出现，也并不代表该类中不存在相反情况[4]21.所以，它只能做出或然性结论，而提供不了必然性论断.当然，考察对象越多，结论就会更合理更可靠.

案例2   归纳异形单摆周期公式中等效重力加速度g效的表达式

比照标准单摆（单摆系统处于单一重力场及惯性参考系）周期公式T=2[π][lg]中的重力加速度g，以确定等效重力加速度g效的表达式.设摆球静止时摆线拉力F，摆球质量m，则带电摆球的单摆系统有                 .

Ⅰ.分析前提：置于恒定加速度環境中，摆球再受到大小不变的力，有g效=[Fm]（真）.

置于匀强电场中，摆球再受到大小不变的力，有g效=[Fm] （真）.

置于悬点处点电荷电场中，摆球再受到大小不变的力，有g效=[Fm]（假）.

Ⅱ.综合前提：恒定加速度环境、匀强电场、悬点处点电荷电场中，带电摆球再受到大小不变的力且没有出现与之相反的情况.

Ⅲ.结论：所以，一切摆球再受到大小不变的力，有g效=[Fm] （假）.

【案例分析】单摆置于悬点处点电荷电场中，带电摆球受到的库仑力沿摆线方向，对摆球在振动方向上的回复力没有贡献即g效=g，因此摆球运动周期并没有改变，正因为前提中包含了假判断，因而结论就是假的.类似只根据少数表面现象就轻率地做出一般性的结论，在逻辑上犯了“轻率概括”或“以偏概全”的错误.

事实上，简单枚举推理在科学研究中发挥着重要的作用，特别是初步研究阶段，我们并不能在短时间内为某些现象找到充分概括的根据，这时就得先根据简单枚举归纳推理概括出一个初步的假定，然后再逐步寻找根据，发现其规律性，证实或推翻这个最初的假定[2]102.这种归纳在教学中应用广泛，譬如在光本性的探索中，托马斯·杨、菲涅耳、马吕斯等分别观察到了光的干涉、衍射和偏振现象，据此断定光是一列波，但光电效应和康普顿效应的反例否定了光只是一列波的论断.又如人教版必修一《实验：探究加速度与力、质量的关系》一节渗透并应用了该推理的思想：由实验数据作图猜测a∝F，a∝[1m]→多次完成类似实验，发现都存在相似结论→根据这些结论推导出的很多新结果都与事实一致→结论上升为“定律”.

我们体会到，如果学生缺乏必要的生活体验，教师又不能提供适宜的感性素材，要让学生充分理解抽象结论是比较困难的.这启示我们教学中要重视概念和规律首次构建过程，使学生对概念、规律形成清晰的理解;善于引导学生辨析知识点间、知识组块间的区别与联系，暴露学生的思维进程，切不可直截了当给出结论.与此同时，教师一方面要指导学生审视反思过程的严谨性，另一方面也要为学生反思结论进行把关，增加可靠性，还要结合实例教给学生一些归纳推理的逻辑知识，进而提高结论的合理性.

三、施行分步归纳   审度结论严谨性

一些场景蕴含的一般性结论比较抽象概括，特别是涉及了多元情形、牵涉到多个物理量、关联了多类归纳推理形式时，学生头脑中不易形成正确的表象，为此教师引导学生顺利归纳成为一个难点.教学中如何有序呈现事实，如何铺设具体化归纳情境，如何引导学生分散难点、分步归纳、形成严谨的结论，就尤为重要，而科学归纳推理往往在其中起到重要作用.科学归纳推理需先根据前提断定一类事物的部分对象是否具有（或不具有）某种属性，并分析这部分对象和属性间的必然联系，从而断定这一类事物的一般性结论.

关于科学归纳推理结论的真实性存有争议，目前更多认同或然性，主要原因是结论的断定超出了前提断定的范围.但与简单枚举归纳推理对事物经验的重复判断不同，科学归纳推理深入进行科学分析，以认识因果关系、本质联系为根据，因此结论高度可靠[4]21.更需一提的是，这种可靠性与前提中断定的个别对象的数量无关，因此不需要列举大量对象，有时甚至只根据一个典型事例，就可以做出正确的结论[4]22.在科学发展中，许多科学结论都是在观察、实验等认知材料的基础上，运用科学归纳推理的结果.

案例3   归纳“楞次定律”

该案例采用分步归纳的方式.

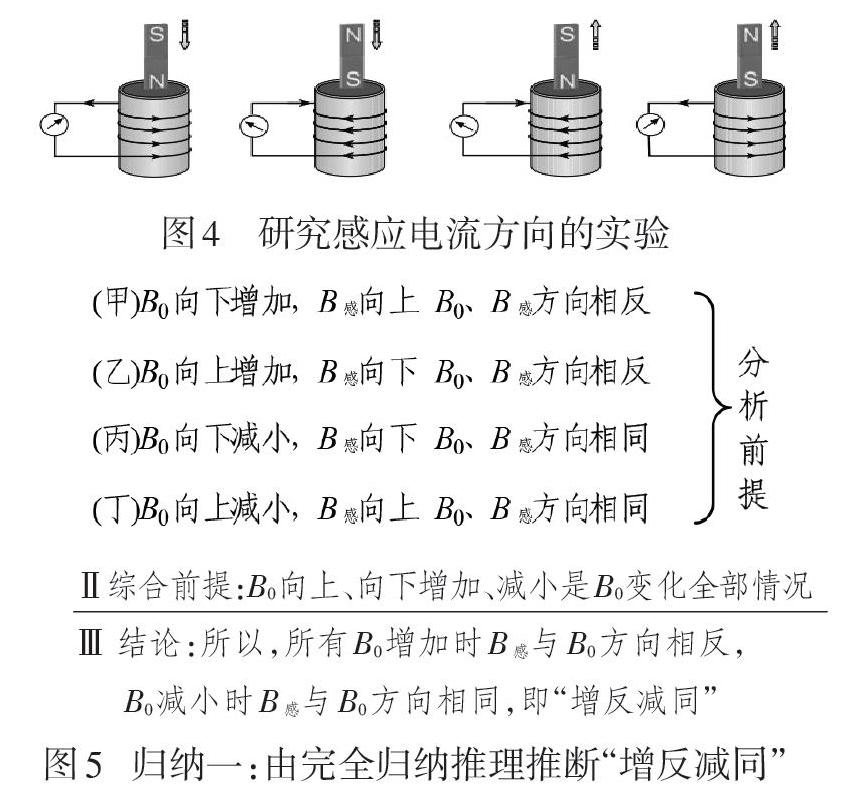
1.记录如图4研究感应电流方向的实验结果，梳理因果关系，把原磁场、感应电流磁场、原磁通变化分别记为B0、B感、[Δ]φ0.如图5，归纳一：由完全归纳推理推知，B0在某方向增加时，B感方向与B0方向相反;减小时相同，即“增反减同”.

Ⅱ综合前提：B0向上、向下增加、减小是B0变化全部情况

Ⅲ 结论：所以，所有B0增加时B感与B0方向相反，

B0减小时B感与B0方向相同，即“增反减同”

2.进一步推断B感方向的规律.如图6，归纳二：个别判断的B感方向与“阻碍”属性之间的因果关系，由科学归纳推理推知，B感总要阻碍[Δ]φ0，从而得出“楞次定律”.

【案例分析】在探寻B0、B感与[Δ]φ0之间关系时，学生会发现物理量间没有简捷直接的对应关系，因此教师要引导呈现利于归纳的情境，进行分步归纳：一是引入既与B0方向及大小变化（[Δ]φ）有关又与I感有关的“中介量B感”，通过完全归纳推断“增反减同”;二是建立B感的方向通过抵消或弥补来延缓[Δ]φ0的必然联系，并由科学归纳断定B感总要阻碍[Δ]φ0.

归纳推理尤其是科学归纳推理过程本质上是概念、规律发生和得出的过程，契合了学生认知的渐进发展，因此如何引导学生参与其中，亲身得出结论，理应是教学设计和实施的关键.依据事物的不同情境，实际教学中我们可以通过让学生口述事例、“出声思维”、自主实验，教师推演关键过程、多媒体展示、实验演示等来呈现个别化对象与过程.在正确评估归纳难度基础上，若需要学生自主提炼，那么不同事物的共同属性应突出一些;若是借助教师的协助，那么规律可以更隐含抽象一些.教师若能有意识地让学生自主（或引导学生）形成概念、提炼规律，不仅能促使学生更好地理解知识，更重要的是能促成归纳推理能力的提高.

总之，三类归纳推理在学生获取新知识、拓展认知范围上都是极其重要的.因此，在事物基本属性的归纳和推断、基本规律的总结和提炼中，合理的推理不仅能优化知识的形成，实现对新知识的同化和迁移，而且能更本质地内化过程遵从的一般规律，积淀更丰富的解题策略，从而提升学生的科学思维.

参考文献：

[1]中华人民共和国教育部. 普通高中物理课程标准（2017年版）[M].北京：人民教育出版社，2018：51.

[2]刘邦凡，何向東.认知科学视域下的归纳逻辑研究述评[J].逻辑学研究，2014（1）.

[3]李衍华.正确进行归纳推理的条件及结论的性质[J].北京师范大学学报，1983（12）：17-19.

[4]苏俊华.科学教学中培养初中生推理能力的研究[D].温州：温州大学，2017.