致密储层脆性测井解释方法研究

2020-01-07覃豪杨小磊

测井技术 2019年5期

覃豪,杨小磊

(大庆油田公司勘探开发研究院,黑龙江大庆163712)

0 引言

随着水平井和体积压裂改造技术的突破,致密油气已经成为现实接替领域[1]。致密油气储层的“三品质”是致密储层测井评价的核心,其中工程品质,是选择压裂层段、能否充分解放致密储层的油气潜力的基础[2]。工程品质评价最终的目的是评价储层的脆性。岩石脆性指数反映岩石易于破裂程度,是致密油储层体积压裂设计中的重要参数,一般采用弹性参数计算或矿物组分法计算[3-7]。

大庆深层徐家围子地区沙河子组致密储层与优质烃源岩相接触,是典型的致密气储层。该区储层岩性为长石岩屑砂岩和岩屑长石砂岩等,命名达到20余类,长石种类包括钾长石和斜长石,岩屑种类包括变质岩和岩浆岩,杂基种类包括泥质和方解石。当岩石的矿物含量相同,储层分选、胶结类型和粒度等发生变化时,选择合适的方法对储层的脆性进行准确解释,是应用测井方法评价脆性的核心,均须开展研究。本文通过对矿物组分法和弹性参数法进行深入分析和评价,指出这2种方法解释脆性的关键技术;并假设地层为块状均质条件下,采用理论计算的方法,分析脆性随岩石物理特征变化而变化的规律;选择弹性参数法解释该区沙河子组的致密储层脆性,为致密气勘探开发提供了可靠保障。

1 脆性评价方法

1.1 矿物组分法

常用脆性评价方法是北美油页岩矿物组分法,其表达式见式(1)。从式(1)可知,矿物组分法关键是确定各类造岩矿物的体积含量。目前各类矿物含量解释的方法有最优化法[8]和统计回归法等。北美油页岩,岩性主要为碳酸盐岩,其矿物种类相对简单,应用这2种方法解释的矿物体积,相对比较准确。中国的致密储层一般为陆源碎屑沉积的岩石,在应用矿物组分法时,一般对式(1)进行变形优化,变形后的计算模型见式(2)。应用式(2)解释研究区的脆性,关键是主要脆性矿物含量的解释。

(1)

(2)

式中,IB为脆性指数,无量纲;Vqa、Vca、Vfd、Vdo和Vcl分别为石英、方解石、长石、白云石和黏土的体积含量,%。

研究区多产长石岩屑砂岩或岩屑长石砂岩,岩屑类型一般为岩浆岩、变质岩(薄片资料),对于变质岩和岩浆岩的矿物类型无法从薄片等资料明确,因此,无法确定致密砂岩中的岩屑是否为脆性物质,也无法确定岩屑中脆性物质占有多大比例。全岩分析能确定矿物的类型,但是资料相对较少,且费用高。应用测井方法解释脆性物质含量时,应用多矿物最优化的方法[8],确定矿物骨架值是矿物含量精确解释否的关键。不同地区实际选取的矿物骨架参数与岩石的测井响应有关,与矿物自身骨架值相差较大,同时还受到测井曲线分辨率的影响,计算的矿物含量准确性相对较低,结果很难反映储层脆性物质的多少,解释的脆性指数准确性相对较低。在统计回归法中,首先选取敏感参数,再根据全岩分析确定的矿物含量建立统计模型。这种方法得到的脆性矿物含量受到曲线分辨率的限制,也很难得到准确的脆性矿物含量。

1.2 弹性参数法

弹性参数法应用岩石力学参数(弹性模量和泊松比)计算脆性指数[见式(3)]。弹性模量和泊松比并非直接反映岩石脆性的参数,但是弹性模量越大,泊松比越小,岩石脆性越好,通过对弹性模量和泊松比进行归一化,以此表示储层脆性。式(4)和式(5)分别为弹性模量和泊松比归一化计算公式。式(6)和式(7)为横、纵波时差计算弹性模量和泊松比的公式[9]。

(3)

IE=(E-Emin)/(Emax-Emin)×100%

(4)

Iμ=(μ-μmax)/(μmin-μmax)×100%

(5)

(6)

(7)

式中,IB为岩石脆性指数,%;IE为弹性模量计算脆性指数,%;Iμ为泊松比计算脆性指数,%;E为弹性模量,MPa;μ为泊松比,无量纲;Δts为横波时差,μs/ft(1)非法定计量单位,1 ft=12 in=0.304 8 m,下同;Δtc为纵波时差,μs/ft;DEN为岩石密度,g/cm3。

从式(3)～式(7)可知,岩石密度、横波和纵波时差确定后,即可计算泊松比和弹性模量,也就得到了储层的脆性指数。该方法简单,但是准确计算脆性指数的关键有2点:①泊松比和弹性模量的最大值和最小值的刻度;②横波测井费用高,不是所有井都能测偶极子横波,因此,需要进行横波时差曲线重构,构建的方法和模型的精度直接影响脆性解释的精度。

综合以上分析表明,弹性参数法适用范围更广,脆性指数解释的关键是横波时差曲线的重构、泊松比和弹性模量最大值、最小值的选取。结合徐家围子地区沙河子组的岩性特征,储层脆性指数解释方法选择弹性参数法。

2 脆性指数变化的规律

2.1 脆性指数变化分析

从矿物模型法可知,当岩石中脆性矿物含量发生变化时,脆性指数大小必将随脆性矿物含量增加而增加,随脆性矿物的减少而减少,但当岩石的分选、胶结类型和粒度等发生变化时,脆性指数的大小变化也是脆性指数研究的内容。

从式(3)～式(7)可知,应用弹性模量和泊松比能计算脆性指数。从式(3)可知,脆性指数是脆性弹性模量和脆性泊松比之和除以2,因此,可以选择弹性模量或泊松比研究脆性指数变化的规律。随着岩石结构特征变化,测井测得的横波和纵波速度必然发生变化,那么泊松比或弹性模量计算的脆性也必然发生变化。由式(5)得到泊松比与横纵波时差比值的关系式(8),再分析脆性指数与横纵波时差比值的关系式,即应用泊松比研究脆性指数随岩石物理特征变化时的变化规律

(8)

假设块状地层、各向均质条件下,进行理论计算,泊松比最小值取石英的泊松比(0.135),最大值为纯泥岩的泊松比(0.308),建立脆性指数、泊松比与横纵波时差比值的关系(见图1)。

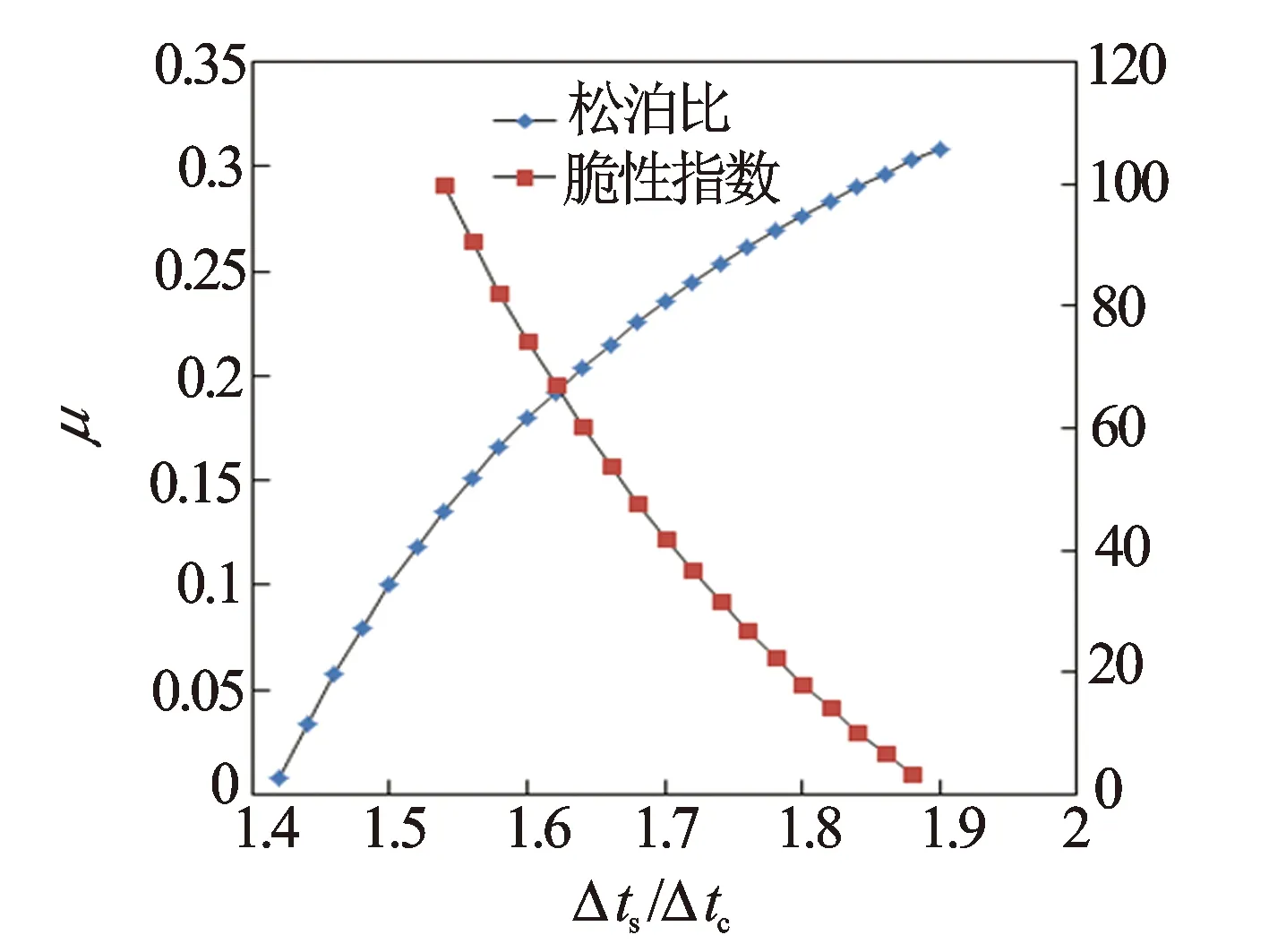
图1 脆性指数、泊松比与横纵波时差的比值关系图

2.2 脆性指数变化规律

根据图1可知,当岩石的横纵波时差比值变大时储层脆性变差,当岩石的横纵波时差比值变小时储层脆性变好,可知储层岩石分选性与物性变化、胶结程度变化时脆性变化的规律。对于岩石分选性,分选越好,泥质含量越低,导致横纵波时差比值越小,脆性指数越大;分选越差,泥质含量越高,脆性指数越小。对于物性,孔隙度越大,横纵波时差比值越小,脆性越大;孔隙度越小,横纵波时差比值越大,脆性越小。对于胶结物类型:常有钙质胶结物、硅质胶结物、铁质胶结物和泥质胶结物这几种类型,对应的横纵波时差比值一般是钙质的最小、泥质的最大,因此,脆性指数是钙质胶结最大,泥质胶结最小。对于薄互层组合,砂岩岩石结构由块状演变成薄互层或有层理界面,横纵波时差增大,岩石脆性指数变小。

据此,还可以对脆性解释的合理性进行判别。对于没有进行岩石脆性实验的地区,缺乏实验资料对解释结果的验证,无法确定解释结果的合理性时,可以根据横纵波时差的变化范围,确定合理的脆性指数变化范围。

3 徐深气田沙河子组岩石脆性指数解释方法

3.1 横波时差重构模型

横波时差曲线的重构方法较多,有理论模型法和经验公式法(统计回归法)2类。其中理论模型法包括Greenberg-Castagna模型、Xu-White模型、Biot-Gassman模型、Cemented模型、Krief模型等[10]。这些模型中需要确定的参数较多,且无法验证参数的准确性,同时考虑到模型的实用性,因此,采用统计回归的方法来建立横波时差解释模型。

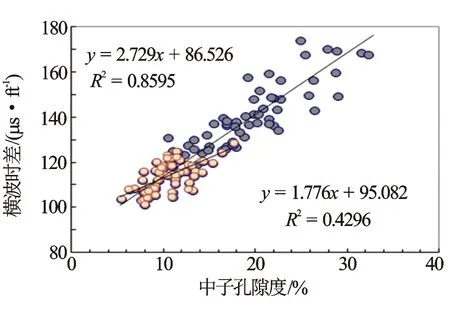
图2 实测横波时差与中子孔隙度关系图(分岩性)

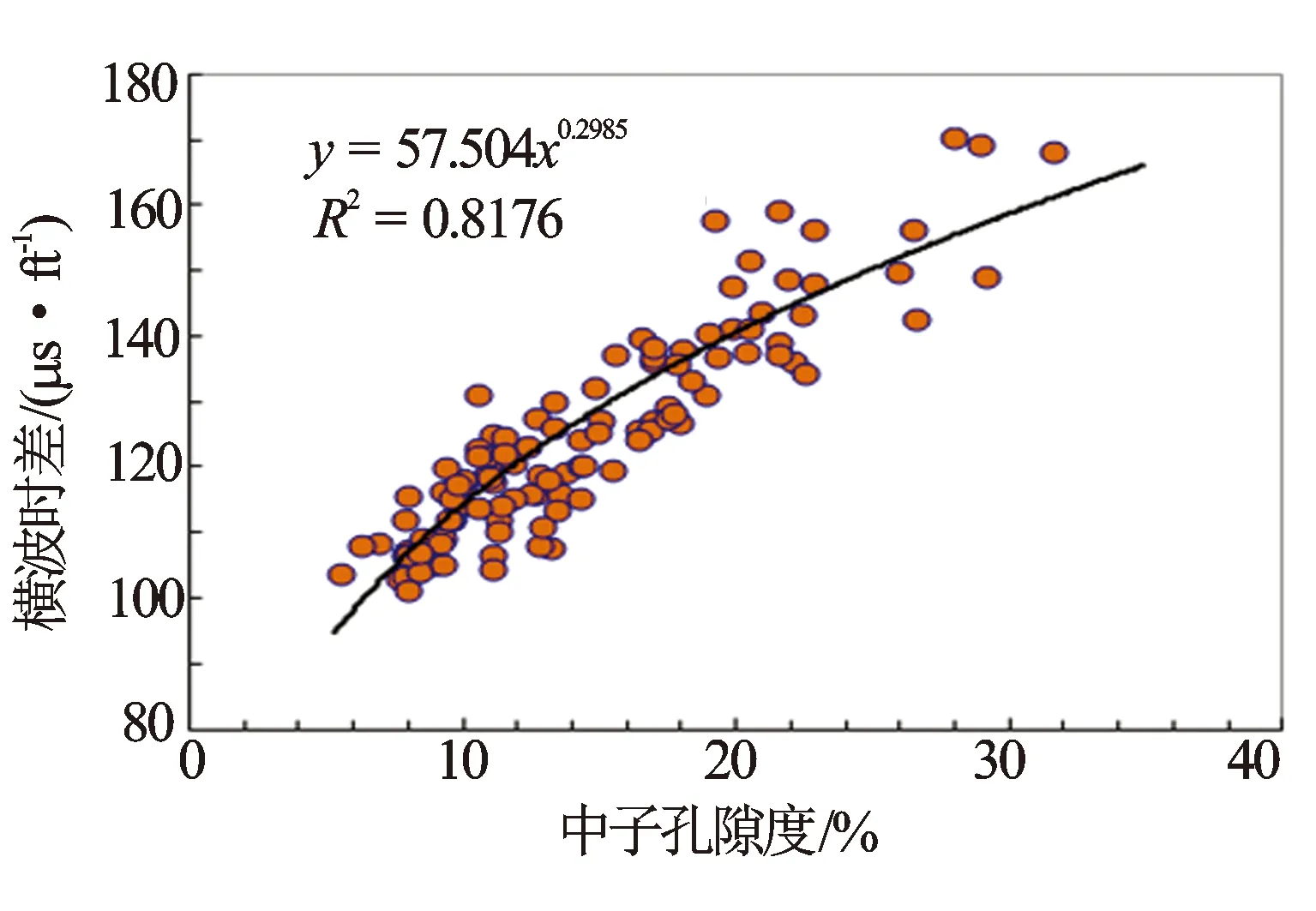
图3 实测横波时差与中子孔隙度关系图(不分岩性)

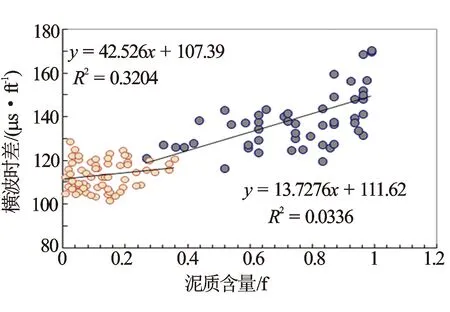
图4 实测横波时差与泥质含量关系图(分岩性)

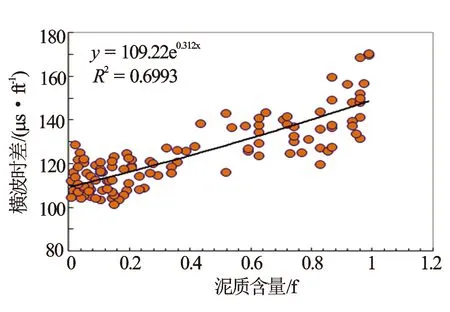
图5 实测横波时差与泥质含量关系图(不分岩性)

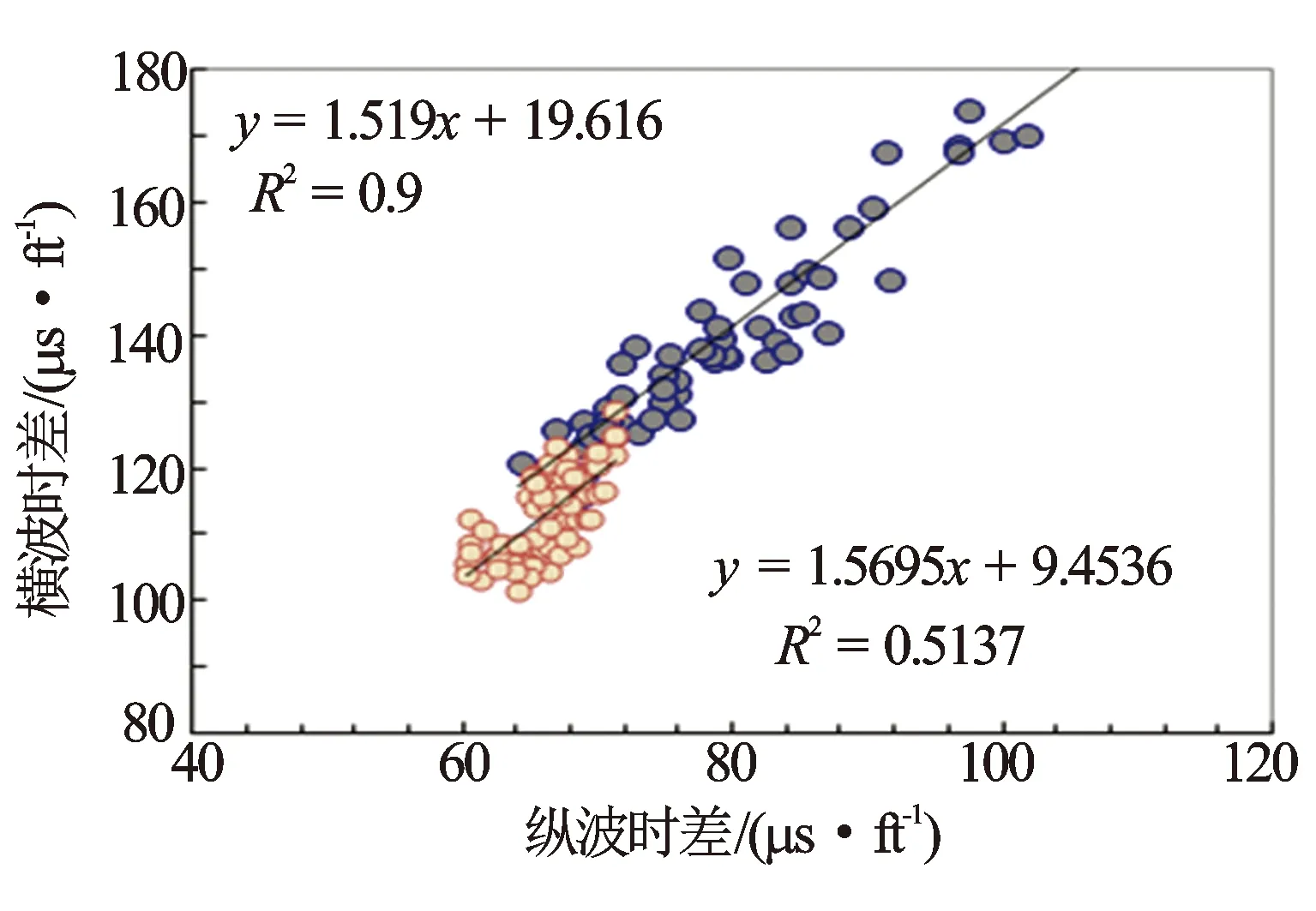
图6 实测横波时差与纵波时差关系图(分岩性)

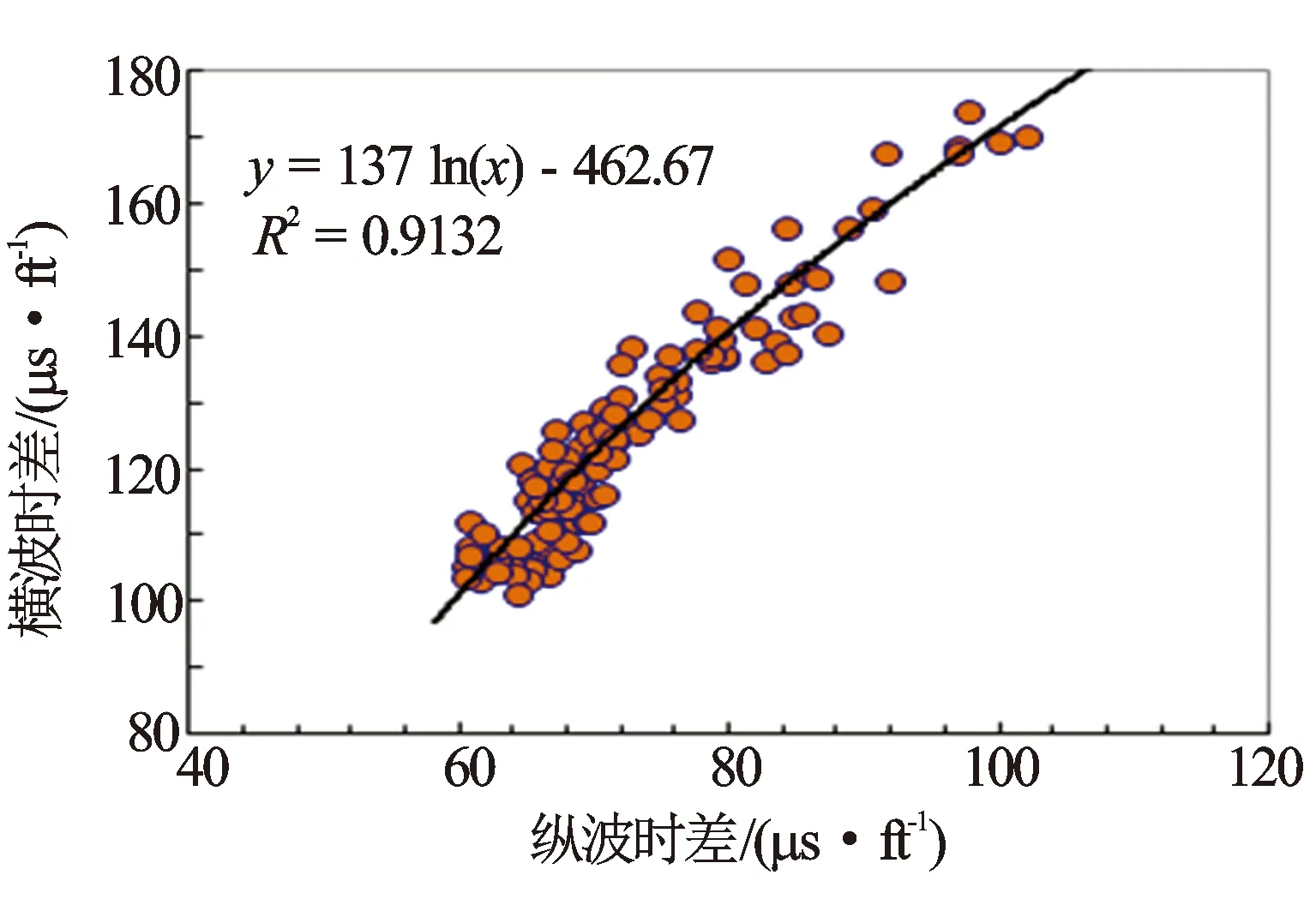
图7 实测横波时差与纵波时差关系图(不分岩性)

岩石的脆性反映岩石力学特征,选择敏感参数重构横波时差曲线时,应选择反映岩石结构特征的信息。图2、图4、图6、图8、图9分别为横波时差与中子孔隙度、自然伽马相对值(ΔGR)、纵波时差、岩性密度和深侧向电阻率之间的关系图。中子孔隙度、自然伽马相对值、纵波时差与横波时差的相关系较好,为敏感参数,岩性密度和深侧向电阻率不敏感。图2可见,砂岩和泥岩具有较好的线性关系。图3横波时差与中子孔隙度整体具有幂指数关系。图4可见,砂岩和泥岩均不具有较好的线性关系。图5可见,当岩性从砂岩向泥岩变化时,整体具有指数关系。图6中砂岩和泥岩具有较好的线性关系。由图7可见,当岩性从砂岩向泥岩变化时,整体具有对数关系。因此,选用中子孔隙度、ΔGR及纵波时差建立横波时差重构模型。结合地区流体性质,分别建立含有中子项的公式(8)和不含有中子项的公式(9)。

35.98e(0.308Vsh)-152.61R=0.85

(8)

Δts,cg=68.28ln (Δtc)+53.97e(0.308ΔGR)-

228.92R=0.85

(9)

式中,Δts,cg为重构的横波曲线,μs/ft;φN为中子孔隙度,%;Δtc为纵波时差,μs/ft;Vsh为泥质含量。

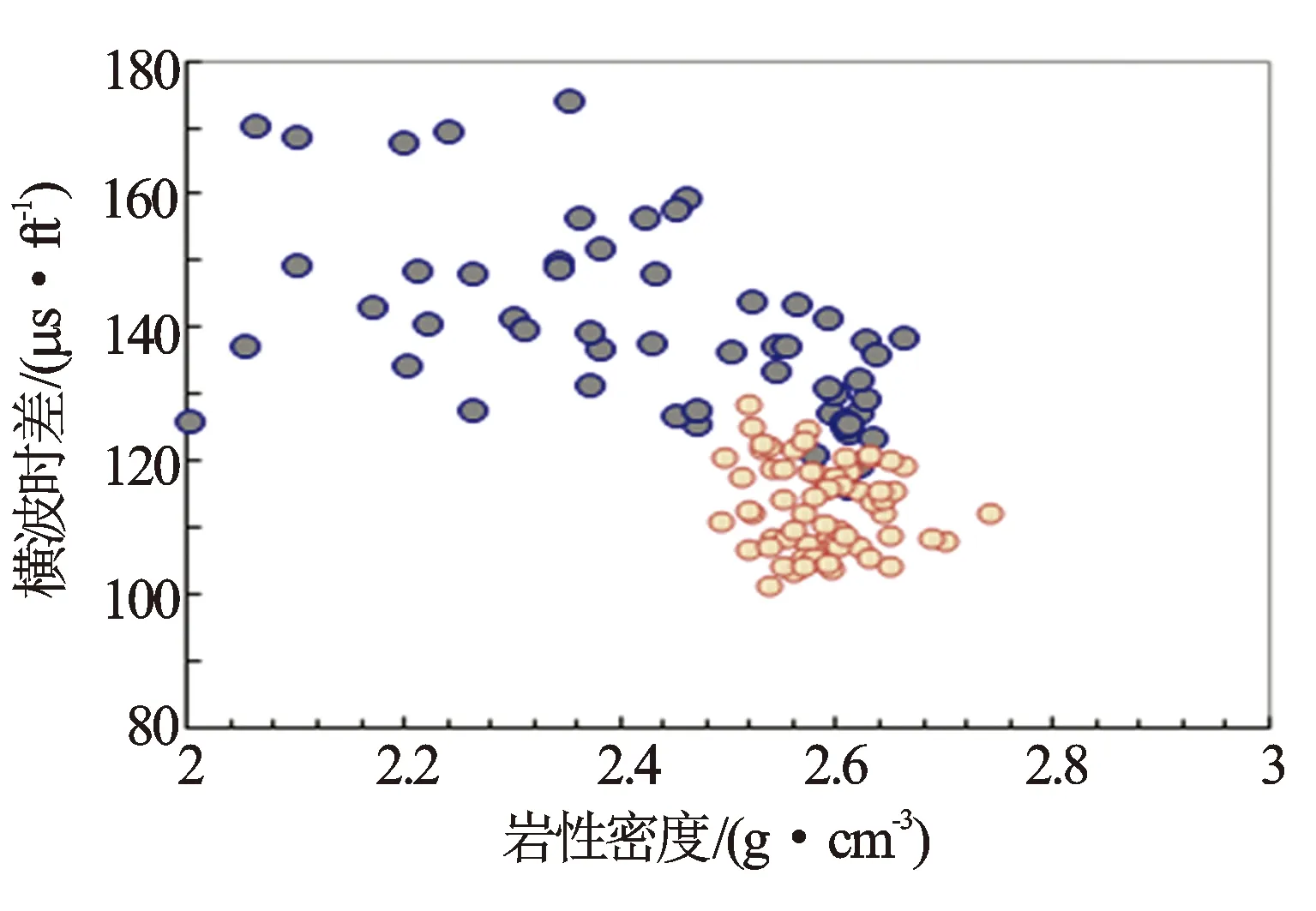
图8 实测横波时差与岩性密度关系图(分岩性)

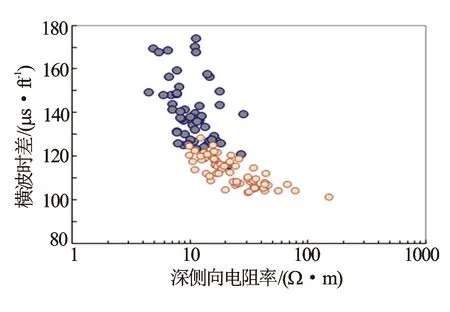
图9 实测横波时差与深侧向电阻率关系图(分岩性)

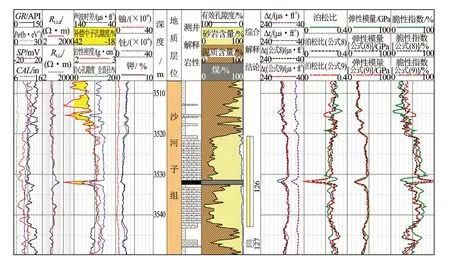
图10 达深×井不同横波模型解释结果对比图

分别应用式(8)和式(9)计算横波时差,并以此计算泊松比、弹性模量和脆性指数,对比实测的横波时差及相关参数(见图10)。3 510.0～3 548.0 m进段岩性包括砂岩、砂砾岩、泥岩和煤,重构的横波时差在各种岩性段与测井值相差小于3 μs/ft,泥岩段用式(8)计算的结果横波时差更接近测井实测值,计算的泊松比、弹性模量和脆性指数也是如此;砂岩段和砂砾岩段,横波时差及相关参数相差不大;煤层段横波时差及相关参数相差较大。深度3 522.7～3 528.0 m,密度小于2.6 g/cm3为储层段,式(8)与式(9)计算的横波时差略有差异,相应的泊松比、弹性模量和脆性指数,式(9)计算的结果更接近实测横波时差测井的计算值。对比表明,由于天然气的挖掘效应,式(9)适用,能反映岩石力学性质的变化,解释的泊松比与实测曲线解释结果符合好;对于不含气储层,式(8)更适用。

3.2 脆性解释

3.2.1弹性模量和泊松比取值的意义

矿物组分法计算脆性的公式(1)表示的是脆性矿物在岩石矿物中所占有的含量,而弹性参数法计算脆性的公式(3)则是泊松比和弹性模量归一化后求和的平均值。研究根据其中一种边界(全是石英砂岩或泥岩),对这2种方法的内涵进行分析。

假设岩石全是石英砂岩,矿物组分法计算脆性的公式(1)可知,石英是脆性物质,当岩石全由石英组成,岩石的脆性指数为100%。同样的石英砂岩,弹性参数法计算脆性的公式(3)可知,泊松比和弹性模量的归一化值均为100%。此时泊松比归一化方程中,泊松比的最小值为石英的泊松比,最大值为研究区泥岩实际值;此时弹性模量归一化方程中,弹性模量的最大值取石英的弹性模量,最小值取研究区泥岩实际值。当岩石矿物发生变化时,脆性变差,对于矿物组分法而言是石英含量的减小,对于弹性参数法而言,则是计算的泊松比和弹性模量的变化,那么,两者的实际关系为随着石英含量减小,对应的泊松比和弹性模量的变化。因此,泊松比的最小值取石英的泊松比,最大值为研究区纯泥岩的泊松比,弹性模量的最大值为石英的弹性模量,最小值为研究区泥岩的弹性模量。在同类岩性中,以此取值,采用弹性参数法计算脆性指数具有可比性,否则只是某个区域的相对值。

3.2.2脆性指数解释及分析

徐家围子地区沙河子组岩石脆性计算时,按3.2.1中的分析结果进行取值,解释的脆性范围为46.7%～82.2%。该区没有进行岩石脆性实验,无法对解释结果的进行验证。而图1表示了脆性指数与横纵波时差比值之间的理论关系,研究区的横纵波时差比值范围在1.6～1.9,其中砂砾岩范围为1.6～1.7,确定储层脆性解释的范围为42.1%～74.3%。计算结果与理论分析结果的范围一致,中值一致,表明弹性参数法计算脆性指数反映了脆性矿物的含量。