旋转短基线北斗双天线/MIMU定向方法
2020-01-07蔡体菁高帅鹏赵梓超
刘 莹,蔡体菁,刘 洋,高帅鹏,赵梓超
(东南大学 仪器科学与工程学院,南京 210096)
利用北斗导航卫星确定运载体姿态,其优点是无累计误差、无需对准、精度高。如果把北斗导航卫星与微惯性测量单元结合,那么组合系统就可以连续地输出运载体的位置、速度、姿态角和航向角。目前商用的GPS两天线/MIMU组合系统都采用求解GPS整周模糊度的方法来确定组合系统的航向角[1-5]。当GPS导航卫星信号失锁,或载波相位发生周跳时,采用上述方法定向就要花费较长的时间。通过旋转天线的方式,不用求解全球导航卫星的整周模糊度,就可以得到航向角。
最近,俄罗斯中央电器仪表所Emelyantsev等人[6-8]提出了GNSS罗盘。该罗盘主要由GPS、GLONASS双天线接收机、MEMS传感器和旋转机构组成,GNSS天线基线长度小于载波相位的波长,静态试验结果显示该罗盘的航向误差为1°左右。2016年东南大学开始对旋转北斗短基线双天线定向开展研究,提出了北斗双天线基线连续旋转整周和 0~180°两位置的两种快速定向方法[9],试验表明,对于0.3 m的北斗短基线双天线,用上述方法得到的航向误差小于1°,与商业OEM定向板卡相比,上述方法定向速度快,定向精度高。
本文针对旋转短基线北斗双天线/MIMU组合系统开展定向研究,给出旋转MIMU定向算法、北斗双天线/MIMU组合系统扩展卡尔曼滤波状态方程,观测方程,以及组合系统的定向解算步骤,并给出旋转短基线北斗双天线/MIMU组合系统室外动态和船载试验结果,以及双天线基线长度变化试验结果。
1 系统硬件
针对旋转短基线北斗双天线/MIMU组合系统定向原理和方法,东南大学研制出了实验室样机,见图1。该系统的硬件主要由旋转机构、北斗双天线、MIMU、导航计算机等组成,如图2所示。旋转机构采用的是力矩电机,旋转机构转过的角度用光电编码器记录,北斗双天线接收机板卡为OEM617D,MIMU是STIM300,导航计算机由DSP和FPGA芯片组成,芯片采用的是TMS320C6748和EP3C25U256I7。

图1 旋转北斗双天线/MIMU组合系统实物Fig.1 Rotating short-baseline BDS dualantenna/MIMU integrated system
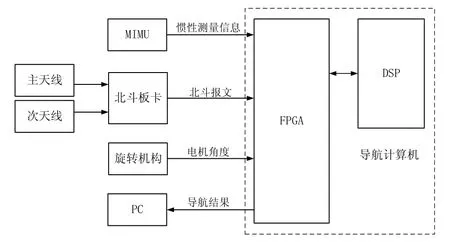
图2 旋转北斗双天线/MIMU组合系统构成Fig.2 Composition of the integrated system
2 定向方法
旋转短基线北斗双天线/MIMU组合系统定向方法是:通过旋转捷联惯导定向算法求出载体航向角的递推值;然后利用北斗双天线的位置、速度和载波相位信息作为组合系统的外观测量,根据组合系统的扩展卡尔曼滤波方程,估计出载体的航向角误差;最后经误差补偿修正得到载体的真实航向。
2.1 旋转MIMU定位定向算法
MIMU被放置在旋转机构上,MIMU的z轴与旋转机构的旋转轴重合,MIMU随旋转机构绕旋转轴转动。旋转机构与载体固联,MIMU坐标系b与载体坐标系o的转换矩阵Cob为:

其中,θ=ωct+θ0为旋转机构转过的角度,θ0为初始角度,ωc为旋转机构旋转角速度。
采用四元数q解算MIMU的姿态,姿态方程为:

其中:
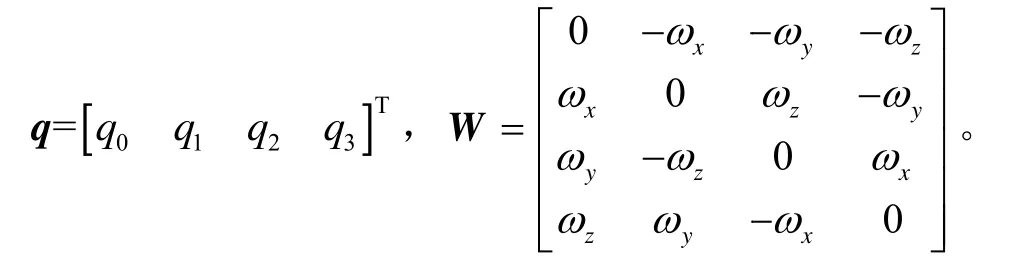
假设地理坐标系n与MIMU坐标系bb的转换矩阵为,那么四元数q与姿态矩阵的关系为:
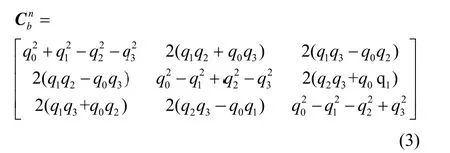
地理坐标系n与载体坐标系o的转换矩阵为:
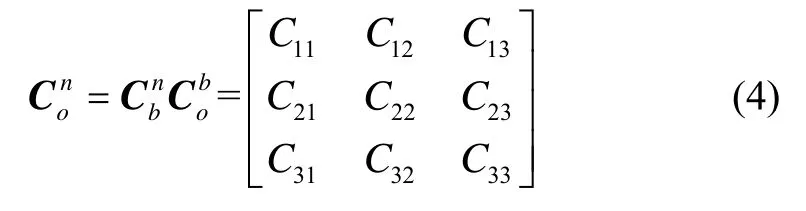
载体的航向角、俯仰角、横滚角分别为:
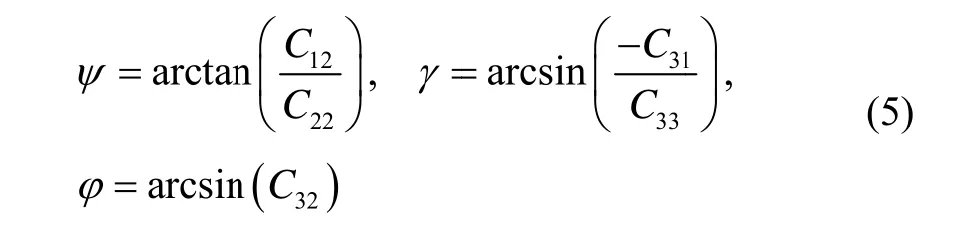
与MIMU坐标系b固联的捷联导航方程为:
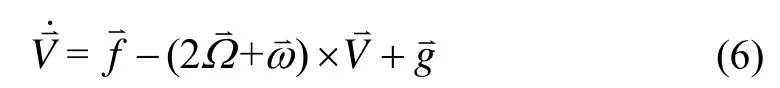
对式(6)积分,除去有害加速度,就得到k时刻对地速度,在此基础上进一步积分,就得到载体的位置。经纬度表达式如式(7)所示:
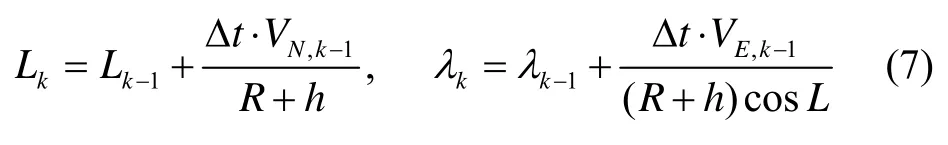
其中,R为地球曲率半径,h为椭球高,分别表示载体k时刻的经度和纬度,分别为载体k时刻的东向和北向速度。
2.2 组合系统状态方程
旋转北斗双天线/MIMU组合系统扩展卡尔曼滤波状态方程为:
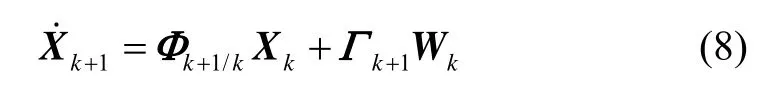
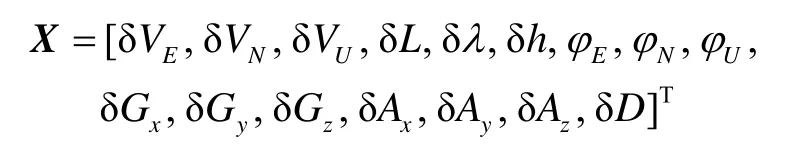
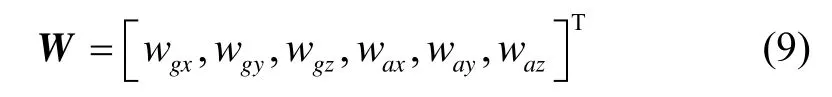
状态转移矩阵:
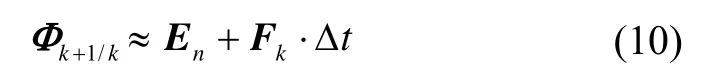
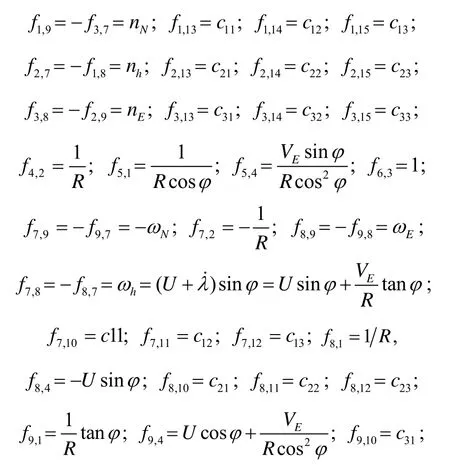
2.3 组合系统观测方程
北斗双天线载波相位双差数学模型为[9]:
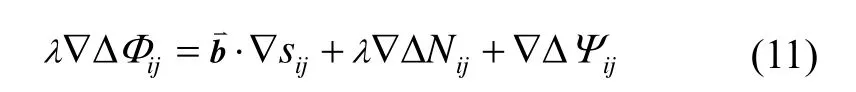
其中,λ是北斗卫星波长,∇ΔΦij是北斗双天线载波相位双差值,是双天线基线向量,∇sij是2颗北斗卫星到天线的单位向量双差,∇ΔNij是北斗双天线载波相位双差的整周模糊度,∇ΔΨij是北斗双天线载波相位测量偏差的双差值。
旋转北斗双天线/MIMU组合系统的卫星载波相位双差观测量为
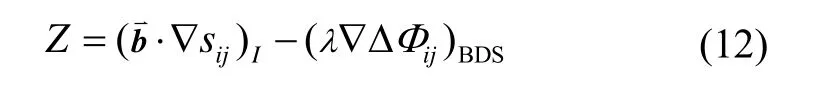
把式(11)代入式(12),得:
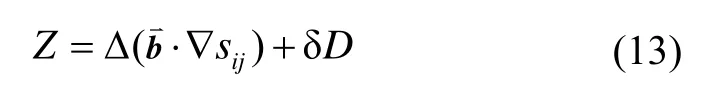
在导航坐标系n中,捷联惯导系统计算的姿态角与真实姿态角存在一个误差角。对式(13)进行线性化处理,忽略高阶量,有下式:
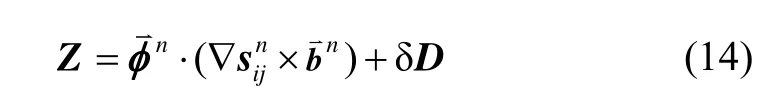
旋转北斗双天线/MIMU组合系统观测方程为
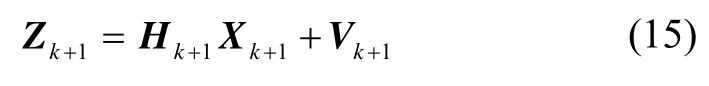
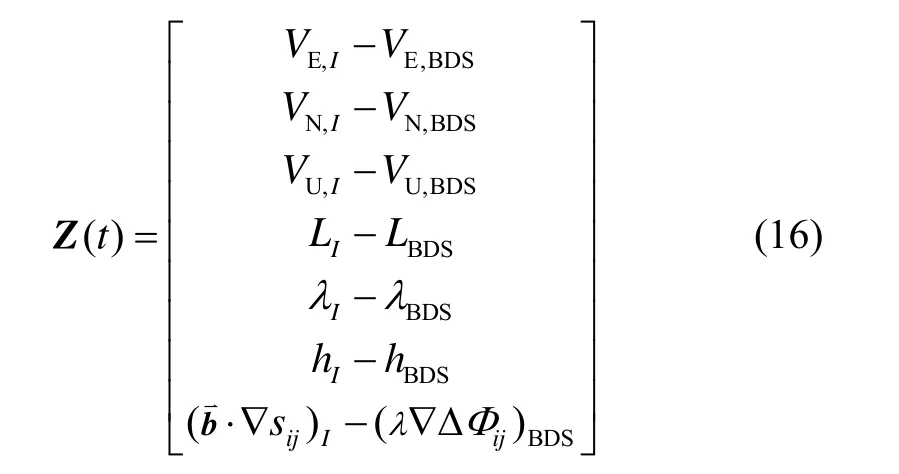
其中:VE,I、VN,I、和VU,I分别是旋转捷联惯导计算得到的东向、北向和天向速度;VE,BDS、VN,BDS、VU,BDS是北斗双天线输出的东向、北向和天向速度;LI、λI、hI分别是旋转捷联惯导计算得到的经度、纬度、高度;LBDS、λBDS、hBDS分别是北斗双天线输出的经度、纬度、高度。
观测矩阵Hk+1= [hi,j](i= 1,⋅⋅⋅,7 ;j= 1,⋅⋅⋅,16)中的非零项为:
3 组合系统定向计算步骤
旋转北斗双天线/MIMU组合系统定向算法流程如图3所示。MIMU陀螺仪输出经误差补偿后用式(2)和式(3)计算得到,通过式(4)和式(5)得到航向角、俯仰角、横滚角。MIMU加速度计输出经误差补偿和姿态矩阵变换得到,通过式(6)计算得到载体的位置和速度。扩展卡尔曼滤波器根据惯导信息和北斗双天线接收机提供的位置、速度、卫星星历、载波相位等信息,估计出误差状态量,经闭环反馈获得精确的导航参数,最后组合系统输出载体的航向角以及其他导航参数。
4 试验结果
4.1 变基线长度动态试验
把旋转北斗双天线//MIMU组合系统放置在东南大学中心楼楼顶露天阳台的一个小车上,如图4所示。实验轨迹如图5所示。楼顶周围无遮挡,它能够接收到良好的北斗信号。在试验过程中,将旋转北斗双天线/MIMU组合系统与高精度激光陀螺捷联惯性导航系统(参考系统)固联在一起,保持航向一致。双天线基线长度能够自由调节。
当双天线基线长度分别为10 cm、20 cm、30 cm时,旋转北斗双天线/MIMU组合系统与高精度激光陀螺捷联惯性导航系统的航向角误差、俯仰角误差和横滚角误差如图6~8所示,与参考系统相比组合系统的航向角、俯仰角和横滚角误差如表1所示。

图4 变基线长度动态试验Fig.4 Dynamic experime nt for different baseline length s
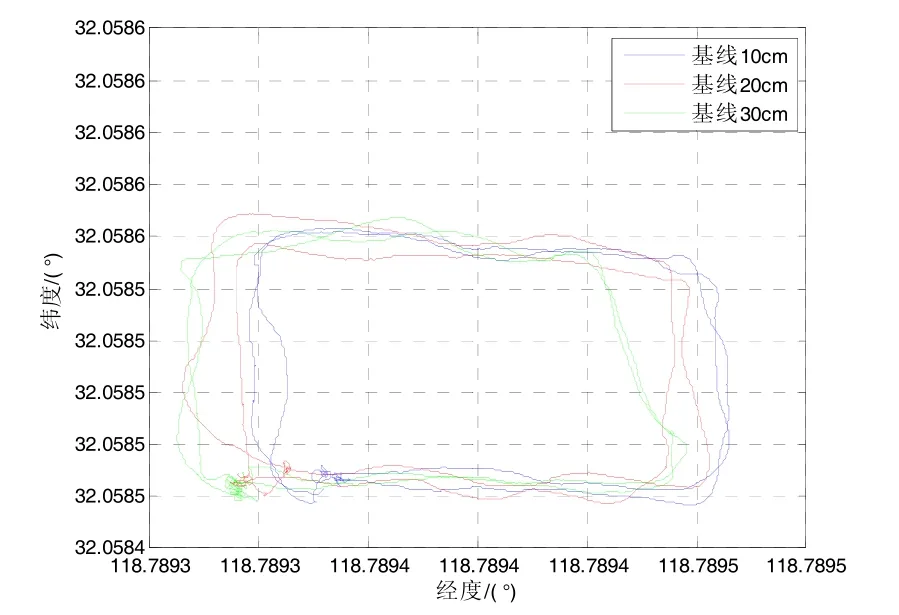
图5 变基线长度动态试验轨迹Fig.5 Dynamic experiment track for different baseline lengths
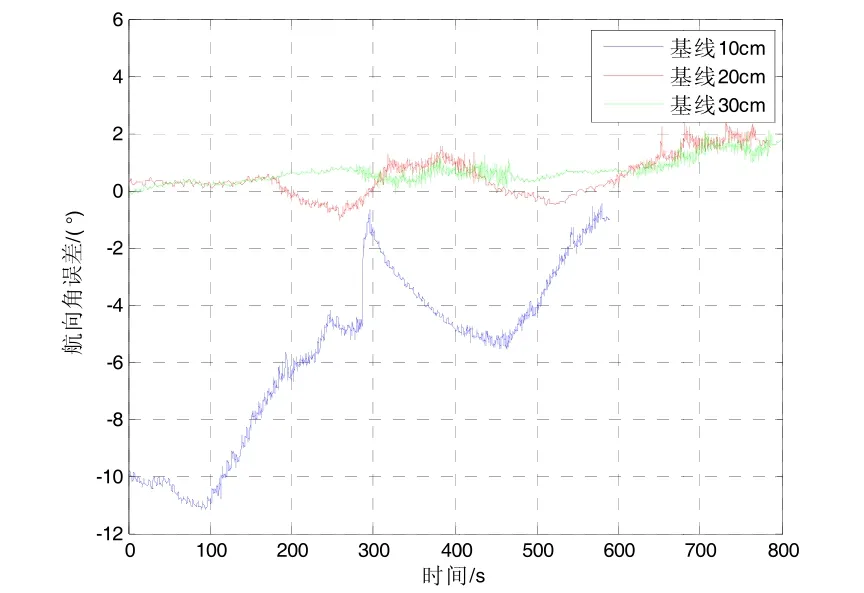
图6 双天线基线长度不同时的航向角误差变化曲线Fig.6 Headding error for diifferent baselinee lengths
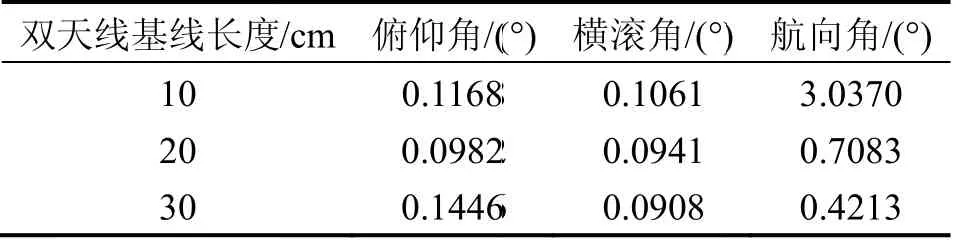
表1 姿态角误差(1σ)Tab.1 Attitude errors (1σ)
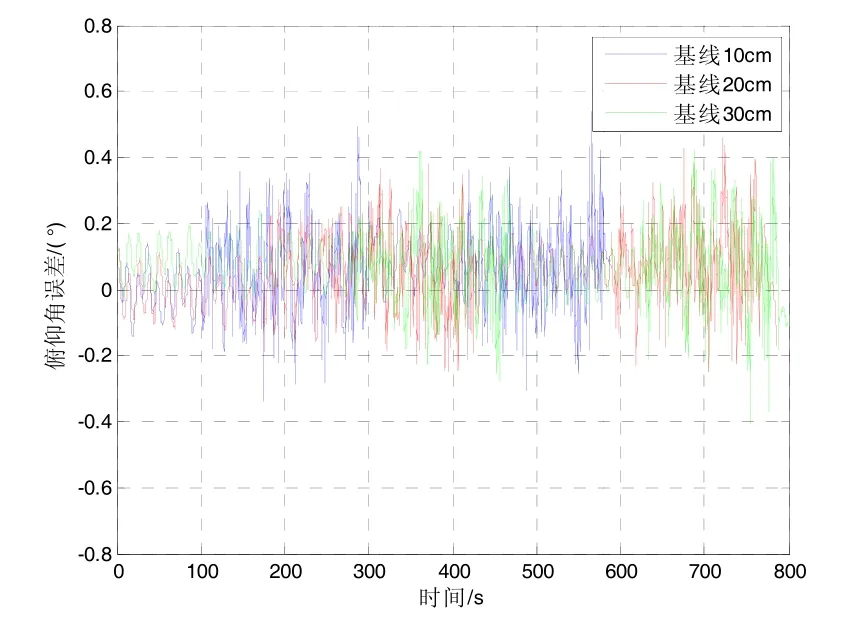
图7 双天线基线长度不同时的俯仰角误差变化曲线Fig.7 Pitch error for different baseline lengths
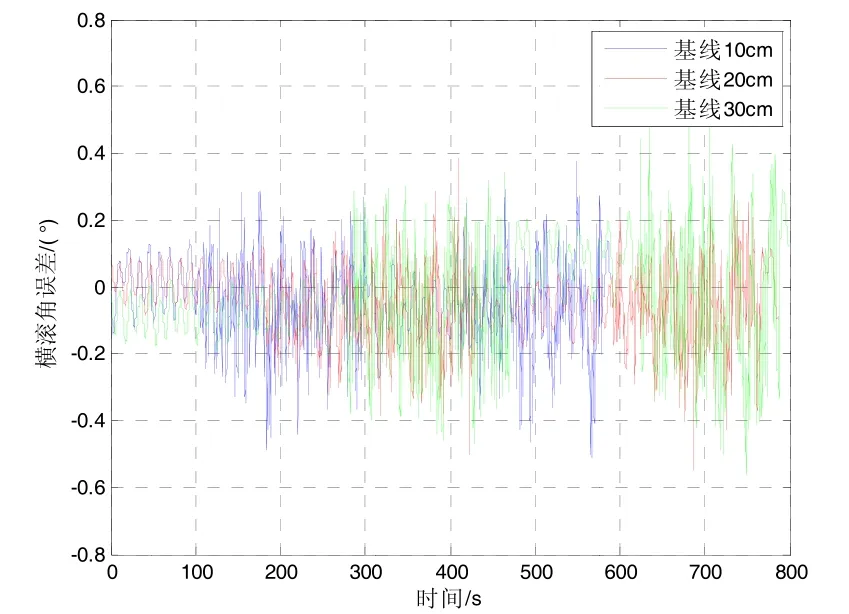
图8 双天线基线长度不同时的横滚角误差变化曲线Fig.8 Roll error forr different baseline lengths
4.2 船载试验
2018年10月旋转北斗双天线/MIMU组合系统在南京玄武湖上进行了船载试验。该组合系统与GPS/激光捷联组合导航系统通过同一个过渡板固定在船的甲板上,两组合系统的导航坐标系保持一个固定值,试验轨迹如图9所示,试验装置如图10所示。北斗双天线基线长度为0.3 m。经与GPS/激光捷联组合导航系统比较,旋转北斗双天线/MIMU组合系统的航向角误差、俯仰角误差、横滚角误差分别为0.72°、0.12°、0.11°(1σ)。
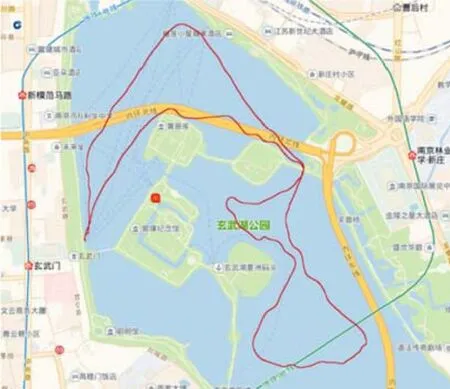
图9 旋转北斗双天线/MIMU组合系统船载试验轨迹Fig.9 Ship experimenttrack of the integrated system

图10 旋转北斗双天线/MIMU组合系统船载试验Fig.10 Ship experiment of the integrated system
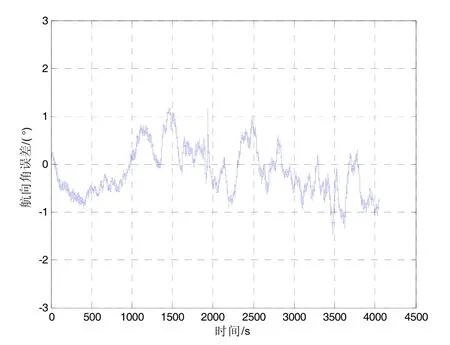
图11 旋转北斗双天线/MIMU组合系统航向角误差Fig.11 Heading error of the integratedsystem
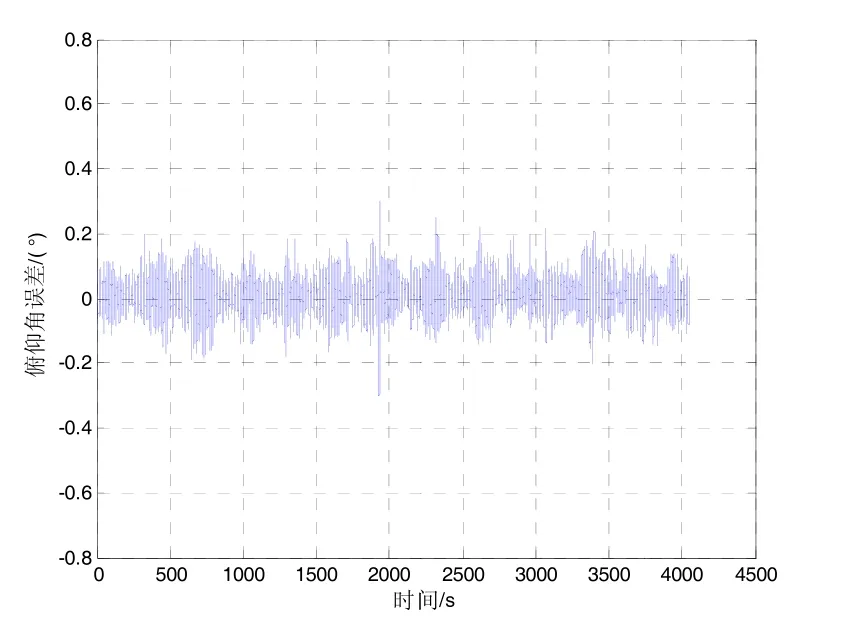
图12 旋转北斗双天线/MIMU组合系统俯仰角误差Fig.12 Pitch error of the integrated system
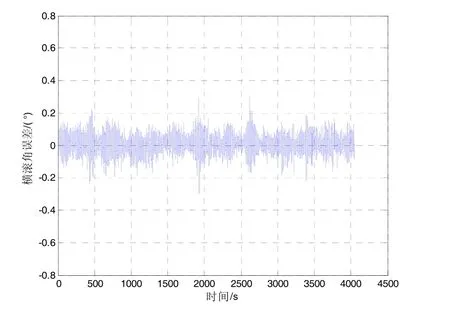
图13 旋转北斗双天线/MIMU组合系统横滚角误差Fig.13 Roll error of the integrated system
5 结 论
短基线北斗双天线/MIMU组合系统由北斗卫星定位系统和基于MIMU的捷联惯导系统组成,它以北斗天线的速度、位置和北斗卫星信息作为卡尔曼滤波器的观测量,经数据融合后给出组合系统的航向角和姿态角。该组合通过旋转天线的方式,代替了求解全球导航卫星的整周模糊度,得到航向角。
短基线北斗双天线/MIMU组合系统室外动态和船载试验表明,当基线长度为0.3 m时,水平姿态角误差小于0.2°,航向角误差小于1°。本组合系统可广泛应用于无人艇和无人机领域。
