基于模式判别的运动学约束辅助空中动基座对准方法

赵 宾，曾庆化，刘建业，高春雷

（1.南京航空航天大学 自动化学院 导航研究中心，南京 210016；2.南京航空航天大学金城学院，南京 211156）

对于采用北斗/SINS组合导航的运载体，如果能充分利用组合导航系统中北斗卫星导航系统的信息对捷联惯导系统（Strapdown Inertial Navigation System,SINS）进行初始化，则可以减小系统对载体的依赖，实现自主对准。由于载体任务、环境的不同，往往需要在不同的机动下完成初始对准：在低机动情况下，收敛速度较快，但是方位失准角可观测度较低[1]，导致方位失准角的对准精度较低；在高机动情况下，方位失准角可观测性得到提高，但机动运动同时也会增强系统的非线性，对卡尔曼滤波器的估计效果产生一定的负面影响，对准的快速性和精度受到影响[2]。且在实际战场中，北斗信号很容易受到干扰，无法保证其信息的有效性。如何综合提高载机各种机动情况下的对准性能，是亟需解决的问题。

模型辅助导航是一种低成本的 SINS误差修正方法[3]，主要有动力学辅助和运动学约束两种模式。由于飞机等空中运载体具有大量子系统和强非线性特性，所以建立简洁实用的动力学模型比较困难。相对来讲，运动学约束是SINS误差控制的常用手段，它通过将飞行器的运动信息与现有的导航系统信息相融合，有效提高导航系统的导航精度与可靠性，无需增加额外的传感器，具有自主性强、成本低和零载重等优点。

当载体在地面上运动且没有侧滑时，载体侧向和垂向速度为 0，称之为速度约束。国内外学者对速度约束在地面各类载体中的应用进行了大量的研究[4-6]。此外，车载导航的其他运动约束也得到充分研究：文献[7]建立了适合于四轮车辆的转弯半径、前轮摆角、轴距的车辆运动学模型，来辅助车载导航。文献[8]在常规速度约束的基础上，建立了转弯过程中的速度约束，实现了卫星中断情况下的车辆定位。文献[9]论述了车辆速度约束以及加速度输出计算的姿态角约束方法，增强惯性导航系统的性能。文献[10]利用GPS输出的水平速度获得伪航向角作为约束信息，提高航向精度，但仅适用于无侧滑角的情况。文献[11]结合里程计测量信息构建完整速度约束，并提出构建虚拟位置观测信息的方法，以提高卫星中断期间的导航精度。综上可知：目前运动学约束辅助导航的研究多针对载体在地面运动的情况，空中载体的运动学约束尚未见到相关研究的报道。由于气流角的存在以及空中运动的特点，即使飞机稳态飞行过程中，上述速度约束、转弯约束、姿态角约束等条件也不再适用。

本文通过对飞机空中运动的状态进行分析，挖掘系统存在的合理约束，提出一种基于运动学约束辅助的捷联惯导系统空中动基座初始对准方法。在不增加辅助传感器的前提下，建立飞机角速度运动学模型，进行运动模式判别，构造虚拟量测方程辅助北斗卫星导航系统进行空中动基座对准。在载体低机动情况下提高动基座对准的精度，在载体高机动情况下提高动基座对准的快速性，满足各种机动情况下的机载捷联惯导系统空中对准精度、快速性等综合需求。

1 基于运动学约束辅助的空中动基座对准方案设计

因此，在空中动基座对准过程中，选择捷联惯导系统导航解算得到的速度和北斗卫星导航系统测量得到的速度的差值作为一组量测信息；再建立飞机角速度运动学模型，引入运动模式判别方案判断运动约束的可用性。在运动约束可用时，将捷联惯导系统解算的角速度与理想的角速度（近似为 0）的差值作为另一组量测信息。采用两者结合共同进行量测更新，用卡尔曼滤波器对捷联惯导系统的失准角进行估计和校准，完成飞机空中动基座对准。基于运动学约束辅助的机载捷联惯导系统空中动基座对准方案如图1所示。

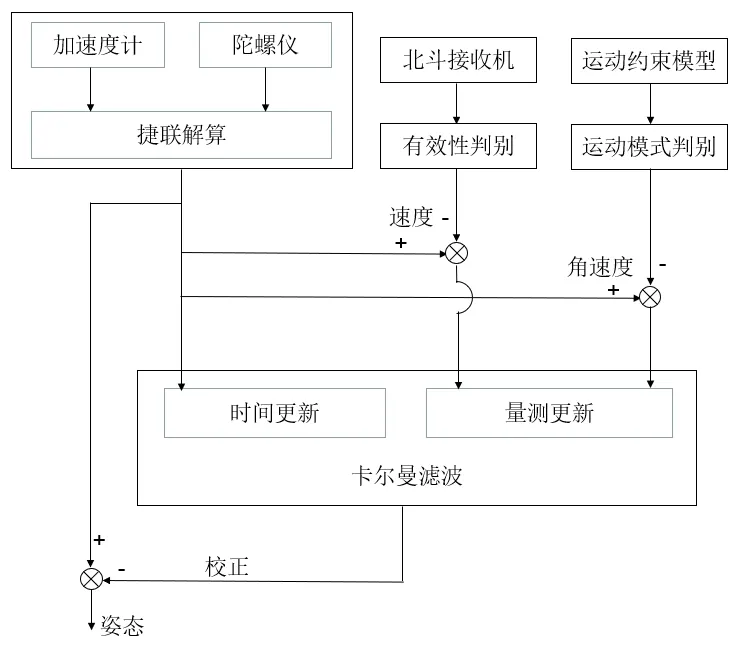
图1 基于运动学约束模型辅助的捷联惯导系统空中动基座对准方案框图Fig.1 In-flight moving-base alignment scheme of SINS based on kinematic constraint model

采用运动模式判别方案检测到飞机处于非角运动状态时，即引入角速度约束模型，联合北斗卫星导航系统信息进行量测更新。当检测到飞机处于角运动状态时，即对角速度约束辅助进行隔离，角速度虚拟量测信息不参与滤波器的量测更新，仅由北斗卫星导航系统进行量测更新。在应用中，能够比较方便地根据可用信息切换组合模式。该方案可以在不增加额外传感器的前提下，综合提高北斗卫星导航系统辅助捷联惯导系统动基座对准的精度和快速性。

由上述方案设计可知，角速度运动约束模型和角运动模式判别是实现本方案的关键环节，因此首先对角速度运动学约束模型构建和角运动模式判别方案进行研究。

2 飞机角速度运动学约束模型构建

导航坐标系选取东北天地理坐标系，飞机机体坐标系选取右前上坐标系。在捷联惯导系统中，角速度表达式如下：

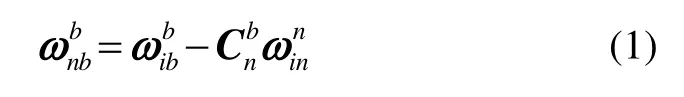
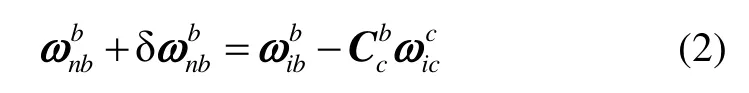
c系和n系之间存在计算误差，因此代入式(2)：

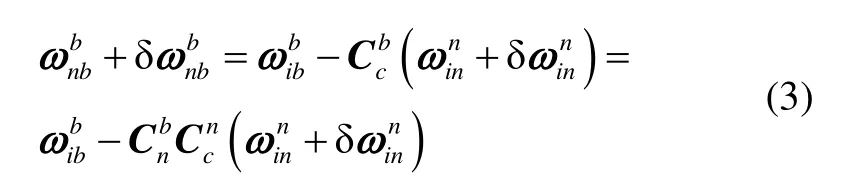
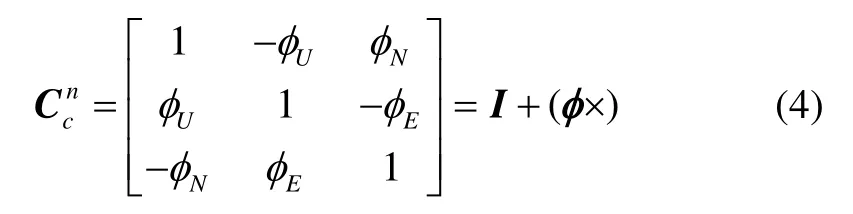
式(3)可展开为：

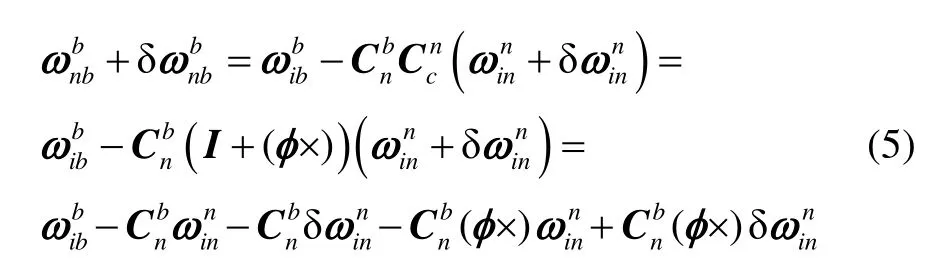
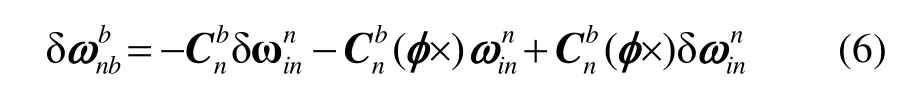
忽略二阶小量可得：

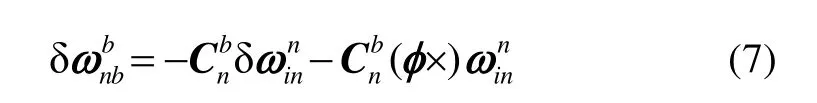
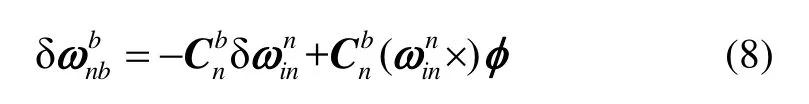
由第1节的分析可知：当载体处于非角运动状态时，地球自转和载体在地球表面运动所产生的角速度分量量级较小，可认为机体坐标系相对于导航坐标系的角速度近似为零；而捷联惯导系统导航解算得到的角速度实际值，由于误差 的存在并不为零。因此，可将机载捷联惯导系统解算得到的角速度实际值在机体坐标系、、轴上投影作为动基座对准的虚拟量测信息，并将地球自转和载体在地球表面运动所产生的角速度分量视为量测信息的噪声信息进行处理。

则可通过式(8)构建运动约束虚拟量测方程，如式(9)所示。

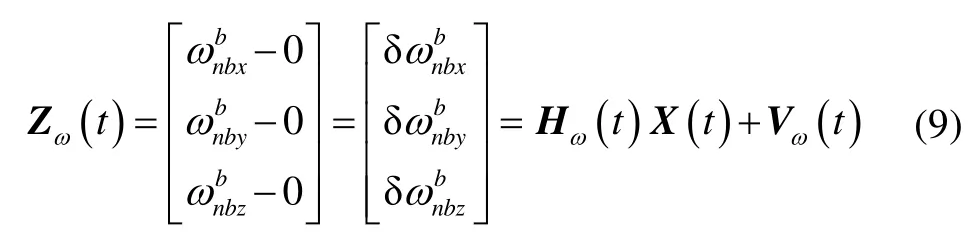
3 基于残差的角运动模式判别方案

在飞机空中运动过程中，对其角运动模式进行实时的判别，正确控制角速度约束的使用，是本算法应用的关键。对运动学约束辅助的空中动基座对准算法进一步分析可知，式(9)中虚拟量测信息是由捷联惯导系统解算的角速度构成，即角速度值将通过量测信息对滤波器产生影响。从这个角度出发，考虑将系统级故障检测的思路用于运动约束辅助对准滤波器中，实时检测虚拟量测信息的有效性。

该设计思想如下：将系统处于角运动的状态视为非稳态（类比于故障检测中的故障状态），将系统处于非角运动的状态视为稳态（类比于故障检测中的非故障状态），通过残差检验法实时判断系统是否存在稳态。若检测到有“故障”，则表明系统处于角运动状态（非稳态），机体坐标系相对于导航坐标系的角速度理想值不再为0。显然，由载体角运动引起的“故障”将直接造成虚拟量测信息无法表征实际的运动角速度信息，则角速度虚拟量测信息不参与滤波器的量测更新，仅由北斗卫星导航系统进行量测更新。反之，若检测到“无故障”，则表明系统处于非角运动状态（稳态），引入角速度约束模型，联合北斗卫星导航系统信息进行量测更新。

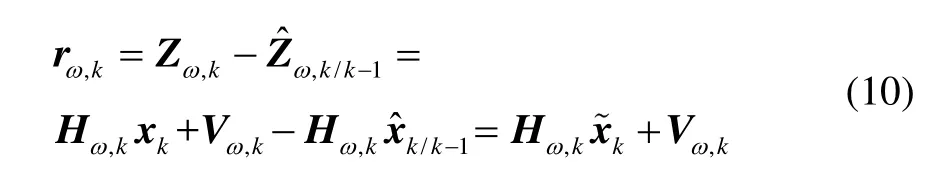
飞机角运动带来的实际角速度将通过量测残差向量对滤波器产生很大影响，甚至导致滤波发散。

其方差为：

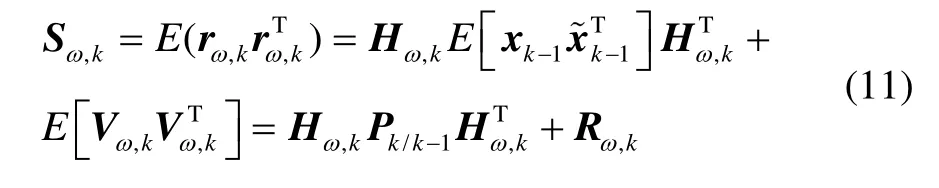
当飞机处于非角运动状态时，残差rω,k较小；当飞机处于角运动状态时，残差rω,k急剧增大。因此，通过对残差rω,k进行检验即可判别飞机的角运动状态，从而确定运动约束是否可用。构建角运动模式检测函数：

选择适当的阈值TD，当λω,k＜TD时，则判定飞机处于非角运动状态，运动约束有效。

需要特别指出的是：由于本方法中将地球自转和载体在地球表面运动所产生的角速度分量视为量测信息的噪声信息进行处理，所以非角运动状态时量测向量的残差均值并不为0，λω,k也不服从χ2分布，TD无法按照误警率计算得到。在实际应用中，需对飞机的角速度数据进行预分析，综合考虑所选用惯性器件精度、振动环境等多种因素影响，确定TD取值。

4 基于运动学约束模型辅助的空中动基座对准误差模型

4.1 对准系统状态方程

选取捷联惯导系统的数学平台误差角φE、φN、φU，速度误差δvE、 δvN、 δvU，陀螺随机常值漂移εbx、εby、εbz，陀螺一阶马尔可夫过程εrx、εry、εrz，加速度计一阶马尔可夫过程 ∇x、 ∇y、 ∇z为对准滤波的状态量：

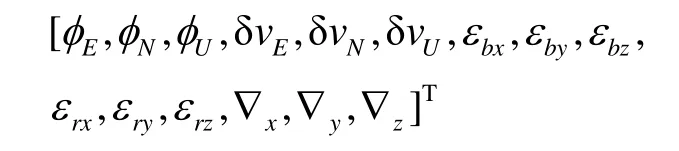
则状态方程为：

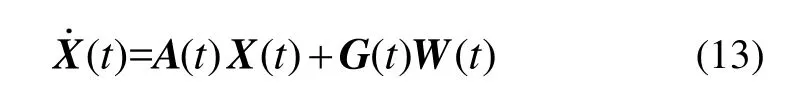
式中，X(t)为状态向量，A(t)为状态转移矩阵，G(t)为系统噪声系数矩阵，W(t)为系统噪声向量。

4.2 对准系统量测方程

1）惯性/北斗组合量测信息：选择捷联惯导系统导航解算得到速度和北斗卫星导航系统测量得到速度的差值作为一组量测信息。误差均考虑为白噪声。捷联惯导系统和北斗卫星导航系统的速度信息可分别表示为vI、vG，则速度量测方程为：

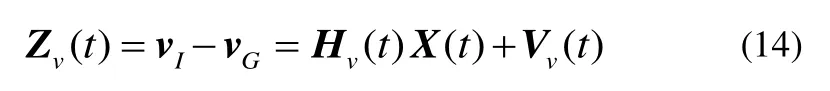
2）运动约束虚拟量测信息：基于运动学约束模型，根据飞机运动的特点，构建虚拟量测信息作为另一组量测信息。第2节中进行了详细的推导，得到式(9)所示的角速度虚拟量测方程。

采用运动模式判别方案检测到飞机处于非角运动状态时，式(14)和式(9)共同构成量测方程，利用Zv(t)和Zω(t)进行量测更新。当检测到飞机发生了角运动时，即对角速度约束辅助进行隔离，仅利用Zv(t)量测更新。

5 基于运动学约束模型辅助的空中动基座对准算法仿真验证分析

为验证本文提出的基于模式判别的运动约束辅助空中动基座对准算法的有效性，对多种典型机动方式进行仿真分析。研究发现，气流场对不同类型飞机的角速度影响有较大差异，根据对某型飞机相关气流场影响的分析，在仿真过程中采用10-3(°)/s数量级的白噪声模拟气流场对角速度的影响。

5.1 仿真条件及高机动下对准结果

捷联惯导系统的陀螺仪直接固联在载体上，其工作环境恶劣，因此陀螺仪和加速度计误差应考虑一阶马尔可夫过程。仿真参数设置见表1所示。

机动轨迹：在0～20 s进行加速，加速度为4 m/s2；在 20～24 s进行加速拉起，加速度为 5 m/s2，俯仰角速度为 7.5 (°)/s；在 64～68 s改平，俯仰角速度为-7.5 (°)/s；在78～81 s倾斜预转弯，横滚角速度为10 (°)/s；在81～141 s转弯，航向角速度为1.5 (°)/s；在141～143 s改平，横滚角速度为-10 (°)/s。其三维轨迹图见图2，该轨迹中，载体姿态机动较多，基本涵盖飞机空中飞行的常规角运动模式。

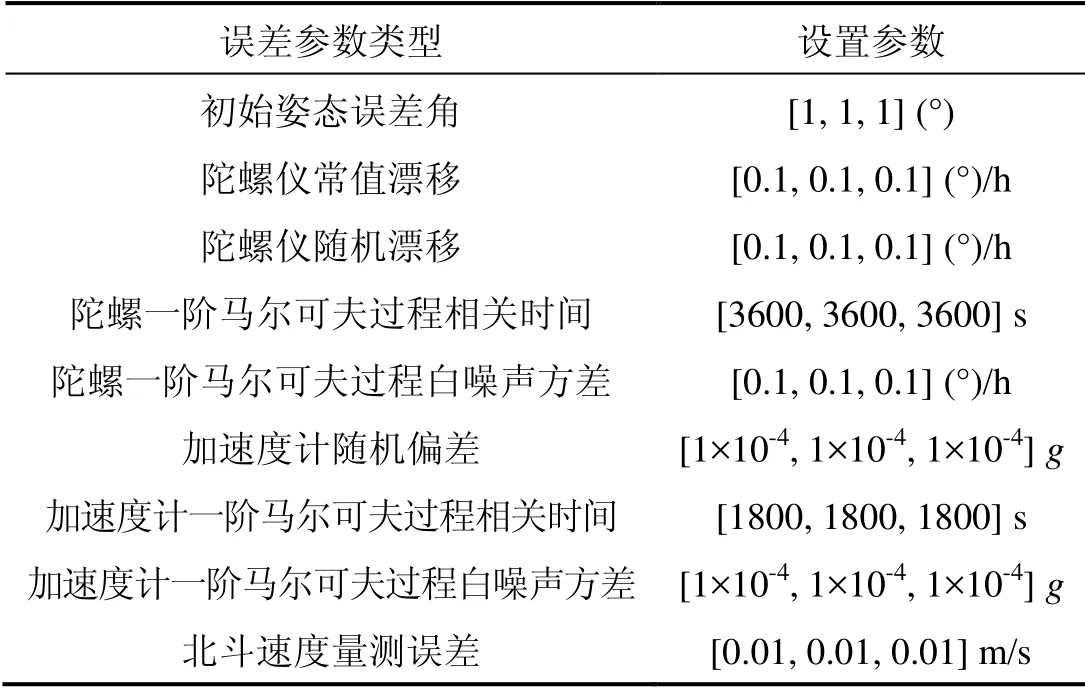
表1 仿真参数Tab.1 Simulation parameter

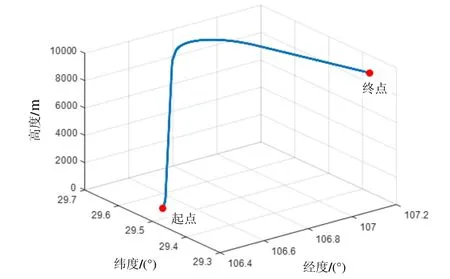
图2 三维航迹图Fig.2 Three-dimensional track

采用本文第3节的角运动判别方案对载体飞行模式进行判别，在本文选用的惯性器件精度条件下，进行大量的数据分析，选取较为合适的阈值为TD=15 000。由于角运动集中在前150 s内，因此给出前200 s的相关曲线。角运动模式检测函数及放大图见图3(a)和图3(b)，判别结果见图3(c)。

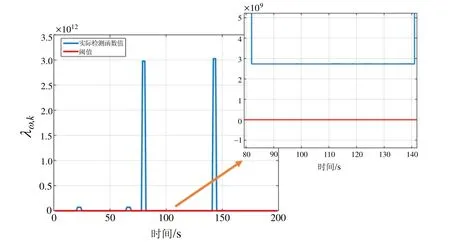
图3 (a)角运动模式检测函数Fig.3 (a) Angular motion mode detection function

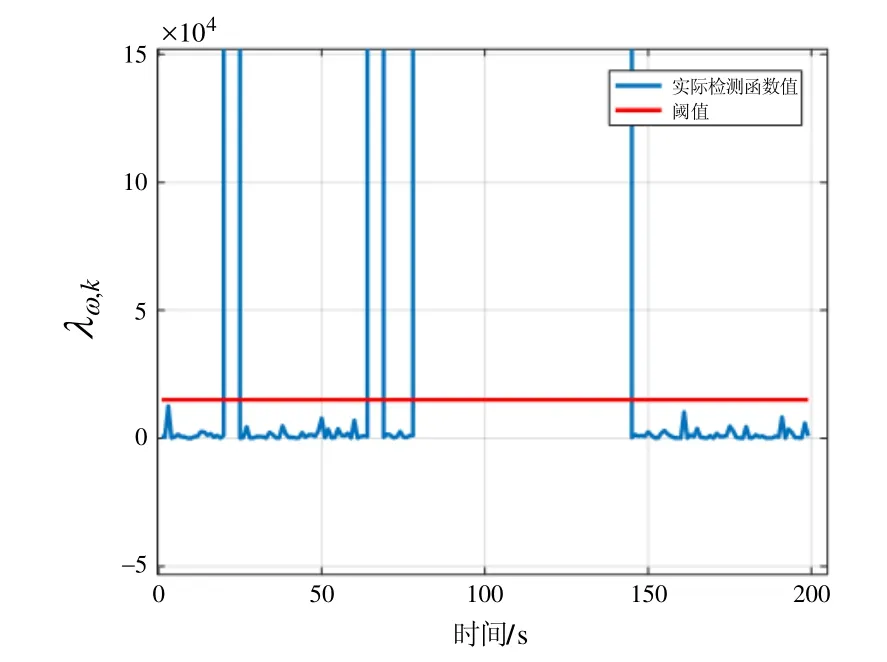
图3 (b)角运动模式检测函数放大图Fig.3 (b) Magnified view of angular motion mode detection function

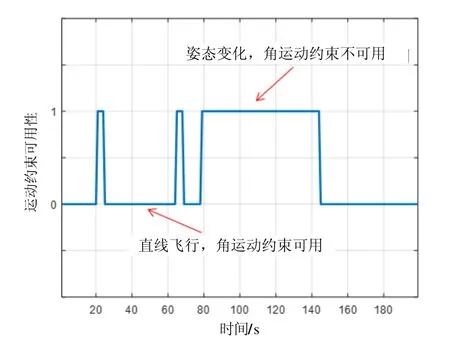
图3 (c)角运动判别结果Fig.3 (c) Discriminant result of angular motion

由图3(a)～(c)可以看出，本文提出的基于残差的运动判别方案，可以有效判断出飞机处于非角运动状态的时间区间，从而在恰当时刻引入角速度约束状态时。考虑地球自转、载体在地球表面运动以及气流场所产生的角速度影响，检测函数值在104量级，而载体处于角运动状态时，检测函数值急剧增大，瞬时达到109次方以上，说明本方法可有效地将载体的角运动检测出来，将地球自转和载体在地球表面运动所产生的角速度分量视为量测信息的噪声信息进行处理是可行的。

总的来看，铜仁市由于中低云量偏多，多阴天及阴雨天气，日照时数大部分地区在1 100～1 300小时之间，日照较少，是全国日照低值区之一。但由于季节分布的不均匀性，秋收作物生育期光照条件比较好，光能的有效性高，能满足花生生长需要。

根据飞机角运动模式的判别结果，在非角运动状态下，采用本文提出的基于运动学约束辅助的北斗卫星导航系统空中动基座对准方法对捷联惯导系统失准角进行估计，选择仅利用北斗卫星导航系统信息的动基座对准算法作为对比进行分析验证。滤波过程中对惯导系统进行闭环校正，通过误差校正后的姿态与真实姿态作差（即姿态角误差）对比分析。姿态误差曲线如图4所示，其中“运动约束+北斗辅助对准”是指采用本文所提出的基于模式判别的运动学约束辅助后的空中动基座对准方法，“北斗辅助对准”是指仅用北斗卫星导航系统辅助的空中动基座对准算法。

图4 高机动下两种对准方法姿态误差曲线Fig.4 Attitude error curves of two alignment methods under high maneuvering

在对准600 s至650 s的时间内，两种对准方法的均值和标准差雷达图如图5所示。

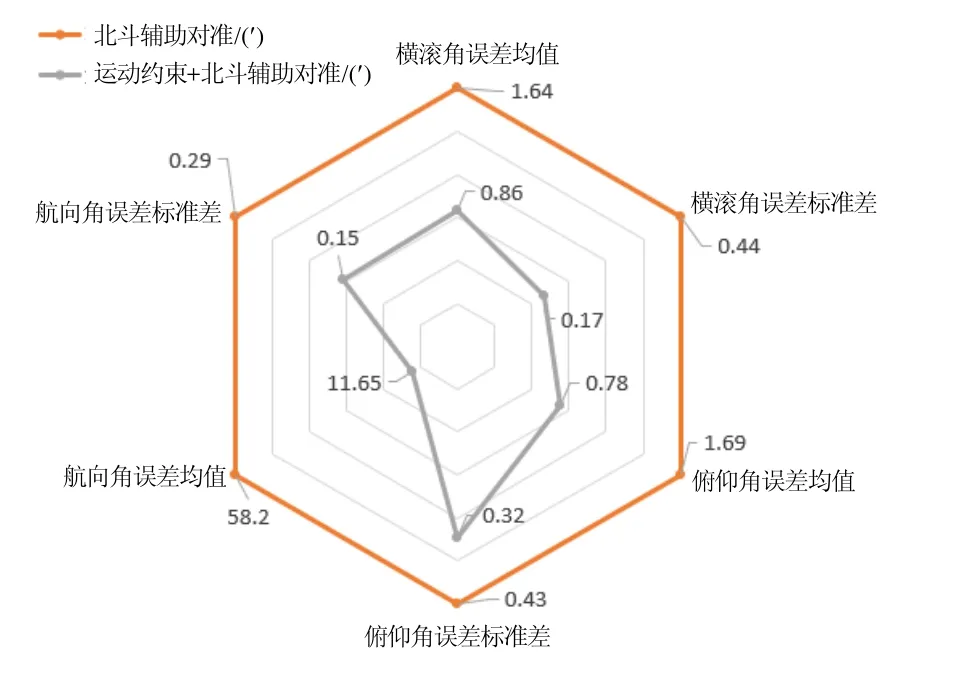
图5 两种对准方法性能对比雷达图Fig.5 Radar chart of performance comparison on two alignment methods

可以看出，载体在对准期间多次进行姿态机动，对于采用速度信息作为外观测量进行匹配的北斗辅助空中动基座对准，一方面增强了航向角的可观测性，机动结束后航向角对准精度得到提高，另一方面当载体作机动飞行时，卡尔曼滤波会产生较大的滤波误差，对准的快速性受到影响，稳定时间较长，在550 s左右横滚角和俯仰角收敛到4′以内。在较长的稳定时间内，航向角可观测性较低导致其误差再次增大，而卡尔曼滤波在滤波达到稳态时会对误差失去敏感性。

本文所提出的方法对准精度和快速性均有了明显提升，横滚角和俯仰角在 400 s左右均可收敛到4′以内，航向角在450 s左右收敛并保持在15′以内。且由图5可知，在相同的对准时间内，本文方法可以达到更高的对准精度。

5.2 多种机动条件下对准结果

由于飞行轨迹对状态变量的可观性有直接的影响，载体机动飞行的轨迹与对准精度关系十分密切。因此在多种典型机动方式下进行对准解算，以验证本文方法的适用性。受本文篇幅所限，仅给出对准的姿态精度。

机动1：加速机动，在10～50 s进行加速，加速度为5m/s2。姿态误差曲线如图6(a)所示。

机动2：匀速机动，载体匀速直线飞行。姿态误差曲线如图6(b)所示。

机动3：蛇形机动，载体在10～20 s进行一组蛇形机动，角速度为5 (°)/s。姿态误差曲线如图6(c)所示。

上述三种机动条件下，两种对准方法的航向角对准时间和对准精度的雷达图如图7所示，其中匀速机动条件下，仅采用北斗辅助的空中对准方法航向角不收敛，此处采用初始航向误差角（60′）作为其对准精度，仿真时间（150 s）作为其对准时间进行绘图。

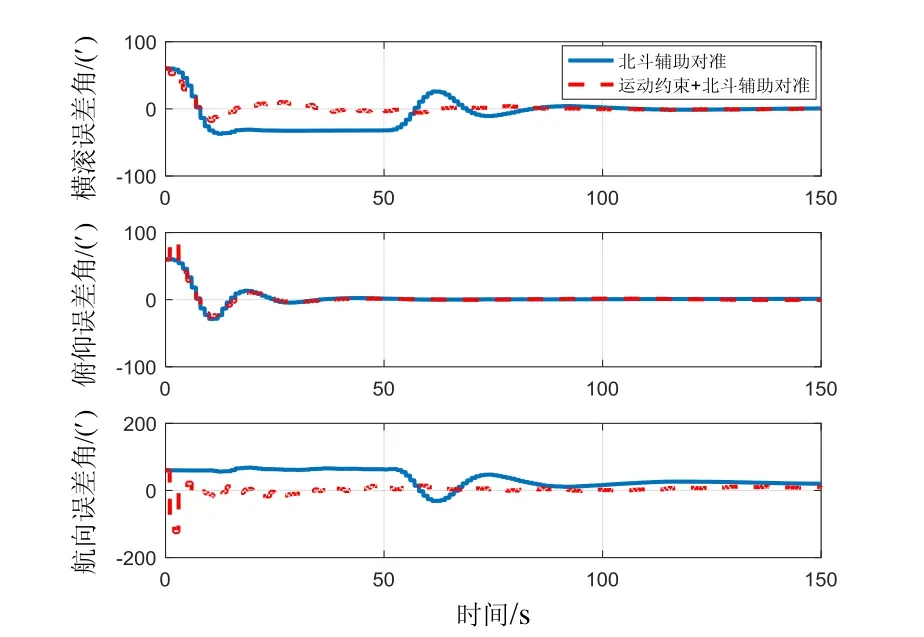
图6 (a) 加速机动下两种对准方法姿态误差曲线Fig.6 (a) Attitude error curves of two alignment methods under acceleration maneuvering

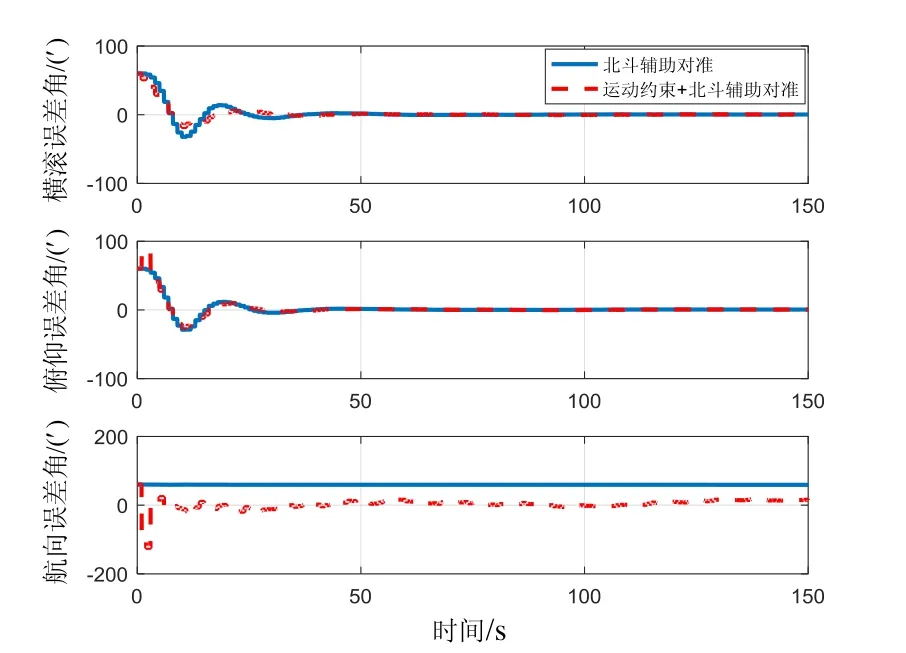
图6 (b) 匀速飞行下两种对准方法姿态误差曲线Fig.6 (b) Attitude error curves of two alignment methods under uniform-velocity flight

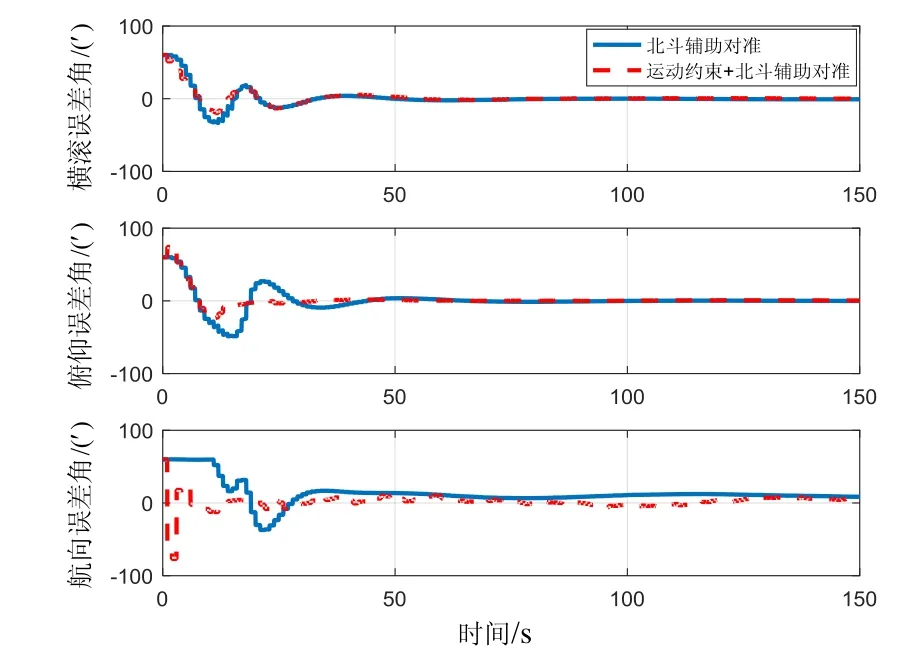
图6 (c) 蛇形机动下两种对准方法姿态误差曲线Fig.6 (c) Attitude error curves of two alignment methods under snake maneuvering

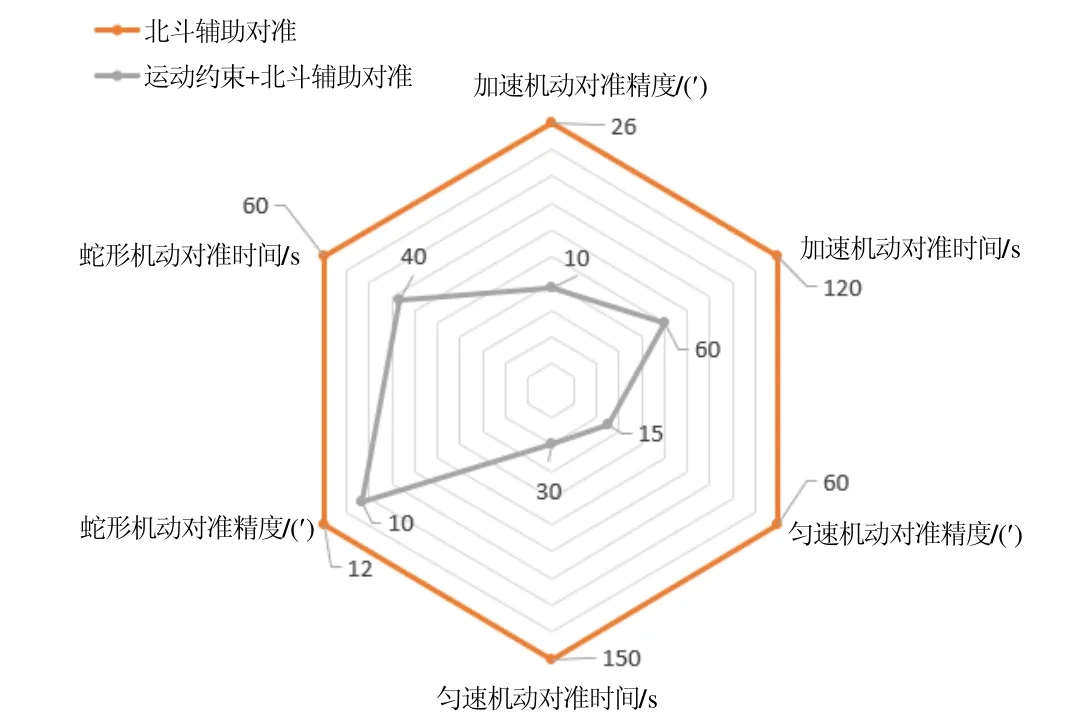
图7 多种机动方式下航向角对准性能雷达图Fig.7 Radar chart of heading angle alignment performance under multiple maneuver modes

可知：1）在多种机动方式下，采用本文提出的基于运动学约束辅助的北斗空中动基座对准方法，均可以显著提高对准的快速性及对准精度，尤其是航向角的对准性能。这是因为本文方法在北斗辅助的基础上增加了角速度约束辅助量测信息，航向角的可观测性提高，因此在稳定性和精度方面都优于仅采用北斗辅助的空中动基座对准。2）在匀速直飞时（加速机动前20 s以及匀速机动全程），采用速度信息作为外观测量进行匹配的北斗辅助空中动基座对准，方位失准角不可观，因此航向角完全不收敛。而本文方法中角速度约束虚拟量测信息的引入，增加了方位失准角的可观测性，在匀速直飞运动下，航向角也迅速收敛，显著改善了其对准精度和快速性。

6 结 论

为了提高飞机快速反应能力，优化初始对准性能，在传统北斗辅助捷联惯导系统进行动基座初始对准架构下，提出基于残差的角运动模式判别方案，在此基础上研究提出一种基于运动学约束模型辅助的空中动基座对准方法。在多种机动方式下验证该方案的可行性及空中动基座对准性能。仿真验证结果表明：采用本文提出的基于运动学约束辅助的北斗空中动基座对准方法，各种机动条件下均可显著提高对准的快速性及精度。在典型的加速机动下，本文方法与仅采用北斗信息的空中动基座对准相比，航向角对准时间由120 s缩减至60 s，对准精度由26′提升至10′。本文提出的方法在不增加传感器的前提下，优化了空中动基座初始对准性能，对工程应用具有重要的参考价值。