冬季黑潮延伸体区域涡旋尺度海面温度季节内变化特征❋

杨小绘，贾英来

(中国海洋大学海洋与大气学院 海洋气象学系，山东 青岛 266100)

黑潮延伸体区域是中纬度海洋-大气相互作用的关键区域[1-2]。Wang等[3]发现黑潮延伸体区域大尺度的海面温度异常存在季节内变化特征，并且通过海-气相互作用驱动北太平洋海盆尺度的风应力旋度，构成耦合模态，该季节内振荡信号在夏季最强。黑潮延伸体区域海洋涡旋活跃，涡旋通过海气相互作用影响其上层大气。而海气相互作用的关键是海-气界面间的热通量交换，热通量和SST间的关系在不同空间尺度(比如大尺度和涡旋尺度)上并不相同，Li等[4]用惩罚回归分析(Penalized spectral regression,PSR)得出湍流热通量和SST异常的关系在涡旋尺度(<1 000 km)上同位相变化且关系密切，是涡旋尺度SST强迫大气；而在海盆尺度上，热通量和SST呈负相关[5-6]，这时为大气强迫海洋。Smirnov等[7]和Putrasahan等[8]通过利用数值模式也得到类似结论。

前人发现海洋涡旋可以引起海气界面热量通量以及边界层大气中风速等要素的响应[9-10]，该响应在冬季最强[11-12]，其主要通过垂直混合机制影响大气[13-15]。通过涡旋合成的方法[16-18]发现湍流热通量异常在涡旋中心附近更强，在涡旋外部最小[17]。在暖涡上空风速增大，冷涡上空风速减小[18]。并且涡旋对大气的影响存在季节变化，冬春最大、夏秋较弱[11]。但是，前人研究海洋涡旋上空的海-气相互作用过程时，多通过涡旋合成的方法来进行，并未探讨其时间变化特征。黑潮延伸体区域的流轴弯曲(Meander)存在3～60 d的季节内变化信号[19]，该季节内变化信号是否也存在于涡旋尺度SST的时间变化之中？为探讨黑潮延伸体区域涡旋尺度SST的时间变化特征，本文利用观测资料和再分析资料对大尺度和涡旋尺度SST的时间变化进行了分析，比较了两者在季节内变化上的区别，并进一步分析了和冬季涡旋尺度SST季节内变化相关的大气边界层的响应特征。

1 资料和方法

本文所用SST 数据有欧洲中期天气预报中心ECMWF(European center for medium-range weather forecasts)的再分析资料ERA-interim SST数据(水平分辨率为0.75°×0.75°，时间间隔为6 h)和OISST(NOAA Optimum Interpolation Sea Surface Temperature,OISST)观测数据(水平分辨率为0.25°×0.25°的逐日数据)。取两者共同的时间段(2002年1月～2017年间)进行研究。因ERA数据不仅包含SST，而且包含大气边界层的各变量，本文中主要选取ERA的数据集进行分析。本文中冬季定义为每年的11月1日～次年3月31日，夏季定义为每年的5月1日～9月30日。根据黑潮延伸体区域海洋涡旋和锋面的特征尺度[20]，采用5°×5°二维空间滤波(2D Boxcar)方法分离涡旋尺度的SST异常和大尺度的SST异常信号。利用小波功率谱分析方法研究时间变化显著周期，采用Lanczos带通滤波器对资料进行带通滤波以得到相应的频段。为对季节内时间变化信号进行研究，所有数据均进行去(2002—2017年)气候态月平均处理后再进行相应的后续处理。

采用ERA-interim再分析数据的海表面潜热通量(Surface Latent Heat Flux,SLHF)、海表面感热通量(Surface Sensible Heat Flux,SSHF)、蒸发(Evaporation,E)、10 m风场(10 metre speed,SPE)、2 m气温(2 metre temperature,2mT)等数据分析大气边界层对SST信号的响应。采用与SST相同的方法对大气边界层各变量进行涡旋尺度信号和大尺度信号的分离。为考察涡旋尺度SST异常信号引起的大气边界层响应，采用二维模态相关(Pattern correlation)的方法进行分析两者在空间分布形态上的一致性。关于涡旋引起的大气的响应，以前的文献主要通过涡旋合成分析[9-10,16-19]，但是涡旋合成后的场是多涡旋平均的结果，并不能探讨涡旋及大气响应两者关系的时间变化。模态相关，即两个变量之间的线性相关的Pearson积矩系数(Pearson product-moment coefficient)用于衡量两个变量各自模态之间的相关性。其主要适用于分析两个异常场空间分布形态的异同。若两个异常场(比如涡旋SST异常场和SLHF异常场)各异常中心的位置和形状近似，则相关系数高。利用模态相关可以研究涡旋SST异常信号引起的大气异常响应。若两者相关系数大，则说明涡旋SST异常能够引起大气变量在空间同位相的响应。模态相关系数的时间变化还可以显示大气对SST异常响应的时间变化。在本文中，我们将利用模态相关分析揭示涡旋SST异常及大气响应的季节内变化特征。

2 涡旋尺度海面温度季节内振荡的时空分布特征

为说明黑潮-亲潮延伸体区域大尺度海温与涡旋尺度海温在季节内变化特征上的不同，图1给出了SSTA(Sea Surface Temperature Anomaly)场90 d滑动标准差在冬季、夏季的空间分布。两种数据的结果都表明，大尺度SST的季节内信号具有夏季强、冬季弱的特点(见图1(a)、(c)及(e)、(g))，其中大尺度SST季节内变化信号的空间分布和Wang 等[3]的结果一致。涡旋尺度SST的季节内变化信号则是冬季强、夏季弱(见图1(b)、(d)及(e)、(f))。大尺度和涡旋尺度SST季节内信号标准差的空间分布也不相同，涡旋尺度信号主要分布在黑潮-亲潮海洋锋面区域，在日本沿岸最强，并沿黑潮、亲潮锋面向东延伸。在两个数据中冬季涡旋尺度SST信号的标准差可达1 ℃左右，尤其是在黑潮、亲潮锋面区域，是SST的主要变化信号。OISST数据中涡旋尺度季节内信号的标准差更大可能是因为其分辨率高的原因。

为进一步考察涡旋尺度季节内信号的变化周期，选取黑潮海洋锋面上的一点(146.75°E，36.25°N)，对其SST时间序列进行小波分析(见图2)。大尺度SST的显著周期以20～40 d为主，而涡旋尺度SST的显著周期则在40 d以上，两者的小波谱值均存在明显的季节变化。为进一步考察黑潮-亲潮延伸体区SST的季节内变化周期，分0～40 d和40～100 d两个季节变化显著的频段进行研究，图3给出了两个频段内大尺度和涡旋尺度SST信号在夏季和冬季期间小波谱值最大值的空间分布，以考察该频段周期信号的特征。对于大尺度SST信号，0～40 d频段的小波谱值主要在日本沿岸较强，而40～100 d频段的信号还多分布在黑潮延伸体下游。大尺度SST信号的0～40 d变化和40～100 d信号均在夏季最明显(见图3)，这和Wang 等[3]关于该区域大尺度SST季节内变化的结论一致。对于涡旋尺度SST变化信号，40～100 d频段的小波谱值(约15～20 ℃2)明显强于0～40 d频段的(6 ℃2以内)(见图4)，并且涡旋尺度SST的季节内变化在冬季明显强于夏季。冬季涡旋尺度SST的40～100 d振荡的显著信号主要分布在黑潮、亲潮海洋锋面处 (见图4)，这可能和黑潮流轴弯曲(Meander)中的季节内信号有关[19]。

3 冬季涡旋尺度海面温度的季节内变化信号对边界层大气的影响

由上述可知，大尺度SST与涡旋尺度SST的季节内振荡信号并不一致，在冬季，黑潮-亲潮延伸体区域SST变化主要是涡旋尺度SST的40～100 d变化造成的。根据前人研究[9-10]，涡旋尺度SST变化可以引起海气界面热量通量以及边界层大气中风速等要素的响应，那么，涡旋尺度SST的季节内变化能否引起大气边界层各要素的相应变化呢？为回答这个问题，本文首先考察了黑潮锋面一点(146.75°E，36.25°N)上的SLHF的小波功率谱分布(见图2(e)、(f)、(g)、(h))。

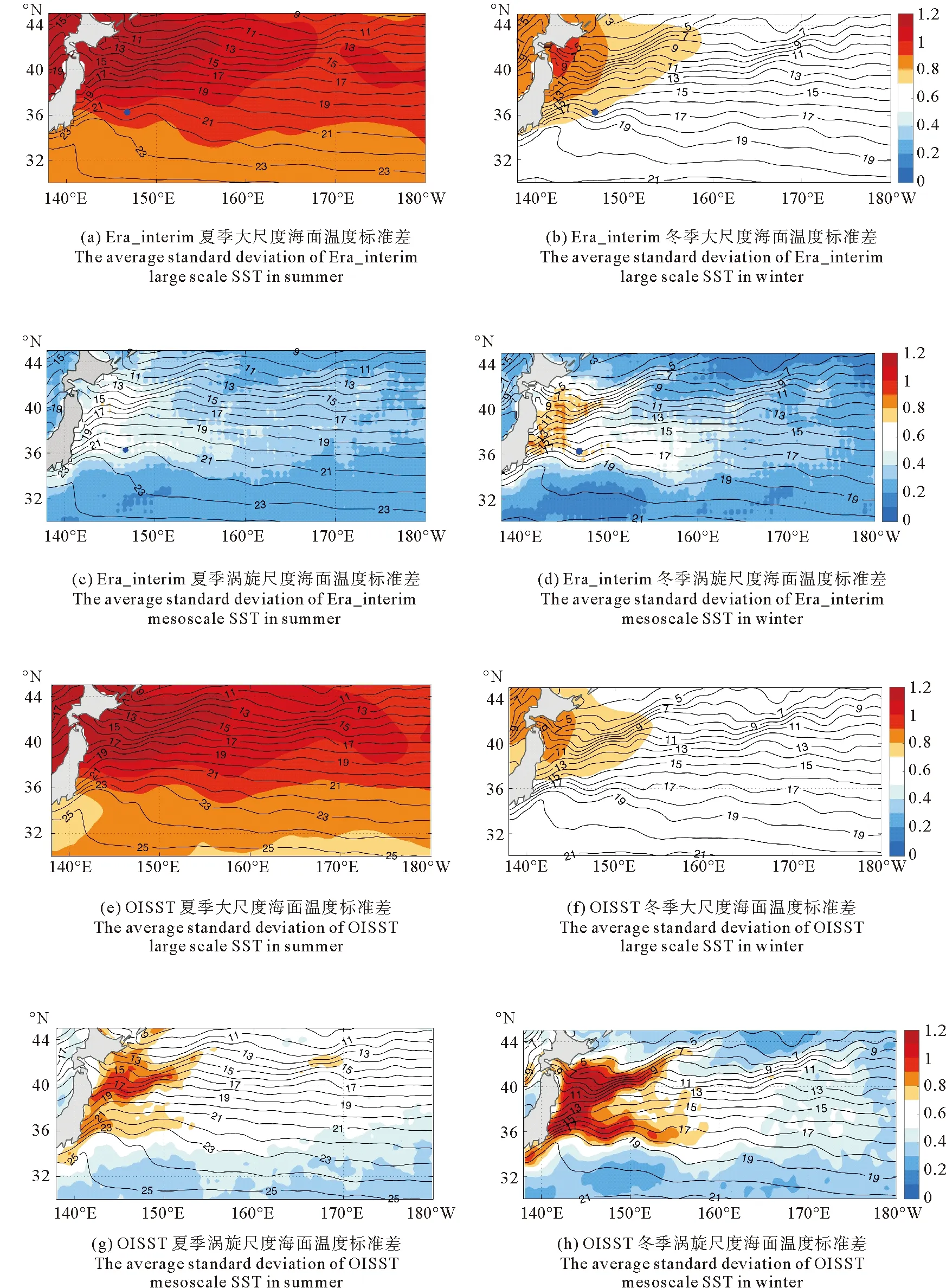
(填色部分为海面温度90 d滑动平均的标准差，等值线为相应季节的海面温度多年平均气候态值(单位：℃)。图中的蓝色点为下文分析中选取的点(146.75°E，36.25°N)。The shaded parts are 90-day running mean standard deviation of SST and the contours are climatological distribution of SST，(Unit:℃.) The blue point (146.75°E,36.25°N) indicate the token point for the following analysis.)
图1 海面温度标准差图
Fig.1 The average standard deviation distribution of SST

((a、c、e、g)中黑色等值线圈住的填色区域为通过95%信度水平的小波功率谱值，黑色虚线为影响锥的部分曲线，黑色曲线内为可信区域。(b、d、f、h)中蓝色实线为小波全谱，红色虚线为95%信度水平的标准红噪音谱。The dotted lines in (a,c,e,g) are part of conial and the conial area is the credible part;The solid line is the period that passes the 95% confidence level.Solid lines in (b,d,f,h) represent the wavelet full spectrum of the oscillation,and the dashed lines indicate the standard red-noise spectra at the 95% confidence level.)
图2 点(146.75°E，36.25°N)的小波功率谱以及小波全谱图
Fig.2 Wavelet spectrum and wavelet full spectrum on the point (146.75°E,36.25°N)

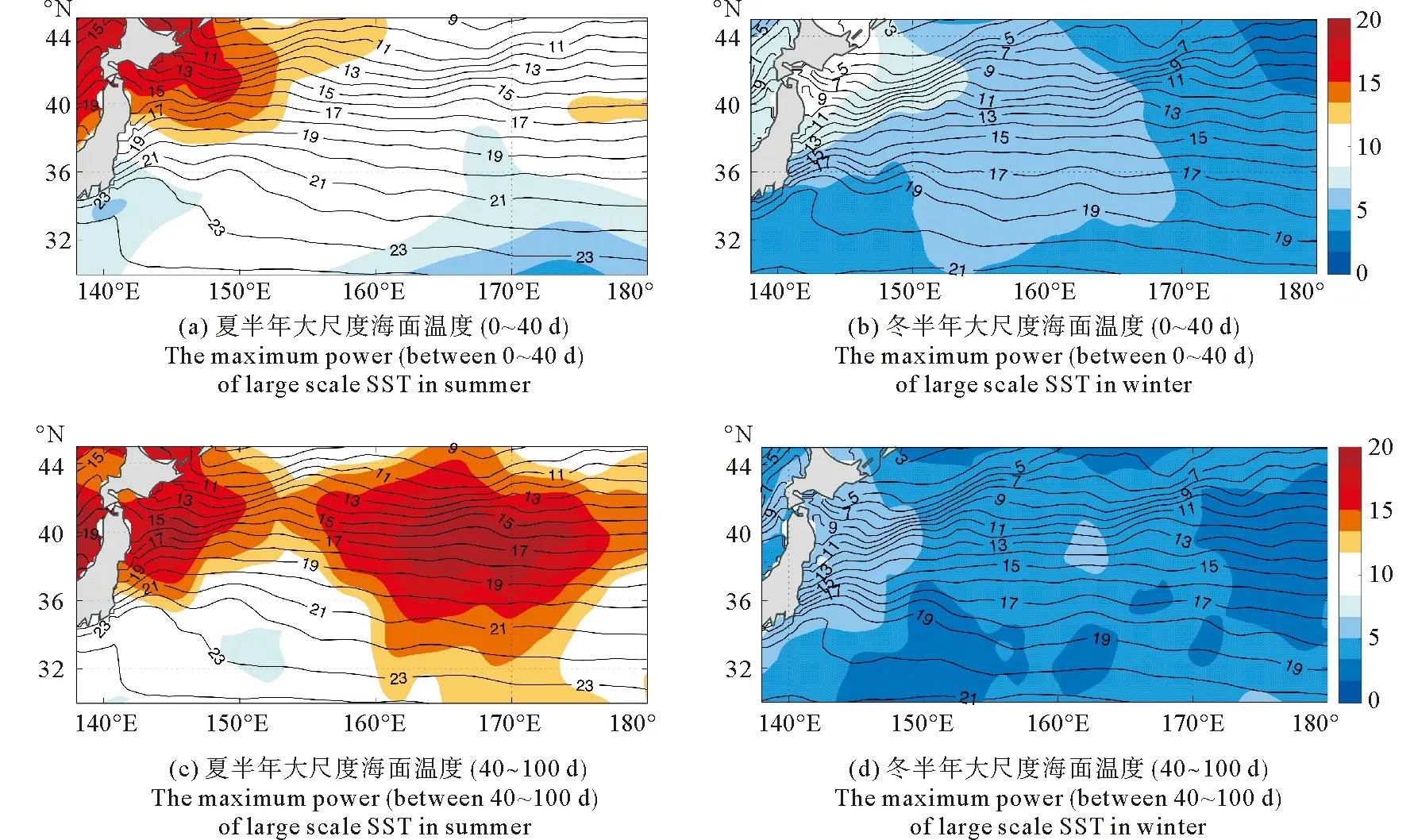
(填色部分为大尺度海面温度的小波全谱的最大谱值，单位：℃2，等值线部分为相应季节的多年海面温度平均值，单位：℃。The shaded parts are maximum wavelet full spectrum power of SST (Unit:℃2) and the contours are climatological distribution of corresponding SST (Unit:℃).)
图3 大尺度海面温度的小波全谱最大谱值平面分布图
Fig.3 Distribution of the large scale SST maximum wavelet power

(图中的实线方框为下文分析所选取的关键区域，范围为(142°E～160°E,33°N～44°N)。The rectangle indicate the key region for the following analysis:(142°E～160°E,33°N～44°N).)
图4 同图3，但填色部分为涡旋尺度海面温度
Fig.4 As in Fig.3,but for mesoscale SST

由图可见，大尺度SLHF及涡旋尺度SLHF均存在季节内振荡，大尺度SLHF的显著周期以40 d以上为主，峰值在60～70 d。涡旋尺度SLHF的显著周期也具有60～100 d的显著周期，两者的小波谱值均存在明显的季节变化。其中涡旋尺度SLHF与涡旋尺度SST的功率谱结构相似。

为进一步探讨涡旋尺度SST和SLHF在季节内变化上的相关性，将冬季涡旋尺度SST和大气边界层各要素的异常进行20～100 d带通滤波以提取季节内变化信号，并对其进行区域平均后(142°E～160°E，33°N～44°N)计算了超前滞后相关系数(见图5)。为和大尺度信号进行对比，同时给出了大尺度SST和大气边界层各要素间的相关关系。图5明确表明，大尺度SST与大气边界层各要素间的相关性比涡旋尺度信号间的相关性弱得多。大气边界层各变量和SST相关系数低且呈现SST超前或滞后的相关(大气强迫海洋)。而涡旋尺度SST信号则和SLHF、SSHF、BLH、E，TSA以及SPE都是同期相关，并且涡旋尺度SST信号和SLHF、SSHF、BLH、E，TSA以及SPE这几个变量间的同期相关系数高达0.8。两者涡旋尺度信号的变化一致性与前人用涡旋追踪合成方法得出的结果一致[9-10,16-19]。这说明冬季涡旋尺度SST信号能够引起大气边界层各要素的同期响应，冬季，黑潮延伸体区域，在涡旋尺度上，是海洋SST驱动大气。

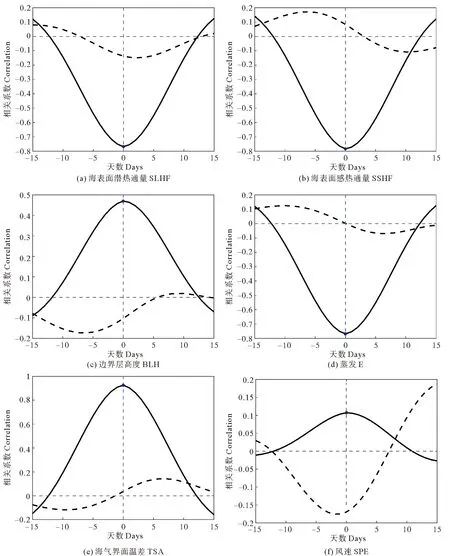
(黑色实线为涡旋尺度SST与涡旋尺度大气要素的超前滞后相关系数，黑色虚线为大尺度SST与大尺度大气要素的超前滞后相关系数。The solid line and;Dashed line indicate the mesoscale and large scale,respectively.)
图5 冬季(142°E～160°E,33°N～44°N)区域内平均的海面温度与大气要素的超前滞后相关
Fig.5 Lead lag correlation between area-mean SST and atmospheric elements in the key region (142°E～160°E,33°N～44°N) during winter

上文发现冬季涡旋尺度SST存在季节内变化信号，当涡旋尺度SST发生变化时，大气要素产生与之一致的响应。前人关于涡旋引起大气的响应主要通过涡旋合成分析[9-10,16-19]，但是涡旋合成后的场是多涡旋平均的结果，这并不能探讨大气对涡旋的响应是否随着涡旋SST信号的时间而产生相应的变化。那么涡旋尺度SST的季节内信号能否引起与大气响应的季节内变化？

为回答这个问题，本文使用二维模态相关分析来研究这两者之间的时间变化关系。冬季(142°E～160°E，33°N～44°N)的涡旋场与大气边界层各要素响应的时间变化关系如图6蓝色实线所示。由图可见，对与涡旋尺度SST同位相时间相关密切的热通量、蒸发和海气温差项，模态相关系数同样较强，高达0.8以上，可见两者在空间分布上也非常一致。而边界层高度和海面风场与涡旋尺度SST的关系则较差。这说明涡旋尺度SST的季节内变化信号能够引起大气边界层各要素，尤其是热通量的相应的季节内变化。同时，两者的模态相关系数的时间变化也说明在有的年份，两者的关系较好，在有的时间段，两者的关系较差。那么大气边界层对涡旋尺度SST异常的响应强度与什么因素有关系呢？为此，统计了上述区域较强涡旋(即暖涡中心值>0.6 ℃与冷涡中心值<-0.6 ℃)总个数的时间变化(见图6黑色实线)。可以看到较强涡旋的个数与大气对SST异常响应密切相关，强涡旋多的时候大气边界层异常与SST异常在空间分布上更一致，这时候由大气边界层更多地受涡旋SST的影响，而涡旋少的时候大气边界层对涡旋SST异常的响应较弱。图6红色实线给出的是点(146.75°E，36.25°N)涡旋尺度SST变化在40～100 d频段内的小波功率谱值时间变化序列，可以看出，涡旋SST季节内变化信号明显的时间段模态相关系数较大，强涡个数较多；而涡旋SST季节内变化信号不明显的时间段，强涡个数较小，模态相关系数也较小。这说明涡旋SST季节内变化表现为强涡个数的变化，而强涡的增多也加强了大气边界层的响应。Shan和Dong[21]利用WRF(Weather research and forecasting model)模式理想试验的结果揭示了SST异常信号的增强会加强大气的响应，这和我们的结果是一致的。为更直观地进行验证，以SLHF为例，选取了6个不同的时间做了分析。参见图6(a)中的3个红点(代表模态相关系数大值点)和3个绿点(代表小值点)。图7给出了这6个时间的涡旋SST场以及SLHF场的空间分布。由图可见，在涡旋SST较弱的时间，大气的涡旋尺度异常信号仍然存在但是分布位置和形态与涡旋SST并不一致，较弱的涡旋不易对大气边界层产生影响。而较强涡旋上空则大多会出现海表面热通量的响应。并且强涡旋大多沿着黑潮、亲潮锋面分布，这与图1(d)涡旋尺度SST季节内信号沿锋面分布也是一致的。总之，较强涡旋少的时候模态相关系数低，较强涡旋多的时候模态相关系数高。在该区域较强涡旋信号个数较多的时间段,SST异常的季节内变化更明显，大气与涡旋尺度SST信号的相关程度更大。

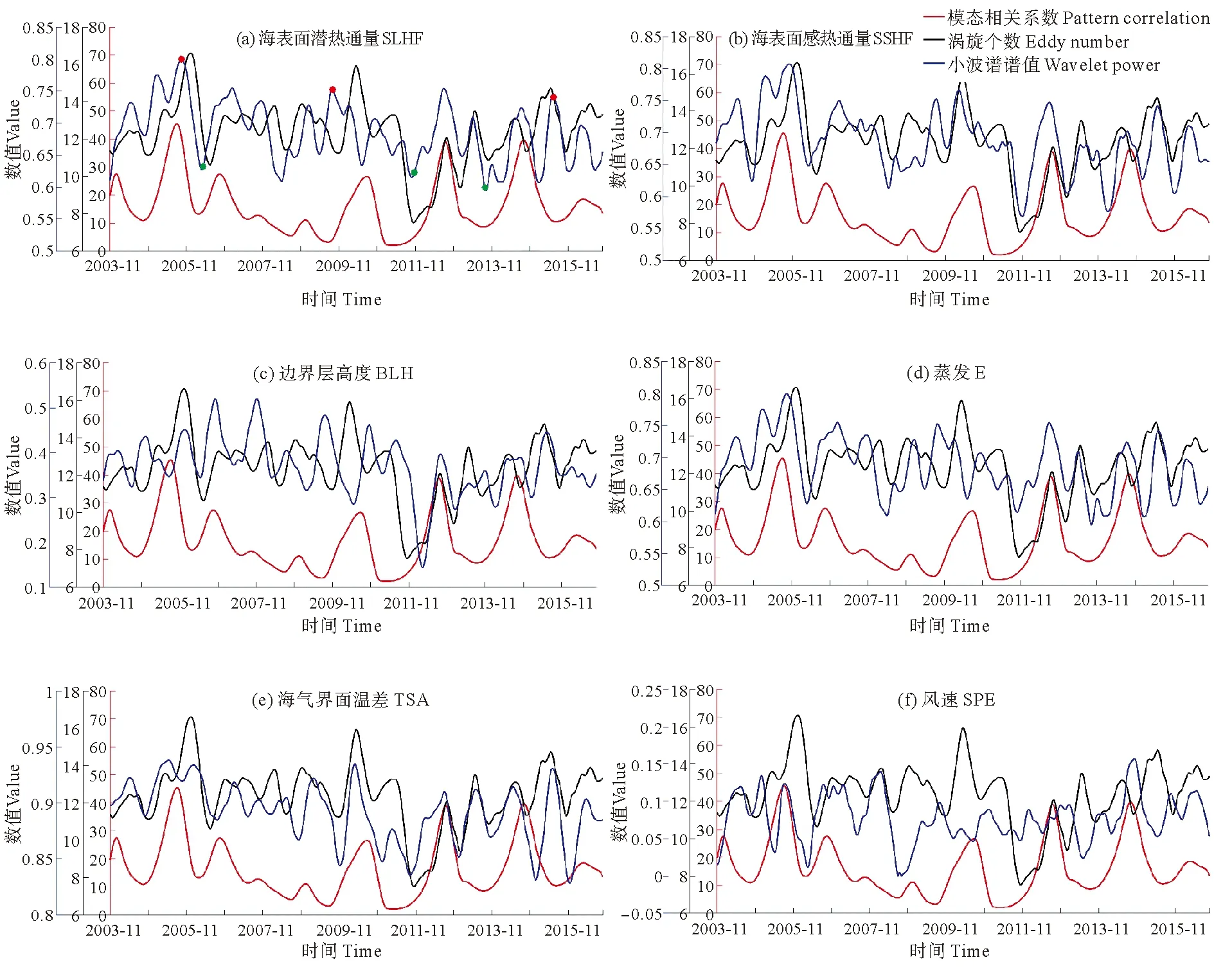
(蓝色纵轴代表关键区内涡旋尺度海面温度与大气各要素模态相关系数90 d滑动平均的大小，黑色纵轴代表关键区内较强涡旋的个数，红色纵轴代表点(146.75°E,36.25°N)40～100 d小波谱的平均谱值。(a)中的三个红点代表模态相关系数的高值点，三个绿点代表模态相关系数的低值点。The blue solid lines indicate 90 d running mean pattern correlation curves between mesoscale SST and atmospheric elements in the key region.Black lines indicate the number of more stronger eddies (the centers maximum of warm eddies more than 0.6 ℃ and the centers minimum of cold eddies less than -0.6 ℃) 90 d running mean curves in the key region (142°E～160°E,33°N～44°N).Red lines indicate the SST mean power between 40～100 d on the point (146.75°E,36.25°N)90 d running mean curves.In (a) the three red points are the high points and the three green points are the low points in the temporal variation of pattern correlation coefficients.)
图6 冬季模态相关系数、较强涡旋个数以及40～100 d的小波谱谱值的时间序列
Fig.6 Times series of pattern correlation,the number of stronger eddies and the mean wavelet power between 40～100 d in winter

(填色部分为涡旋尺度海面温度异常，单位：℃；红蓝等值线为涡旋尺度海表面潜热通量异常(海表面潜热通量正值代表海洋从大气中吸收热量)，单位:W/m2；黑色等值线为冬季的海面温度平均值，单位：℃。(a,b,c)为模态相关系数的高值点，(d,e,f)为模态相关系数的低值点。The shaded parts are mesoscale SST variability and the contours are mesoscale SLHF variability (the positive value of SLHF means downward into the ocean).Distributions of the high points of pattern correlation coefficients are present in (a,b,c) and low points in (d,e,f).)
图7 涡旋尺度海面温度和海表面潜热通量异常的分布图
Fig.7 Distribution of mesoscale SST variability and mesoscale SLHF variability

冬季黑潮延伸体区域盛行西北风，把欧亚大陆的干冷空气吹到温暖潮湿的海洋上，这种情况下，黑潮延伸体区域会有强的向上的湍流热通量释放，从而会对上空大气造成重要影响。这种释放是通过海洋的中尺度结构海洋锋面和海洋涡旋来完成的，所以由海洋涡旋引起的海面温度异常有重要影响。为更进一步验证黑潮-亲潮延伸体区涡旋尺度SST的季节内变化信号会引起SLHF的响应，同样分0～40 d和40～100 d两个季节内变化显著的频段进行研究。图8和9给出了这两个频段内大尺度和涡旋尺度SLHF信号在夏季和冬季期间小波谱值的最大值分布，以考察相应频段周期的强弱。与大尺度SST不一致，大尺度SLHF信号40～100 d频段的小波谱值明显强于0～40 d频段，并且大尺度SLHF信号的40～100 d变化在冬季最明显，信号大值区的分布位置主要在黑潮流轴以南。对于涡旋尺度SLHF变化信号，40～100 d 频段的小波谱值明显强于0～40 d频段，在黑潮、亲潮海洋锋面处，冬季也明显存在40～100 d振荡的显著信号分布(见图9)，与涡旋尺度SST的变化一致。这进一步说明涡旋尺度SST的季节内变化能够引起SLHF的相应变化，使SLHF在黑潮、亲潮海洋锋面处出现相似的季节内变化周期。从SLHF对涡旋尺度SST的响应，可以进一步证实涡旋尺度SST对大气要素的影响较强，冬季涡旋尺度SST的季节内振荡周期以40～100 d周期为主，并且会引起大气边界层的响应，激发海气界面湍流热通量、海面气温、边界层高度等同位相的季节内振荡。

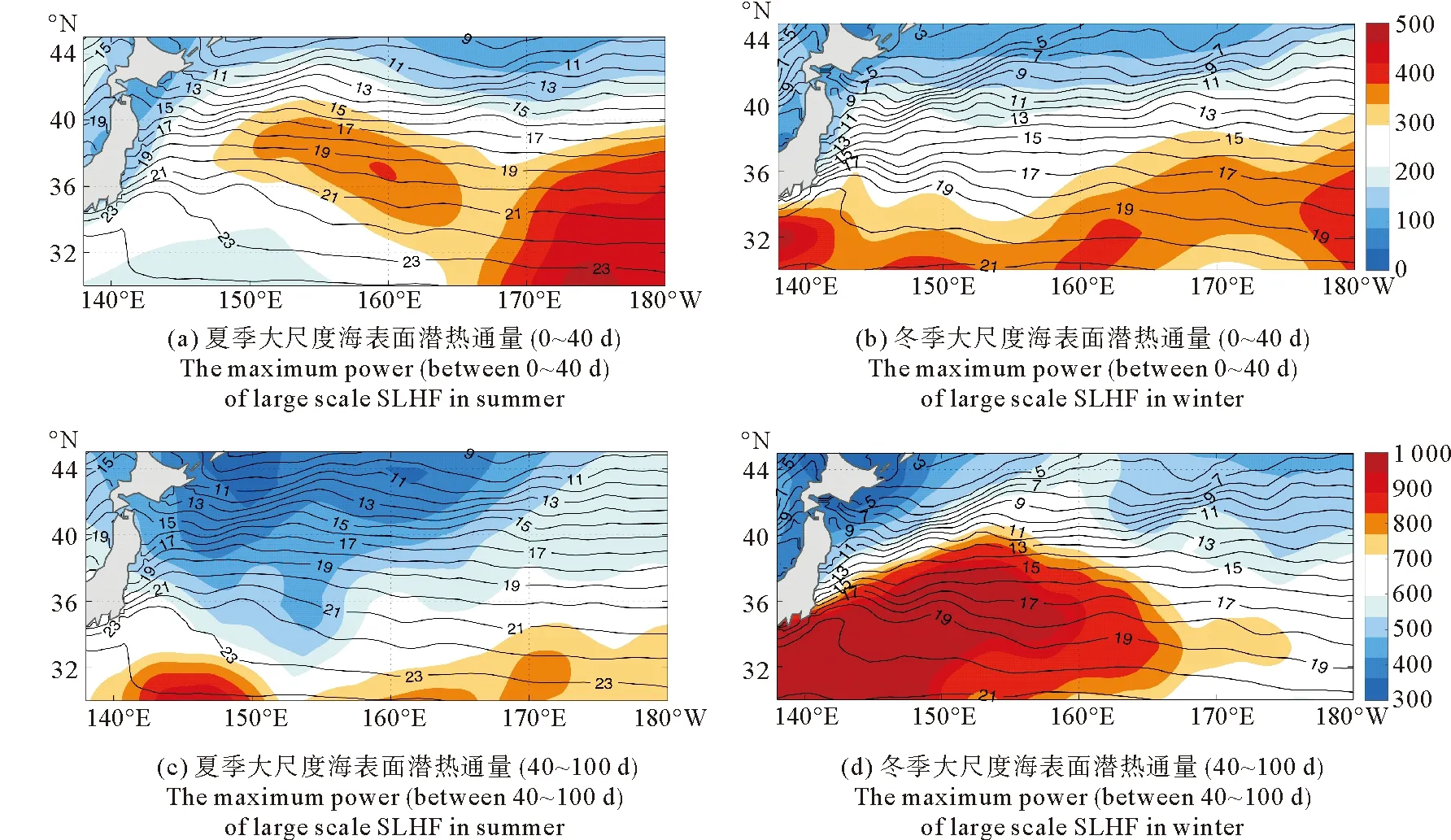
图8 同图3，但填色部分为大尺度海表面潜热通量(单位：(W/m2)2)Fig.8 As in Fig.3,but shaded for large scale SLHF (Unit:(W/m2)2)

4 结论与讨论

本文利用ERA_interim再分析资料以及OISST高分辨率海面温度卫星观测数据，以及小波分析、二维模态相关(Pattern correlation)分析等方法系统地分析了黑潮延伸体区域涡旋尺度SST信号的季节内变化特征及其对边界层大气的影响。结果表明，涡旋尺度SST的季节内变化和大尺度的信号在空间分布和季节变化上均存在显著差别，涡旋尺度SST季节内振荡信号在冬季最强，夏季最弱，而大尺度信号则在夏季最强。涡旋尺度SST季节内变化信号主要分布在黑潮-亲潮海洋锋面区域，在日本沿岸振幅最强，并沿黑潮、亲潮锋面向东延伸，其标准差高达1 ℃，是该海域冬季SST的主要变化信号。涡旋尺度SST的季节内振荡周期以40～100 d周期为主，并且会引起大气边界层的响应，激发海气界面湍流热通量、海面气温、边界层高度等同位相的季节内振荡。强涡旋少的时候涡旋尺度SST信号和海气界面湍流热通量间模态相关系数低，强涡旋多的时候两者模态相关系数高。在黑潮延伸体上游区域强涡个数较多的时间段,SST异常的季节内变化更明显，边界层大气与涡旋尺度SST信号的相关程度更大。

图9 同图3，但填色部分为涡旋尺度海表面潜热通量(单位：(W/m2)2)Fig.9 As in Fig.3,but shaded for mesoscale SLHF (Uint:(W/m2)2)

涡旋尺度SST的季节内变化信号和黑潮延伸体区域的锋面变化以及该区域的海洋涡旋有着密切的关系，那么，该信号是否也存在于海平面高度场中？这是我们今后要研究的问题。另外，该SST变化信号是否能够通过影响大气边界层的变化，尤其是和大气之间的热量通量而进一步影响上层大气也值得研究。