线性回归模型系数变点的在线监测

秦瑞兵,孙 丽,宋冠仪

(1.山西大学 数学科学学院，山西 太原 030006；2.山东大学 数学学院，山东 济南 250100)

0 引言

近年来很多领域存在变点问题，有关突变点理论应用从最初由Page[1]提出在产品质量控制领域扩宽到在金融等领域，如Hoga[2]提出的在线监测多元时间序列在金融上的应用.而快速地监测到一任意时刻出现的变点并报警，对于减小损失，降低风险具有重要意义.

陈希孺[3]与Perron[4]介绍了有关变点理论的研究与发展.有关线性过程的变点估计问题，Bai[5]基于最小二乘估计提出其均值变点的估计.赵文芝等[6]则给出了其方差变点的CUSUM型估计量.随后Zhao等[7]提出采用比率统计量检测线性过程的方差变点.

由实时监测时历史数据不断产生，Chu等[8]提出在线监测方法，即在原模型的基础上，对在线数据连续进行变点检验，当监测统计量的值超过给定极限临界值时停止且当前时刻为变点，否则一直监测下去.Csörgö等[9]提出的变点分析的极限理论也为变点的研究奠定了理论基础.Deng等[10]证明了CUSQ统计量在一般假设下的极限分布.

但上述文献[11-13]中监测方法的准确度和运行长度均依赖于初始样本中的长期方差的估计，故据文献[16-18]监测统计量思考，并基于回归残差的平方累积和统计量，提出两种比值型监测统计量，避免了文献[11-13]中变点监测统计量的样本长期方差的估计，进而提高监测稳定性.

1 监测过程与假设

考虑如下线性回归模型：

(1)

假设前[Tr]个历史样本满足βi=β0，1≤i≤[Tr]，r∈(0,1).从第[Tr]+1个新样本数据开始在线监测系数变点,提出如下假设检验问题：

H0:βi=β0,i=[Tr]+1,[Tr]+2,…

(2)

(3)

其中s*∈(0,1)，模型系数β0,β*,(β0≠β*)和变点的值均未知.

由下节定义的两个监测统计量Γ1(r),Γ2(r)及其相应的显著性水平为α的临界值c1(α),c2(α)定义停时

τ([Tr])=inf{[Ts]>1:Γ1,2(r)>c1,2(α)}其中c1,2(α)满足原假设下lim[Tr]→∞P{τ([Tr])<∞}=α与备择假设下lim[Tr]→∞P{τ([Tr])<∞}=1.

基于文献[11-13]的假设，为证明监测统计量渐近性质及备择假设下的一致性，线性回归模型需满足如下假设条件:

{εi,1≤i<∞}独立同分布.

(4)

(5)

(6)

{εi,1≤i<∞},{xi,1≤i<∞}相互独立.

(7)

存在正定阵C和常数τ>0使得

(8)

2 主要结论

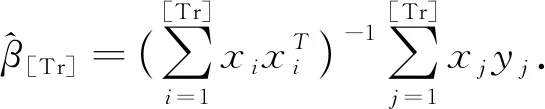
构造一般残差平方和函数：

1≤[Tt]≤[Tr],t∈(0,1).

1≤[Tt]≤[Tr]+[Ts],s∈(0,1).

[Ts]+1≤[Tt]≤[Tr]+[Ts],s∈(0,1).

并据此构造下列两个比值型监测统计量：

Γ1(r)=

Γ2(r)=

定理1若假设(4)～(8)成立，则在原假设(2)下，当T→∞时有Γ1(r)⟹γ1(r)，

证明：设

(9)

若假设(4)～(8)成立，则在原假设(2)下，当T→∞时，由文献[10]中CUSQ渐近分布证得

(10)

(11)

由式(9)～(11)及连续映照定理得证定理1.

定理2若假设(4)～(8)成立，则在备择假设(3)下，当T→∞时有Γ1(r)→∞.

证明：由(7)及中心极限定理，得

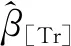
从而满足备择假设(3)时有

2[Tr]-1/2(β*-β0).

(β*-β0)2Op(1)>0

(12)

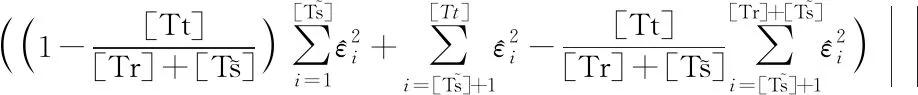
(β*-β0)2Op(1)>0

(13)

由式(9)、(10)、(12)、(13)得证定理2.

第二个监测统计量也有类似的结论.

定理3若假设(4)～(8)成立，则在原假设(2)下，当T→∞时有Γ2(r)⟹γ2(r)，

γ2(r)=

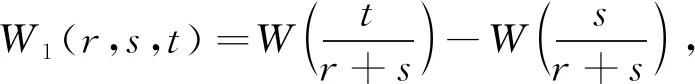
证明：同定理1的证明，

(14)

由式(9)、(10)、(14)及连续映照定理得证定理3.

定理4若假设(4)～(8)成立，则在备择假设(3)下，当T→∞时有Γ2(r)→∞.

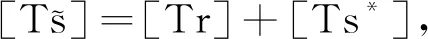
3 数值模拟

通过数值模拟检验方法的有限样本性质.表1列出了用10 000个标准正态分布的历史样本及历史样本量与监测样本量比值r取0.1,0.2,0.3,0.4,0.5时经1 000次循环得到的检验水平α=0.05的临界值.

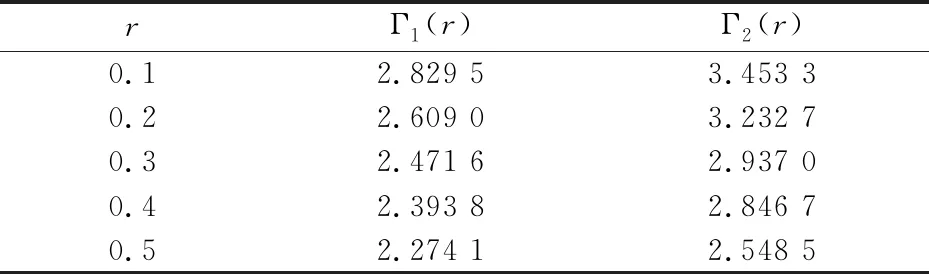
表1 两个监测统计量的临界值表

采用文献[11]的模型及假设β0i=0,β1i=0生成数据，历史样本量[Tr]取200，监测样本q分别取0.5-1[Tr],0.4-1[Tr],0.3-1[Tr],0.2-1[Tr],0.1-1[Tr]时，在α=0.05检验水平下做模拟.在表2中，经验水平随着r取值逐渐上升.固定r值时，历史样本量与监测样本量的比值较大于r时结果更趋近于检验水平.而该比值小于r时Γ1,2(r)经验水平渐失真，此时样本量相对较小，参数的估计残差平方和比值较不准确.

表2 两个监测统计量的经验水平(百分数)

由表3和表4比较参数变化时的检验势和平均运行长度，并判断是否快速监测到变点.显然，Γ1(r)比Γ2(r)监测变点时的power较高，且在部分情况下ARL较短.用不同r值的临界值监测时，不同位置的变点监测模拟结果power都较文献[13]更趋近于1.这表明去除了估计样本标准差产生的误差提高了监测精确度.同时在变点时刻靠后时，该方法仍能监测到变点，但ARL稍长.

表3 截距项在[Ts*]处由0变为1时的power与ARLs(百分数)

表4 斜率在[Ts*]处由0变为1.4时的power与ARLs(百分数)

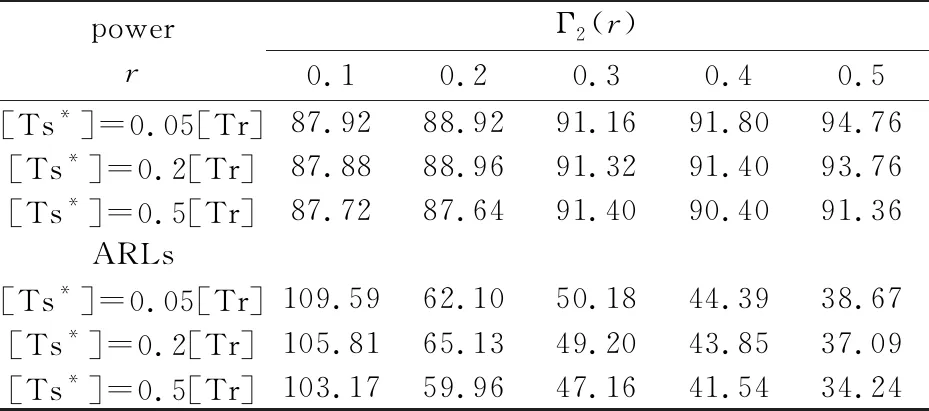
续表4

模拟结果表明,比值型监测统计量对检验势和监测结果的稳定性都有了较大改进，对监测变点时刻靠后情况的效果也有所改进.在实际数据监测时，由于无法判定可能出现变点的时期，可取r=0.1时的临界值监测，以便在监测较多样本量时控制好犯第一类错误,且尽可能的减小监测到变点的延迟时间.

4 实例

图1(a)给出2016年9月12日至2018年1月18日IBM股票收盘价格，图1(b)是其波动不均匀的一阶差分数据.取前200个样本为历史数据，在显著性水平α=0.05下，用文中监测统计量监测变点，Γ1(r),Γ2(r)均在[Ts*]=78处监测到变点.而用文献[13]的方法则监测不到变点，表明新方法能够尽快且准确监测到变点.

(a)收盘价格

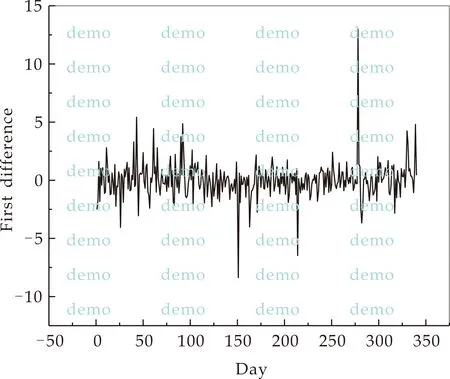
(b)一阶差分图1 IBM股票收盘价格及其一阶差分数据

5 结论

文章研究了线性回归模型系数变点的在线监测问题，在很多学者研究的基础上，提出了两个基于回归残差的平方累积和的比值型监测统计量，给出其极限分布与一致性的证明.通过数值模拟与实例分析，新的监测统计量有效提高了检验势与监测结果的稳定性，对变点出现时刻靠后情况的监测结果有所改进.但关于如何缩短监测的平均运行长度，仍需进一步研究.