基于广义Ⅱ型模糊聚类的图像分割算法

陈景文，徐 鑫，雷 涛，加小红，薛丁华

(1.陕西科技大学 电气与控制工程学院,陕西 西安 710021；2.陕西科技大学 电子信息与人工智能学院,陕西 西安 710021)

0 引言

图像分割是图像识别和计算机视觉的基础，是图像分析和图像理解的重要组成部分.图像分割实质上就是预测图像中每个像素所属的类别，目前多种图像分割方法已被提出，其中，模糊聚类是常用的一种图像分割算法[1].传统的模糊C均值聚类算法(Fuzzy C-Means，FCM)[2]是基于图像像素分类的分割方法，由于没有考虑图像的空间信息，导致分割结果对噪声特别敏感.

针对FCM算法的不足，许多的改进方法被提出，文献[3]提出了结合空间信息的模糊C均值聚类算法(Fuzzy C-Means Clustering with Spatial Constraints，FCM_S)，引入了空间邻域信息，虽然降低了对噪声的敏感性，但引入参数的选择对分割结果有很大的影响.文献[4]提出了鲁棒性的模糊局部C均值聚类算法(Fuzzy Local Information C-Means,FLICM),通过引入模糊因子，提高了抗噪性能，且该模糊因子没有任何参数选择，但该算法处理不确定性的能力较差，造成聚类中心的位置也不是很精确，最终影响图像的分割结果.

FCM算法以及这些改进方法都是以I型模糊集为基础，I型模糊集表达的是样本与每个聚类中心的隶属关系，其中的隶属度是确定的数值，导致I型模糊集描述不确定性的能力受到限制，并且在实际应用中图像本身存在多种不确定性[5-8].Ⅰ型模糊集为基础的FCM算法不能很好地处理图像中的这些不确定性问题，导致图像的分割结果差.

为了改善Ⅰ型模糊聚类处理图像不确定性的能力，引入Ⅱ型模糊集.Ⅱ型模糊集的概念是Zadeh[9]提出的，它是对Ⅰ型模糊集的扩展，Ⅱ型模糊集可以简单理解为对Ⅰ型隶属度函数取值进行模糊化，其隶属度值对应于一个Ⅰ型模糊集，从而使描述的集合的模糊性增强.也就是说，相比Ⅰ型模糊集，Ⅱ型模糊集通过增加描述与处理不确定性的维度，使得Ⅱ型模糊聚类算法具有更强处理图像不确定性的能力，进而可以相对完整地表达图像不确定性信息[10-15].

文献[16]提出了区间Ⅱ型模糊c均值聚类算法(Interval Type-2 Fuzzy C-Means，IT2 FCM)，采用两个模糊加权指数来构造区间二型模糊集的上、下主隶属度函数，而二级隶属度函数则釆用便于运算的区间Ⅱ型二级隶属度函数，即所有二级隶属度值为1.区间Ⅱ型模糊集是Ⅱ型模糊集的一种特殊形式，虽然它通过对二级隶属度函数作简化定义来减少Ⅱ型模糊集的运算复杂度，其处理不确定性的能力也有所提升，但是算法的鲁棒性较差，对图像的分割结果也不是很好.

文献[17]提出了广义Ⅱ型模糊C均值聚类算法(General Type-2 Fuzzy C-Means，GT2 FCM)，与IT2 FCM 算法选用两个模糊加权指数的方式不同，GT2 FCM算法选用完整的Ⅰ型模糊集的语言项对模糊指数m进行描述，即为语言模糊项参数.利用语言模糊项参数构造GT2模糊聚类隶属函数，再使用α平面表示方法，将输入不确定性转化为获取的聚类的不确定模糊位置，简化算法的复杂度.该算法拥有更强的描述不确定性因素的能力，但是由于未考虑图像的空间信息，导致分割结果对噪声较为敏感，使得分割出的区域不连续，图像分割结果较差.

针对广义Ⅱ型模糊C均值聚类算法没有考虑空间分布信息，导致算法鲁棒性不好和图像分割结果较差的问题，本文提出一种基于邻域信息的广义Ⅱ型模糊C均值聚类算法(General Type-2 Fuzzy C-Means Algorithm Based on Neighborhood Information，GT2 FCM_N).在广义Ⅱ型模糊C均值聚类算法的基础上引入模糊因子，以模糊的方式结合邻域的空间信息和灰度信息，自动地实现了图像细节和噪声的平衡，使得该算法在保证处理图像不确定性因素能力的同时，不仅增强了算法的鲁棒性，而且提高了图像分割结果的准确性，进而提升算法的性能.通过在合成图像和自然图像上进行实验对比，说明了改进方法的优越性，同时验证了该算法能有效抑制噪声的影响，从而实现图像的准确分割.

1 相关算法

1.1 GT2 FCM算法

在模糊聚类算法中，模糊加权指数m的取值直接影响数据聚类划分的位置和质量.然而，用精确的数值来表示输入数据的模糊性是很困难的.广义Ⅱ型模糊C均值算法(GT2 FCM)将Ⅱ型模糊集引入到模糊聚类中，通过α-plane表示方法来简化算法的复杂度[18-20].GT2 FCM算法是以T1模糊集的语言术语来表达模糊的概念，然后利用语言模糊项参数构造GT2模糊聚类隶属函数.使用α-plane表示，将输入不确定性转化为获取聚类的不确定模糊位置，具有处理图像数据的不确定性能力[17].

语言模糊项参数M可以用它的α-cuts来表示，如下所示

M=∪α∈[0,1]α/SM(α)

(1)

其中，

(2)

GT2 FCM算法的隶属度函数可由α-cuts表示为：

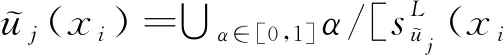
(3)

(4)

(5)

式(4)和式(5)中：dij表示xi与vj之间的欧氏距离，dil表示xi与vl之间的欧氏距离.

(6)

(7)

(8)

式(8)中：K是质心区域离散化步骤的个数，yi表示这些离散步骤的位置向量.GT2 FCM算法的示意图如图1所示.

图1 GT2 FCM算法的示意图

1.2 FLICM算法

Kinidis等[4]提出了一种鲁棒模糊局部信息C均值(FLICM)算法，以改善对噪声的敏感程度，保留图像细节.该算法将局部空间信息和灰度信息以一种新的模糊方式结合起来，称为模糊因子Gji，被定义为：

(9)

式(9)中：dir表示像素i和r之间的空间欧氏距离，ujr是第r个像素点属于第j个聚类中心的隶属度，m是每个模糊隶属度的加权指数，vj是聚类j中心的原型.

FLICM算法的目标函数定义为：

(10)

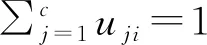
(11)

(12)

FLICM算法引入模糊因子，以模糊的方式将灰度信息和局部空间信息结合在一起，不仅增强了算法的抗噪性，而且较好的保持了图像的细节部分.该算法不含经验性调整的参数，通过模糊局部约束自动实现图像细节和噪声的平衡，同时提高聚类性能.但是该算法的聚类位置不是很精确，且处理图像不确定性因素的能力差.

FLICM算法的步骤如下：

步骤1：设定聚类个数c，模糊指数m和停止条件ε；

步骤2：随机初始化模糊隶属度矩阵；

步骤3：设置循环计数器b=0；

步骤4：使用式(11)计算聚类中心；

步骤5：使用式(12)计算隶属度；

步骤6：若{∪(b)-∪(b+1)}<ε，停止迭代，否则b=b+1，返回步骤4继续运行.

2 本文算法

GT2 FCM算法是以Ⅱ型模糊集为基础，聚类位置较为准确，处理不确定性的能力高于Ⅰ型模糊集，但没有采用数据的空间分布信息，导致算法的鲁棒性不是很好，难以对图像进行准确分割.FLICM算法中的模糊因子以一种模糊的方式将空间和灰度信息结合起来，提供了抗噪性能，且没有任何参数选择，然而该算法属于Ⅰ型模糊聚类算法，聚类位置不是很精确，处理数据以及算法的不确定性的能力差.为了提高算法的鲁棒性和图像分割准确性，同时确保处理不确定性的能力，本文提出了一种基于邻域信息的广义Ⅱ型模糊C均值聚类算法.该算法在GT2 FCM算法的基础上引入模糊因子，其定义如式(9).

模糊因子没有使用任何控制图像噪声和图像细节之间平衡的参数，可以自动实现它们之间的平衡.其以模糊的方式结合了邻域空间信息和灰度信息，提升了算法对噪声的不敏感性.根据中心像素与邻域像素的欧式距离来控制邻域像素对中心像素的影响.使用原始图像的信息，避免可能导致细节丢失的预处理步骤，使得图像细节能够保留.

本文提出算法的目标函数为

(13)

式(13)中：c为聚类个数，n为图像像素个数，Gji为模糊因子，M为语言模糊项.

(1)构造GT2模糊隶属函数

语言模糊项参数M可以用它的α-cuts来表示，如公式(1)和公式(2).本文选用高斯函数作为语言模糊项参数M来表达模糊性.

GT2 FCM_N的隶属度函数使用其α-cuts表示为

(14)

GT2 FCM_N隶属度函数的α-plane表示为

uj(α)=∑xi∈XSuj(xi│α)

(15)

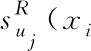
(16)

(17)

所以，使用语言模糊指数M的α-cuts构造α-planes的带有模糊因子的GT2聚类隶属度函数uj，从而增强模糊系统方法的模糊性来提高处理不确定性因素的能力，改善图像噪声及异常点的影响.

(2)聚类位置更新

FCM算法的聚类中心位置更新基于隶属度矩阵U确定新的聚类位置.在GT2 FCM_N算法的情况下，所提出的聚类位置更新方法包括首先将GT2模糊聚类隶属类型减少到它们的T1模糊质心中，然后将这些质心去模糊化到精确的聚类位置.

质心Cuj表示为

(18)

通过对聚类质心Cuj的去模糊化，计算出精确的聚类中心

(19)

式(19)中：T是质心区域离散化步骤的个数，T的值直接由所使用的α-plane个数决定.

本文提出的GT2 FCM_N算法的步骤如下：

步骤5：使用式(18)进行类型约简；

步骤6：使用式(19)更新聚类中心；

步骤7：若{V(b)-V(b+1)}<ε，停止迭代，否则，返回步骤3继续运行.

基于邻域信息的广义Ⅱ型模糊C均值聚类算法，通过引入的模糊因子可以自动确定空间和灰度的关系，没有任何的参数选择；且改善了对噪声的敏感性，鲁棒性好；同时具有更强的处理不确定性的能力；能够保留图像细节信息的能力，进而提高了图像分割的准确性.

3 实验结果与分析

在本节中，为验证本文算法的有效性，主要通过对合成图像和自然图像进行实验测试，并将4种聚类算法:FCM、FLICM、IT2 FCM和GT2 FCM与本文算法GT2 FCM_N进行了对比，对噪声的鲁棒性和图像分割的准确性进行了分析.实验环境为：CPU为Intel(R)Core(TM)i7-6700 @ 3.40GHz,RAM为4G，运行环境为Win 7，编程环境为Matlab 2017b.

3.1 合成图像

实验采用了两张尺寸为256×256的合成图像.第一张合成图像是4类，第二张合成图像是3类，如图2(a)和3(a)所示.分别对这两张合成图像进行高斯滤波、椒盐滤波和均匀噪声滤波，并利用这些滤波后的图像对上述算法的有效性和鲁棒性进行了测试.图2(c)～(g)和图3(c)～(g)显示了不同算法的分割结果.

在图2中，FCM、IT2 FCM和GT2 FCM算法都对高斯噪声敏感，图像分割结果都比较差，而GT2 FCM算法分割结果略好于FCM和IT2 FCM.FLICM算法由于引入了空间邻域信息对高斯噪声有较好的鲁棒性，图像分割结果优于FCM、IT2 FCM和GT2 FCM.从图2(g)可以看出，与其它算法相比，本文提出的GT2 FCM_N分割结果更为理想.

(a)原图 (b)噪声图

(c)FCM (d)FLICM

(e)IT2FCM (f)GT2FCM

(g)GT2FCM_N图2 第一张合成图像的分割结果对比(高斯噪声:均值为0，方差15%)

从图3可以看出，FCM、IT2 FCM和GT2 FCM算法的图像分割结果接近，FLICM对椒盐噪声敏感，它们的视觉效果都比较差.GT2 FCM_N算法由于引入了广义Ⅱ型模糊集和空间邻域信息，提高了抗噪性能，其分割效果优于其它算法.

(a)原图 (b)噪声图

(c)FCM (d)FLICM

(e)IT2FCM (f)GT2FCM

(g)GT2FCM_N图3 第二张合成图像的分割结果对比(椒盐噪声的强度为5%)

为了评估不同算法对噪声图像的性能，本实验选取三类噪声：高斯噪声、椒盐噪声和均匀噪声去污染合成图像，采用两个性能指标，分割精度(segmentation accuracy,SA)和量化指数(comparison scores,CS)测试各类算法的分割效果.SA定义为正确分类的像素之和除以像素总数之和，CS定义为像素集Ak与标准值Ck的相等程度，公式如下

(20)

(21)

式(20)和式(21)中：c表示聚类个数，Ak表示聚类结果中属于第k类的像素集合，Ck表示标准分割结果(Ground truth,GT)中属于第k类的像素集合，SA和CS的值越大，表明算法的聚类效果越理想.所有算法在不同种类和不同水平的噪声干扰下对合成图像进行处理，表1和表2给出了五种算法的平均分割精度和量化指数的实验结果.

表1 五种算法在第一张不同噪声强度合成图像的分割精度(SA%)对比

表2 五种算法在第二张不同噪声强度合成图像的量化指数(CS%)对比

从表1和表2可以看出，对于含有不同种类和水平噪声的合成图像，GT2 FCM_N的分割精度始终高于其他算法.与其他算法相比，GT2 FCM_N对不同噪声的鲁棒性明显更好.FCM、IT2 FCM和GT2 FCM对椒盐噪声及高斯噪声都很敏感，因此SA和CS的值都较低.FLICM对高斯噪声的鲁棒性较好，而对椒盐噪声和均匀噪声较为敏感.

通过分析合成图像的分割结果和指标可得，不同算法对不同类型噪声的鲁棒性不同，相比FCM、FLICM、IT2 FCM和GT2 FCM这四种算法，本文GT2 FCM_N算法的分割效果更为理想，对噪声的鲁棒性明显提高.

3.2 自然图像

为了验证本文算法对自然图像的分割效果，本实验选取Berkeley Segmentation Dataset (BSDS500)(图像尺寸大小为481×321或321×481)彩色图像，每幅图像都有对应的GT(Ground truth)分割结果.采用FCM、FLICM、IT2 FCM、GT2 FCM这四种算法与本文GT2 FCM_N算法进行实验对比，在BSDS500的数据集上实现了这些算法，图4和图5为部分图像分割结果.

从图4和图5中可以看出，由于FCM算法对像素的不均匀分布较为敏感，图像分割结果不是很好.GT2 FCM算法和IT2 FCM算法的图像分割结果也不是很好，和FCM分割结果相近.FLICM由于引入了邻域信息，图像分割结果有了改善，比FCM、IT2 FCM和GT2 FCM好.从图4(f)和图5(f)可得，不同图像的分割结果具有准确的轮廓，使用GT2 FCM_N可以得到良好的目标分割结果.通过对比图4(b)～(f)和图5(b)～(f)可得，GT2 FCM_N的分割结果最为理想.所以，本文所提出的GT2 FCM_N算法为自然图像提供了很好的分割效果.

(a)原图 (b)FCM (c)FLICM (d)IT2FCM (e)GT2FCM (f)GT2FCM_N图4 五种算法对自然图像的分割结果比较

(a)原图 (b)FCM (c)FLICM (d)IT2FCM (e)GT2FCM (f)GT2FCM_N图5 五种算法对自然图像的分割结果比较

为了进一步分析评价这些算法的分割效果，利用概率边缘指数[25](probabilistic rand index,PRI)、重叠比率[26](Covering,CV)、变化信息[27](variation of information,VI)、全局一致性误差[28](global consistency error,GCE)、边界位移误差[29](boundary displacement error,BDE)作为性能指标对分割结果进行测试.其中，PRI是一种相似性度量，度量实际分割结果与GT之间标签一致的像素对的比例.CV是度量实际分割结果与GT之间区域的重叠比率.VI是度量两个聚类结果之间的平均条件熵距离.GCE是度量实际分割结果与GT之间相互一致的全局误差.BDE是一种误差测量方法，用于测量实际分割结果与GT之间边界像素的平均位移误差.当实际分割结果接近GT，对应的PRI和CV较大，GCE、BDE和VI较小.

利用上述指标测试这些算法在BSDS500图库上的平均分割结果，选择了最佳聚类个数c，不同算法的PRI、VI、CV和BDE的平均值如表3所示.

表3 五种算法在BSDS500的图库的测试结果

在表3中，FCM、FLICM、IT2FCM、GT2FCM得到了相似的PRI、CV、VI、GCE、BDE值，说明这些算法在实际图像分割中具有相似的性能.本文GT2FCM_N算法在PRI、VI、CV、GCE和BDE值上优于其他算法，说明GT2FCM_N能够获得较好的分割结果.

综上所述，本文所提出的GT2FCM_N算法不仅鲁棒性好，而且能够为不同类型的图像提供良好的分割结果.

4 结论

为了提高广义Ⅱ型模糊C均值聚类算法的鲁棒性和图像分割准确性，本文提出了一种基于邻域信息的广义Ⅱ型模糊C均值聚类算法.该算法由于引入模糊因子，没有任何参数选择，在图像分割时，能更好地保留图像细节信息，有效地改善对噪声敏感的问题.实验结果表明，本文提出的基于邻域信息的广义Ⅱ型模糊C均值聚类算法不仅有效地增强了鲁棒性，同时保证了聚类算法处理参数不确定性的能力，因此能实现准确的图像分割结果.但是，该算法的运算复杂度较高，如何优化Ⅱ型模糊集的运算方法，仍需进一步深入研究.