颗粒增强金属基复合材料参数化建模研究

2020-01-06信振洋王悦苗文成陈华辉

矿业科学学报 2020年1期

信振洋，王悦，苗文成，陈华辉

中国矿业大学(北京) 机电与信息工程学院，北京 100083

颗粒增强金属基复合材料一般由颗粒相、基体相和界面相3部分组成，力学性能良好，在航空航天、车辆、矿用设备等领域有着广泛的应用。随着计算机技术的发展，以有限元为代表的数值模拟方法逐步成为研究复合材料力学性能的有力工具。颗粒增强复合材料具有较为复杂的细观结构[1]，主要体现在颗粒的随机分布和颗粒形状不规则两个方面，导致其几何模型的构建成为难点。目前颗粒增强复合材料细观模型主要有2大类：单胞模型(Unit Cell，UC)和代表性体积单元模型(Representative Volume Element，RVE)。单胞模型是将增强体视为规则排布，从而将整个复合材料简化为只含有一个或者若干个颗粒的最小单元[2-3]；代表性体积单元模型的增强颗粒数量较多，从几个到几百个不等，随机分布更接近复合材料的实际结构[4]。

增强颗粒常见有球状和不规则状等，相关研究表明，颗粒形貌越接近实际，模拟结果与实验值的误差则越小[5-6]。球状颗粒形貌较为简单，可直接采用球状模型建模；不规则颗粒的建模相对较为复杂，为使颗粒模型接近实际不规则颗粒，采用基于真实细观形貌的三维重构方法构建颗粒模型，通过CT扫描或逐层研磨的方式获得分层照片，并进一步合成为三维几何模型[8-10]。这类方法获得的RVE模型最接近实际的细观结构形貌，但实施限制较多，成本高，工作量大。为构建接近实际的颗粒模型并且避免三维重构方法的不足，采用程序语言构建随机凸多面体的方法生成接近实际颗粒的RVE模型[12-14]。建模属于颗粒增强复合材料力学性能有限元仿真的前处理过程，但是目前建模过程与有限元仿真软件的集成度并不高，一般需要先用建模软件生成模型，之后导入有限元软件计算。这无疑降低了整个仿真流程的效率，容易出现几何模型与有限元软件的兼容性问题。因此，有必要将建模算法通过程序语言集成到有限元仿真软件中，构建更加高效用户界面，实现复合材料建模与有限元计算的无缝连接。

多颗粒随机分布代表性体积单元模型的构建可采用随机顺序吸附算法和扰动算法等。随机顺序吸附算法是通过向RVE所占据的几何空间中逐一投放颗粒，并判断当前颗粒是否与已存在颗粒之间发生干涉，如不干涉则保存当前颗粒的相关数据，投放终止条件是达到体积分数要求或循环次数达到最大设定值[4，15]；扰动算法是首先赋予所有颗粒规则的分布位置，然后对每个颗粒施加随机距离的扰动量，当所有颗粒满足无干涉随机分布之后保存位置信息[16]。基于随机顺序吸附算法采用Python语言，在ABAQUS软件中实现了颗粒增强复合材料几何模型的参数化建模，并封装为插件(CUMTB RVE Modeling Tool)，该套插件扩展了有限元软件ABAQUS的功能，程序可移植性强，能有效地降低复合材料仿真的建模难度，提高工作效率。

复合材料力学性能有限元仿真的基本作用之一是对其力学性能进行预测，通过模拟的结果指导复合材料的设计。通过粉末烧结方法制备的ZTAp/Fe45复合材料，具有高硬度和高耐磨性，是一类新型的耐磨复合材料，有望应用于煤矿刮板输送机和破碎机等设备中，可有效提高相关零部件的耐磨性，降低设备损耗。笔者采用有限元仿真方法分析了ZTA增强颗粒的形状、体积分数、界面性能等因素对ZTAp/Fe45复合材料弹性模量的影响，并与实验结果进行对比。仿真结果表明，不规则状颗粒对ZTAp/Fe45复合材料弹性模量的增强效果高于球状颗粒，颗粒体积分数的增加和界面弹性模量的提升均能提高复合材料的弹性模量。

1 ABAQUS-Python二次开发原理

作为商用非线性有限元分析软件的代表，ABAQUS提供了丰富的程序语言接口，如Python、C/C++、FORTRAN等，以方便用户通过二次开发实现特有的功能。前处理过程多采用Python语言，而FORTRAN和C/C++可用来开发用户子程序，如自定义材料子程序UMAT/VUMAT以及用户单元子程序UEL/VUEL等，这些功能扩展增加了ABAQUS软件的灵活性。

ABAQUS软件与Python语言的用户接口如图1所示，可使用用户图形界面(Graphical User Interface，GUI)、命令行或者脚本文件3种方式向ABAQUS自带的Python解释器输入命令，进一步生成input文件提交内核运算。对于简单的代码或者不需要大量反复使用的代码，可采用命令行或脚本文件输入，但对于需要反复使用或者变量较多的程序，这2种方式操作复杂易出错。而采用GUI界面输入的方式则可以降低操作错误发生的概率，用户不需要关注内部的运行代码，只需要关注操作界面中参数的输入或者选取。本文采用自定义GUI插件的方式实现了ABAQUS软件中的颗粒增强复合材料的参数化建模。

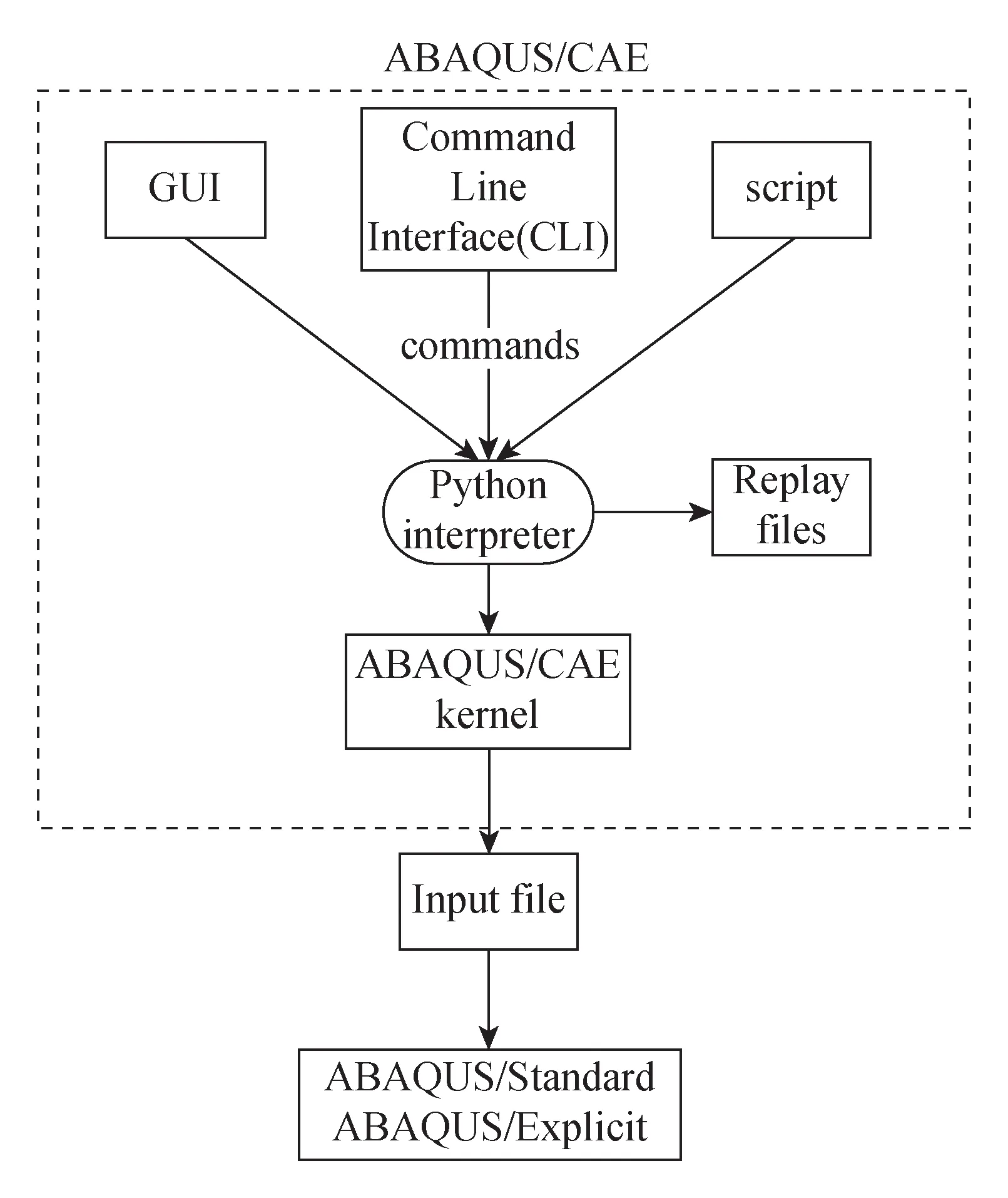
图1 Python语言与ABAQUS/CAE接口Fig.1 Interface of Python and ABAQUS/CAE

2 参数化建模的实现

2.1 单胞模型

颗粒增强复合材料细观结构的复杂性决定了采用参数化建模的必要性。参数化建模是指通过输入复合材料的特征参数，如颗粒形状、尺寸、体积分数、分布方式以及模型尺寸等数据，构建颗粒增强复合材料几何模型。这一建模过程需要借助程序语言来实现。

为了实现参数化建模，针对不同类型的计算模型编写相应的Python语言程序，并将构建不同几何模型的程序封装成相应的插件(CUMTB RVE Modeling Tool)，该插件由3个模块组成，可用来构建轴对称单胞(Part-1)、三维周期单胞(Part-2)和三维或二维的随机分布代表性体积单元(Part-3)的模型。在该插件中，通过直接在用户界面输入相关参数，如模型的名称、体积分数、颗粒半径以及点选颗粒形状参数，可实现在ABAQUS软件中生成对应的复合材料几何模型，从而实现参数化建模。

轴对称单胞[17-20]和三维周期单胞[21-23]是基于颗粒规则分布的假设，并将复合材料简化为最小结构单元的建模方式，这2类模型的特点是计算规模小、效率高，但由于对复合材料的结构简化较多，不能体现随机分布的特征，有一定局限性。轴对称单胞建模插件界面如图2所示。此类单胞中颗粒模型常见的有切边圆柱状、圆柱状和球状3种。在轴对称单胞中，球状颗粒模型用来模拟实际颗粒形状为球状的颗粒；多面体状颗粒由于不能用回转体来表征多面体结构，而采用柱状和切边圆柱表征颗粒的棱边和尖角。

图2 轴对称单胞建模插件界面Fig.2 Plug-in GUI of the axisymmetric unit cell model

根据不同的单胞选取规则[23]，三维单胞可简化为简单立方(SC)、体心立方(BCC)、面心立方(FCC)、密排六方(HCP)等，为了能够施加相对简单的周期性边界条件，一般选用立方体形状的单胞[3，22，25]。如图3所示，仅对常用的简单立方、体心立方、面心立方3种单胞模型进行编程和插件封装。

图3 三维立方单胞建模插件界面Fig.3 Plug-in GUI of the 3D unit cell model

2.2 随机分布代表性体积单元模型

不规则多面体颗粒的形状具有较强的随机性，为了降低建模难度，在具体的建模算法中将此类颗粒视为随机凸多面体，其截面形状为凸多边形。对于二维模型，采用颗粒平均尺寸所确定的圆作为控制条件，随机生成位于圆上的若干点，按逆时针方向(或顺时针方向)顺次连接各个顶点，即可生成内接于圆的不规则凸多边形，多边形的边数被设定为3 ～ 6个。图4为生成的某个随机四边形示意图。

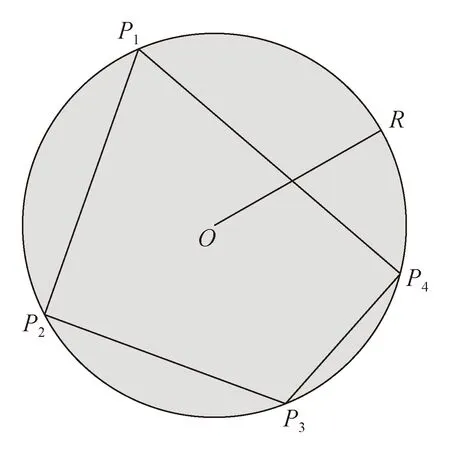
图4 随机多边形示意图Fig.4 Schematic diagram of a random polygon

随机凸多面体的生成可通过球体或者规则凸多面体空间拓展[26-27]以及二维平面图形拉伸[28]等方法实现。本程序中采用了二维平面图形拉伸方法得到三维颗粒模型，颗粒构建如图5所示。

首先在XOY平面内构建形状随机的三角形或四边形，然后在Z轴方向拉伸一定厚度得到凸多面体，再对所得凸多面体进行倒角处理得到所需的随机形貌的凸多面体。图5中颗粒的长轴和短轴分别为l0和b0，其比值l0/b0、l1/l0和b1/b0为变形系数，在长短轴确定的情况下变形系数为0 ～ 0.5的随机数。二维截面构建完成后，在垂直纸面的法向拉伸一个等于短轴长度b0的厚度，从而得到三维颗粒模型，短轴长度b0等于颗粒的平均尺寸。根据对一定数量的ZTA颗粒形貌尺寸的统计，其颗粒的长短轴比值为1 ～ 1.5，因此建模过程中l0/b0为1 ～ 1.5的随机数。

颗粒的随机分布采用随机顺序吸附算法实现[4，29-30]，该算法的基本流程如图6所示。

颗粒的无干涉随机分布是构建随机分布代表性体积元的关键，球状和圆形的颗粒干涉采用球心距离判断，而凸多面体和凸多边形可根据体积或面积判断。例如，某多面体一个顶点侵入到另一个多面体内部时，可用该点与被侵入的多面体各个面所组成的多面体体积之和与被侵入多面体体积相比较即可判断。颗粒随机分布建模插件操作界面如图7所示，通过该插件可构建圆形或随机凸多边形颗粒的二维RVE和球状或随机凸多面体颗粒的三维RVE。

图7 随机分布代表性体积单元插件界面Fig.7 Plug-in GUI of RVEs

3 ZTAp/Fe45复合材料力学性能分析

图8所示为实验制备的纯Fe45和ZTAp/Fe45复合材料拉伸试样。ZTAp/Fe45试样的ZTA颗粒体积分数φ(ZTA)为20%，形状为不规则形貌，颗粒平均尺寸为2 mm，颗粒形貌如图9所示。采用的实验设备为WDW-200微机控制电子式万能实验机，拉伸速度为1 mm/min。

图8 纯Fe45与ZTAp/Fe45拉伸试样Fig.8 Tensile specimens of pure Fe45 and ZTAp/Fe45

图9 不规则ZTA增强颗粒形貌Fig.9 Irregular morphological of ZTA particles

通过单轴拉伸实验测得该批次试样中基体材料Fe45平均弹性模量为187.7 GPa，泊松比为0.3；20%体积分数的ZTAp/Fe45弹性模量为210.7 GPa。

3.1 颗粒形状对ZTAp/Fe45力学性能的影响

ZTA增强颗粒通常有不规则状和球状2种形状。ZTA增强颗粒体积分数φ(ZTA)为20%的2种RVE模型如图10所示，颗粒平均尺寸为2 mm，代表性体积单元在X、Y、Z的3个方向尺寸均为8 mm。为了降低模型随机性所引起的误差，2种模型分别构建10个，共20个代表性体积单元模型，计算每种模型弹性模量的平均值。有限元计算模型中ZTA颗粒弹性模量为338.0 GPa，抗拉强度为344 MPa，泊松比为0.23[31]。

图10 ZTAp/Fe45代表性体积单元Fig.10 RVEs of ZTAp/Fe45

上述计算模型的有限元网格剖分示意图和边界条件如图11所示，网格控制尺寸为0.3 mm，采用C3D4四面体单元，模型的网格数量在10×104～16×104个，代表性体积单元网格数量的差异与颗粒形状和分布有关。颗粒网格与基体网格之间采用共节点的方式连接，即理想结合。模型边界条件为左侧面固定，右侧面与参考点耦合，对参考点施加应变量为0.3%的X轴正方向微小位移荷载，采用ABAQUS/Standard隐式求解器进行计算。

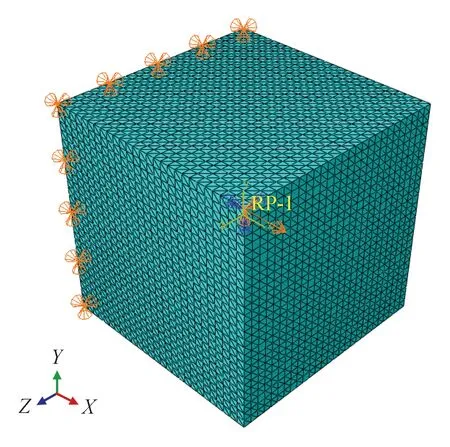
图11 代表性体积单元网格与边界条件Fig.11 RVEs meshes and boundary conditions

不规则多面体颗粒代表性体积单元和球状颗粒代表性体积单元计算得到的平均弹性模量分别为213.1 GPa和203.8 GPa，不规则多面体代表性体积单元所得结果与实验值210.7 GPa更为接近，但仍然高于实验值。产生这种误差的主要原因在于模型采用理想结合界面提高了基体与颗粒之间的载荷传递能力，导致计算结果相对实验值偏大。造成2种RVE模型弹性模量结果差异的主要原因在于颗粒形状对复合材料内部细观应力应变场影响不同。应变量为0.09%时ZTAp/Fe45的增强体Mises应力云图如图12所示。

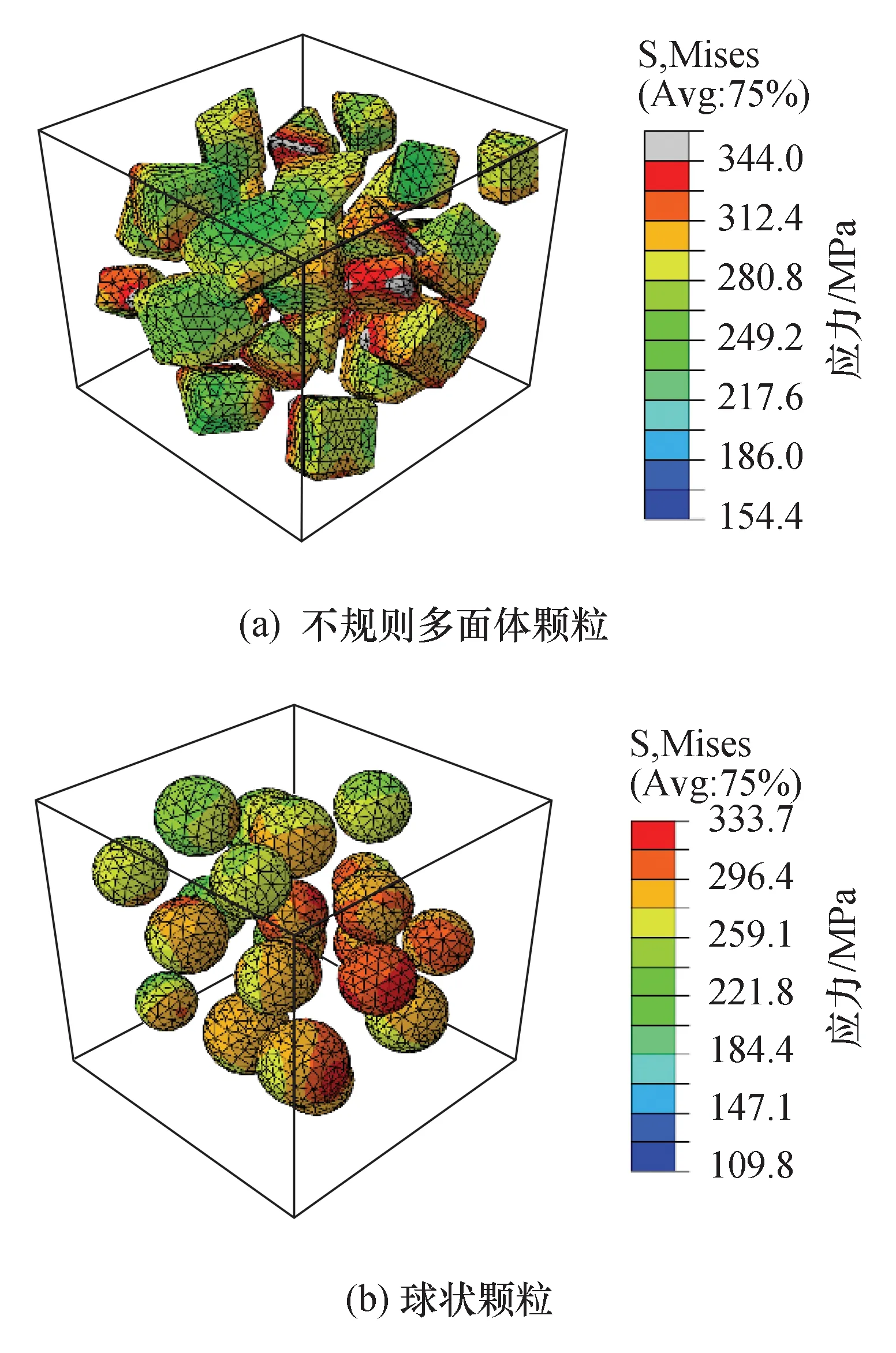
图12 ZTAp/Fe45的增强体Mises应力云图[φ(ZTA)为20%，应变量为0.09%]Fig.12 Mises stress nephogram of ZTA particles in ZTAp/Fe45 [φ(ZTA)=20%，strain=0.09%]

在应变量相同的情况下，不规则多面体颗粒高应力区域大于球状颗粒模型，承受的荷载更大，在颗粒的尖角和棱边附近由于应力集中现象出现明显的高应力区，图12(a)应力云图中高于ZTA抗拉强度(344 MPa)的灰色部分出现在该区域。随着形变量的持续增大，这些灰色区域将成为颗粒损伤的萌生区域；在相同应变量的情况下，图12(b)中的球状颗粒并未出现高于344 MPa的区域，最高应力值相对于不规则颗粒降低约50 MPa，说明在承受相同应变量时，不规则颗粒更易发生损伤。

图13为代表性体积单元与X轴平行截面的Mises应力云图。由图13可知，对于2种颗粒代表性体积单元模型，复合材料的高应力区域均出现在增强颗粒中，基体所承受的应力明显低于颗粒，说明ZTAp/Fe45复合材料在形变过程中增强颗粒表现出较好的承载能力。

图13 ZTAp/Fe45截面Mises应力云图(应变量为0.09%)Fig.13 Mises stress nephogram section of ZTAp/Fe45 (strain=0.09%)

3.2 ZTA颗粒体积分数对复合材料力学性能的影响

为分析ZTA颗粒体积分数对复合材料力学性能的影响，构建体积分数分别为5%、10%和15%的ZTAp/Fe45复合材料RVE模型，颗粒形状分别采用不规则多面体和球状，2种形状的颗粒均构建10个随机分布的代表性体积单元，总共60个模型，示例模型如图14所示。

φa(ZTA)—不规则颗粒体积分数；φb(ZTA)—球状颗粒体积分数图14 不同体积分数代表性体积单元模型Fig.14 RVEs with different volume fractions

在不同体积分数情况下，不规则颗粒RVE弹性模量计算结果均高于球状颗粒RVE计算结果，如图15所示。但是由于模型中颗粒形状以及分布方式的随机性，导致相同体积分数的模型计算结果亦会出现一定偏差。对于相同类型的颗粒来说，随着体积分数的增加会引起复合材料弹性模量的提升。

图15 颗粒体积分数与复合材料弹性模量曲线Fig.15 Volume fraction and elastic modulus curve of composites

体积分数为10%的增强体在应变量0.09%时的应力云图如图16所示。对比图12可知，在相同的应变量下，φ(ZTA)为10%的ZTAp/Fe45中颗粒所承受的应力相对低于φ(ZTA)为20%的ZTAp/Fe45，说明在较高体积分数模型中颗粒所承受的应力更大。这主要是由于高体积分数的情况下，颗粒间距更近，更易形成应力集中区域，同时也意味着在形变过程中颗粒更易发生破坏。

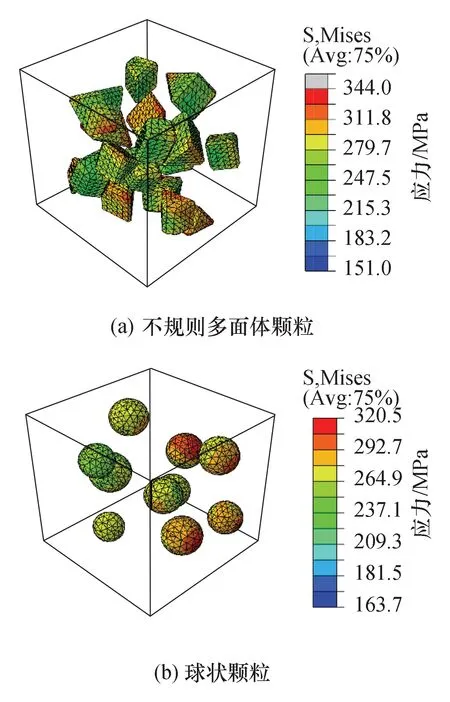
图 16 ZTAp/Fe45复合材料增强体Mises应力云图(φ(ZTA)=10%，应变量为0.09%)Fig.16 Mises stress nephogram of ZTA particles in ZTAp/Fe45 (φ(ZTA)=10%，strain=0.09%)

3.3 界面性质对ZTAp/Fe45力学性能的影响

在复合材料形变过程中，界面的力学性能对基体和增强体之间的荷载传递起关键作用，并通过这种方式对复合材料宏观力学性能产生影响。界面力学性能的模拟可采用黏聚力模型(Cohesive Zone Model，CZM)[21]和XFEM[32-33]等方法；另外，在小变形的情况下亦可采用线弹性力学模型近似表征界面的弹性力学性能[34]。本文采用线弹性力学模型分析小变形情况下界面弹性模量对复合材料弹性模量的影响。有限元模型中颗粒和基体采用C3D4单元进行网格剖分，界面单元采用C3D6三棱柱实体单元。界面单元的插入采用基于Python语言开发的内部程序iCoh实现，模型中界面单元的法向厚度设定为10 μm，其界面单元示意如图17所示。

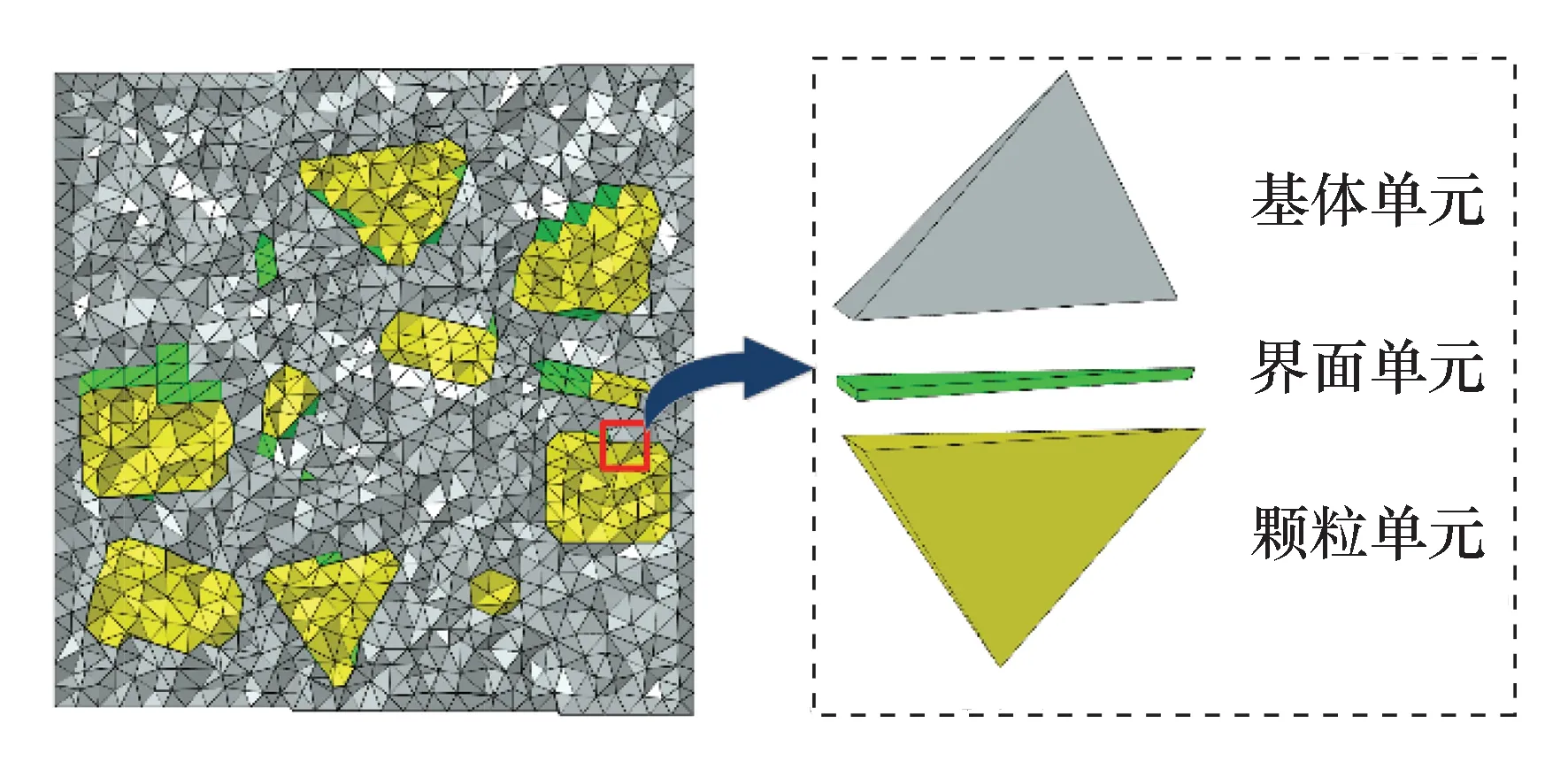
图17 界面单元示意图Fig.17 Interface element diagram

由于界面性能的测定较为困难，因此通过对界面设定一系列弹性模量值研究界面弹性模量对复合材料弹性模量的影响，界面的泊松比假定与基体材料泊松比一致。图18为体积分数20%的ZTAp/Fe45复合材料采用不同弹性模量的界面所得的弹性模量曲线。

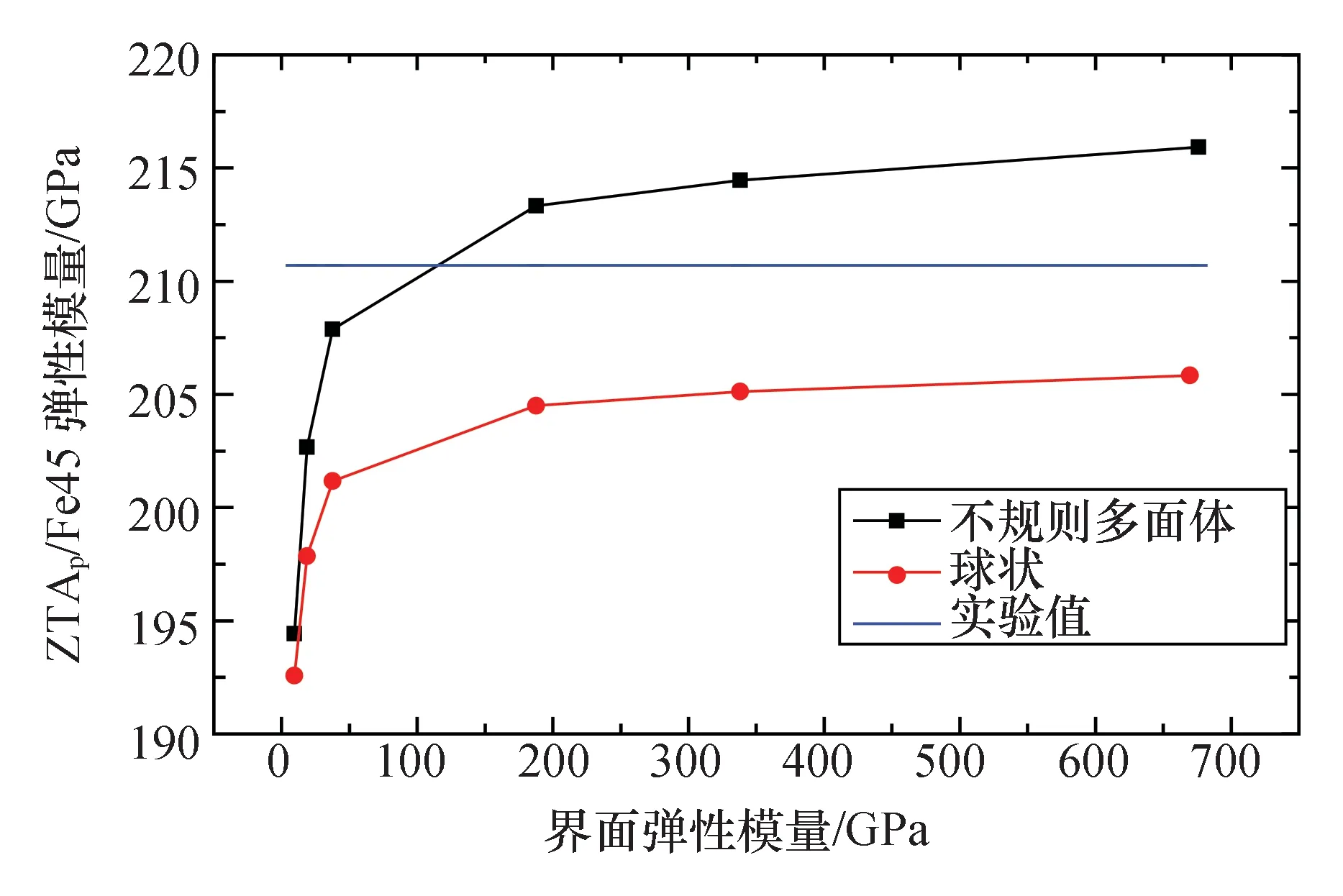
图18 界面弹性模量与ZTAp/Fe45弹性模量曲线Fig.18 Interface Young’s modulus and Young’s modulus curve of ZTAp/Fe45

由图18可知，在界面弹性模量低于基体弹性模量(187.7 GPa)的情况下，界面模量的增加使复合材料弹性模量提升明显；当界面模量在187.7～ 676.0 GPa(2倍的增强体弹性模量)时，复合材料弹性模量增长趋缓，此时界面模量的增加并不能显著提升复合材料的弹性模量。

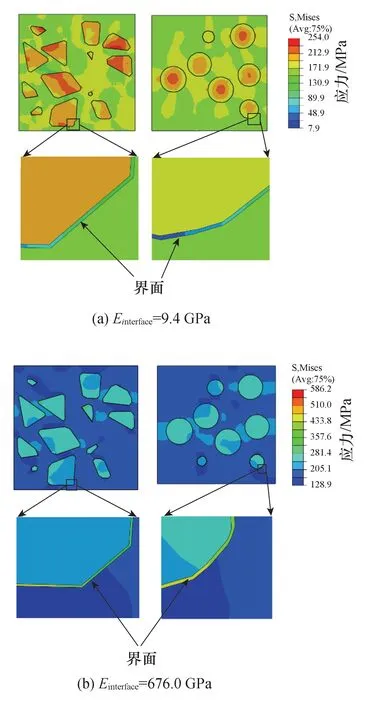
图19 ZTAp/Fe45复合材料应力云图截面(应变量为0.09%)Fig.19 Mises stress nephogram section of ZTAp/Fe45 (strain=0.09%)

图19所示为界面模量为9.4 GPa(基体弹性模量的1/20)和676.0 GPa情况下复合材料的应力云图，应变量均为0.09%。图19(a)中，界面区域为明显低应力区，对荷载的传递能力较弱，此时通过提升界面的弹性模量可以改善其传递荷载的能力，提高复合材料弹性模量；图19(b)中，界面区域为复合材料的高应力区，表现出较强的承载能力，而作为复合材料主体的基体相和颗粒相则表现出相对低的应力。根据复合材料细观力学均匀化理论[35]，虽然界面相为高应力区，但由于界面相在复合材料中占据的体积分数权重较小，此时复合材料弹性模量的主导因素转化为占更大体积分数权重的基体相和颗粒相。因此，在图18曲线中出现当界面弹性模量达到基体弹性模量之后复合材料弹性模量提升不明显的现象。