基于小信号模型的级联式单相VIENNA开关变换器的控制与仿真设计
2020-01-06王聪胡昊雨程红
王聪,胡昊雨,程红
中国矿业大学(北京) 机电与信息工程学院,北京 100083
煤矿主通风机是重要的安全设备,在煤矿生产成本中占比较高[1-2]。根据实际情况控制通风机的送风量,在保证安全送风的前提下,采用高压变频器调节通风机的转速可以有效地降低能源消耗和生产成本[3-4],但传统矿用高压变频器输入侧需要接入昂贵而笨重的工频变压器。由于矿用通风机并不需要反馈电能,因此研究一种能量单方向传输的矿用无工频变压器高压变频器对于进一步节约成本、降低能耗具有重要的意义[5-6],高压整流电路是矿用无工频变压器高压变频器的重要组成部分[7]。
VIENNA电路是由Kolar J W和Zach F C提出的一种能量单方向传输的整流电路[8]。VIENNA电路仅含有一个开关器件,但具有三电平结构,该开关器件所承受的电压仅为输出电压的1/2,近年来,VIENNA电路由于上述特点受到密切关注并广泛应用于功率因数校正(PFC)领域[9-10]。在高压大功率应用场合中,可以将多个单相VIENNA开关变换器级联,组成级联式单相VIENNA开关变换器。级联式开关变换器可以承受的电压随着级联个数的增加而成倍增加,电平数量也相应增加,交流侧电流谐波含量则相应减小[11-12]。研究这种级联式开关变换器有2个关键点,即实现单位功率因数整流和输出电压平衡。为了对2个关键点进行深入的理论和控制研究,需对级联式单相VIENNA开关变换器建立小信号模型[13]。大量文献对VIENNA电路进行了小信号建模研究[14-18],其中文献[14-16]采用状态空间平均法,对三相VIENNA功率因数校正电路进行了小信号建模;文献[18]参考峰值电流控制模式,对单相VIENNA开关变换器进行了小信号建模。但上述文献仅对传统单相或者三相VIENNA电路进行小信号建模研究,目前鲜有相关文献针对级联式单相VIENNA开关变换器进行小信号建模。
笔者对级联式单相VIENNA开关变换器进行小信号建模,推导相关传递函数表达式,根据该传递函数设计出合理的电压环和电流环补偿网络并进行Bode图分析;在Matlab/Simulink平台上搭建3个级联式单相VIENNA开关变换器,并通过星形连接组成的三相整流系统的仿真研究验证小信号模型的正确性。
1 拓扑结构及原理
1.1 无工频变压器高压变频器整流级原理及其优势
如图1所示,矿用无工频变压器高压变频器由三相高压整流级、高频DC-DC和三相逆变电路组成。其中,三相高压整流级是由3个级联式单相VIENNA开关变换器星接组成。通过增加每个级联式单相VIENNA开关变换器中单相VIENNA级联的数量,可以提高变频器的输入电压等级。因此,三相高压整流级输入侧可以与三相高压交流输入直接相连,无需工频变压器,高频DC-DC起到电气隔离的作用。

图1 矿用无工频变压器高压变频器Fig.1 Mining transformerless high-voltage AC driver
在实际系统应用中,以矿井典型电压1 140 V为例,1 140 V为交流输入线电压有效值,其中的某一相相电压的峰值为930 V,对于级联式单相VIENNA电路,直流电压应大于交流电压峰值的2倍,假设直流电压为2 000 V,那么二级级联的单相VIENNA开关变换器每级承受的直流电压为1 000 V,开关管承受的电压为直流电压的一半,即500 V。为了保证安全运行及对器件的耐压要求可选用1 200 V及以上的IGBT。
级联式单相VIENNA开关变换器还可以用级联H桥代替[19]。级联H桥每级含有4个全控型器件,比级联式单相VIENNA开关变换器每级多3个全控型器件,开关损耗更大,需要增加相应的驱动控制电路;而级联式单相VIENNA开关变换器虽然每级采用6个二极管,但在任意时刻有且仅有2个二极管处于工作状态,在高压大功率应用场合,二极管的功耗几乎可以忽略不计。因此,采用级联式单相VIENNA开关变换器结构有助于提高系统效率和功率密度。
1.2 级联式单相VIENNA开关变换器原理
如图1所示,级联式单相VIENNA开关变换器拓扑结构由等效单相电源、升压电感L、n个单相VIENNA模块级联构成。每个模块由1个开关管S,6个二极管VD1至VD6,2个直流侧支撑电容Cn1、Cn2和负载电阻构成。
以二级级联的单相VIENNA开关变换器为研究对象,当电感电流iL>0时,在电流连续的情况下有4种工况,如图2所示。
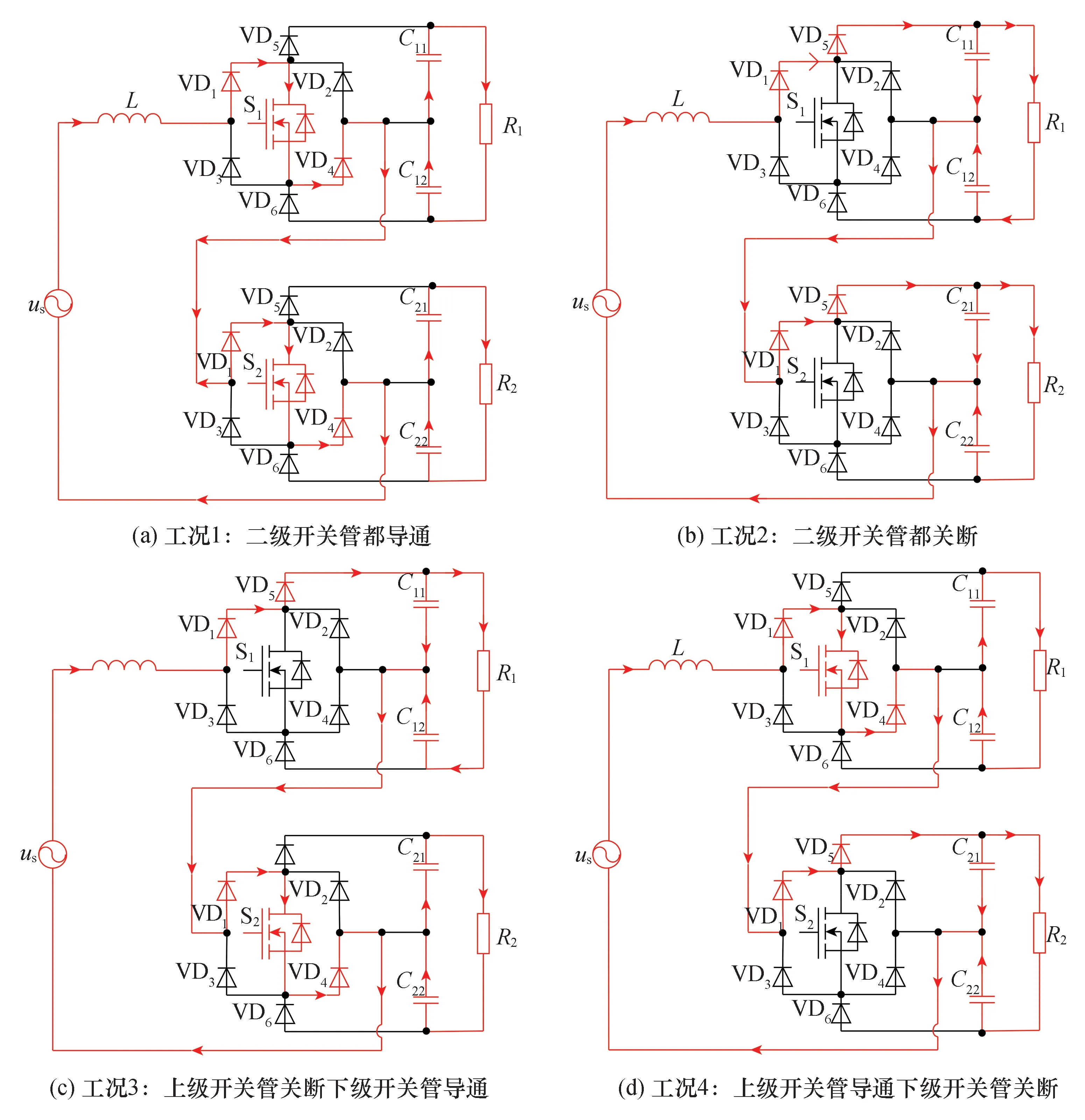
图2 电感电流iL>0时二级级联的单相VIENNA开关变换器的4种工况Fig.2 Four operation modes of two-stage cascaded single-phase VIENNA switching converter when iL>0
工况1:二级开关管都导通。电感电流从电源出发经升压电感L、二极管VD1、开关管S1、二极管VD4后由电容C11、C12中点流入下一级级联电路中,再经过二极管VD1、开关管S2、二极管VD4回到电源,这个过程中电感L充电;负载电阻R1、R2分别由对应的支撑电容C11、C12和C21、C22供电。
工况2:二级开关管都关断。电感电流从电源出发经升压电感L、二极管VD1、VD5后,由电容C11流入下一级级联电路中,经过VD1、VD5、电容C21回到电源,这个过程中电源、电感L和支撑电容共同向负载供电;升压电感L放电。
工况3和工况4:一级开关管导通,另外一级开关管关断。运行情况同单相VIENNA电路,在此不再赘述。
2 级联式单相VIENNA开关变换器的小信号数学建模
对二级级联的单相VIENNA开关变换器进行小信号数学建模,为多级级联的VIENNA开关变换器的小信号建模奠定基础。
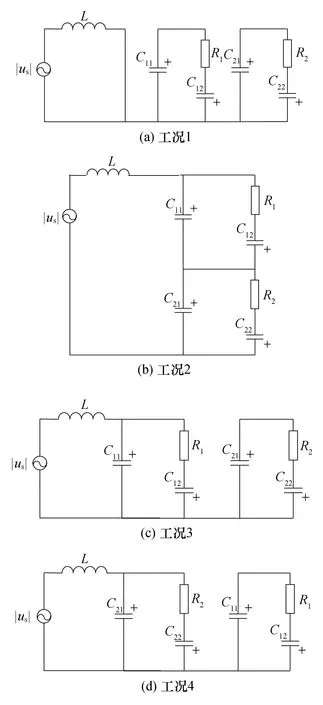
图3 4种工况等效电路Fig.3 Equivalent circuits of all operation modes
图3为二级级联的单相VIENNA开关变换器的4种工况等效电路。为了进一步简化分析,做如下假设:① 整个电路工作在电流连续模式下;② 开关频率足够高,升压电感的电感量较低;③ 开关管和二极管均为理想器件;④ 当采用载波移相控制时,上下级的载波相位相差半个周期,但调制波相同,因此上下级占空比相同,设占空比为d;⑤ 当电路工作在稳态情况下,认为4个支撑电容的电压稳态值均为UC;⑥ 电路工作在负载平衡的情况下,即2个负载电阻的阻值均为R。
由工况1等效电路,有
(1)
式中,iL为升压电感L的电流;r为串联等效电阻;us为等效单相电源。
由于电路工作于稳态情况下,4个支撑电容容值相同且设为C,其端电压均为uC,有
(2)
由工况2等效电路,有
(3)
(4)
由工况3或4等效电路,有
(5)
当电路处于工况3时,上级电路满足式(4),下级电路满足式(2);当电路处于工况4时,上级电路满足式(2),下级电路满足式(4)。
图4为二级级联的单相VIENNA开关变换器载波移相示意图,其中Vr为三角波的幅值。在一个周期T内,当占空比d<0.5时,如图4左半部分,处于工况3或4的时间均为dT,处于工况2的时间为(1-2d)T;当占空比d≥0.5时,如图4右半部分,处于工况3或4的时间均为(1-d)T,处于工况1的时间为1-2(1-d)T。
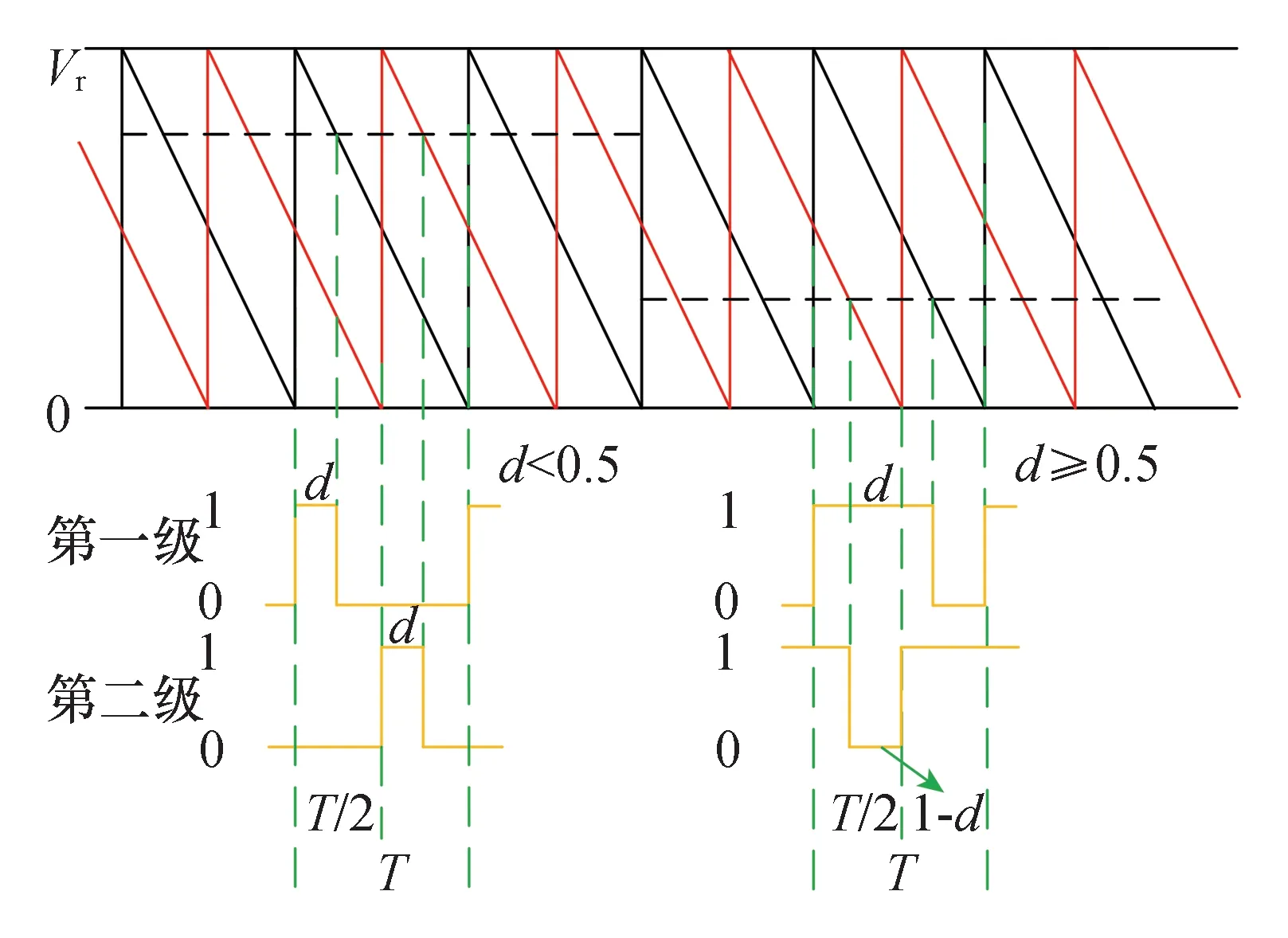
图4 二级载波移相示意图Fig.4 Diagram of phase shifting of two stages
根据式(1)至式(4),在周期T内,当d<0.5时,有
(6)
(7)
在周期T内,当d≥0.5时,有
(8)
(9)
式(6)和式(8)相等,式(7)和式(9)相等。考虑电感电流iL>0和iL≤0的2种情况,由式(7)和式(9),有
(10)
由式(10)得到二级级联的单相VIENNA开关变换器平均电路模型如图5所示。
在系统稳态工作点附近施加一个低频小扰动,令
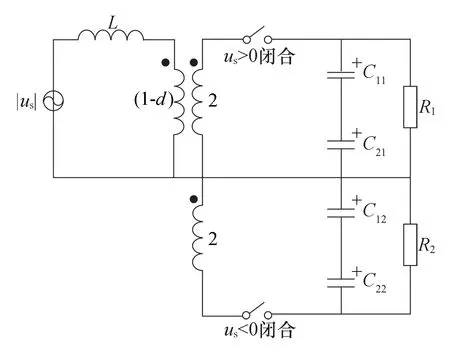
图5 二级级联的单相VIENNA开关变换器的平均电路模型Fig.5 Average model of two-stage cascaded single-phase
(11)
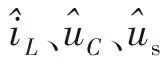
将式(11)代入式(10),并提取其中的交流小信号分量,有
(12)
(13)
3 系统参数及控制策略设计
3.1 系统控制结构
二级级联的单相VIENNA开关变换器设计的主要参数见表1。

表1 设计参数Tab.1 Simulation parameters
为了使设计更为直观,图7提供了整个系统的小信号扰动下的控制框图。
3.2 电流内环参数设计
电流内环的控制框图如图8所示。其中, 根据设计参数确定各传递函数的表达式。
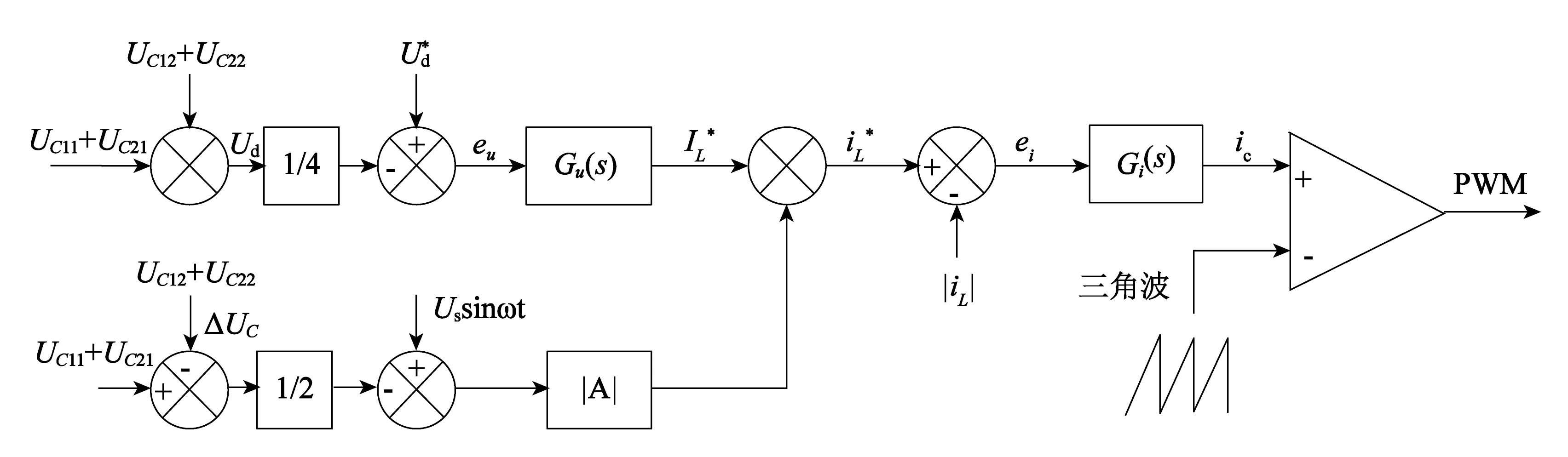
图6 控制框图Fig.6 Scheme of control strategy

图7 小信号扰动下的控制框图Fig.7 Scheme of small-signal perturbation
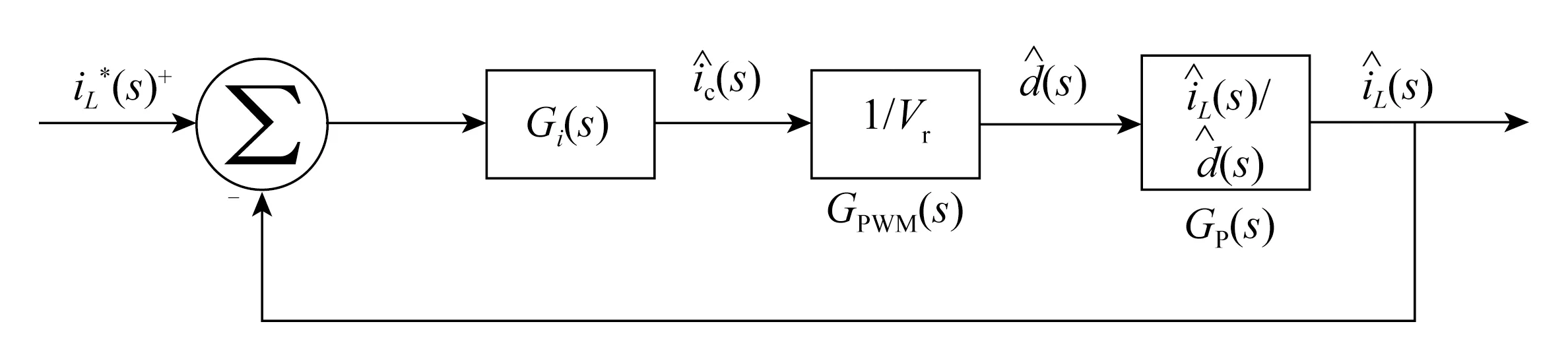
电流信号的参考值;Gi(s)—电流内环的补偿网络;电流的控制量;1/Vr—PWM发生器的传递函数;Vr—三角波的幅值; (s)—控制占空比信号; (s)—功率级输入传递函数;实际电感电流图8 电流内环控制框图Fig.8 Current inner loop control block diagram
PWM发生器实质上是一个比较器,当控制信号ic大于三角波时,输出脉冲信号为1;否则,为0。因此脉冲的占空比为
(14)
在稳态工作点加入小信号扰动后,有
(15)
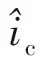
将式(15)代入式(14),有
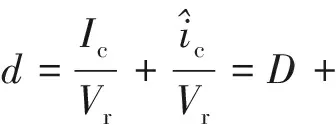
(16)
故只考虑小信号且三角波幅值Vr=1.8 V时,PWM发生器的传递函数GPWM(s)为
(17)
根据小信号模型式(13)可知
(18)
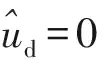
(19)
由设计参数可知,支撑电容电压的稳态值Ud=2 000/4=500 V且升压电感L=2 mH,有
(20)
由GP(s)可得到穿越频率ωci=5×105Hz。
在电流内环中,功率级传递函数GP(s)为Ⅰ型系统,PWM发生器的传递函数GPWM(s)是一个比例环节,当补偿网络的传递函数Gi(s)含有一个积分环节时,Ⅰ型系统提升为Ⅱ型系统,有利于提高系统的控制精度,但此时系统的相位裕度为0°。为了提高相位裕度,Gi(s)应当含有一对零极点进行调整。因此设补偿网络传递函数Gi(s)为
(21)
式中,ωz为零点角频率;ωp为极点角频率;ki为电流环比例增益。
一般要求相位裕度不小于40°,幅值裕度不小于2[20]。设所期望的相角裕度φPM=50°,采用“K值法”得到补偿网络的传递函数[21]为
(22)
(23)
ωp=ωciKboost=1 373 740 Hz
(24)
式中,Kboost为中间过程增益系数。
比例增益不会影响相频特性,因此,通过调节比例增益,可以调节补偿后系统的穿越频率,使穿越频率等于相频特性最高点所对应的频率以获得最大的相角裕度。配置比例增益ki为3.411×105,得到补偿网络传递函数为
(25)
则整个电流环的传递函数GLi为
GLi(s)=Gi(s)GPWM(s)GP(s)kFB
(26)
当反馈系数kFB=1时,则有
(27)
图9为整个电流环的Bode图,可以看出相位裕度达到50°,幅值裕度为无穷大,符合设计要求。
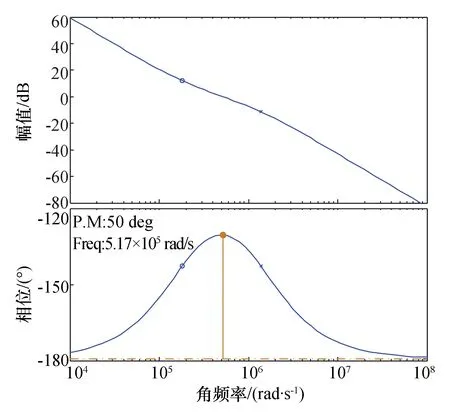
图9 电流内环Bode图Fig.9 Bode plot of inner current loop
3.3 电压外环参数设计
根据交流侧输入和直流侧输出功率守恒原理,并忽略升压电感L的压降,有
(28)
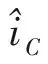
又有
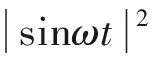
(29)
忽略稳态值和2倍频信号,由式(28)和式(29)得
(30)
又有
(31)
(32)
由式(30)至式(32),得
(33)
(34)
设电压环补偿网络传递函数为Gu(s),则有
(35)
式中,ωcu为极点角频率;ku为电压环比例增益。
设计整个电压环在2倍频处(100 Hz)穿越,且该处的模值为2倍频等效电阻,同时单个模块的输出功率为25 kW,2倍频波动限制在1.5%以内,则有
(36)
IL2nd=0.015IL=0.698 7 A
(37)
(38)
由式(36)至式(38)可求得
ωcu=1.23,ku=0.217 6
(39)
整个电压环传递函数GLu为
(40)
图10为电压环Bode图,可以看出相位裕度达到79.6°,幅值裕度为无穷大,符合设计要求。
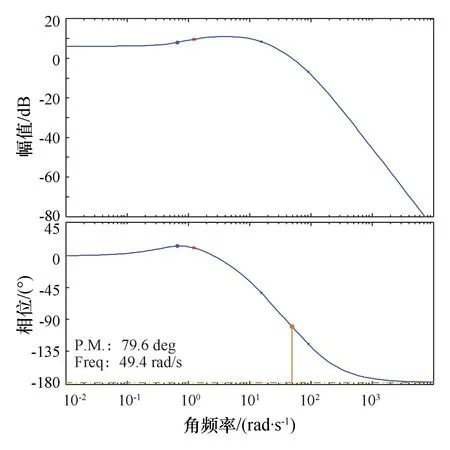
图10 电压外环Bode图Fig.10 Bode plot of outer voltage loop
4 仿真分析
为验证所设计的电流内环和电压外环补偿网络的可行性,通过在Matlab/Simulink 环境下搭建系统的仿真模型进行验证。三相系统仿真参数见表1,控制器参数采用第3节中的参数设计。
图11为系统三相电压和电流波形。系统开始处于稳态,0.3 s时相电压由660 V突变为560 V, 0.4 s时三相负载功率由150 kW突变为120 kW,在其扰动中,整个系统始终保持单位功率因数运行,这表明电流环设计合理。
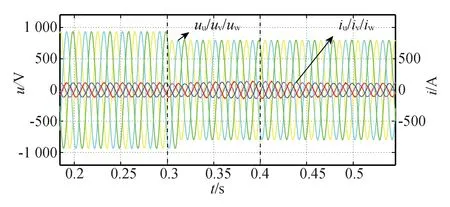
图11 三相电压和电流波形Fig.11 Three phase voltage and current
图12为单级模块输出直流电压。系统开始处于稳态,0.5 s时交流输入相电压由660 V突变为560 V,1 s时三相负载功率由150 kW突变为 120 kW,系统在其扰动后输出的直流电压可以迅速调节至稳态值,且稳态直流电压波动较小,这表明电压环设计合理。
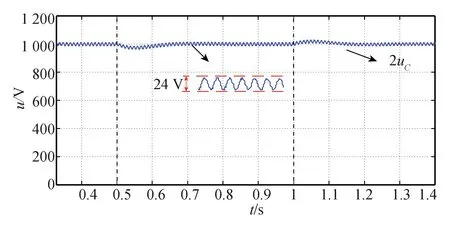
图12 输出直流电压Fig.12 DC voltage of output side
5 结 论
(1) 提出一种由三个级联式单相VIENNA开关变换器星接组成的三相整流电路,并作为矿用高压变频器的整流级。该整流级可以直接与高压交流电网相连,取消了传统矿用高压变频器整流级前端昂贵而笨重的工频变压器,降低了变频器的成本,减轻了变频器的体积和质量。
(2) 考虑到煤矿主通风机不需要反馈能量,采用能量仅单向流动的VIENNA电路,可以减少开关器件的数量,进一步降低了开关器件的损耗和成本。
(3) 对级联式单相VIENNA开关变换器进行小信号建模研究,在此基础上进行了电压环和电流环补偿网络参数设计,同时在Matlab/Simulink平台上进行了仿真验证,证明本文所提出的级联式单相VIENNA开关变换器的小信号模型的正确性。
