一维光子晶体无序膜厚扰动的分析及优化
2020-01-06赵晓丹王同林张明达杨毅彪
赵晓丹,王同林,张明达,杨毅彪,2
1)太原理工大学物理与光电工程学院,山西太原 030024;2)太原理工大学新型传感器与智能控制教育部重点实验室,山西太原 030024
多层光学薄膜是在光学器件或电子元件表面,用物理或化学的方法堆叠沉积形成的非常薄的结构层.其中,光子晶体是由不同折射率的介质材料在空间上周期排列形成的特殊光学薄膜结构.利用反射和折射的原理可以控制光在光子晶体中的传播,实现反射或滤波的效果.光子晶体可广泛应用于反射膜[1-2]、滤光膜[3-6]、传感器[7]及激光器[8]中.
受限于目前的微加工技术水平,制备大尺度、高质量的光子晶体比较困难.现有理论研究多偏重于高质量因子的光子晶体设计[9-10].然而,理论上预期的薄膜光学质量比实验测量结果要高很多[11],这是由于要展现光学薄膜特性,膜层厚度必须按一定的排列顺序精确控制.然而实验制备过程中,要达到理论模拟要求的完美膜层结构并非易事.实验过程中不可避免的存在系统误差和随机误差[12-13],这会降低纳米光子器件的性能[14-15],从而引入损耗或安德鲁局域效应[16].
SULLIVAN等[17]利用3种不同物理气相沉积方法制备光学滤波器,提出不同监测策略优化计算结果,但误差分析最大值仅为3%.而在工业生产中,3%的膜厚误差并不能契合实验结果.GARCIA等[18]在光子晶体波导中,实验证明了一种量化无序方法,但其计算并没有考虑材料色散,且其计算的误差分析最大仅为0.1a(a为晶格常数).
针对实验中的膜厚随机误差,本研究在周期性光子晶体模型中引入服从高斯分布的随机膜厚扰动,并讨论周期数和两种介电材料的膜厚浮动对光子晶体光学性能的影响.通过对比理论与实验的透射谱线,提出一种补偿膜厚扰动的优化方案.该方案可以保证禁带中心位置不发生过大偏移,同时可降低制备精度要求,降低工业生产成本.
1 结构模型和计算方法
通过传递矩阵法(transfer matrix method,TMM)分析结构光学性质.第k层特征矩阵可表示为
(1)
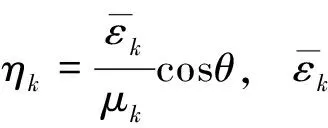
在实际镀膜过程中,光子晶体膜层的厚度会在设计值附近浮动.周期性无序扰动的薄膜模型是指在周期性结构的基础上,周期单元的厚度相对设计值有一定偏移.采用期望值为0,方差为σ2的正态分布来描述厚度随机波动的情况.每一层薄膜的实际厚度为
d实际=d设计±Δ0
(2)
其中,d设计为膜层的设计厚度;Δ0为薄膜厚度的随机偏差值,服从期望值为0,方差为σ2的正态分布.根据高斯分布的定义,Δ0落在(0-σ,0+σ)内的概率为68.268 949%.
本研究采用如图1(a)所示的(Si/SiO2)N结构光子晶体模型,其中,N为周期;晶格常数a=110 nm;Si薄膜的厚度为dSi=0.34a;SiO2薄膜的厚度为dSiO2=0.66a.模拟考虑Si和SiO2的色散[19-20].图1(b)为光子晶体的本征能带,其禁带位于446~670 nm,禁带宽度为224 nm.由于Si在450 nm以下有吸收,所以模型的透过率在450 nm以下近似为0.
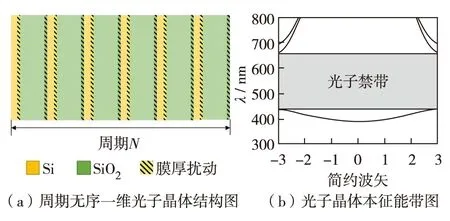
图1 结构能带示意图
2 结果与讨论
2.1 周期数对光学性质的影响
通过比较不同σ的高斯分布分析相应的透射谱.模拟在σ=0.20a时,不同周期数对透射性能的影响,结果如图2.
由于Si材料的吸收,450 nm以下为吸收禁带,图2(a)的光子禁带位于500~670 nm.由于模拟中采取随机误差,禁带位置会在本征能带附近随机偏移.随着层数的增加,整个膜层的无序性增加,薄膜系统变得复杂.随着误差变大,透射率发生复杂波动.禁带宽度变得不稳定,但总体趋于变窄.当层数较大时,某一层的微小误差也会导致整个系统光学性能的改变.另一方面,如果材料的吸收系数不为0,系统的透光率将随着层数的增加而降低.因此,制备光子晶体时应根据精度要求选择合适的周期数.
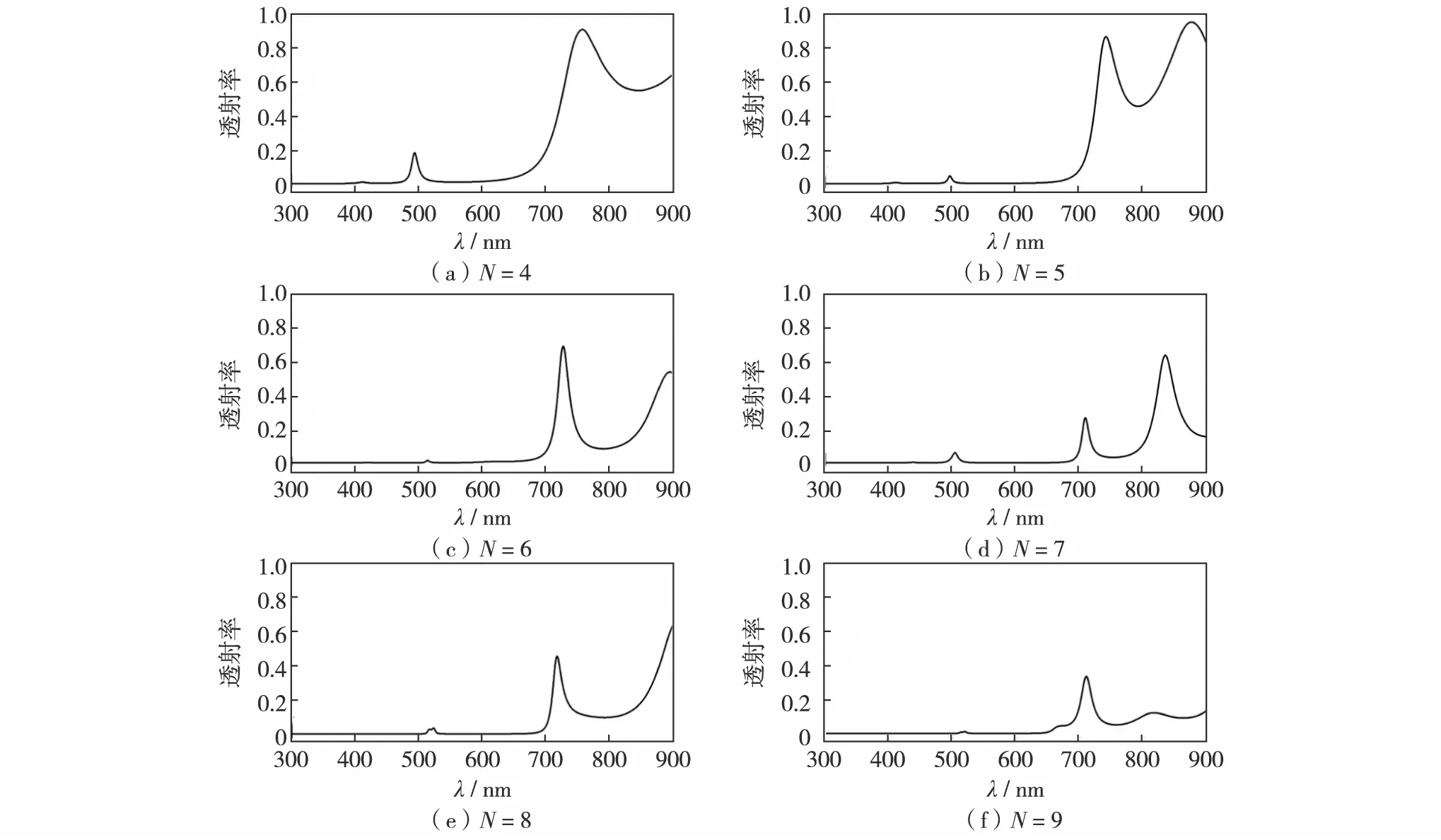
图2 周期数对光子晶体透射性能的影响
2.2 两种材料对光学性质的影响对比
本研究选取N=6,研究随机误差在-0.2a~0.2a时,光子晶体禁带宽度及透过率随Si及SiO2层的厚度变化的变化情况,结果如图3.
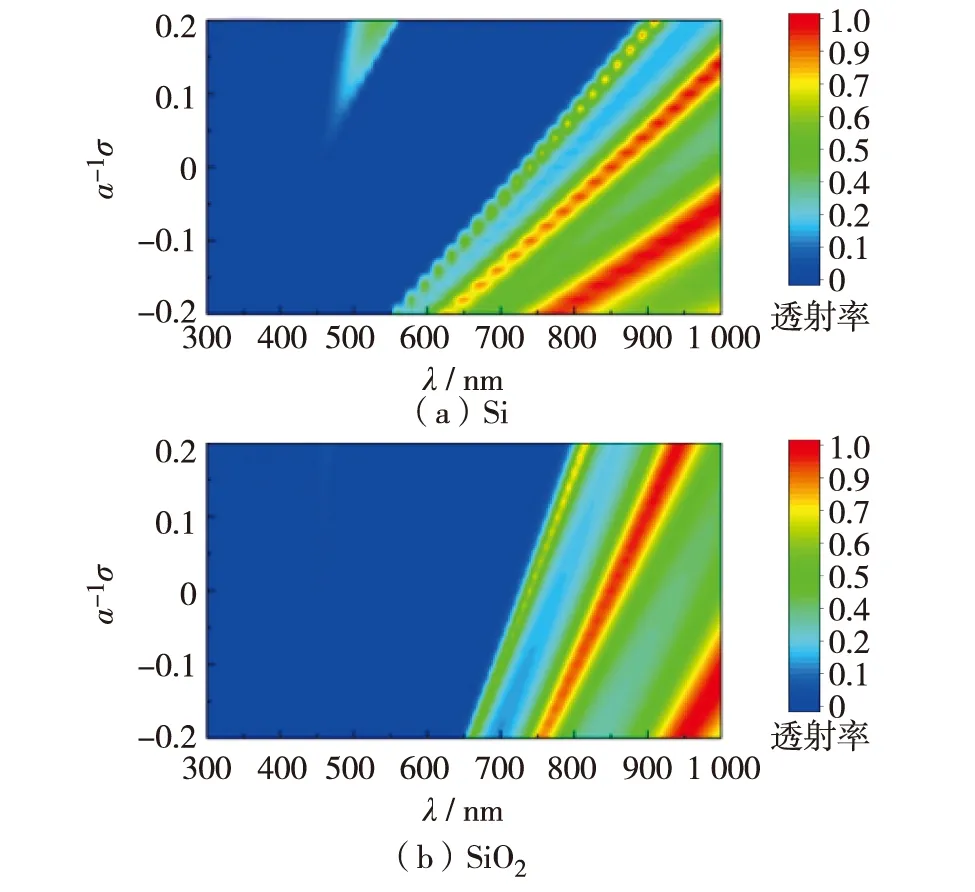
图3 两种薄膜膜厚误差不同时,禁带位置的变化
由图3可见,随着Si层厚度的增加,光子禁带由446~670 nm红移至572~853 nm,禁带宽度由224 nm增至281 nm,增加了25.45%.当SiO2层厚度增加时,光子禁带由446~670 nm红移至476~765 nm,禁带宽度由224 nm增至289 nm,增大了29.02%.对比图3(a)和(b)可见,光子晶体的禁带位置对Si层厚度的变化较为敏感.这是由于Si的折射率较大,当物理厚度变化相同时,Si的光学厚度改变更大,导致禁带漂移较大.当禁带红移量大于50 nm时,光子禁带与该膜层的吸收禁带重合,形成超宽禁带的带阻滤波.对于光子晶体层数较少的简单系统,薄膜厚度误差对系统光透射率的影响较小,禁带位置会发生漂移,并与误差成线性关系.禁带宽度则对SiO2层较为敏感.
根据理论设计的(Si/SiO2)N结构模型,本研究采用型号为JGP-450B的磁控溅射镀膜仪实验制备光子晶体多层膜样品.基底采用2 cm×2 cm的高纯石英玻璃,靶材采用纯度为5N的Si和SiO2,本底真空度为4.0×10-4Pa,采用型号为STM-2XM的膜厚仪控制膜层的厚度.选定N=6,在高纯石英玻璃基底上交替镀Si和SiO2薄膜.采用功率为40 W的射频磁控溅射制备Si,采用功率为60 W的射频磁控溅射制备SiO2.制备的光子晶体样品利用R1角分辨率光谱仪测量其透射谱.
理论模拟不同膜厚随机波动幅度的光子晶体透射性能.对于a=110 nm的光子晶体结构,选取σ分别为0.01a、0.05a、0.10a、0.15a、0.20a及0.25a的随机膜厚误差,并分别对Si和SiO2层进行讨论.将模拟数据与光子晶体实验样品的测量透射谱进行对比.图4为实验和理论光子晶体透射对比图.其中,SiO2层保持dSiO2=0.66a不变,仅改变每层Si的厚度.
从图4可见,存在厚度扰动的光透过率曲线与设计值相差较大,其原因在于光子晶体多层膜系的每一层均存在误差,因此,整个系统的光学相位就会因误差累计而发生变化.层数越少,累计的光学相位误差越小,误差对光透射性质的影响也就较小.由于设计的误差值为随机误差,禁带位置会在能带附近随机摇摆.图5为保持Si层的dSi=0.34a不变,仅改变每层SiO2的厚度时,膜厚误差对禁带宽度的影响.相比于Si层的厚度误差,SiO2层的误差对透光率的影响较小.这是由于SiO2作为低折射率材料,膜厚误差所引起的光学误差较小.
图6对比两种材料误差对禁带宽度的影响.当Si层扰动σ=0.01a时,禁带宽度为本征能带的111.16%;当Si层扰动σ=0.25a时,禁带宽度仅为37.67%.当SiO2层扰动σ=0.01a时,禁带宽度为本征能带的111.56%;当SiO2层扰动σ=0.25a时,禁带宽度为76.83%.可见,Si的误差值对光子晶体的禁带宽度影响较大,说明光子晶体的禁带宽度对折射率较大材料的膜厚变化较为敏感.由于膜厚偏差为随机误差,禁带宽度的偏移不是线性的.但总体趋势呈线性关系,而且会越来越趋近于光子晶体材料的本征光子能带.光子晶体本征能带宽度为224 nm,而当厚度偏差σ<0.10a时,禁带宽度超过了本征能带宽度.这是因为引入了膜厚的高斯扰动,相当于将不同频域的光子晶体进行禁带叠加.当随机偏差较小时,会使禁带宽度略微拓宽.
3 膜厚补偿方案
为降低光子晶体多层膜的实验制备难度,根据Si和SiO2的折射率,设计一种对薄膜厚度的补偿优化方案.通过研究上述厚度扰动与透射率的关系,发现在同一周期内,一种材料膜厚误差可用另一种材料的厚度弥补.选择中心波长为450 nm,对应两种材料折射率为nSi=4.673 0,nSiO2=1.471 3.由于nSi≈3nSiO2,要保证光学厚度相同,Si层膜厚的浮动需要通过3倍SiO2厚度来补偿;反之,SiO2层膜厚要用1/3的Si厚度来补偿.实验中每完成一层镀膜后,用光度法[21]测量其膜厚,根据实测值和标准值的差值确定下一层厚度,具体的流程如图7.
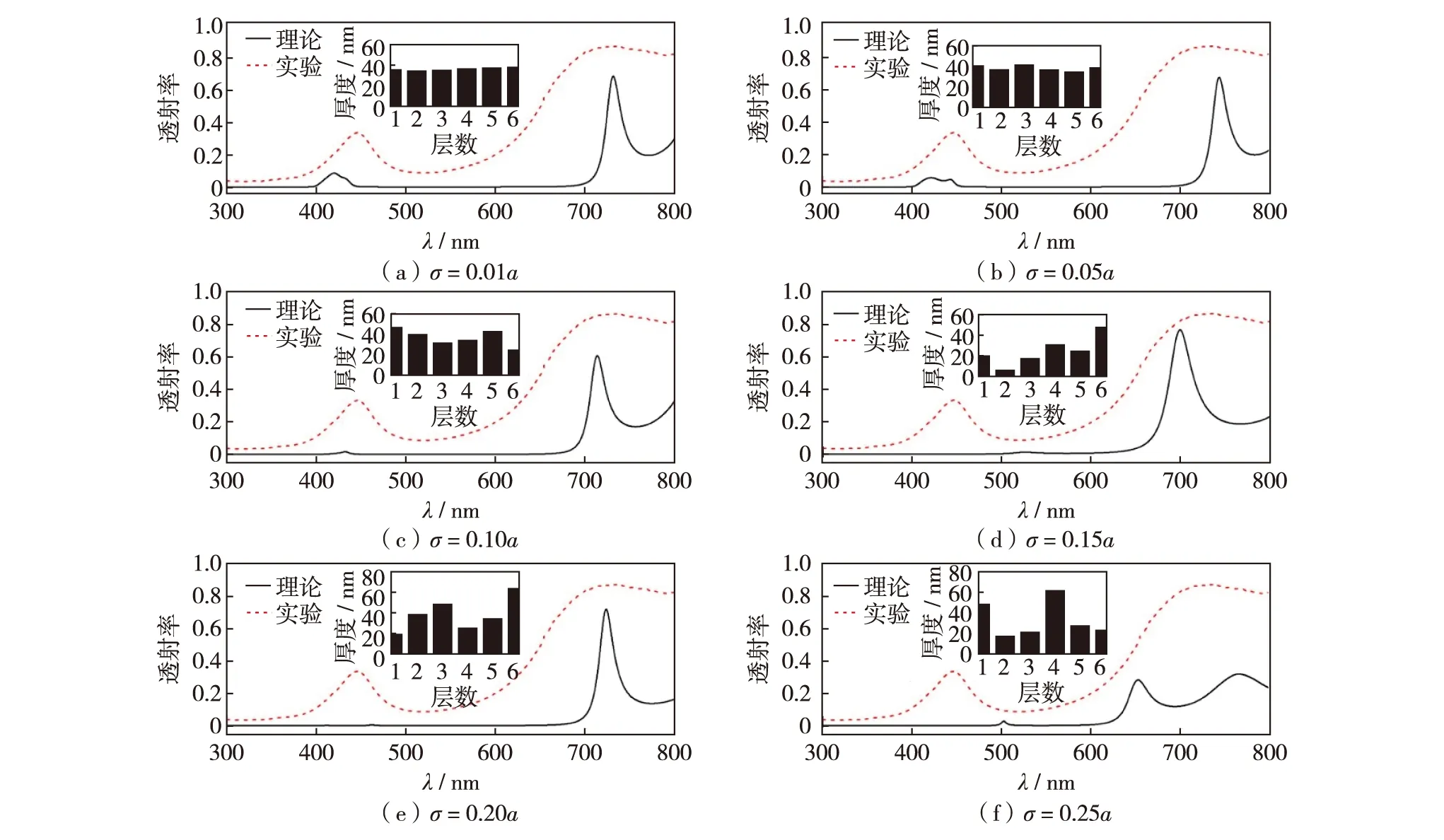
图4 Si层膜厚误差对光子晶体透射性能影响的理论和实验对比

图5 SiO2层膜厚误差对光子晶体透射性能影响的理论和实验对比

图6 膜厚误差对禁带宽度的影响
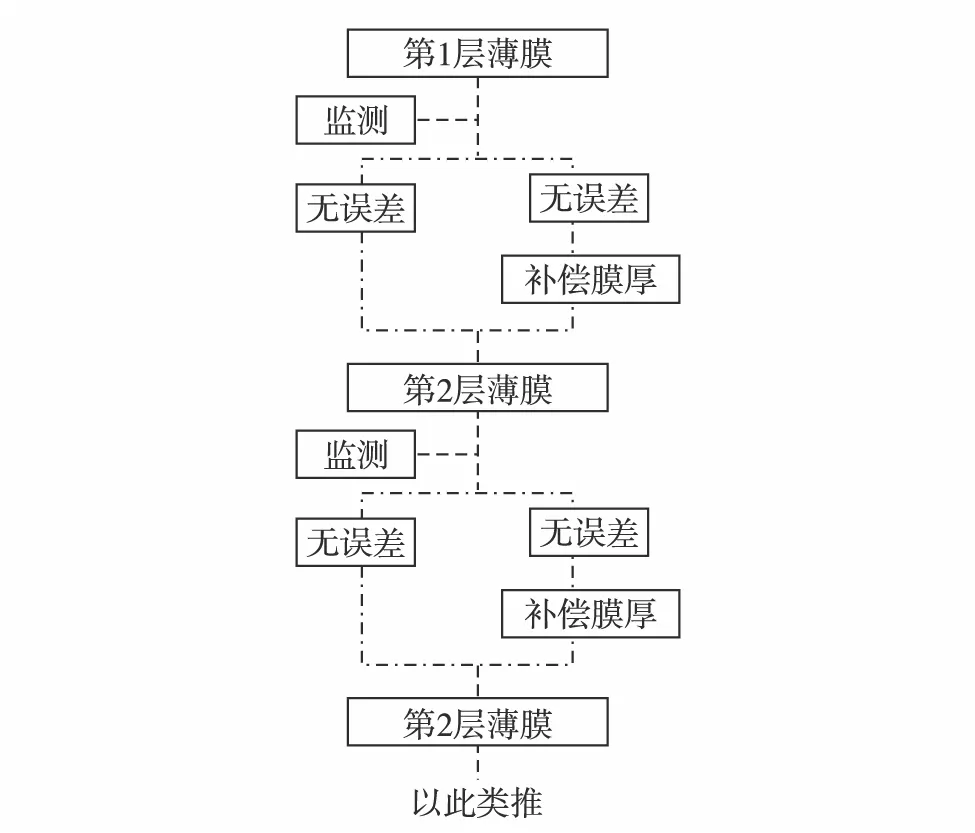
图7 膜厚补偿优化方案流程
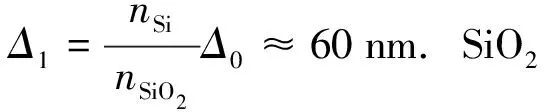

图8 不同膜层厚度计算值下透射光谱叠加图
实验验证此膜厚补偿方案.采取磁控溅射镀膜仪制备单层膜后,测量单层膜的厚度,第2层膜厚采用补偿后的膜厚进行制备,以此类推.样品制备好后,用R1角分辨率光谱仪测量优化后的光子晶体透射谱,并与模拟计算中σ=0.2a的透射谱进行对比,结果如图9.
由图9可见,理论与实验曲线重合度较好,透射谱的中心波段和禁带宽度均吻合.证明该方案可以补偿光子晶体膜厚的随机误差,保证纳米光电子器件稳定的禁带位置和宽度.这种补偿方案的技术难度低,适用于不同材料光子晶体的优化,可为实验制备低成本薄膜系统提供理论指导.

图9 补偿后理论与实验对比
结 语
本研究针对光子晶体周期性镀膜时存在的膜厚微扰,在一维光子晶体模型中引入一个服从正态分布(期望为0,标准差为0.01a~0.25a)的膜厚伪随机误差,构建一种更接近真实情况的周期性无序扰动光子晶体模型.分析周期数对无序结构光学特性的影响,认为随着周期数及光子晶体层数增加,系统的无序性也会相应增加.因此,在保证禁带宽度的前提下,要采用尽量少的周期数.将模拟结果与实验制备光子晶体的透射曲线进行对比,分析两种材料膜厚变化对光学特性的影响.Si作为高折射率层,当膜厚微扰较大时,产生的光学厚度变化较大,光子晶体的禁带偏移量较大.相比于SiO2层,禁带位置对Si层更敏感.而禁带宽度对SiO2层较为敏感.当随机误差较小时,光子晶体禁带宽度会略微展宽,相当于将不同禁带位置的光子晶体进行叠加.最后,为降低实验难度,根据材料折射率,设计一种对薄膜厚度的补偿优化方案,即在同一周期内,一种材料的薄膜镀膜后,根据真实值和实验值的偏差,可用另一种材料的薄膜厚度进行补偿.结果表明,该补偿方案适用于不同材料光子晶体的优化,可以保证纳米光电子器件稳定的光学性能.该方案可以补偿仪器精度不足的问题,其技术难度低,镀膜成本小.
