基于改进蚁群算法的多目标路径规划研究

马小铭 靳伍银

摘   要：传统蚁群算法因在复杂环境中容易产生死锁，导致部分蚂蚁失效，造成效率低下，迭代次数增多。为此，提出了一种利用环境信息引入环境因子来调整启发函数的方法从而降低死锁情况的发生，增加了有效蚂蚁的数量，从整体上提高了蚁群的搜索速度，扩大了搜索范围。同时，传统蚁群算法在路径规划中仅在理想地域内寻求最短路径，而多因素环境中最短路径往往并非最优解。为解决此问题通过在不同环境中对转移概率进行加权优化在追求路径最短的基础上提出多目标路径规划，丰富了蚁群算法的实用性和现实意义。最后经仿真实验对优化算法进行验证，证明了上述优化的可行性。

关键词：蚁群算法;避障;多目标;栅格法;路径規划

中图分类号：TP242                                        文献标识码：A

Mulit-objcctive Path Planning Based

on Improved and Colony Algorithm

MA Xiao-ming ，JIN Wu-yin

（School of Mechanical and Electronical Engineering，Lanzhou University of Technology，Lanzhou，Gansu 730050，China）

Abstract：Traditional ant colony algorithm is prone to cause failure by deadlocks in complex environments. A novel method is proposed to solve the problem，which adjusts the heuristic function by introducing environmental factors according to environmental information，increased the number of ants effectively，improved the search speed of ant colony，and expanded the search range. Aiming at the limitation of traditional ant colony algorithm in pursuit of shortest path in the ideal region in path planning，and the shortest path in the multi-factor environment is often not the optimal solution，the multi-objective path planning is proposed based on the weighted optimization of transition probability in different environments on the basis of the shortest path，which enriches the practicality and practical significance of the ant colony algorithm. Finally，the simulation experiment of optimization algorithm proves the feasibility of the method.

Key words：ant colony algorithm;obstacle avoidance;multi-objective;grid method;path planning

路径规划是指在有障碍物的工作环境中寻找一条从起点到终点的避开所有障碍物的运动路径。它是智能移动机器人领域的重点研究方向之一，是其行为决策的关键技术[1]。路径规划结果的优劣，将直观地对机器人运动过程的流畅性及结果造成影响[2]。而全局路径规划是在已知全局环境信息的情况下，事前规划一条规避障碍的最优路径。常见的移动机器人全局路径规划算法主要有Q-learning算法[3]、神经网络法[4]、遗传算法[5]、蚁群算法等[6]。相比其他算法蚁群算法采用正反馈机制引导整个系统向最优解的方向进化，具有较强的鲁棒性[7]，更加广泛应用于解决旅行商问题（TSP）、车辆路径问题（VRP）[8]等方面，因此蚁群算法也越来越受到研究者的关注[9]。然而蚁群算法仍存在易死锁和易陷入局部最优等缺陷。

介绍了传统蚁群算法的背景原理以及系统模型，然后针对传统算法中的不足与缺陷通过利用环境信息引入环境因子来调整启发因子降低死锁次数，提高蚂蚁的有效率和搜索速度。同时，在栅格法环境建模过程中增添加权路径并对转移概率进行优化，实现多目标路径规划。最后对优化后的蚁群算法与传统蚁群算法进行实验仿真对比，验证了本优化算法的有效性。

1   蚁群算法基本原理

自1960年提出仿生学后，人们模仿生物体内功能机理提出许多新的仿生算法。1990年初期，受蚂蚁觅食过程的启发，Dorigo M首次提出蚁群算法[10]。该算法模仿蚂蚁在觅食过程中释放一种特殊的可挥发分泌物来引导其他的蚂蚁的行为。经过一段时间，距离较短的路径上保留的分泌物会多余其他路径。此后所有蚂蚁都会沿分泌物较浓的路径觅食。

蚁群算法中蚂蚁根据各节点的信息素和启发信息来选择下一节点[11]。蚂蚁k从i点转移j点的转移概率为P  kij，计算公式如下：

P kij = ■，s∈allowk     （1）

式中：allowk表示蚂蚁k下一步允许选择的节点的集合;τij（t）为t时刻节点i到节点j之间的信息素;启发函数ηij（t） = 1/dij，其中dij为节点i与节点j之间的距离，由此可知节点间的距离越近，转移概率越大;α和β两个参数分别反映了蚂蚁选择路径过程中信息素浓度和启发信息的相对重要性。

蚂蚁经过ij释放信息素的同时，信息素也具有挥发的特性。当所有蚂蚁完成一次循环后，每条路径上的信息素浓度也将更新，规则如式（2）所示：

τ（t + 1）=（1 - ρ）τij + ΔτijΔτij = ■Δτ kij，0 < ρ < 1    （2）

式中，ρ为挥发系数，ρ值越大，信息素挥发越快，避免信息素的无限累加。Δτij表示所有蚂蚁在ij路径上释放的信息素浓度;Δτkij表示第k只蚂蚁在路径ij上释放的信息素浓度，如公式（3）所示：

Δτ kij=Q/Lk  第k只蚂蚁从节点i到节点j0       其他 （3）

其中，Q为常数，表示蚂蚁一次循环释放信息素的总量;Lk为第k只蚂蚁在本次循环中所走的路径长度。

2   基于蚁群算法的改进

2.1   环境介绍

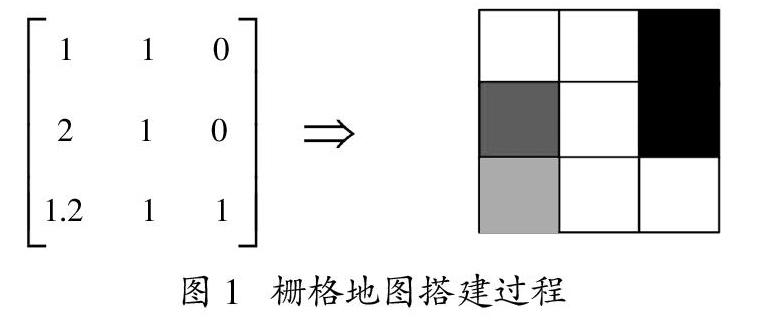
栅格法作为路径规划常见的环境建模方法[12]，实质上是将工作环境进行单元分割，即其用大小相等的方块表示出来。同时将所有方块按照实际需要分为可行区域（白色区域）和障碍物（黑色区域）。为了研究多目标蚁群算法本文将引入带有权重的可行区域（灰色区域）。该部分模拟道路中常见的拥堵、施工、收费等情况，在行进过程中应尽量避开该区域。环境搭建则应用矩阵将每一个元素转化为对应颜色的方格，如图1所示。

2.2   启发信息优化调整

传统蚁群算法在初始阶段，每个节点的信息素都是相同的，蚂蚁在路径选择中主要依赖于启发信息的差异。依据启发函数公式可知蚂蚁倾向于选择距离较近的节点。该方法没有利用全局地图障碍物信息，只依据距离长短布局启发信息，以致在障碍物多，地图复杂的情况下，蚂蚁陷入某一节点并且无下一节点可选择即发生死锁现象，随后的蚂蚁依照之前蚂蚁保留的信息素将会导致越来越多的蚂蚁死锁。

经多次试验证明，在遇到凹形或边界出现L形等障碍最容易引发蚂蚁的锁死。常见的改进方法是将障碍物进行填充处理，消除凹形或边界的L形障碍物。这种方法以修改環境为代价来提高蚂蚁有效率，当环境改变时需要重新建立环境模型。文献[13]通过在不同迭代次数动态自适应调整α、β的值来降低死锁发生率。该方法仅从全局优化的角度出发，没有对容易发生死锁的环境细节考虑。本文在传统启发信息算法中引入环境因子Ej来增强对环境的阅读，有效避免死锁，提高有效蚂蚁的数量。

如图2所示，某节点前往下一节点共有8个方向可供选择，选择过程主要依据节点上的信息素及其启发信息，未考虑节点周边障碍物数量及其分步。因此，本文有效利用全局环境信息，对节点周围障碍物进行统计分析。经试验表明当节点周边出现5个以上的障碍物时，则视该节点容易引发死锁状态。因此对启发函数进行以下调整。

引入环境因子Ej，对启发函数按式（4）和（5）进行调整。当障碍物的点少于5个时，则Ej = 1。当障碍物的点在5个及以上时，Ej > 1更有利于算法的调整。同时，当发生死锁现象，将该只蚂蚁之前路径遗留的信息素清空，防止对后续蚂蚁产生干扰。

该方法目的是在算法初期通过启发函数标记易死锁的点，避免寻找路径的过程中陷入死锁状态，提高了有效搜索次数。随着迭代次数的增加，无效路径上的信息素逐渐挥发，有效路径上已经积累了部分信息素。此时信息素在路径搜索中占据主导地位，因此该优化既有效的避免死锁又提高了收敛速度。

η* = ■       （4）

Ej = 1   节点j周围障碍物个数<5>1   节点j周围障碍物个数≥5 （5）

2.3   转移概率优化

传统蚁群算法主要追求从起点至终点的最短路径，但是在现实生活中路径规划问题不再是单一目标下的优化问题，而转化成了多目标优化问题[14]。多目标优化通常需要在两个及两个以上的目标条件约束下寻求最优解。转移概率主要是依据信息素和启发信息计算从该节点往相邻可行每一个节点的概率。然后采用轮盘赌算法[15]，来确定下一个节点。该方法根据每个节点的概率计算累计概率，然后随机产生一个0～1的数，该数落入的累积概率对应的节点就是下一个被选的节点。如图3所示，当随机数落在P1至P1 + P2端，即选择P2所对应的节点。本文将通过对转移概率的优化，实现在尽可能避开加权路段的同时追求一条最短路径。改进后的概率转移公式如（6）所示。

P *kij = ■，s∈allowk

（6）

式中D（x，y）为节点在栅格矩阵中对应的元素。如果是普通路径则按照栅格环境搭建规则得知D（x，y） = 1，如果该路径是拥堵或收费路段则D（x，y） >1。因此D（x，y）与P *kij成反比，表明蚂蚁更加倾向沿普通路径行走。

为描述多目标路径规划的有效性，权衡最短路径与尽可能较少的经过加权路径之间的关系。本文采用线性加权和法建立新的评价函数，该方法按照各目标的重要性赋予它相应的权系数，然后对其线性组合求解最优路径。如公式（7）所示：

Lbest = D（x，y）（Lp + Lw1 + Lw2 …）         （7）

式中，Lbest为所得路径总长，值越小越接近路径规划的最优解;Lp为普通路径;Lwi（i = 1、2、3……）为加权路径。

3   仿真实验

为了验证上述蚁群优化算法具有可行性和有效性，通过两次仿真实验与传统蚁群算法进行了对比。验证了本算法的优越点。实验中部分参数如表1所示。

3.1   实验一

该实验在20 × 20的栅格中进行，环境中障碍物数量多，分布复杂，多采用蚂蚁容易死锁的凹形障碍物。主要验证环境中优化后的蚁群算法蚂蚁死锁数量下降，提高了蚁群搜索速度。实验结果如图4-10所示。

为验证改进后蚁群算法的优化效果，以及获取Ej的最优值。实验依次对传统算法、文献[13]和不同Ej值的优化算法进行对比。图4-9为各类算法运行10组后所得到的最优路径规划图以及对应的迭代次数与规划路径长度关系图。由实验数据可知改进后的蚁群算法与其他算法相比在规划路径中差异较小，但是优化后的算法经过前期的路径探索，较早获得最优路径并且趋于稳定。图9（a）和图9（b）经过约20次迭代达到最优路径并趋于稳定。图9（c）和图9（d）则在约40次迭代达到最优值并趋于稳定。图9（e）虽收敛早，但未达到最优值。由图5可知传统算法前期探索时间长，在达到最优路径后稳定性差，经过多次浮动迭代至90次才达到最优路径。图7所反映文献[13]在获取最优路径后，未能在最优路径处收敛。

图10比较了10组实验中蚂蚁发生死锁个数的平均值以及波动幅度。由图可知本文算法在不同参数下均有效降低了死锁数量的发生。由公式（8）计算可知，死锁发生率降低了约78%。

降低率=■×100%  （8）

综合收敛速度变化曲线以及死锁数量的误差分析可得，当Ej = 2 - 4时收敛曲线平稳收敛于最优路径，死锁发生数维持在较低水平，误差范围相比其他参数波动较小。因此，优化效果整体优于其他参数。总结原因主要有一下两点：

1）当环境因子取值过小时，由于轮盘赌算法的随机性，对于容易死锁节点的抑制效果不明显。不能有效避开该节点，造成误差波动幅度较大。

2）当环境因子取值过大时，对死锁点的排斥过大，其方法等效于死锁点的填充。缩小了全局路径搜索的范围。

该实验表明本文算法降低了死锁现象的发生，提高了蚁群中有效蚂蚁的数量。同时，消除死锁蚂蚁路径中留下了信息素避免了无效路径中信息素对其他蚂蚁的干扰，加快了最优路径搜索速度。基于上述结论，优化后的蚁群算法增强了蚁群的整体性能，因而路径搜索速度及收敛速度都有所增强。

3.2   实验二

该实验将某地区局部道路图映射在50 × 50的栅格当中。为验证优化后的蚁群算法能实现多目标路径规划，在地图中将带有权重的路径用黄色表示。实验意图规划一条从起点至终点的最短路径，同时能最大限度的规避加权路径。实验结果如图11所示：

图11（a）中蚂蚁受启发函数，沿近似对角方向按阶梯形式到达终点，未能对加权路段有效回避。而图7（b）中经优化后的算法在加权路段具有自主规避性能。

由此得出，优化后的算法能最大限度避开加权路径而且与传统蚁群算法相比路径长度相同。实验结果表明优化后的蚁群算法在多目标路径规划中具有良好的效果。

（a）传统蚁群算法

（b）本文算法

4   结   论

基于蚁群算法提出了新的优化方案，充分利用环境信息优化启发函数，引入环境因子调节节点中的启发信息解决传统算法中死锁个数多，收敛速度慢的缺点。其次，优化转移概率，在环境建模中新添加权路径，着力解决多目标路径规划问题。最后，通过仿真实验将本算法与传统蚁群算法进行了比对，证实了本算法的优点。

参考文献

[1]    史恩秀，陈敏敏，李俊，等. 基于蚁群算法的移动机器人全局路径规划方法研究[J]. 农业机械学报，2014，45（06）：53-57.

[2]    霍凤财，迟金，黄梓健，等. 移动机器人路径规划算法综述[J]. 吉林大学学报（信息科学版），2018，36（06）：639-647.

[3]    王帅. 煤矿井下基于Q-learning算法的移动机器人路径规划[J]. 现代电子技术，2008，31（24）：106-108.

[4]    邓万宇，郑庆华，陈琳，等. 神经网络极速学习方法研究[J]. 计算机学报，2010，33（02）：279-287.

[5]    鞠成恩，赵晓侠，王明兴，等. 基于遗传算法的目标追踪过程中路径规划研究[J]. 传感器与微统，2018，37（06）：112-114.

[6]    俞烨，贺乃宝，高倩，等. 基于改进蚁群算法的移动机器人路径规划[J].  物联网技术，2017，7（3）：46-49.

[7]    LI J，DONG T，LI Y. Research on task allocation in multiple logistics robots based on an improved ant colony algorithm[C].International Conference on Robotics & Automation Engineering. IEEE，2016.

[8]    PAN T，PAN H，GAO J. An improved ant colony algorithm based on vehicle routing problem[C]. Control Conference. IEEE，2015.

[9]    GAN R，GUO Q，Chang H，et al. Improved ant colony optimization algorithm for the traveling salesman problems[J].  Journal of Systems Engineering and Electronics，2010，21（2）：329-333.

[10]  DORIGO M，MANIEZZO V，COLORNI A. Ant system：optimization by a colony of cooperating agents [J].  IEEE Transactions on Systems，Man，and Cybernetics，Part B （Cybernetics），2002，26（1）：29-41.

[11]  柳長安，鄢小虎，刘春阳，等. 基于改进蚁群算法的移动机器人动态路径规划方法[J]. 电子学报，2011，39（05）：1220-1224.

[12]  刘建华，杨建国，刘华平. 基于势场蚁群算法的移动机器人全局路径规划方法[J/OL].农业机械学报，2015，46（9）：18-27.

[13]  裴振兵，陈雪波. 改进蚁群算法及其在机器人避障中的应用[J]. 智能系统学报，2015，10（01）：90-96.

[14]  喻环. 改进蚁群算法在机器人路径规划上的应用研究[D].合肥：安徽大学，2017.

[15]  马振. 改进蚁群算法及其在TSP中的应用研究[D].青岛理工大学，2016.