基于粒子群优化算法的动力定位非线性观测器设计
2020-01-05郭亮琨杨宣访王家林刘蕾
郭亮琨 杨宣访 王家林 刘蕾


摘 要:针对船舶动力定位控制系统中的状态估计问题,提出了一种非线性状态观测器设计方法。采用类Lyapunov方法设计无源观测器,以估计误差的低通滤波信号作为增广状态变量,通过在观测器方程中引入增广状态变量以减少高频运动分量对低频运动参数估计的影响,采用粒子群优化算法对观测器增益矩阵中的9个关键参数进行组合寻优进一步提高观测器动态性能。还以一艘供给船为例进行仿真分析,验证了所设计非线性观测器的有效性。
关键词:动力定位;观测器;粒子群优化
中图分类号:TP273 文献标识码:A
Design of Nonlinear Observer for Dynamic Positioning Based
on Particle Swarm Optimization Algorithm
GUO Liang-kun,YANG Xuan-fang,WANG Jia-lin?覮,LIU lei
(College of Electrical Engineering,Naval University of Engineering,Wuhan,Hubei 430033,China)
Abstract:Aiming at the state estimation problem in ship dynamic positioning control system,a nonlinear state observer design scheme is proposed. The passive observer is designed by Lyapunov-like method,and the low-pass filtered signal of the estimation error is used as an augmented state variable. By introducing augmented state variables in the observer equation to reduce the impact of high-frequency motion components on low-frequency motion parameter estimation,the particle swarm optimization algorithm is used to optimize the nine key parameters in the observer gain matrix to further improve the dynamic performance of the observer. This paper takes a supply ship as an example to analyze and verify the effectiveness of the designed nonlinear observer.
Key words:dynamic positioning;observer;particle swarm optimization
動力定位(Dynamic Positioning,DP)是指船舶不借助锚泊,而是通过自身安装的推进器来抵抗风、浪、流等环境干扰的影响,实现其在海面上固定位置或预期航迹的保持[1]。船舶在海面上运动受到环境干扰的影响可分为由风、流和二阶波浪共同作用所导致的低频运动和由一阶波浪导致的高频运动。由于高频运动仅表现为周期性的小幅摆动和起伏震荡,不会造成船体平衡位置的大范围偏移。为避免不必要的能量浪费和推力器的机械磨损,动力定位控制系统只需针对干扰引起的低频运动进行补偿和控制,而尽量不响应一阶波浪和噪声等高频干扰的作用。但传感器测量系统只能提供带有测量噪声的高低频叠加的船舶位置和姿态信息,为此必须采用观测器对船舶低频运动状态量进行状态估计。在现代控制理论领域,很多学者早已对状态观测器进行了大量研究,包括著名的Luenberger观测器和工程领域广泛应用的Kalman滤波器等[2-3],但多存在需要对数学模型进行线性化处理和鲁棒性不强等问题。非线性观测器设计问题要比线性系统复杂得多,因而引起众多学者的关注[4-7]。
针对水面低速运动船舶采用类Lyapunov 方法设计一种非线性状态观测器,在文献[4][5]的基础上,通过在观测器方程中引入增广状态变量以提高观测器滤波性能,采用粒子群优化算法设计最佳的观测器增益矩阵参数,进一步提高观测器动态性能,最后通过仿真验证观测器设计方案的有效性。
1 船舶运动数学模型
1.1 低频运动模型
对于水面动力定位船舶,一般用纵荡、横荡和艏摇三个自由度的运动进行描述[4]。建立两个坐标系统:随船坐标系xoy和地球坐标系XOY,如图1所示:
可选取η = [x,y,ψ]T,v = [u,v,r]T,船舶三自由度低频运动模型为[4]:
■ = R(ψ)v (1)
M■ = -Dv + RT(ψ)b + τ (2)
式中,M表示系统的惯性矩阵(其包含附加质量),并满足正定要求M = M T > 0;D∈R3×3为线性阻尼系数矩阵,且D > 0;τ∈R3和b∈R3分别表示推进控制力与力矩和环境干扰力与力矩;R(ψ)为坐标转换矩阵:
R(ψ) = cosψ -sinψ 0sinψ cosψ 0 0 0 1 (3)
1.2 环境力模型
环境干扰力通常指风、二阶波浪、流对船舶的作用力。真实海洋环境干扰力在船舶的三自由度上来说十分缓慢,因此环境力模型可由一阶马尔科夫过程描述:
■ = -T -1b + Eb ωb (4)
式中,b∈R3为环境干扰力和力矩;T为三维对角矩阵;Eb∈R3×3和wb∈R3为噪声幅值矩阵和零均值高斯白噪声向量。
1.3 高频运动模型
在实际中,船舶的高频运动是对一阶波浪的响应,通常看作是在三个自由度上附加了阻尼项的二阶谐波振荡器:
hi(s) = ■ (5)
式中,ζi(i = 1,…,3)一般取值為0.05~0.2,为相对阻尼系数;σi和波浪强度相关;ω0i (i = 1,…,3)为波浪PM谱的主导频率。
将其转换为状态空间形式,得到船舶高频运动模型:
■h = Ah ξh + Eh ωh
ηh = Ch ξh (6)
式中, ξh = [ ξx,ξy,ξψ,xh,yh,ψh]T,ηh = [xh,yh,ψh]T表示三自由度方向上的高频位置和艏向角度;Eh∈R6×3为噪声幅值矩阵;ωh∈R3为零均值高斯白噪声向量;
Ah = 03×3 I3×3-Ω2 -2ΛΩ,Ch = 03×3 I3×3
其中,Ω = diag{ω01,ω02,ω03},Λ = diag{ζ1,ζ2,ζ3}。
1.4 系统模型
系统的测量模型为
y = η + ηh + ωy (7)
式中,ωy∈R3为零均值的测量白噪声;y∈R3为测量输出。
假设1 在观测器设计以及稳定性分析时,忽略其高斯白噪声项[4],即ωb = ωh = ωy = 0。
假设2 由于高频艏摇角度非常小,在转换矩阵的计算中可忽略不计,即R(ψ + ψh) = R(ψ)。
结合以上假设,得到DP系统模型:
■h = Ah ξh
ηh = Ch ξh
■ = R(ψ)v
■ = -T -1bb
M■ = -Dv + τ + RT(ψ)b
y = η + ηh (8)
2 增广无源观测器
2.1 增广无源观测器设计
根据文献[1],结合上述假设和DP系统模型(8),无源观测器方程通常设计如下:
■h = Ah ■h + K1■
■ = R(ψ)■ + K2■
■ = -T -1b■ + K3■
M■ = -D■ + RT(ψ)■ + τ + RT(ψ)K4■
■ = ■ + Ch ■h (9)
式中,■ = y - ■为估计误差,■,■∈R3为低频运动(艏向、角速度)的估计值,■h∈R6为高频运动估计值,K1∈R6×3,K2,K3,K4∈R3×3为观测器增益矩阵。
为提高非线性观测器的精度,利用低通滤波器将估计误差■中的高低频信号分离,在原有观测器方程中,再引入新状态变量,是估计误差■的低通滤波信号:
■g = -T -1gxg + ■ = -T -1gxg + ■ + Ch ■h (10)
式中,xg∈R3,Tg = diag{Tg1,Tg2,Tg3} 为滤波参数。
从xg中可以推导出高通滤波信号:
■g = -T -1gxg + ■ = -T -1gxg + ■ + Ch ■h (11)
公式(10)和(11)经过拉氏变换得到传递函数的形式:
x(i)g(s) = ■■(i)(s)■(i)g(s) = ■■(i)(s),(i = 1,2,3) (12)
要求,ωcgi = ■ < ωoi 即滤波器的截止频率必须要小于波浪谱的主导频率,才能起到滤波作用。加入新状态变量后的增广无源观测器方程如下:
■h = Ah ■h + K1g ■g
■ = R(ψ)■ + K2■ + K2 g xg
■ = -T -1b■ + K3 g xg
M■ = -D■ + RT(ψ)■ + τ + RT(ψ)(K4■ + K4 g xg)
■ = ■ + Ch ■h (13)
式中:K1g∈R6 × 3,K2 g ,K3 g ,K4 g ∈R3 × 3为观测器新的增益矩阵。
2.2 稳定性分析
设■ = v - ■为低频速度、角速度估计误差;■ = η - ■为低频位置艏向估计误差;■h = ξh - ■h为高频估计误差;■ = b - ■为环境干扰估计误差;由DP系统模型(8)和观测器方程(13)可以得到观测器估计误差方程:
■h = Ah ■h - K1g ■g
■ = R(ψ)■ - K2■ - K2 g xg
■ = -T -1b■ + K3 g xg
M■ = -D■ + RT(ψ)■ - RT(ψ)(K4■ + K4 g xg)
■g = -T -1gxg + ■
■ = ■ + Ch ■h (14)
定义■ = [ ■Th,■T,■T,xTg]T ■ = K4 ■ + K4 g xg - ■,可得到:
■ = A■ + BR(ψ)■ (15)
■ = C■ (16)
■ = M-1[-D■ - RT(ψ)■] (17)
式中,
A = Ah-K1 g Ch -K1 g 0 K1 gT -1g -K2Ch -K2 0 -K2 g 0 0 -T -1b -K3 g Ch I 0 -T -1g
B = 0I00,C = [K4Ch K4 -I K4 g]
引理1(正實引理) 假定G(s) = C(sI - A)-1B为n × n维的传递函数矩阵,其中系统是可观可控的。当且仅当存在正定矩阵P = PT和Q = QT满足以下公式时,传递函数矩阵G(s)是严格正实的。
PA + AT P = -Q
BT P = C (18)
通过选择合适的观测器增益矩阵使由公式
(15-16)构成的系统满足正实引理。现选择观测器增益矩阵结构如下:
K1 g = diag{k11 g,k12 g,k13 g}diag{k21 g,k22 g,k23 g},K2 = diag{k31,k32,k33}
K2 g = {k31 g,k32 g,k33 g},K3 g = {k41 g,k42 g,k43 g}
K4 = diag{k51,k52,k53},K4 g = {k51 g,k52 g,k53 g}
参考文献[5],增益矩阵参数的调整规则:
k1ig = 2(ωoi ωci+ωcgi ωoi-2ζi ωcgi ωci)(ζi - ζni)■
k2ig = 2(ω2oi-ωci ωcgi)( ζni - ζi)■
k3i = (ωoi ωci-2ωci ζi ωcgi +2ωci ζni ωcgi)■
k3ig = 2ω2cgiωci( ζi - ζni)■
其中,ωci > ωoi表示陷波滤波器的截止频率;ζni > ζi决定陷波作用,表示为设计阻尼系数;为满足系统严格正实的要求,增益矩阵k3ig,k4的参数只需满足如下不等式:
■≤■< ωcgi < ωoi < ωci(i=1,2,3) (19)
上述公式可以确定增益矩阵k3ig,k4参数的取值范围,但实际取值未知,因此本文选用粒子群优化算法对观测器增益矩阵参数值进行组合寻优,以提高观测器动态性能。
考虑如下的Lyapunov函数:
V = ■■T M■ + ■■T P ■ (20)
对V求导得:
■ = -■■T(PA+ATP)■+■T RT(ψ)BTP ■-
■TR(ψ)■-■■T(D+DT)■ (21)
由于系统传递函数是严格正实的,带入公式(18)可得:
■ = -■■TQ■ - ■■T(D+DT)■ (22)
根据Lyapunov稳定性判据,观测器是全局指数稳定的。
2.3 粒子群优化算法
1995年,美国学者J.Kennedy和R.C.Eberhart被鸟群觅食行为所启发,提出粒子群优化算法(Particle Swarm Optimization,PSO)。很多科学研究灵感都来自于自然界的动植物的行为,PSO与很多进化类的算法相似,其本身不依赖于优化问题的严格数学性质,具有本质并行性,也具有进化和群体智能等优点,是一种基于多个智能体的仿生优化算法[8]。
PSO算法主要源于模拟鸟群的捕食行为。模拟一群鸟飞行觅食行为,鸟之间通过集体的协作达到最优目的。设想在一个场景中,一群鸟在随机搜索食物,但在这块区域内只有一块食物,所有鸟也都不清楚具体的位置,但它们可以感受到离食物的距离,找到食物的最优策略就是根据自身经验判断食物位置和搜索目前距离食物最近的鸟的周围区域。粒子群优化算法也正是从其中得到了启发。
在PSO算法中,将鸟的寻食行为对比到优化搜索,每个寻优问题解都想象成一只鸟,即"无质量的粒子"。而且所有的粒子都可以被判断目前的位置好坏,每一个粒子也赋予记忆功能,能记住所搜索的最佳位置,每个粒子运动中,由速度决定它的运动方向和距离,粒子通过追随自身的个体最好位置与群体的全局最好位置来不断地调整自己的位置信息[9]。
考虑最小化问题,假设N维的搜索空间,M为粒子群规模,则在第t次迭代步为:
第i个粒子的当前位置:
Xi(t) = [Xi,1(t),Xi,2(t),…,Xi,N(t)],将Xi代入适应函数求适应值;
第i个粒子当前速度:
Vi(t) = [Vi,1(t),Vi,2(t),…,Vi,N(t)]
第i个粒子经历过的最好的位置(pbest)表示为:
Pi(t) = [Pi,1(t),Pi,2(t),…,Pi,N(t)]
然后将第i个粒子当前位置的适应值与个体最好位置的适应值相比较,如果优于后者,则令当Pi(t) = Xi(t),否则令Pi(t) = Pi(t-1)。
全局最好位置则是粒子群搜索到的当前具有最好目标函数值的位置,即为:
G(t) = Pg(t) = [Pg,1(t),Pg,2(t),…,Pg,N(t)]
其中,1≤g≤M,也可以表示為gbest(t),其中g = arg ■{ f [Pi(t)]}。
PSO算法的速度和位置的更新公式如下:
Vi, j(t+1)=w·Vi, j(t)+c1·r1,i, j(t)·(Pi, j(t)-
Xi, j(t))+c2·r2,i, j(t)·(Gj(t)-Xi, j(t)) (23)
Xi, j(t + 1) = Vi, j(t) + Xi, j(t) (24)
其中,1≤i≤M,1≤j≤N,t表示第t次迭代,c1和c2为加速度常数,又称学习因子,其中c1指的是粒子指向自身最好位置方向,c2指的是粒子指向全局最好位置;r1,i,j(t)和r2,i,j(t)主要为了增加搜索性,是均匀分布的相互独立的随机数序列,取值范围为(0,1);w表示惯性权重,调节对解空间的搜索范围。通常采用线性递减公式:
w = wstart - ■ × t (25)
式中,t为当前迭代次数,tmax为最大迭代次数,wstart表示初始惯性权重,wend表示终止惯性权重。为保证观测器估计偏差最小,目标函数选取为:
min f(x) = ‖■‖2F (26)
式中,‖■‖F为估计误差矩阵的F-范数。
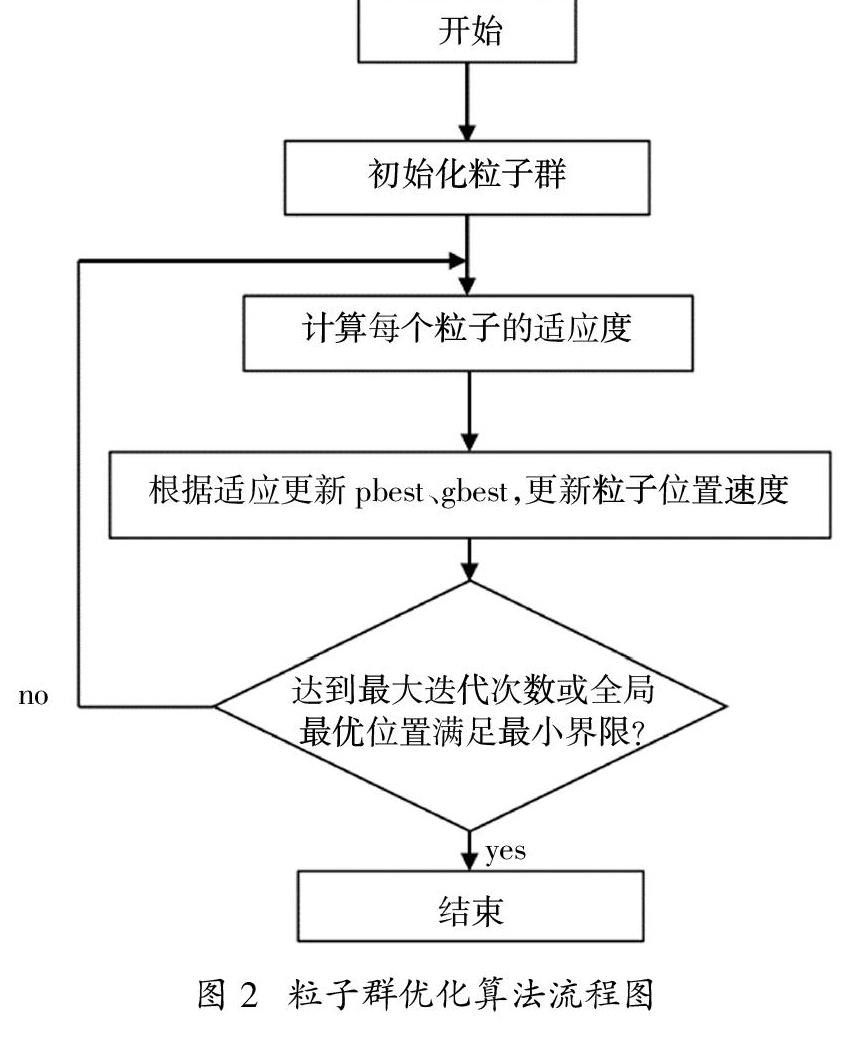
PSO算法流程如图2所示:
3 仿真验证
为了对所设计的增广无源观测器的有效性进行验证,以某供给船为仿真对象进行仿真实验。该船长L=76.2 m,质量m=4.156×106 kg,主要参数为:
M = 5.3122×106 0 0 0 8.2831×106 0 0 0 3.7454×106
D = 5.0242×104 0 0 0 2.7229×105 -4.3933×106 0 -4.3933×105 4.1894×108
环境力模型时间常数矩阵取:
T = 1000 0 0 0 1000 0 0 0 1000
选取船舶高频模型中的相对阻尼系数ζi = 0.1,波浪谱的波峰频率ωoi = 0.89 rad/s,低通滤波器截止频率ωcgi = 0.5 rad/s,设计阻尼系数ζni = 1.0,陷波滤波器截止频率ωci = 1.1 rad/s。
在增广无源观测器中,一阶波浪的频率特性可以直接设计出其中k1 g k2,k2 g中的12个参数,矩阵 k3 g k4,k4 g中的9个参数只能通过经验法反复试凑,观测器增益参数的设置较为繁琐,且难以达到组合最优。为此,采用粒子群优化算法进行寻优,以提高观测器的估计精度。
设置PSO 算法参数如下:
搜索空间的维数N = 9;规模M = 30,加速常数c1 = c2 = 2,最大迭代次数tmax = 100,初始惯性权重wstart = 0.9,终止惯性权重wstart = 0.4。
获得DP船舶仿真结果如图3~图5所示,图中虚线为估计值,实线为期望值。由于篇幅的限制,仅给出纵荡方向的仿真曲线。
从图3~图5可以看出,所设计的增广无源观测器可以准确估计出船舶低频运动分量及高频运动分量,从而可以实现只针对低频运动补偿的状态反馈控制,使高频运动分量不进入反馈回路,避免不必要的能源浪费和机械磨损。同传统的线性状态观测器相比,本设计方案不需要对船舶运动的数学模型进行近似的线性化处理。
仿真结果显示,同文献[4]相比,由于引入了增广状态变量和采用粒子群优化算法设计组合最优的观测器增益矩阵参数,观测器动态性能和估计精度得到明显改善。
4 结 论
针对船舶动力定位控制系统中的非线性状态观测器设计问题,提出了一种基于粒子群优化算法的增广无源状态观测器。以估计误差的低通滤波信号作为增广状态变量,通过在观测器方程中引入增广状态变量,以减少高频运动分量对低频运动参数估计的影响,在此基础上采用粒子群优化算法对观测器增益矩阵中的9个参数进行组合寻优,进一步提高观测器的动态性能。以一艘供给船为案例进行仿真分析,仿真结果表明所设计的增广无源观测器可以很好地滤除高频分量和噪声的干扰,从测量信息中准确估计出船舶低频运动的位移和速度分量。
参考文献
[1] 边信黔,付明玉,王元慧. 船舶动力定位[M].北京科学出版社,2011.
[2] FUNG P,GRIMBLE M J.Dynamic ship positioning using a self-tuning Kalman filter[J]. IEEE Transactions on Automatic Control,1983,28(3):339-350.
[3] FOSSEN T I,GROVLEN A. Nonlinear output feedback control of dynamically positioned ships using vectorial observer backstepping[J]. IEEE Transactions on Control Systems Technology,1998,6(1):121-128.
[4] FOSSEN T I,STRAND J P. Passive nonlinear observer design for ships using Lyapunov methods:full-scale experiments with a supply vessel[J]. Automatica,1999,35(3):3-16.
[5] 何黎明,田作華,施颂椒. 船舶动力定位系统的一增广非线性观测器设计[J]. 船舶工程,2003,25(4):47-49.
[6] 张相宜,杨宣访,王家林. 一种鲁棒的动力定位系统状态估计算法[J]. 计算技术与自动化,2017,36(3):6-11.
[7] 贾宝柱,谢灯峰,董秋军. 船舶动力定位系统非线性无源观测器的仿真[J]. 船舶工程,2018,40(1):198-201.
[8] 谢业海,徐慧璇. 基于PSO优化的船舶动力定位观测器[J]. 控制工程,2015,22(1):118-122.
[9] 薛彩霞,袁伟,俞孟蕻,等. 遗传粒子群优化算法在船舶动力定位控制中的应用[J]. 中国舰船研究,2016,11(4):111-115.
