基于数学核心素养直观想象下的正方体截面图形问题
2020-01-04贾立平
贾立平

【摘要】正方体是大家比较熟悉的几何图形,其截面(用一个平面去截几何体表面,此平面被几何体所截的部分)都有哪些图形呢?过已知不共线三点作几何体的截面问题比较抽象,把空间问题平面化是解决此类问题的常用手段.本文将详细地阐述确定截面图形的两种常用方法,希望对同学们了解截面图形、解决与截面有关的问题有所帮助.
【关键词】直观想象;正方体;截面;空间问题平面化
下面我们来看一道与截面有关的试题:
引例 正方体ABCD-A1B1C1D1中,E,F,G分别是AA1,BC,C1D1的中点,现有下列结论:(1)△EFG为正三角形;(2)异面直线A1G与C1F所成的角为60°;(3)AC∥面EFG.其中正确的结论的编号是( )
A.(1) B.(2)(3) C.(1)(2) D.(1)(3)
想要解答本题,我先来介绍一种学生较容易掌握的找截面的方法——交线法,仅供大家参考.
下面我们来了解一下做截面图形涉及的定理与性质:
1.两点确定一条直线,三个不共线的点组成一个平面.
2.只有在同一个平面的两条直线才可能相交.
3.如果一条直线上的两点在同一个平面内,那么这条直线上所有的点都在这个平面内.
4.如果两个不重合的平面有一个公共点,则两个平面的交线必定经过这个公共点.
交线法
运用该方法作图的关键在于确定截点(平面与几何体棱的交点),有了位于多面体同一表面上的两个截点即可连接成截线,从而得到截面.常见类型如下:
类型一:截面经过的三个点分别在多面体的棱上,且其中有两个点在同一个面的棱上.
例1 正方体ABCD-A1B1C1D1中,E,F,G分别在AB,BC,DD1上,求经过E,F,G三点的截面.
作法 (1)在底面AC内连接EF并延长,分别交DA,DC的延长线于点L,M;(2)在侧面DA1内连接GL,交AA1于K;(3)在侧面D1C内连接GM,交C1C于H;(4)连接KE,FH,则五边形KEFHG即为所求(如下图).
类型二:截面经过的三个已知点两两不在同一面的棱上.
例2 P,Q,R三点分别在直四棱柱AC1的棱CC1,A1D1,AB上,试画出过P,Q,R三点的截面.
作法 (1)先过P,R两点作辅助平面,过点R作R1R∥BB1,交A1B1于R1,则平面CRR1C1为所求辅助平面;
(2)在平面CRR1C1內延长R1C1,交RP的延长线于M;
(3)在平面A1B1C1D1内,连接MQ,交C1D1于点S,延长MQ交B1A1的延长线于点T;
(4)连接TR,交AA1于点N,延长TR交B1B的延长线于点K,再连接KP交BC于点L;
(5)连接RL,PS,QN,则多边形QNRLPS即为所求(如下图).
下面回到引例.
引例中(1)与(2)较容易判断,其中(1)正确,(2)错误.
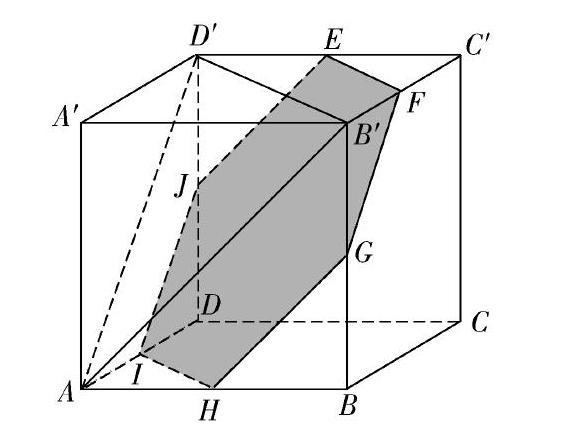
(3)为难点,面EFG截正方体的截面图形为六边形EIFKGJ ,如下图所示.作出这个截面图形并不是很容易,其截面类型同类型二,具体作法如下:
(1)取边A1B1 的中点R,连接GR,RB,CG ,得到矩形GRBC;
(2)在矩形GRBC内延长GF,与RB的延长线交于点W,则W∈面ABB1A1;
(3)连接EW,EW∩AB=I,WE的延长线交B1A1的延长线于点H;
(4)连接HG,HG∩A1D1=J,HG的延长线与B1C1的延长线交于点S;
(5)连接FS,FS∩CC1=K;
(6)连接GK,EJ,IF,则六边形JEIFKG即为所求的截面图形.
故(3)正确,本题答案为D.
除了以上常见的截面类型,还有截面经过的三个点中有一点或多点在多面体的面上的类型,方法同类型二,同学们可以自行研究,此处不再加以赘述.
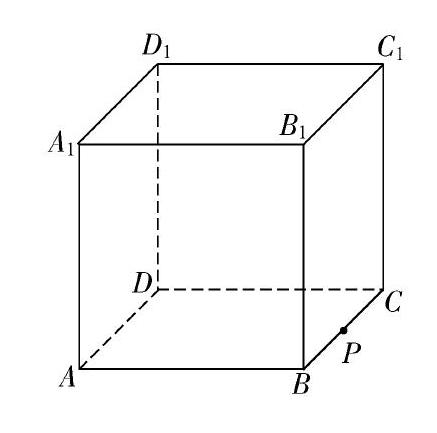
练一练1 (2013年安徽省理科数学试题第15题)如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点.过A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是(写出所有正确命题的编号).
(1)当0 (2)当CQ=12时,S为等腰梯形; (3)当CQ=34时,S与C1D1的交点R满足C1R=13; (4)当34 (5)当CQ=1时,S的面积为62. 解析 如下图所示. 答案 (1)(2)(3)(5). 练一练2 一个透明密闭的正方体容器中恰好盛有该容器一半容积的水,任意转动这个正方体,则水面在容器中的形状可以是:(1)三角形;(2)四边形;(3)五边形;(4)六边形.其中正确的结论是( ) A.(1)(3) B.(2)(4) C.(2)(3)(4)D.(1)(2)(3)(4) 解析 正方体容器中盛有容器一半容积的水,任意转动这个正方体,其水面总是过正方体的中心,所以这个题的本质就是过正方体中心的截面都可以是什么形状的.三角形、五边形的截面不过正方体的中心,故(1)(3)不正确;过正方体的一对相对的棱和中心可以做一截面,截面形状为长方形,故(2)正确;过正方体一面上相邻两边的中点和中心的截面为正六边形,故(4)正确.所以选择B. 练一练3 (2018年全国Ⅰ卷)已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为( ) A.334 B.233 C.324 D.32 已知正方体ABCD-A1B1C1D1 的棱长为1,点K在棱A1B1上运动,过A,C,K三点作正方体的截面,若K为A1B1的中点,则截面的面积为;若截面将正方体分成体积比为2∶1的两部分,则A1KKB1=. 解析 正方体下底面对角线AC与上底面对角线A1C1平行,K为A1B1的中点,取B1C1的中点K1,连接KK1,则KK1∥AC,连接K1C,则梯形ACK1K即为截面图形.根据正方体的棱长为1 ,易求得截面面积为98.易知当点K在棱A1B1上运动时,截面图形仍为梯形ACK1K,截面将正方体分成体积比为2∶1的两部分,则几何体KB1K1-ABC (棱台)的体积为正方体体积的13,设KB1=a,
