利用微元法将各类积分直接化成定积分

沙婵娟

【摘要】微元法是分析和解决积分问题的常用方法，它是采用“化零为整”的思想去解决问题.一般的积分都需要化成累次积分来计算，有时计算起来比较复杂，本文利用微元法简化了重积分和曲面积分的运算，即通过微元法寻找相应的微元，直接将二重积分、三重积分或者曲面积分化成定积分，而定积分计算相对来说简单，因此，利用此法可以更大地简化计算.

【关键词】微元法;重积分;曲面积分;积分微元

一、引言

微元法是积分学中非常重要的一种方法，在数学、物理和工程中被广泛应用.它一般要经过四个步骤：分割，取近似，求和，取极限.通常情况下，在使用微元法之前，我们会先对某事件做整体的观察，然后取出该事件的某一微小单元进行分析，通过对微元的数学分析和描述，最终解决整体，得到结果.合理有效地利用微元法的思想可以使原本复杂的问题变得简单易行.

在大学的公共基础课“高等数学”中，所有积分概念的提出都是通过微元法实现的.我们所得到的这些积分，包括重积分、曲线积分、曲面积分，都是基于定积分的概念，对积分区域进行扩展，得到新的一系列积分.对于这些积分的计算，先通过几何意义或物理意义化为二重积分或者三重积分，再化成累次积分的形式，最终得到极限值.实际上，很多问题我们可以根据积分中被积函数和积分区域的特点和相互关系适当地选择微元，将重积分和曲面积分直接化简为定积分，从而进行简单的计算.

二、各类积分直接转化成定积分

（一）重积分直接化成定积分

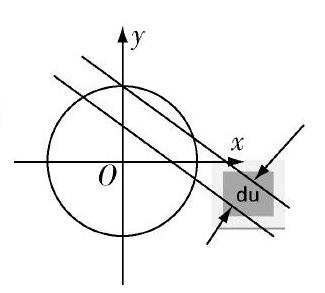
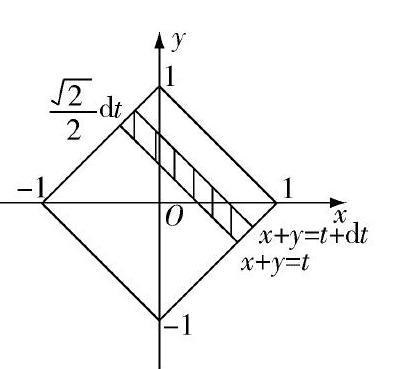
通常情况下，重积分是要根据积分区域的形状化成累次积分进行计算的，但是如果被积函数复杂，或者积分区域形状不规则，那么化成累次积分的过程就比较繁杂，或者化成累次积分后，计算量比较大.如果在重积分中，积分微元容易寻找或者容易表达，那么我们可以利用微元法直接找微元，化成定积分计算要容易得多.

下面通过三个例题介绍三种不同的类型.

经过上面三个例题的分析，有了最简洁的结果，我们在以后高等数学或者其他科目的学习中，便可以利用这些结论，在具体的题目中可以直接去计算重积分，省去了确定区域形状、选择合适坐标、化成累次积分这些繁杂的过程，而直接得到一个定积分，计算定积分即可，计算过程变得简单很多.

上面的几个例题中，积分区域都是用规则的直线或者平面进行分割的，得到的微元是长方形、带弧边的长方形或长方体，这种情况是我们容易碰到和掌握的.实际上，有些特殊问题，我们可以用不规则的曲线或者曲面进行分割.

我们看到，（2）的解答是非常简单的，大家可以试一下用我们常用的算法或者常用的分割方式去解决这个二重积分，还是有一定的难度的.而这种做法不仅可以用于二重积分的计算，还可用于三重积分的计算.

（二）曲面积分直接化成定积分

在高等数学的学习过程中，大部分学生对于曲面积分的计算掌握起来是有难度的，而我们会在这部分中研究曲面为旋转曲面的类型下，如何快速准确地得到曲面积分的值.

假设曲面是由曲线绕着z轴旋转所得，由旋转体的侧面积可知，旋转体的曲面面积微元dS=2πx1+dzdx2dz，则曲面积分就可以化简成定积分来计算.

这一部分我们主要对曲面积分直接化成定积分做了相应的分析，如果看到积分区域是旋转体，我们都可以用微元法分析其面积微元.

三、结束语

高等数学中积分的计算是一个重要的内容，不管是教学大纲、考研大纲，还是物理课程或者专业课程中，积分的计算必不可少.但是这部分内容对于学生而言又是个难点.在学习的过程中，我们要引导学生去理解积分的本质，清楚积分就是无穷多个无穷小的总和.它的结果我们可以认为是在单一维度下对某一个量的累加.

本文中的积分计算抛开教材中循规蹈矩的求解积分的方法，从微元法最本质的一点寻找积分微元，去化解积分，直接得到我们熟悉的、便于计算的一元函数的定积分.整个过程对学生对积分概念的理解和积分值的取得是有很大帮助的.这样的方法不仅适用于文中提到的几种积分模式，也适用于很多实际问题的求解.在实际问题中，我们只要可以找到简单的分割方式，順利找到对应微元，在分割区域上，便可以方便地把它化成我们熟知的定积分，对此大家可以继续进行探讨.

【参考文献】

[1] 同济大学数学系.高等数学[M].北京：高等教育出版社，2014：160-161.

[2] 唐燕贞.重积分、曲面积分直接化为定积分的一种方法[J].高等数学研究，2007（2）：10-11.

[3] 费时龙，孙善辉.计算三重积分的一种特殊方法[J].安庆师范学院学报（自然科学版），2013，19（1）：101-102.

[4] 张天德，蒋晓芸.高等数学习题精选精解[M].山东科学技术出版社，2017：341-345.