带水墙靶板对高速破片侵彻能力影响规律*
2020-01-02尤志锋郭驰名戈洪宇
陈 材,石 全,尤志锋,郭驰名,戈洪宇
(1. 陆军工程大学,河北 石家庄 050003;2. 中国白城兵器试验中心,吉林 白城 137001)
随着国际形势的发展,核武器的使用和研究受到了极大的限制,使得非核杀伤的大当量弹药在现代战争中的使用频率及发挥的作用越来越大,其产生的高速破片能够对人员和装备产生巨大的杀伤作用。目前,为了确实提高部队实战化水平,打赢高新技术条件下的现代战争,必须要求部队的作战训练更加贴近于实战[1]。因此,在装备战斗损伤试验中将越来越多的使用大当量成型弹药来进行装备打击试验。为使试验方案设计更为合理,就必须先对大当量成型弹药的毁伤威力进行分析。
破片毁伤参数是评定弹药毁伤威力的重要指标,其计算数据主要通过破碎性试验和飞散性试验来进行获取。破碎性试验的目的是回收弹药爆炸后的破片并按质量分组获取破片质量分布,飞散性试验的目的则是获取空间各个位置上破片的分布密度。针对小当量弹药,张志彪等[2]采用砂箱静爆法回收了变壁厚壳体膨胀破碎生成的自然破片,宋桂飞等[3]设计了一种新型爆炸容器装置来进行战斗部的回收,能够反复使用且有效回收爆炸试验后的破片,张玉令[4]采用长方形靶测试法对自制弹丸的破片空间分布情况进行了测量,毛亮等[5]通过布置环形靶的方式对可瞄准预制破片式战斗部的破片分布进行了分析,除此之外,在相关专业教材上也对破碎性试验和飞散性试验的方法进行了介绍和分析[6-8],这些研究主要是针对小当量弹药进行,对于大当量弹药的破片毁伤参数测量,虽有少数学者进行了研究,如王林等[9]通过改变靶板材料和布靶方式,对大当量杀伤战斗部的破片飞散特性试验方法进行了研究,但仍缺乏系统的试验标准规范。此外,现有的试验方法,均不能实现对大当量弹药破碎性试验和飞散性试验的同时实施,只能通过增加试验次数或提高对试验场地的要求来达到获取完整的破片毁伤参数的目的。然而,对于大当量成型弹药,其不仅造价高昂,同时毁伤威力巨大,试验次数的增加将大大提高试验成本和试验风险系数,而提高试验场地要求的方法则将大大降低试验效率。因此,探寻一种简单易行的大当量成型弹药破片毁伤参数试验新方法,对于降低试验费效比具有十分重要的现实意义,同时也能对大当量弹药毁伤参数测试试验方法的完善提供一定的思路。
本文中提出在靶板前方设置水墙的试验方法,实现对破片破碎性数据和飞散数据的同时获取。利用数值模拟的方式,分析破片打击带水墙防护靶板的侵彻规律,并分析水墙厚度和破片入射角度对破片侵彻能力的影响规律。在此基础上,通过实弹试验的方式,验证带水墙靶板收集大当量弹药高速破片的有效性。
1 试验原理
针对弹药破片的毁伤威力参数,通常采用静爆试验的方式来进行获取。如图1 所示,为某型弹药静爆试验场地布置示意图及现场图,通过在弹药一侧按照角度分布布置一定数量的金属靶板,在弹药爆炸后收集靶板上的穿孔及凹坑数量,则可得到相应飞散区间的破片数量,从而推算出弹药破片场的整体分布。对于大当量战斗部,例如航弹,其破片初速通常为2 000~2 500 m/s,因此在破片密度较大的距离内,破片几乎都能够穿透靶板,这就造成在一次试验中无法同时获取破片质量数据。因此,本文通过在靶板前方设置水墙的方式,旨在快速降低破片侵彻能力,弥补常规试验方法无法同时收集破片质量数据的缺陷,其示意图如图2 所示。
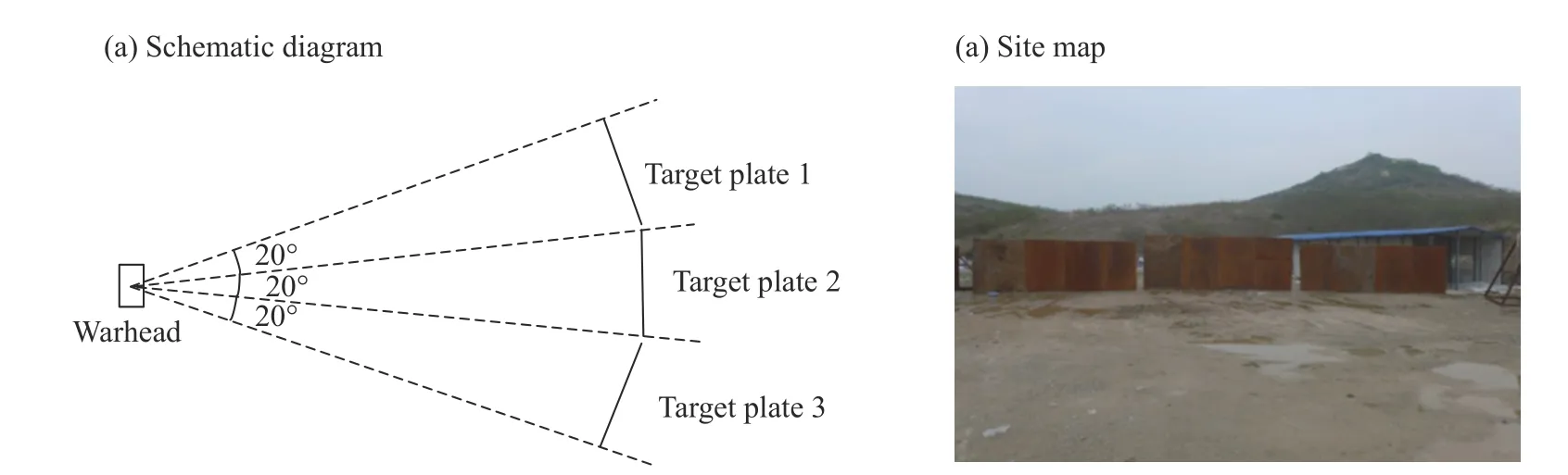
图1 静爆试验布置图Fig.1 Layout of static explosion test
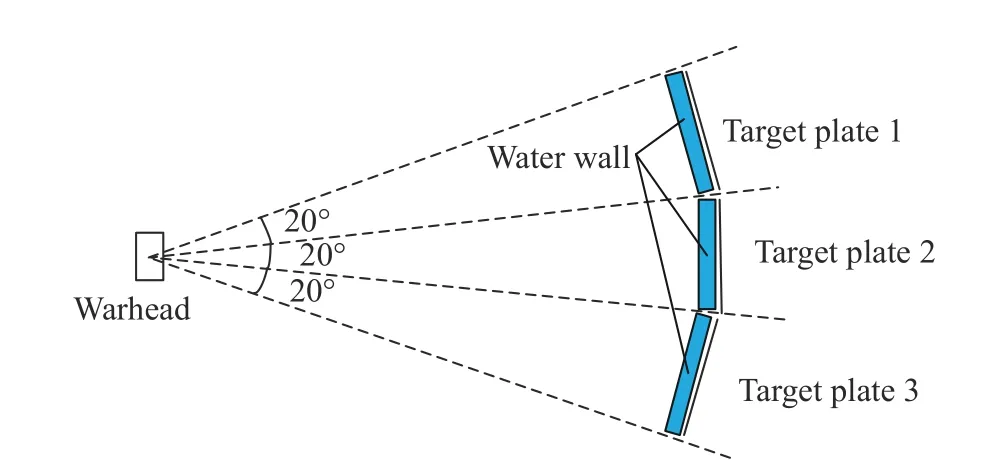
图2 水墙防护靶板示意图Fig.2 Schematic diagram of target plates with water walls
2 数值模拟模型
2.1 有限元模型的建立
利用有限元模拟软件AUTODYN 对高速破片侵彻带水墙靶板过程进行数值模拟。以方形破片为例,其尺寸为7 mm×7 mm×7 mm,质量约为3 g,进入水墙时初速为1 500 m/s;靶板厚度为3 mm,长宽尺寸为50 mm×50 mm,其四周设置为刚性固定,达到模拟试验场中靶板固定的效果。为了模拟破片在空气中飞行及穿越水墙的过程,在破片及靶板四周建立尺寸为100 mm×50 mm×50 mm 的空气域,并通过填充的方式将空气替换为水,由此建立靶板前方水墙的数值模型。破片和靶板均采用Lagrange 单元算法,空气和水采用Euler 单元算法,并在空气和水域边界处设置Flow-out 边界条件,实现空气和水域中边界能量的流出。所有模型单元网格大小均为1 mm。采用流固耦合算法定义破片与空气、水墙以及水墙与靶板之间的相互作用,通过侵蚀接触算法模拟破片侵彻靶板的过程。由于实际试验中水墙与靶板不能完全贴合,因此在水墙和靶板之间设置2 mm 的间隙。建立好的有限元模型如图3 所示。
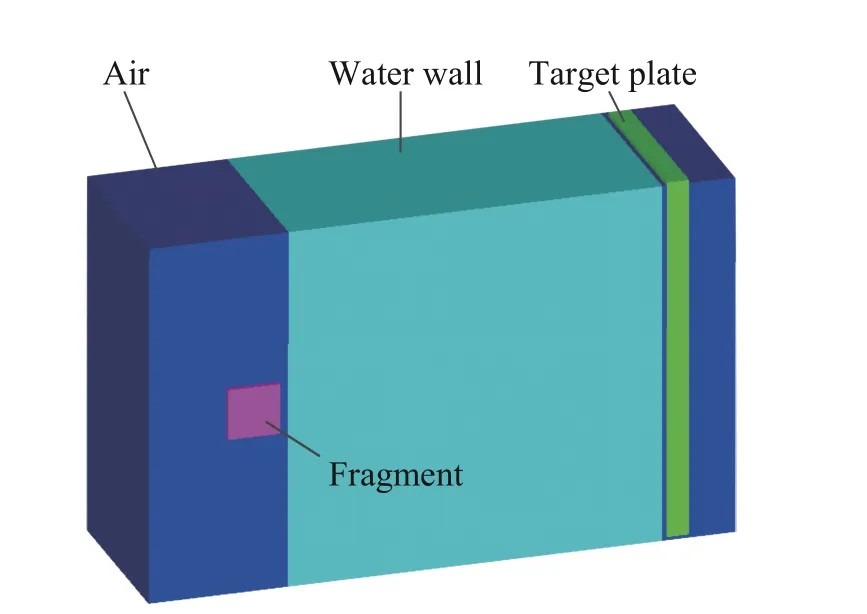
图3 有限元模型(1/2 模型)Fig.3 The finite element model (1/2 model)
2.2 材料模型的建立
2.2.1 破片及靶板材料模型
破片材料选用钨合金,靶板材料选用钢。使用Shock 状态方程和Johnson-Cook 强度模型来对两种材料进行描述。

表1 状态方程参数[10-11]Table 1 Parameters for equations of state[10-11]
Johnson-Cook 强度模型通常用于具有高应变率和承受高温的金属材料,该模型中其屈服应力Y由材料的应变、应变率和温度决定:



表2 强度模型参数[10-11]Table 2 Parameters for strength models[10-11]
2.2.2 空气及水的材料模型
采用理想气体状态方程对空气进行描述:
p1=(γ −1)ρae+pshift(3)
式中:p1为空气压力, ρa为空气初始密度,γ 为理想气体常数,e为比热力学能,pshift为压力偏移量。在空气模型中,取γ 为1.4, ρa为1.225 kg/m3,ea则取为206.8 J/g。
对水采用NULL 材料模型,其状态方程采用Grüneisen 状态方程[12]:
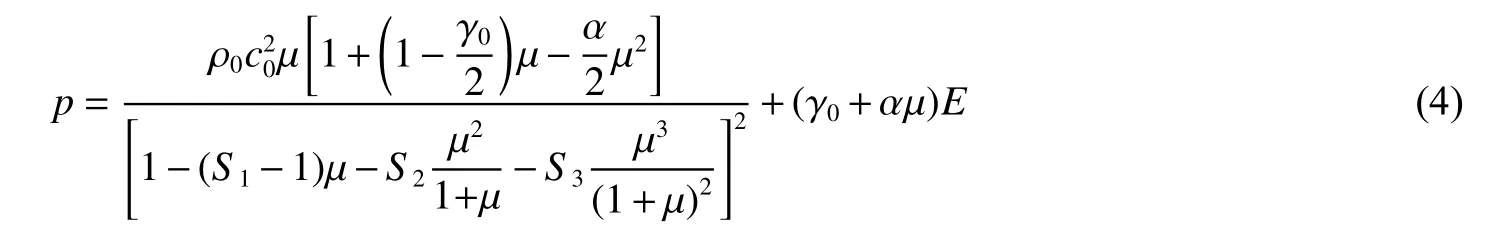
式中:p为压力,E为体积内能;c0为介质中初始声速,取为1 480 m/s;S1、S2、S3为冲击波输入参数,通常根据水介质的冲击试验数据确定,本文取S1=1.75,S2=0,S3=0;ρ0为常温下水的初始密度,ρ 为水当前密度;µ为介质压缩比,µ=ρ/ρ0−1;γ0为初始Grüneisen 系数,取为0.493 4;α 为Grüneisen 系数修正项。
3 数值模拟结果及分析
3.1 高速破片侵彻过程
对破片侵彻带水墙靶板的过程进行数值分析,得到破片不同侵彻状态信息如图4 所示,其中图4(a)~4(d)为水墙中冲击波压强云图,图4(e)~4(f)为金属材料内部应力云图。
由图4 可知,破片进入水墙的初始时刻,由于水的惯性压力,使得破片与水的接触区域产生巨大的压力,水墙中由于破片的冲击产生冲击波,冲击波随着破片的前进不断向前传播,并始终领先于破片。因此,冲击波首先与靶板接触,由于靶板的阻挡作用,冲击波在靶板表面产生反射,并与还未到达靶板的冲击波产生重叠,在交界面处产生更高的冲击波超压,在超压作用下,靶板产生一定的塑性变形,破片则是速度进一步下降。当破片穿透水墙后,继续以剩余速度对靶板进行侵彻,并最终穿透靶板。

图4 不同时刻破片侵彻带水墙靶板的典型状态Fig.4 Typical states of a fragment penetrating into a target plate with a water wall at different times
破片从初始时刻到穿透靶板的时间段内,记录其速度变化数据如图5 所示,同时记录破片侵彻无水墙防护靶板时速度变化数据如图6 所示。
由图5 可知,当靶板前方有水墙防护时,破片侵彻靶板分为2 个阶段:第1 个阶段为穿越水墙阶段,即高速破片在0~88 µs 时间段内对水墙进行了穿越,在此过程中,破片速度从1 500 m/s 下降至1 010 m/s,下降幅度为32.7%,其中在67~88 µs 过程中,由于冲击波在靶板作用下形成的反弹叠加作用,使得破片下降速率有所加大,但由于破片与冲击波接触面积较小,因此下降幅度不大;第2 个阶段为侵彻靶板阶段,即在88~120 µs 时,破片开始侵彻靶板,前期由于水墙的缓冲作用,破片在侵彻靶板过程中速度降低较为平缓,侵彻时间也持续较长,最终的剩余速度为599 m/s,相比初始速度下降幅度为60.1%。由图6可知,当靶板前方无水墙防护时,在0~68 µs 时间段内,破片在空气中飞行,其速度在此过程中几乎没有下降,在68 µs 时,破片与靶板接触并开始侵彻靶板,整个侵彻过程在83 µs 时结束,随后破片继续向前飞行,此时破片剩余速度为1 128 m/s,相比初始速度下降幅度为24.8%。因此由图5~6 可知,水墙对于高速破片的侵彻能力具有明显的降低作用,相比无水墙防护状态,速度能够多下降35.3%。
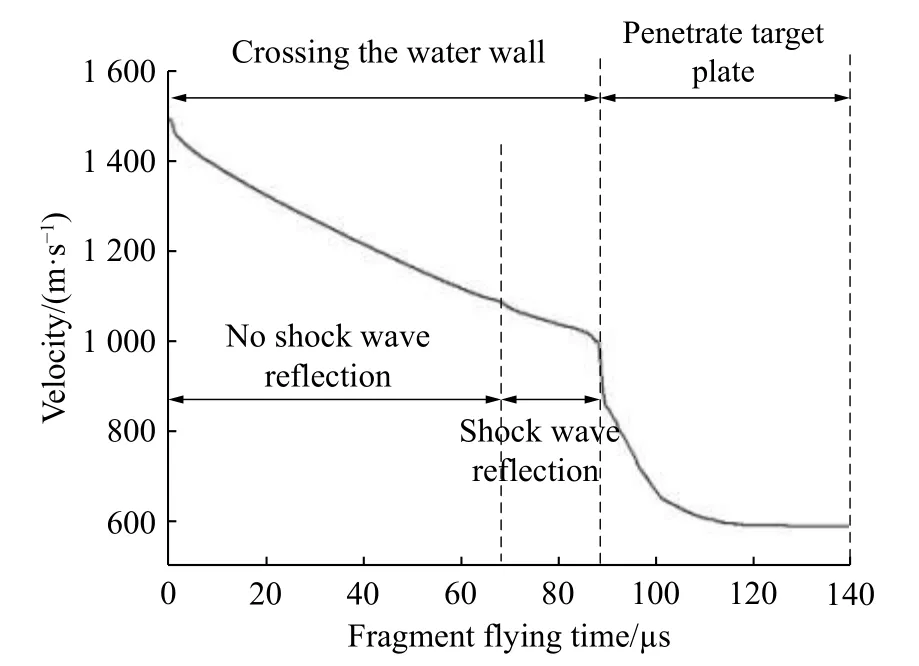
图5 破片侵彻带水墙靶板速度变化曲线Fig.5 Velocity-time curve of the fragment penetrating into the target plate with the water wall

图6 破片侵彻无水墙靶板速度变化曲线Fig.6 Velocity-time curve of the fragment penetrating into the target plate without the water wall
3.2 水墙厚度对高速破片侵彻能力的影响
设置水墙初始厚度为40 mm,按照每次增厚10 mm 的速度进行递增,对初速为1 500 m/s的破片侵彻具有不同厚度水墙防护的靶板过程进行数值模拟,得到破片剩余速度如图7 所示。
由图7 可知,破片侵彻带水墙防护靶板的剩余速度同靶板厚度呈线性关系,在破片质量、形状和靶板厚度不变的情况下,破片侵彻靶板的剩余速度随着水墙厚度的增大而降低,平均每增厚10 mm 水墙,破片速度下降约40 m/s。利用拟合曲线进行计算可得,当水墙厚度增大为287 mm时,破片的剩余速度可降低为零。因此,理论上当破片速度为1 500 m/s 时,对于3 mm 厚的靶板,只需在其前方设置厚度为287 mm 的水墙,即可实现对垂直入射的高速破片的拦截和收集。
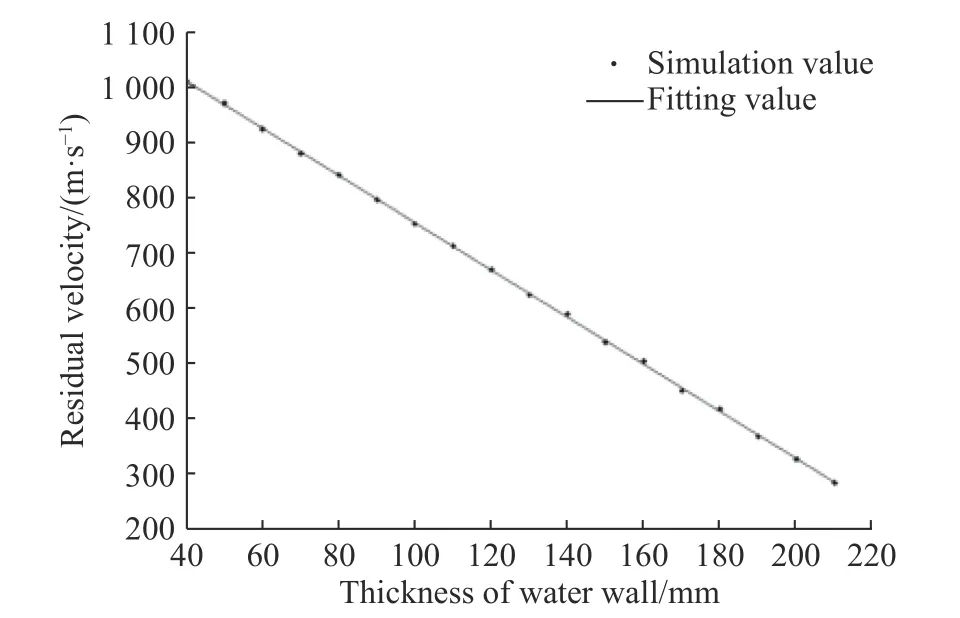
图7 破片的剩余速度Fig.7 Residual velocities of fragments
3.3 入射角度对高速破片侵彻能力的影响
设破片入射角为α,其值为破片入射方向同靶板平面法线之间夹角的大小,如图8 所示。
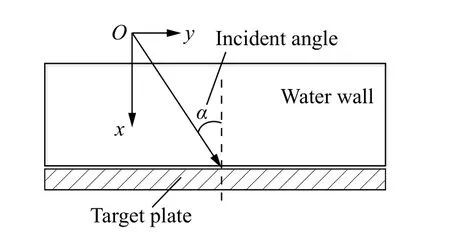
图8 入射角度示意图Fig.8 Schematic diagram of incident angle
在实际试验中,除部分破片能以α=0°的入射角对靶板进行侵彻外,其余破片的入射角α 均不为0°。因此,当高速破片速度为1 500 m/s,水墙厚度为50 mm,靶板厚度为3 mm 时,对破片以不同入射角度侵彻带水墙靶板的过程进行数值模拟,得到破片在与靶板作用后剩余速度绝对值的变化规律如图9 所示。
由图9 可知:当破片入射角度为0°~54°时,随着破片入射角度的增大,其穿透靶板后的剩余速度逐渐降低,即破片的侵彻能力逐渐降低,这主要是因为随着入射角度的增大,破片穿越水墙的实际距离逐渐增大,等效于破片垂直穿越时水墙厚度的增大,从而造成破片速度的降低;当破片入射角度为54°~58°时,破片速度降为0,此时破片处于嵌入未穿透靶板的状态;当入射角度大于58°后,破片速度又迅速升高,这是因为破片在x轴方向上的速度随着入射角度的加大逐渐降低,最终破片穿越水墙后在x方向上的剩余速度不足以穿透和嵌入靶板,而y方向上的速度仍然较高,从而在靶板表面产生跳飞现象,并继续朝着靶板周边飞散。由此可知,在进行实际试验时,对于不会产生跳飞现象的破片,只要达到能够收集垂直入射破片的条件,就能保证收集到非垂直入射的破片。而对于跳飞破片,其往往产生于入射角度较大时,虽然在实际试验中可通过调整弹药与靶板之间距离和角度进行避免,但为了保证试验的高精度,可对靶板进行适当改造,以实现对跳飞破片的拦截和收集。
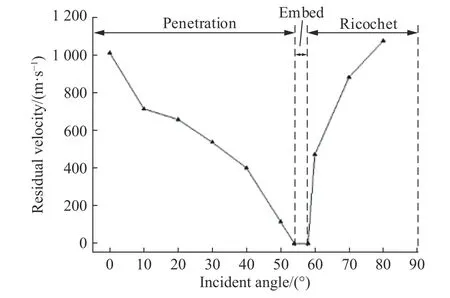
图9 破片剩余速度随入射角度的变化Fig.9 Variation of residual velocity of fragment with incident angle
4 试验验证
为验证带水墙靶板收集高速破片方法的有效性,在进行数值模拟的基础上,开展某型航弹破片采集试验。弹药等效TNT 装药质量约为124 kg,内部构造如图10 所示,其破片类型为方形预制破片,分别排布于装药顶部和尾部两端,呈轴对称分布,破片尺寸及材料与2.1 节数值模拟试验中的破片相同。由于破片分布的对称性,在实际试验中只需对一侧破片进行收集即可。
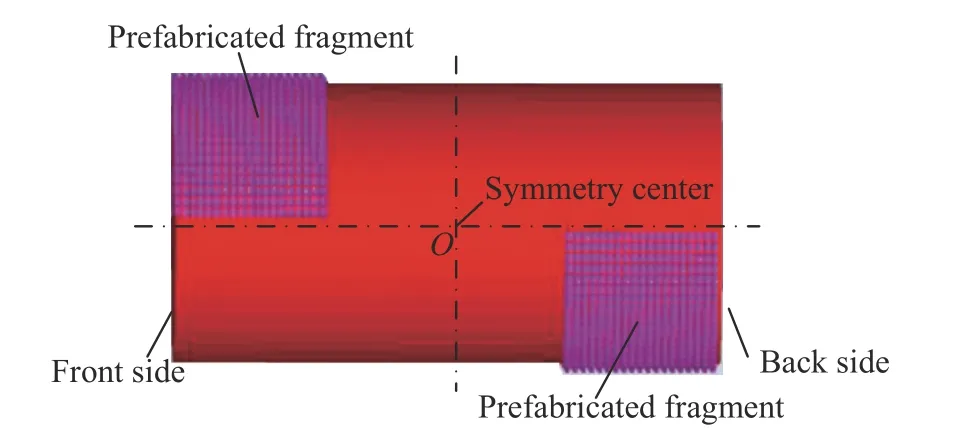
图10 弹药破片分布模型Fig.10 Distribution model of fragments
为使破片到达水墙时的速度同数值模拟模型中的入水速度相同,即达到约为1 500 m/s,首先利用金属丝网靶法对弹药爆炸后破片空中飞行速度衰减规律进行测算,试验示意图和现场图如图11 所示。在战斗部一侧布设3 组测速靶,3 组测速靶靶间间隔相同,设战斗部同靶1 之间间距为X1,靶间间距分别为X2、X3、X4。通过记录破片切断金属丝产生的电压脉冲信号,就可测得破片通过距离Xi(i=1, 2, 3, 4)时的时间ti(i=1, 2, 3, 4),以此便可求得破片空中飞行的速度衰减公式,具体计算过程见文献[8]。通过计算,可得到在距离弹药爆心20 m 处破片速度约为1 500 m/s。
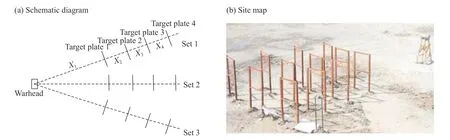
图11 测速靶的布设Fig.11 Layout of velocity measurement targets
又由3.2 节分析可知,为顺利收集到破片,需在靶板前方设置至少287 mm 厚的水墙,考虑以相应尺寸长方体容器盛水建立水墙难度较大,同时为了保证每枚破片在穿透水墙的过程中受其他破片影响较小,因此借鉴有限元计算思想[13],将单瓶矿泉水以交错累加的方式固定在靶板前方模拟水墙。单瓶矿泉水瓶身平均直径为62 mm,考虑矿泉水瓶之间间隙的影响,将矿泉水瓶交错叠加,共叠加10 层,从而保证每枚破片穿越的水墙厚度均大于等于287 mm。同时,靶板四周通过焊接的方式构造金属罩结构,将水墙进行包围,防止破片非垂直入射或在侵彻过程中轨迹发生变化,产生跳飞现象后向四周飞散而无法收集。通过以上分析,布置试验场地如图12 所示。靶板为3 mm 厚的钢板,长宽尺寸为4 m×3 m,通过刚性支架固定于地面。试验弹药通过木质支架进行固定,支架高度H为1.5 m,将弹药尾部一侧破片对准靶板中心,弹药中心与靶板表面垂直距离R为20.6 m,由三角函数关系可分别求得尾部破片中心同靶板长和宽的夹角β 和γ。

图12 破片收集试验现场布设Fig.12 Site layout for collection of fragments
弹药爆炸后,在矿泉水瓶中共收集到20 枚破片,如图13 所示,在靶板上及靶板周边区域收集到30 枚破片,靶板上无破片穿透后形成的破孔。设靶板面积为S,此时S即为半径为R的破片场在纬角β 和经角γ 内的球面面积SR的投影面积,通过求解球面面积SR,同时结合收集到的破片数量N,即可计算得到该区球面上破片的球面密度ρ,具体计算方法在文献[14]中有详细介绍,在此不再赘述。同时,对破片质量进行测量,可得50 枚破片质量分布如图14 所示,平均质量约为1.67 g。

图13 收集的部分破片Fig.13 Partial fragments collected
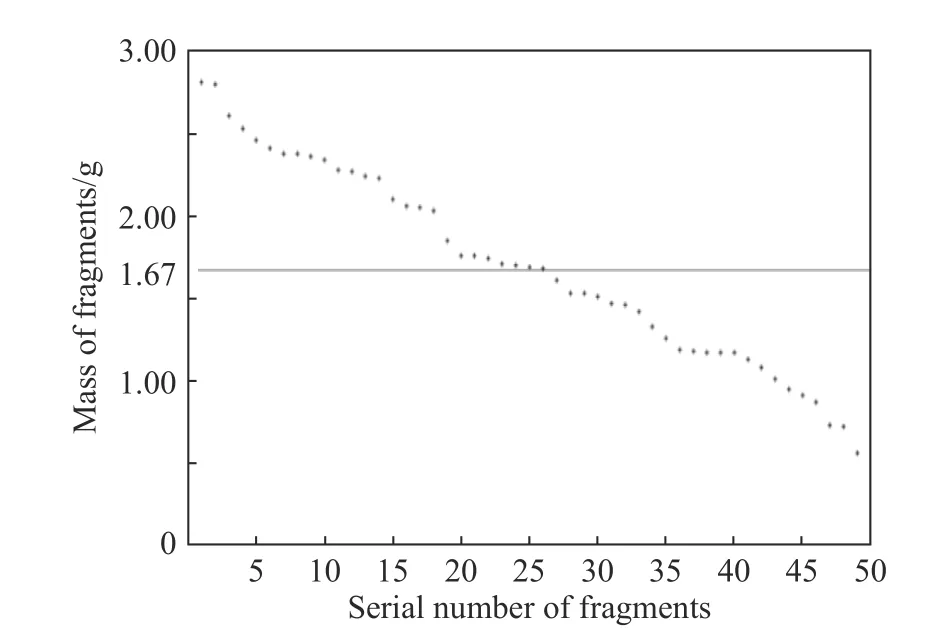
图14 破片质量统计Fig.14 Mass statistics of fragments
比较相同试验条件下无水墙靶板的试验情况如图15 所示,在一次试验中,由于破片穿透靶板,因此只能收集到破片场球面在靶板投影面积上的破片数目,以此求取对应区域球面上破片的球面密度,而无法同时获取破片破碎性数据,由此证明本文中提出的收集高速破片毁伤参数的试验方法是可行的。

图15 无水墙靶板试验情况Fig.15 Test situation of the target plate without a water wall
5 结 论
(1)通过在靶板前方设置水墙的方式,能够显著降低高速破片的侵彻能力,在相同模拟工况下,相比侵彻无水墙防护靶板情况,破片侵彻带水墙防护靶板后的剩余速度能够多下降35.3%。
(2)在相同模拟工况下,随着水墙厚度的增大,高速破片的侵彻能力逐渐下降,且下降幅度同水墙厚度呈线性关系。
(3)在相同工况下,随着破片入射角度的增大,高速破片的侵彻能力逐渐下降,当入射角度增大到一定程度时,破片还将产生嵌入和跳飞的现象,在实际试验中需针对此类现象做相应对策,避免所收集破片数据的不全面。
(4)通过实弹试验的方式,实现了对高速破片空间飞散数据和破碎性数据的同时收集,达到了减少大当量弹药爆炸次数的目的,验证了本文中所提出的利用带水墙靶板收集高速破片毁伤数据方法的正确性和有效性。
