溢流坝不同尾坎挑流消能数值模拟研究

马 强

（新疆玛纳斯河流域管理局，新疆 石河子 832000）

1 研究背景

随着计算流体力学的发展及计算机科学技术的发展，目前大多数学者都是通过数值模拟研究水力学问题，数值模拟相比物理模型而言模拟经济可靠、可重复性，尤其是在方案的比选上具有真实客观性。学者们针对溢流坝泄洪等水力学问题在不同方向上做了研究，如王强等［1］通过设计宽尾墩+阶梯溢流坝+消力池一体化消能工很好地解决我国单宽和高水头引起的巨大能量对下游河道及坝体产生的影响；李世城等［2］以物理模型为基础建立数学模型计算不同尾坎纵向坡度对消力池水流特性和消能率的影响，得出在实际工程中应综合考虑尾坎坡度和两边墙高度；郭观明等［3］通过设置导墙优化溢流坝的泄洪水流特性，结果表明直线圆弧组合导墙可有效改善直线导墙形成的不利流态，保证闸室泄洪水流的稳定；张勤等［4］为研究阶梯溢流坝首级阶梯的角度对坝面掺气得影响，通过6种水工模型试验得出首级台阶面角度为10°最优的方案。

本文通过建立两种不同的尾坎形式溢流坝数学模型进行研究，进而分析研究其不同尾坎形式对泄洪消能的水流条件的影响变化，为类似工程建设和研究提供理论基础。

2 数学模型

通过FLOW-3D计算软件对此模型进行三维模拟，对于水流的模拟，选择RNG- k -ε模型［5］。

本计算模型网格划分采用结构化矩形网格将整个计算模型进行划分，每个单元网格边长为0.5m，网格总数量300万。

2.1 控制方程

以数值模拟的准确性计算模拟选取较为关键，主要是通过模型方程组迭代计算将较为复杂的水流流态以图形和数据的形式反映出来。

连续方程如式（1）：

式中 ui为三维坐标轴上流速分矢量 （m/s）；Ai为三维坐标轴上的流体的分面积分数；xi为x坐标轴方向。

动量方程如式（2）：

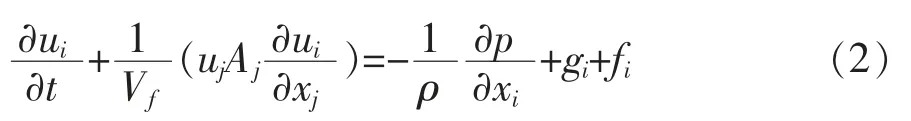
式中 t为时间（s）；Vf为三维流体的体积分数；Uj为y坐标轴上的分速度 （m/s）；Aj为y坐标轴上的面积分数；xj为y坐标轴方向；ρ为该流体密度 （g/cm3）；p为在流体上的作用压力（Pa）；gi为三维坐标轴上的流体的重力加速度 （m/s2）；fi为三维坐标轴上的流体的黏滞力（Pa）。

紊动能k方程如式（3）：

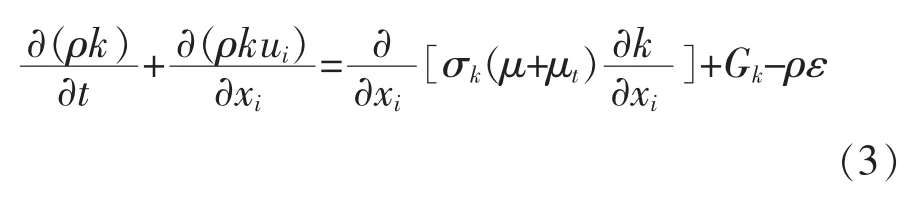
式中 k为流体紊动能 （kg·m2/s2）；σk=1.39 （经验系数）；μ为流体动力黏滞系数 （Pa·s）；μt为紊动黏滞系数；Gk由速度梯度引起的紊动能产生项

2.2 边界及初始条件设置

溢流坝上游河道设置流量控制边界，溢流坝下游河道设自由出流边界，整个水工模型正上方设置大气压力边界，模型其他位置设置固体边界。根据预定值溢流坝上游初始水位105m，模型溢流坝下游河道初始水位为30m；整个模型的模拟过程给定流量Q=1140m3/s。

2.3 模型验证

为研究溢流坝不同尾坎对挑流消能的影响，通过建立数学模型进行全真模拟，以红山嘴引水工程中的泄洪溢流坝为验证对象，该工程引水枢纽洪水标准30年一遇，洪峰流量1140m3/s，校核洪水标准100年一遇，洪峰流量1760m3/s。 进水闸设计流量105m3/s，加大流量140m3/s，泄洪冲沙闸设计流量420m3/s，校核流量560m3/s，泄洪闸设计流量400m3/s，校核流量487m3/s，滥流堰在河道来流量1140m3/s时开始溢流。 由于计算机的计算能力和模型建立的准确性都对模拟产生影响，为此将数值模拟的结果和物理试验的结果进行验证，如表1，图1。

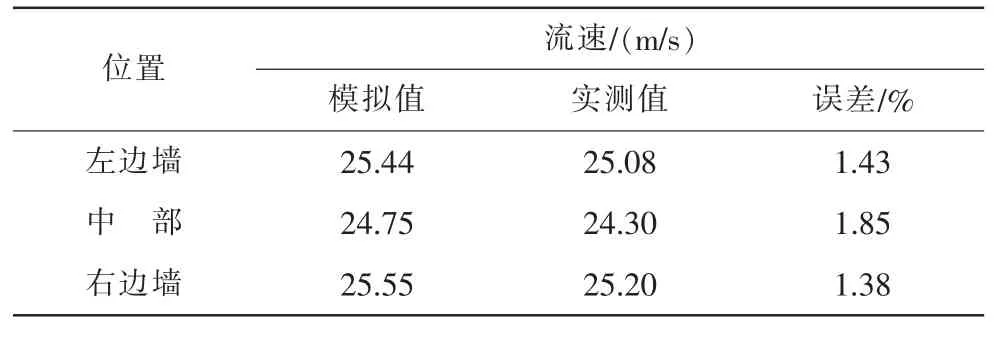
表1 溢流坝尾坎平均流速

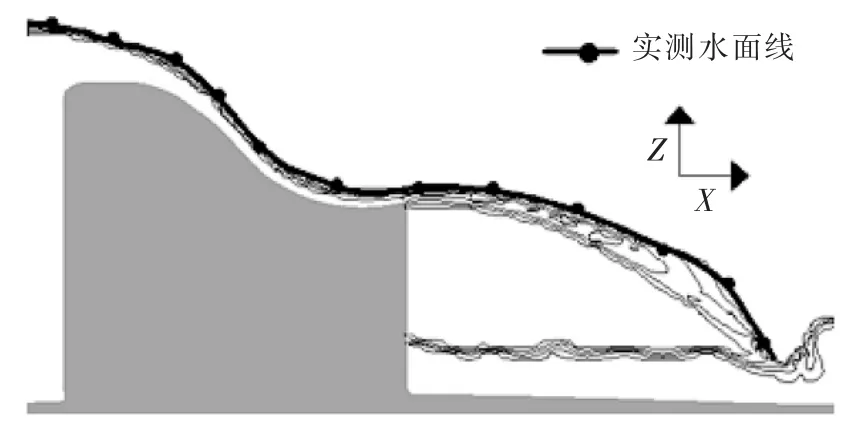
图1 挑流水面线

本次计算通过测量取其平均数，将溢流坝堰顶实测平均流速与数值模拟结果比较分析，当Q=1140m3/s时溢流坝挑流尾坎平均流速，结果表明两者相对误差较小，误差在1.38%～1.85%之间。

由图1可知，将溢流坝挑流水面线的实测点通过Tecplot软件绘制数值模拟云图，结果表明相比实测的水面线与数值模拟的结果相吻合，验证水面线在挑流面和入水流态和形状一致，表明几何和数学模型相对较准确。本文计算模型建立准确可靠，可为不同尾坎的溢流坝挑流消能的影响进行研究。

3 不同尾坎溢流坝数值模拟

溢流坝的尾坎形式多种多样，不同尾坎形式对挑流消能的影响不同，为准确研究不同尾坎溢流坝挑流消能挑流产生的影响，通过数学软件模拟分析不同尾坎溢流坝挑流水舌、水流流速、挑流效能率，得出同等流量下两种尾坎溢流坝挑流消能的差异性及方案比较，具体建模如图2。

图2 溢流坝模型

3.1 模拟结果及分析

3.1.1 水舌挑距

由于水流受不同的挑流尾坎的影响，其水流形式及能量也在发生变化，为了研究差动式和连续式尾坎在溢流坝挑流中产生的差异性变化，根据数值模拟结果整理如图3。

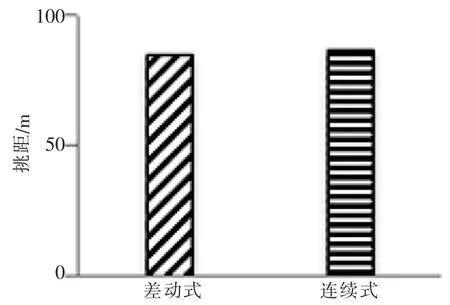
图3 挑距

由图3可知，差动式尾溢流坝的挑距比连续式尾坎挑距近，究其原因水流在溢流坝上发生挑射主要依靠巨大的水动能，在同样的水动能情况下由于水流在溢流坝尾坎处受差动式的挑坎影响较强，部分水流发生碰撞交汇导致能量有所减少，从而导致挑距相对较近，但整体上两种尾坎挑距都相对远离坝体在安全范围内，对大坝坝址稳定和安全影响较小。

3.1.2 流速

水流在差动式尾坎和连续式尾坎上的不同形式的碰撞和交汇，都对挑流的流速影响不同，为研究两则之间的差别和影响，通过FLOW-3D软件模拟进行分析得到流速等值线图，如图4。

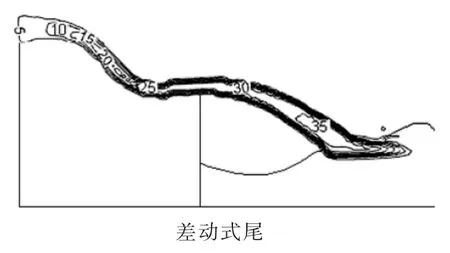
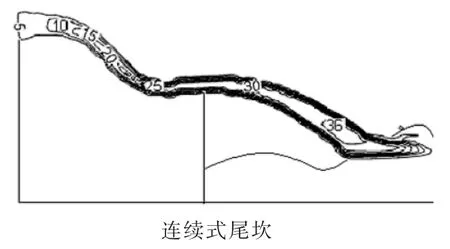
图4 挑流流速等值线

由图4可知，沿溢流坝水流方向，流速随着挑射的距离增加也在增加，最小流速在溢流坝堰顶处为5m/s；差动式最大流速35m/s，连续式最大流速36m/s，但两种尾坎挑流最大流速都在挑流水舌入水处。

3.1.3 消能率

由于溢流坝挑流消能率的计算方式各有不同，本文的溢流坝挑流消能的消能率η 采用通用的消能率计算公式，如式（4）：

式中 E1，E2分别为上下游断面总能量（m），E1=H1+其中H，H为上下游计算断面的水12深 （m）；v1，v2为上下游计算断面的平均流速（m/s）；α1，α2为上下游进出口断面流速系数，取1［6］。

经计算，差动式尾坎的消能率比连续式尾坎消能率高4.35%，如表2。

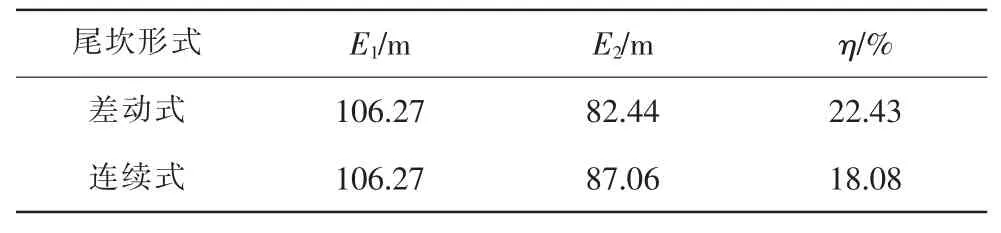
表2 挑流消能率

由于溢流坝挑流时水流在坝面发生碰撞，相比连续式尾坎而言差动式尾坎这种碰撞较强，因此对于同种流量采用差动式尾坎溢流坝挑流消能的效果较好，对下游河道及两岸边坡影响较小。

4 结语

（1）通过模型验证以可知，FLOW-3D软件中RNG-k模型模拟水力学中水气二相流问题较好，可重复性高。

（2）由于水流在溢流坝尾坎处受差动式的尾坎影响，部分水流发生碰撞交汇导致能量有所减少，从而导致挑距相对较近； 沿溢流坝水流方向随着挑射的距离增加流速也在增加，下游河道差动式最大流速比连续式最大流速小。

（3）差动式尾坎比连续式尾坎发生碰撞较强，因此对于同种流量采用差动式尾坎溢流坝挑流消能效果较好，对下游河道及两岸边坡影响较小。