应用EDM原理对衡水市水资源时间序列预测分析
2020-01-01王超
王 超
(河北省石家庄水文水资源勘测局,石家庄 050051)
水资源预测是区域水资源规划管理的基础,受气候变化密切影响,水资源表现出时间波动性与突变性,这给预测研究带来一定挑战。本文基于时间序列数据集的新型建模方案 (empirical dynamic modelling,EDM),阐述模型原理与建模过程,为水资源预测开拓新思路。
1 EDM原理与数据处理
经验动态模型 (empirical dynamic modelling,EDM)是针对时间序列环境变量的动态建模分析方法,该方法扩展了传统的复杂矩阵中定义为平衡系统到动态系统过程中处于平衡状态[1-2]。 传统雅克比矩阵是一个线性化方程组,矩阵之间部矢量交互通常是安装一定模式设计的固定系数。 然而在实际生态系统中几乎不存在静态平衡,更为普遍的是表现为非线性行为。 EDM框架强调系统状态随生态系统向量状态的变化而变化,并具有时间动态序列特征。EDM的内涵丰富,主要包含非线性动力学识别、CCM动态归因、生态序列预测等内容。
本文主要应用EDM原理中的S-map和CCM算法进行论述。
1.1 S-map算法
S-map是基于时间滞后信息的一种系统动力学回归模型,其框架如式(1):

S-map通过线性逼近已经完成在对引子流形上的每个局部位置x(t*)的权重设计[3]。 在吸引子流形上,对于更接近目标点x(t*)的向量,权重更大,其中参数k是权重的控制参数之一,d为平均距离,权重计算如式(2):

1.2 CCM算法
交叉收敛映射CCM (Convergent Cross Mapping,CCM)算法是EDM框架的重要内容之一,由Sugihara等[4]于2012年在《Science》上公开发表的新型因果关系检测方法。 区别于格兰杰等因果关系检验的互相关函数与信息熵传递内核。 CCM是基于Takens嵌入定理,Mx和My是同胚胎中M中的影子流形,它们均是通过对原始序列x,y的时滞信息重构得到的,由此产生了Mx与My之间的连续映射,若Mx对My有因果关系,则能够在My上找到Mx的过程标签。 对于n维系统M中关联变量Mx,My,构建影子流形如式(3):

式中 E为嵌入维数;τ为时滞步长。
若在Mx上找到系列与My,k0对应的流形,My,k0流形平均距离函数如式(4)~式(5):
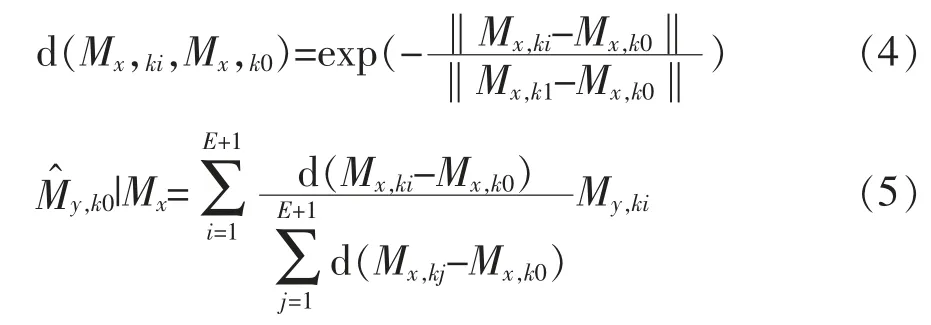
式中 k为时间序列集的长度,i,j∈k。
若Mx在My上的映射收敛到0~1之间,表明Mx是My的归因。
1.3 数据处理
通过《河北年鉴》中提取衡水市水资源总量年值(1970~2018年),并以此作为目标变量进行预测分析。水资源总量(WR)的变化与气候变化密切相关,通过文献分析[4-5],选择若干高频变量作为预测因子,分别是年降雨量 (Pre)、 年平均温度 (Tem)、 湿度(Mois)、日照时数(Hour)、蒸发量(ET),气象因子数据来源于中国气象中心,运用R语言实现水资源的预测分析研究。
2 结果与分析
2.1 基于S-map的非线性动力学
EDM方法的应用性具有严格标准,不仅要求数据集为连续性的时间序列变量,还要求事物本身符合动力学特征。 rEDM开源程序包中设计了相关检测程序,通过S-map算法中的权重参数k进行迭代,对比不同迭代结果中预测值与实际值的相关系数(rEDM中规定相关系数用rho标识)。 当k为0时,状态系统中吸引子流形各点的权重相同,此时的S-map算法简化为标准的线性模型,当k大于0时,则为非线性预测模型。 如图1(b),rho在k大于0时的值均高于k为0时rho的值,说明线性动力学的存在,即运用EDM原理建立衡水市水资源总量的动态模型具有良好的适用性。另外,时滞步长表征了非线性预测的长度,如图1(a),当步长为5时,rho达到最高水平,因此在后续的预测中选定该参数为5。

图1 非线性动力学识别
2.2 相关参数设定
嵌入维数定义为重构吸引子流形所需的变量维数,其不仅仅所指预测变量个数,包含相关变量的时滞子集,如图2,图中横坐标为嵌入维数大小(E),纵坐标为基于S-map 的预测值与实际值的相关系数rho,rho越大,说明嵌入维数最优。 其中在WR,Pre两变量中,最佳嵌入维数为8和2;在WR和Tem组合中最优值为8和4;Mois在最佳嵌入维数为4;Hour和ET则均为7。 嵌入维数的大小决定模型的复杂程度,若其值过大,则会导致状态空间过密和信息重叠,并损失动力结构性规律; 反之过小则产生状态空间依赖性不足,预测精度较低。 通过rEDM程序号中的simplex函数可给出最佳嵌入维数的平衡选择。
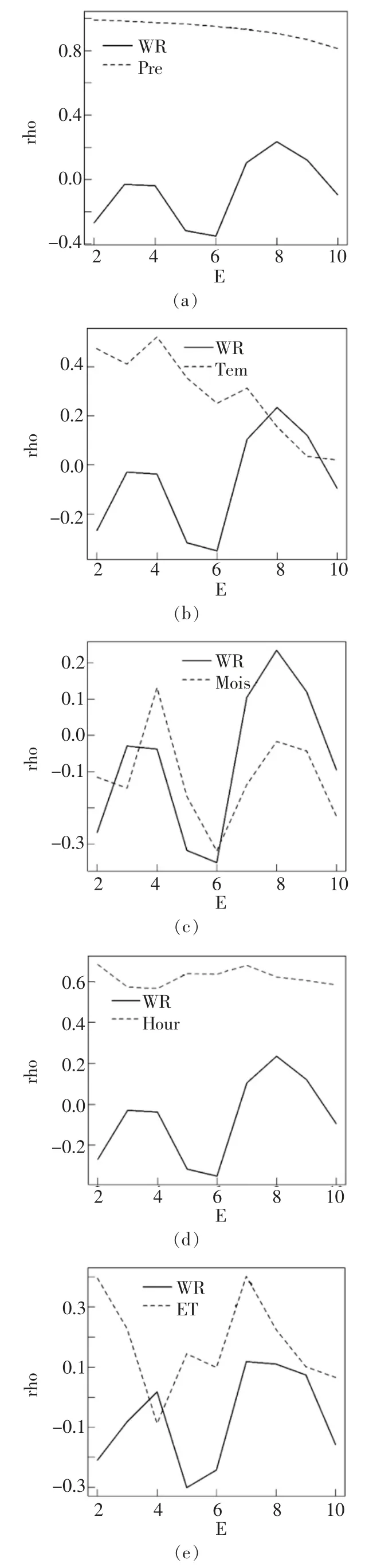
图2 嵌入维数选择
2.3 基于CCM的水资源变化归因
经参数优化后运用rEDM中的CCM_test函数对衡水市水资源总量WR与气候环境因子之间的归因识别。 如图3,图中横坐标为时间序列数据集的时间变化; 纵坐标为各单变量通过时滞构建吸引子流形后的点值与原来点值的相关性系数。
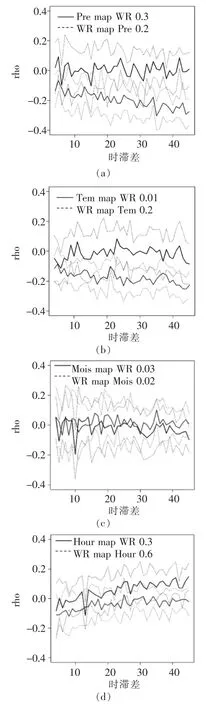

图3 基于CCM的双变量动态交互
图3(a)中Pre在WR上的投影系数值为0.3,WR在Pre上的投影系数为0.2,均介于0~0.5,表明二者互为动力学因果关系,即降水量是水资源量的因,同时水资源量也是降水量的因,说明二者互为影响。 其中Tem map WR 0.01,说明温度的变化是区域水资源变化的显著性成因(P<0.05);同时水资源量的变化也会引起温度的变化(WR map Tem 0.2),但这一过程并不显著。 大气湿度与水资源量之间互为成因,其中湿度对水资源量的投影值(Mois map WR)为0.03;水资源量对湿度的投影值(WR map Mois)为0.02;归因均达到显著水平。 日照时数对水资源量具有一定影响 (Hour map WR 0.3),前者是引起后者变化的原因;而后者不会引起前者的变化(WR map Hour 0.6,P>0.5)。 图3(e)中ET与WR交叉收敛特征十分明显,二者互相投影值分别为0.01,0.02;通过5%水平信度检验,说明蒸发变化是衡水市水资源量变化的显著性原因;同时后者也是前者的成因。
2.4 基于multuview的水资源预测
rEDM程序中基于EDM原理设计了图4中非线性动力学预测方法,分别是Simplex、S-map、multivariate、multi-view等,Chun-Wei Chang等[6]研究表明以multiview的预测效果最佳,因此本文选择该方法对1971~2018年衡水市水资源总量变化进行时间性预测,结果如图4。
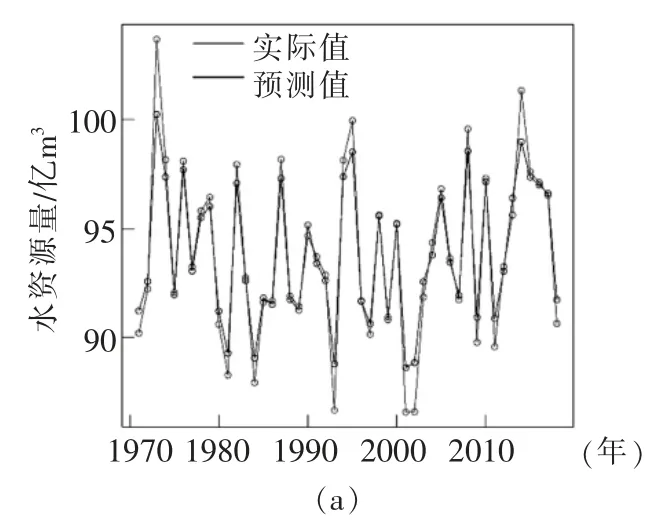

图4 基于multi-view的衡水市水资源总量预测
从图4(a)可知,multi-view模拟的水资源总量年值能够较好地拟合其实际变化,虽然有误差存在,但均较小;依据图4(b)可知,实际值与预测值之间的相关系数高度0.95,Mae和RMSE为0.71亿,1.01亿m3,表明预测精度较高,预测结果可靠。
3 结语
(1)水资源是气候系统耗散过程中的矢量之一,水资源的时空变化与气候变化密切相关,通过建立气候因子与水资源总量之间的关系模型能够较好地开展水资源预测。
(2)介绍了应用EDM原理对衡水市水资源进行预测的实证方案,建模过程表明水资源时序变化更加符合非线性特征,相对于传统线性模型,EDM模型具有一定的适用性;EDM框架中的CCM算法检测出了该市水资源变化的成因,从投影值来看,蒸发与温度的影响其显著成因(P<0.05),虽然大气湿度、降水量、日照时数对其具有一定影响,但并不显著。
