让习题讲解充满数学思考和空间想象

谢爱进

[摘要]在習题讲解过程中，教师若能根据学生的具体情况，针对不同的知识点，有组织、有意识、有目的地引导其进行数学思考和空间想象，使学生养成勤于思考、善于分析、归纳总结的良好习惯，长此以往，学生的学习兴趣、学习信心、认知水平、解决问题的能力将会大大提升。

[关键词]习题讲解;数学思考;空间想象

[中图分类号]G623.5 [文献标识码]A [文章编号]

1007—9068（2019）32—0042—02

在小学数学教学中，经常会出现一些在求知指导的过程中出现的规律（称之为“中间规律”），以及解题之后，通过对结论的再开发、再引申、再归纳得到的规律（称之为“题后规律”）。在平时的数学习题讲解过程中，教师可能会因为赶时间、赶进度而就题讲题，只要学生理解了、会算了就以为达到目的了，忽视某些习题在演变过程中出现的一些规律以及对结论的归纳小结。对此，教师应适时对教学进行调整，让学生经历计算过程，依据算式特点去发现、归纳其中隐含的规律，只要教师做细、做到位，将会极大地提高学生的学习兴趣，增强学生学好数学的信心，激发学生的求知欲，提高学生快速解决问题的能力，为学生今后的学习打下坚实的基础。

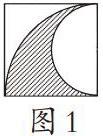
【案例1】图1中正方形的边长是6厘米，求涂色部分的面积。

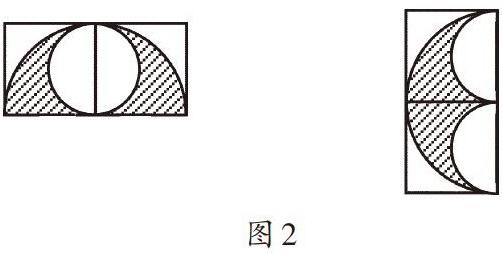
教师通常这样帮助学生分析：看图分析题意，得出解题思路是“用连同空白半圆在内的大扇形的面积减去空白半圆的面积，就得到图中阴影部分的面积”。具体计算过程为：第一步先算大扇形的面积，3.14×6²÷4=28.26（平方厘米）;第二步再算出空白半圆的面积：3.14×（6÷2）²÷2=14.13（平方厘米）;第三步求出两部分的面积差，28.26-14.13=14.13（平方厘米），从而求出答案。部分学生在教师的分析指导下很快就理解和掌握了，对于做错的学生，教师让其直接订正。看似省时高效，但是笔者认为，如果教师能引领学生利用轴对称的知识，将图形逐步还原，就可通过观察、比较、计算、归纳，发现空白半圆的面积与阴影部分面积之间的关系。将例题图形沿着正方形的右边或下边为对称轴还原图形，得到如下两图形（如图2）：

它们阴影部分的面积计算为：3.14×6²÷2-3.14×（6÷2）²=56.52-28.26=28.26（平方厘米）。在此基础上再次以半圆的直径为对称轴还原，图形变化为图3：

阴影部分的面积计算为3.14×6²-3.14×（6÷2）²×2=113.04-56.52=56.52（平方厘米）。再联系例题阴影部分面积可综合列式计算为3.14×6²÷4-3.14×（6÷2）²÷2=28.26-14.13=14.13（平方厘米）。

在引导学生计算时，教师有意识地用彩色粉笔画出上面三道算式中下划线部分的等式，引导学生观察、比较算式中各部分的含义，学生经过充分的观察与交流，肯定能发现每种情况中的阴影部分的面积与空白部分的面积是相等的。故今后遇到与例题相类似的题目，学生可通过直接计算半圆的面积得到阴影部分的面积。在帮助学生分析求解的过程中，教师要站在教材的高度，从题目演变过程的角度，及时引导学生归纳发现一些“中间规律”，让习题讲解充满数学思考和空间想象，从而激发学生的学习兴趣和求知欲，提高其解决问题的能力。

【案例2】三块边长都是12厘米的正方形铁皮，分别按图4的（1）（2）（3）剪下不同规格的图片，它们剩下的铁皮面积相等吗？

根据条件“三块边长都是12厘米的正方形铁皮”，可知图中三个正方形的面积相等，要求三个图中剩下的铁皮面积的关系，首先看三个图中阴影部分的面积关系，然后再去分析剩下的铁皮面积的关系。教师先组织学生分别计算阴影部分的面积。

图（1）阴影部分面积为π×（12÷2）²=36π（平方厘米）;

图（2）阴影部分面积为π×（12÷2÷2）²×4=36π（平方厘米）;

图（3）阴影部分面积为π×（12÷3÷2）²×9=36π（平方厘米）

通过计算后，学生不难发现：三个图中阴影部分的面积相等，所以每个图形中剩下的铁皮面积也相等。笔者以为，解题至此，还应拓展：在同样的正方形铁皮里剪16个、25个（如图5）……两两相切且面积相等的最大的圆，每个正方形中所有圆的面积和与例题中阴影部分的面积相等吗？

教师放手让学生通过小组合作，选择计算“剪16个、25个……两两相切且面积相等的最大圆”中的一种情况，求出阴影部分的面积。学生通过展示汇报，共同检查每种情况下的列式和计算结果是否正确，然后把算式与结果写到黑板上（与例题对应的写位置上），如剪16个圆的面积和为π×（12÷4÷2）²×16=36π（平方厘米），剪25个圆的面积和为π×（12÷5÷2）²×25=36π（平方厘米）……学生通过观察、比较、讨论、归纳，得到统一的结论：在相同的正方形铁皮中剪下1个、4个、9个、16个、25个……两两相切且面积相等的最大的圆，每个图形中所有圆的面积总和相等，所以每个图形中剩下的铁皮面积也相等。经验丰富的教师还有可能会提问：假如在这样的正方形中剪下一个最大的扇形（如图6），这个扇形的面积还与上面图形中阴影部分的面积相等吗？

学生再次通过计算得出π×12²÷4=36π（平方厘米），同样得到“相等”的结论。像这样解题之后，根据题意，对结论进行再开发、再引申、再归纳，可拓展学生思维，帮助学生系统建构知识、理解知识、运用知识，让习题讲解充满数学思考和空间想象，激发学生的学习兴趣和求知欲，提高学生解决问题的能力。

在平时的教学工作中，遇到类似的情况时，教师应多站在学生发展的角度，站在教材设计意图的角度，站在知识点内在联系的角度，让习题讲解充满数学思考和空间想象，以引领学生积极主动地针对不同习题的变化与引申，学会数学思考，并通过不断总结，发现知识隐含的规律，培养数学思维，不断提高解决问题的能力，这也是培养学生数学核心素养的重要组成部分，符合学生终身学习和自我发展的需要。

（责编 罗艳）