基于指令滤波的电液伺服系统输出反馈控制
2019-12-31王广文姚建勇
王广文,姚建勇
(南京理工大学 机械工程学院,南京 210094)
电液伺服系统具有动态响应快、输出功率大、体积小以及控制精确度高等优点,在工业生产、国防以及航空航天等领域得到了广泛的应用.电液伺服系统本身具有较强的非线性特性,如摩擦非线性,电液伺服阀流量压力非线性等问题.此外,电液伺服阀的流量增益、泄漏系数、外负载质量以及外部干扰、未建模动态、输入饱和等具有建模不确定性[1-2],这些问题为控制器的设计带来了较大困难,并限制了电液伺服系统高性能控制器的发展.
近年来,为了提高非线性系统的控制性能,国内外学者做了大量研究.文献[3]利用反步方法来控制非线性系统,文献[4-6]分别将滑模、自适应及自适应鲁棒方法应用于液压系统的控制中,在处理系统未知参数及减弱干扰方面取得了较好的效果,在很大程度上提高了控制器的性能.然而,实际的液压系统还存在系统状态不可测问题.文献[9-11]引入一种基于扩张状态观测器的输出反馈控制算法对系统的状态进行估计,同时保证了系统的稳定性.在液压系统中,反步控制方法应用广泛,但传统反步控制方法存在“微分爆炸”问题,需要在每一步的设计中对虚拟控制进行求导,因此增大了计算量.文献[12-13]提出一种指令滤波技术,可以直接求出虚拟控制量及其导数,因此可有效降低计算量.文献[14]结合反步控制和指令滤波技术设计控制器,通过仿真验证了指令滤波技术的有效性,但液压系统存在高频干扰,因此很难测量系统的物理量,进而影响系统的跟踪精度.
本文针对电液位置伺服系统的不确定非线性及状态不可测问题,提出一种基于指令滤波的输出反馈控制策略.通过设计扩张状态观测器,对系统状态及外干扰进行估计,克服状态的不可测问题,同时补偿时变干扰对控制性能的影响.利用指令滤波技术解决反步计算中的微分爆炸问题,同时保证较好的跟踪效果.通过对比实验证明了所设计控制器的有效性.
1 系统建模与问题描述
电液位置伺服系统示意图如图1所示,其动力学方程为
(1)
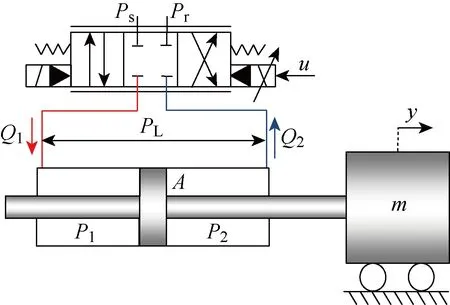
Ps—供油压力,Pr—回油压力,u—控制输入Q1,Q2—液压缸左,右腔流量,m—负载质量图1 电液伺服系统示意图Fig.1 Electro-hydraulic servo system schematic

忽略液压缸的外泄漏,则液压缸的压力动态方程为
(2)
式中:βe为体积弹性模量;Vt为系统控制腔总容积;Ct为内泄漏系数;QL为负载流量;Q(t)为建模误差.
对于电液伺服阀,阀芯位移(xv)与控制输入(u)的关系为xv=kiu,ki为正常数,因此电液伺服阀流量方程为
(3)

(4)
则整个系统可由如下状态方程表示:
(5)
f=-Bx2/m
q(t)=4βeAQ(t)/(Vtm)
对液压系统有以下合理假设:
假设1系统位置指令x1d∈C3(有界区间)并且有界,电液伺服系统在实际工作中满足0 假设2干扰项q(t)和d(t)有界,即 |q(t)|≤M, |d(t)|≤N (6) 式中:M,N为未知正常数. 假设3函数g(u,x3)相对于x3为Lipschitz,φ(x2,x3)相对于x2,x3为Lipschitz,f(x2) 相对于x2为全局Lipschitz. 基于系统模型(5)设计扩张状态观测器(ESO),对系统状态及干扰进行估计[15].定义x4=q(t),系统状态扩展为x=[x1x2x3x4]T.用h(t)表示x4的导数,则模型(5)可以表示为 (7) (8) 式中:ω0为观测器唯一的参数,ω0>0. 扩张状态的估计误差可以表示为 (9) 对于矩阵A,存在一个正定矩阵P满足如下等式: ATP+PA=-I (10) 通过以上设计可以推断观测器是稳定的,且可以通过增大带宽ω0来减小状态的估计误差[10]. (1) 定义误差变量: (11) 式中:z1为位置跟踪误差;z2和z3为滤波前后系统状态误差;x1d为位置期望指令;γi(i=1,2)为指令滤波器的输出虚拟控制量. 为了在反步计算中减小计算量,将标准虚拟控制量α1,α2直接通过指令滤波器输出其虚拟控制量γ1,γ2及导数.指令滤波器的结构如图2所示,图中αi为标准虚拟控制,ζ和ωni分别为滤波器的阻尼及带宽,s为传递函数过程中的物理量. 图2 指令滤波器结构图Fig.2 Command filter structure diagram 指令滤波器的状态空间表达式为 (12) 通过分析指令滤波器的结构及表达式可知,虚拟控制量的导数可以直接获得,获得该导数减小了反步解析计算量.此外,只要选择足够大的ωni就可以保证输入与输出的误差足够小. (2) 定义补偿跟踪误差: (13) 构造标准虚拟控制量为 (14) 结合式(8)和(11)可得 (15) 通过以上分析可得实际控制律为 (16) 式中:k3为反馈增益,k3>0. 选择Lyapunov函数为 (17) 对式(17)进行求导 (18) 根据前面定义的ε2和ε3可知,存在常数c1,c2,c3和c4使得下式成立: (19) 定义 δi=‖PBi‖,i=2,3,4 κ1=k2ω0+c1,κ3=ω0+c3 根据以上分析,式(18)可以表示为 κ2|ε3||v3|+κ3|ε2||v3|+ -W+ζ (20) 其中: Z= λ(Λ)为矩阵Λ的特征值. 定义Λ为 对式(18)进行积分得 (21) 式中:τ=2λmin(Λ)min{1,1/λmax(P)}. 通过以上证明可知,当q(t)≠0,d(t)≠0时,V(t)∈L∞,可证明闭环系统所有信号均有界;当q(t)=0,d(t)=0时,有W∈L2,且W一致连续,根据Barbalat引理可知,随着时间t→∞以及W→∞,控制器可以得到有界渐进跟踪性能,其中L2和L∞代表有界数列空间.以上证明了闭环系统的稳定性,当选择足够大的ωni时可以保证滤波器输入与输出误差足够小,进而保证跟踪误差z1的渐进稳定性,关于z1的稳定性证明可参考文献[12]. 图3 电液位置伺服系统实验平台Fig.3 The experiment platform for electro-hydraulic position servo system 为验证本文所提控制方法的有效性,利用图3所示的平台进行实验.该平台的系统参数为A=9.047×10-4m2,m=30 kg,Ps=12 MPa,kt=1.2×10-8m3/(s·V·Pa0.5),βe=7×108Pa,B=4 000 N·m·s/rad. 为了测试目标控制器的性能表现,选取3种控制器进行交叉对比,将对比结果用最大值Me、平均值μ和标准差σ3个统计量进行表征[10]. 对比控制器如下: (1) 基于指令滤波的输出反馈控制器(CFOFRC),该控制器有效结合了扩张状态观测器,为了方便实验,仅对α1进行滤波,控制器参数k1=1 200,k2=200,k3=35,ωn1=500,ω0=200,ζ=1. (2) 输出反馈控制(OFRC),该控制策略与(1)中设计方法一致,且所选取的控制参数与(1)中参数相同,但该策略未结合指令滤波技术. (3) 前馈PI控制器(VFPI),控制器参数kP=8 000,kI=2 000,kv=35.55 V·s/m. 选取期望指令信号的值为x1d=10 arctan[(1-e-t)sin(πt)]/0.785 4 (mm).图4为控制器位置跟踪误差(δ)对比.通过分析可知,本文所提CFOFRC控制器的跟踪效果优于其他控制器,最后两个跟踪周期的各项性能指标对比见表1. 表1 工况1下性能指标表Tab.1 Performance indices for Case 1 工况2的控制参数与工况1的控制参数相同,选取期望指令信号数值为x1d=10 arctan[(1-e-t)sin(2πt)]/0.785 4 (mm),该工况下指令频率的加大会激发未建模动态,从而影响控制精度.控制器位置跟踪误差如图5所示,最后两个跟踪周期的各项性能指标如表2所示. 图5 工况2 控制器跟踪误差对比图Fig.5 The controller tracking error comparison for Case 2 表2 工况2下性能指标表Tab.2 Performance indices for Case 2 由此可见,在频率加大的情况下,CFOFRC的控制效果仍然优于其他控制器,进一步验证了所提控制方法的有效性. 针对电液伺服系统模型中存在不匹配的不确定非线性和状态不可测的问题,提出一种基于指令滤波的输出反馈控制算法.设计扩张状态观测器对系统状态及时变干扰进行估计,设计指令滤波器减弱反步计算过程中的解析计算量.选择Lyapunov函数证明了系统的全局稳定性.通过对比CFOFRC、OFRC和VFPI 3种控制器,验证了基于指令滤波的输出反馈控制方法可以有效解决状态不可测问题,同时可以降低强干扰对跟踪性能的影响及反步中解析计算量.实验结果验证了方法的有效性.2 控制器的设计
2.1 ESO设计
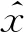
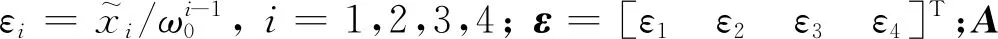
2.2 指令滤波反步控制器设计

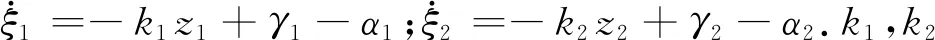
3 稳定性证明

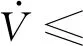
[|v1| |v2| |v3| |ε1| |ε2| |ε3| |ε4|]T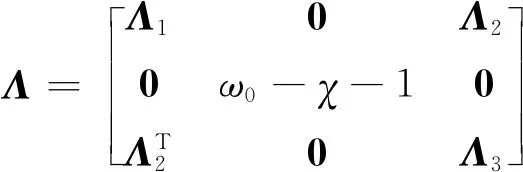

4 实验结果及分析
4.1 工况1

4.2 工况2
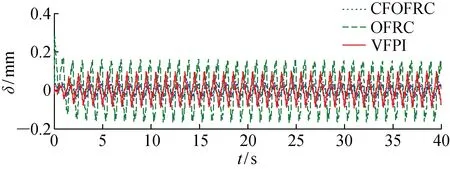
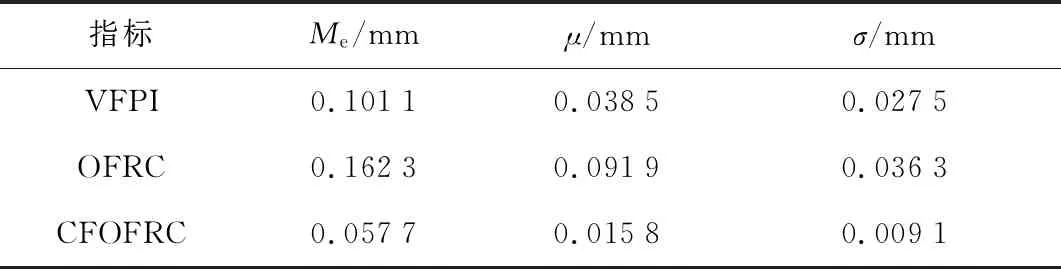
5 结语
